差分拉曼光谱对眼药水塑料瓶的分类研究

陈丽萍，唐宇璇，姜红，王圆圆，章欣，段斌，刘峰

差分拉曼光谱对眼药水塑料瓶的分类研究

陈丽萍1，唐宇璇1，姜红1，王圆圆1，章欣2，段斌2，刘峰2

（1.中国人民公安大学 侦查学院，北京 100038；2.南京简智仪器设备有限公司，南京 210049）

建立一种便捷精准无损检验眼药水塑料瓶的方法。使用便携式差分拉曼光谱仪检测33个塑料眼药水瓶，根据获得的各样品数据，包括差分拉曼光谱图的峰位、峰数等对样品进行成分分析，并通过统计分析软件“统计产品与服务解决方案”（SPSS 26.0）对样品进行均值聚类，利用轮廓系数优选值。对分类结果中样品数目较多的一类样品进行填料分析，利用皮尔逊相关系数验证分析结果的准确性。样品主要成分为聚乙烯和聚对苯二甲酸乙二醇酯，利用轮廓系数优选值为2，均值聚类算法对样品的分类结果与成分分析结果能够相互印证。以聚乙烯类样品为例，根据填料不同可将其分为7组。皮尔逊相关系数计算结果能够证明上述分类分组结果可靠。利用该方法能够准确无损地检测眼药水塑料瓶，并对其进行分类研究。

差分拉曼；眼药水瓶；均值聚类；相关性分析；轮廓系数

近年来，与眼药水相关的案件时有发生，眼药水瓶常出现在各类案件现场，对其进行检验可为公安机关侦查工作提供帮助。眼药水瓶多为塑料制品，现阶段已有大量检测塑料的方法，例如拉曼光谱法[1]、红外光谱法[2]、液相色谱/质谱法[3-4]、气相色谱法[5]以及扫描电镜/能谱法[6]等。在上述方法中，一些操作复杂、所需时间长，部分方法存在易受干扰的问题，还有一些方法的使用会损坏检材。差分拉曼光谱法具有较多优点，如操作简单、便捷，抗噪声、干扰性强，无损检材等[7-8]，故选用便携式差分拉曼仪对所收集的眼药水塑料瓶进行检测分析。

1 实验

1.1 实验原理

差分拉曼技术[9]原理见图1，其利用有细微偏移的不同波长的激发光测得2张不同的拉曼光谱，理论上将光谱的基线对齐后，两条谱线相减，使噪声背景和受激发射谱彻底抵消，最后再通过去噪解卷积算法获得更纯净的拉曼光谱[10]。

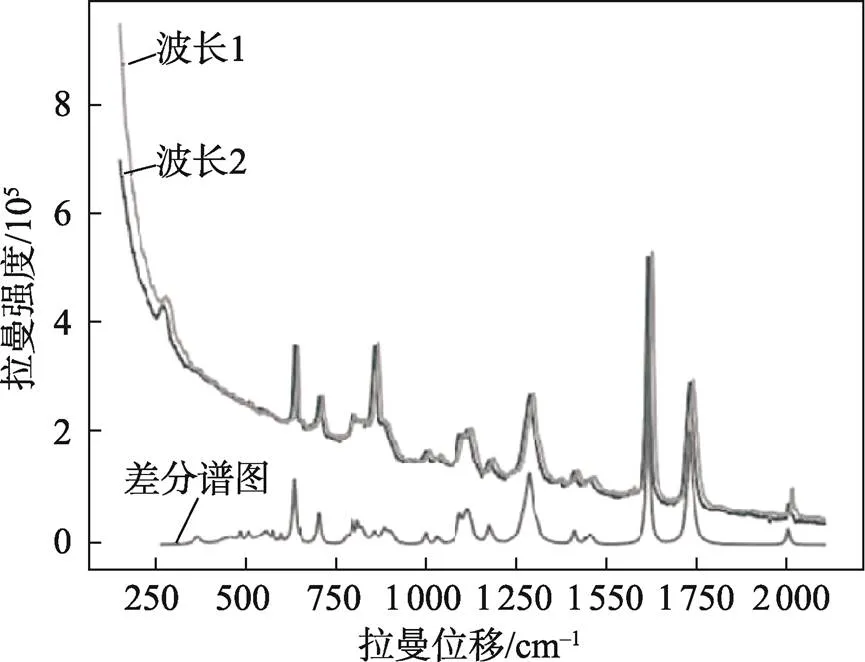
图1 差分拉曼原理解释示意图

1.2 原材料

选择了市面常见的33个不同品牌不同厂家的眼药水塑料瓶样品（样品表略）。各样品包括透明与不透明眼药水塑料瓶，其中透明样品包括无色、红色、蓝色、棕色样品，不透明样品为白色。

1.3 设备及仪器

主要仪器：SERDS Portable–Standard 型便携式差分拉曼光谱仪，南京简智仪器设备有限公司。

1.4 实验过程

1.4.1 实验条件

实验条件：激发光源波长为785 nm和784 nm，激光功率为440 mW，测试波数范围为260～2 800 cm−1，积分时间为10 s，分辨率为5 cm−1。

1.4.2 样品前处理

用乙醇棉球对33个样品进行擦拭，样品晾干后贴上编号待检。

1.4.3 样品检测方法

电脑设置相关参数，将样品按序置于差分拉曼光谱仪激光探头前，在自然光环境下完成检测。

1.4.4 重现性实验

为保证实验仪器的稳定性，随机选取样品17#，设置上述实验条件，对样品17#的同一部位进行5次平行检测。

2 结果与分析

2.1 重现性实验结果

重现性实验结果表明（见图2），5次平行实验在1 059、1 125、1 292、1 437、2 006 cm−1都存在明显的特征峰，而且峰数、峰位、峰强都基本一致，由此判断实验仪器稳定。

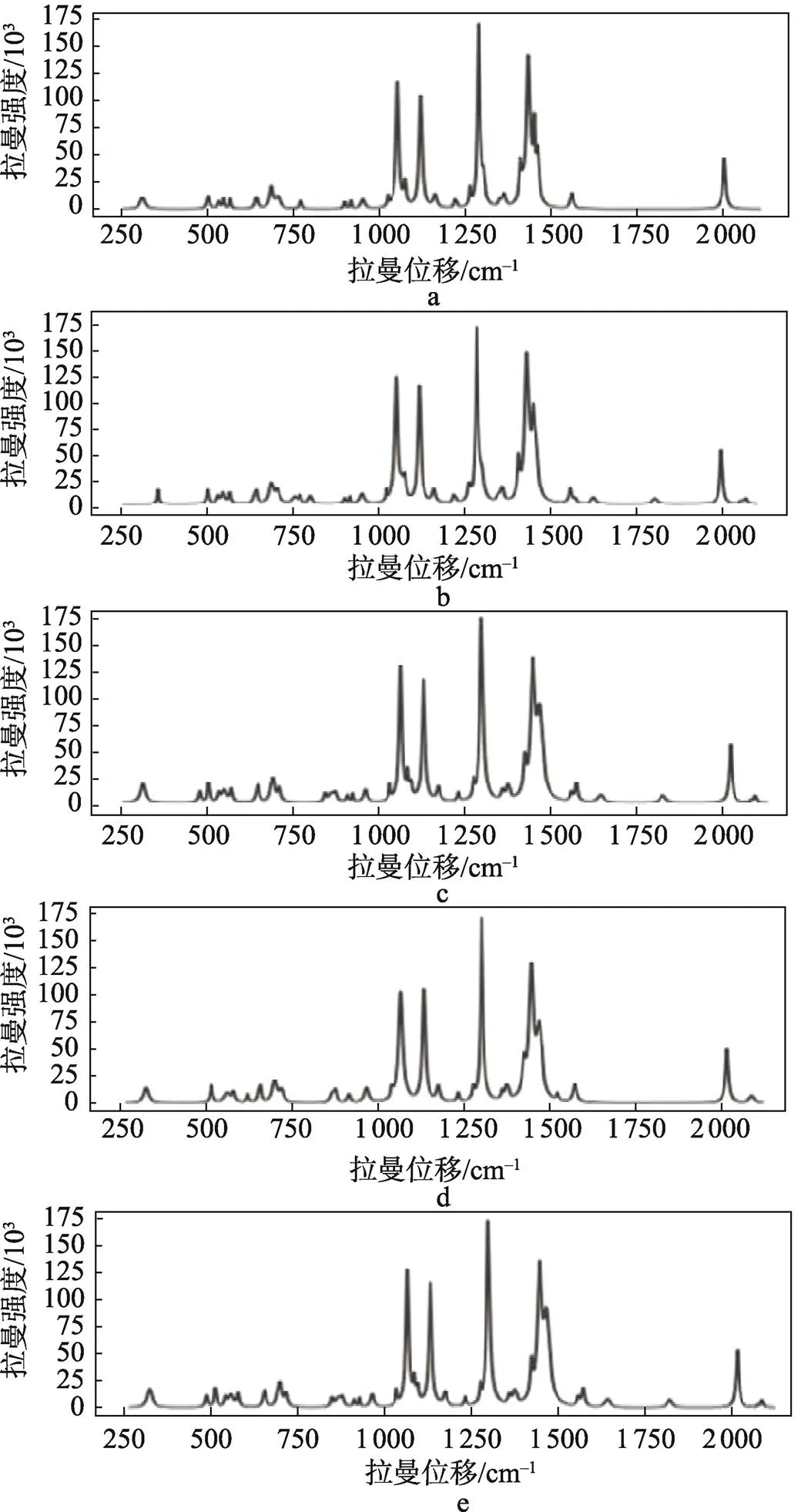
图2 重现性实验结果

2.2 成分分析

眼药水塑料瓶主要成分有聚对苯二甲酸乙二醇酯（PET）、聚乙烯（PE）、聚丙烯（PP）。通过查阅文献获得目前已知塑料成分的主要拉曼特征峰，将各成分的相同特征峰以及不在扫描范围的特征峰去除，留下每个成分特有的特征峰。分析实验所得每个样品的差分拉曼光谱图，判断在误差范围内每个样品是否存在拉曼特征峰与各塑料成分特有的拉曼特征峰重合，若存在，则判断该样品含对应塑料成分。分析表1可知，有18个样品的主要成分为聚乙烯（PE），另15个样品的主要成分为聚对苯二甲酸乙二醇酯（PET）。

表1 样品成分分析结果

Tab.1 Sample composition analysis results

PE类的主要拉曼特征峰[11]在1 063、1 129、1 295、1 440、2 721、2 848、2 882 cm–1处（见图3）。选择25号样品（见图4），通过比较分析发现，其在1 059、1 125、1 292、1 439 cm–1处存在拉曼特征峰，故可认定25号样品主要成分为PE。

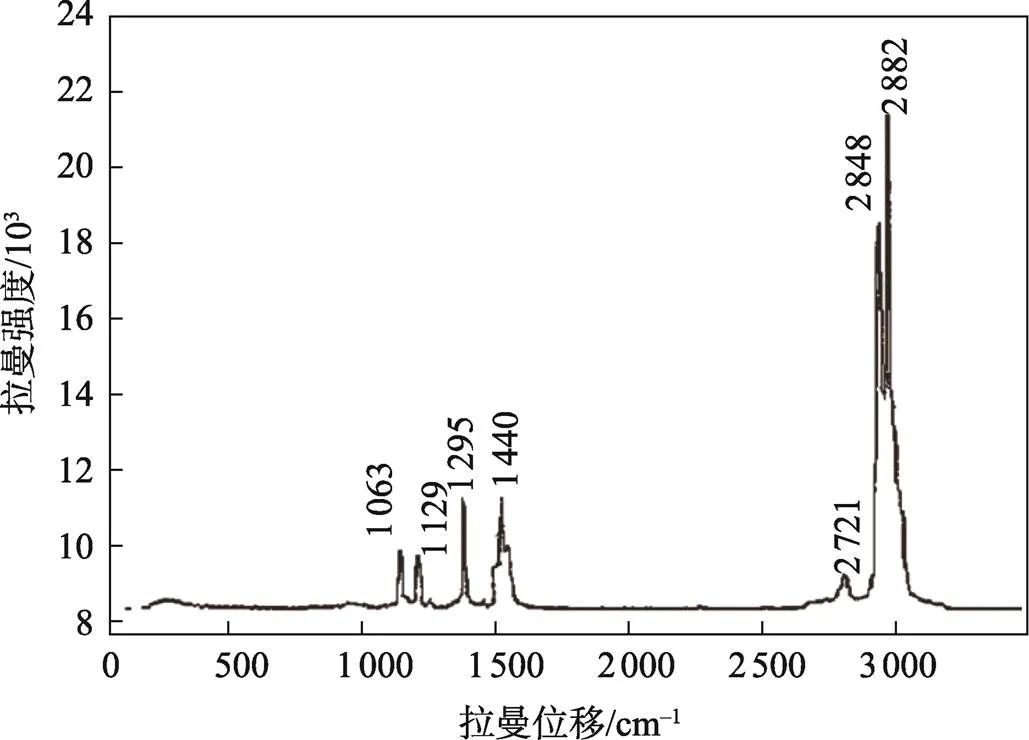
图3 PE的标准拉曼光谱图

PET类的主要特征拉曼峰[12]分别在632、858、1 096、1 289、1 614、1 727 cm−1处（见图5），选择9号样品（见图6），通过比较分析发现，其在629、855、1 093、1 287 cm−1处存在拉曼特征峰，故可认定9号样品的主要成分为PET。

2.3 优选K值进行K均值聚类分析

为使分类结果更加科学准确，减小人工分类误差，利用均值聚类分析验证上述结果。均值聚类算法通过距离评定相似性，2个对象距离越近则相似程度越大，距离接近的对象组成簇，再根据数据变量与聚类中心的相似度迭代更新聚类中心位置，以此减小类簇的误差平方和，直到其不再改变或目标函数收敛，分类停止[13]。在该方法中，最优初始值的选取尤为重要。

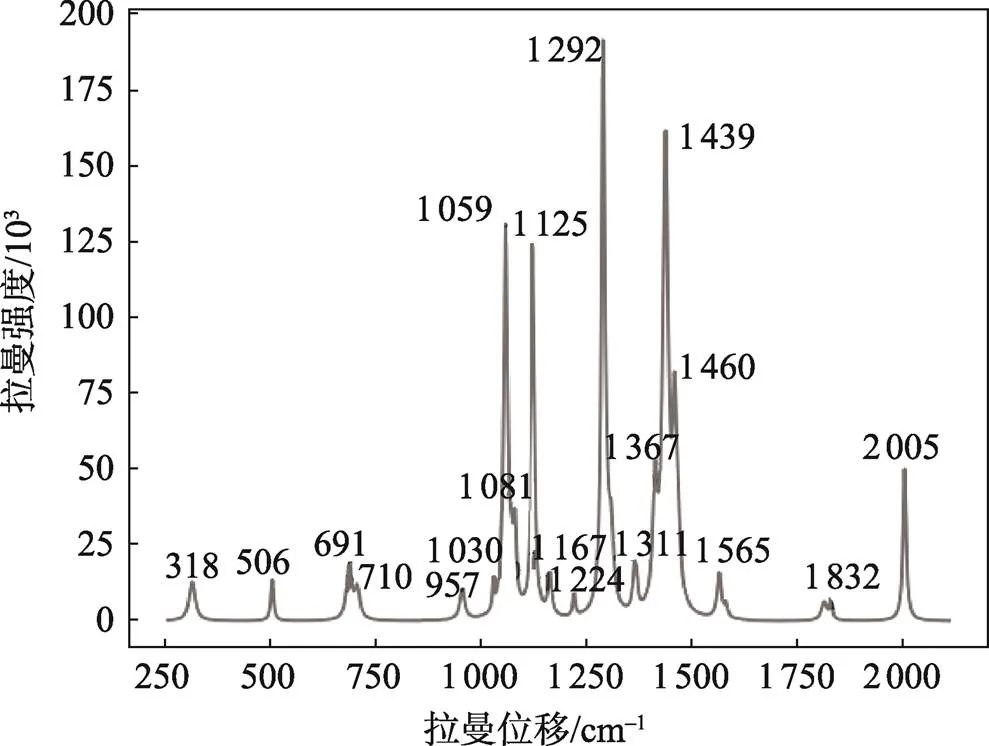
图4 样品25#的差分拉曼光谱图

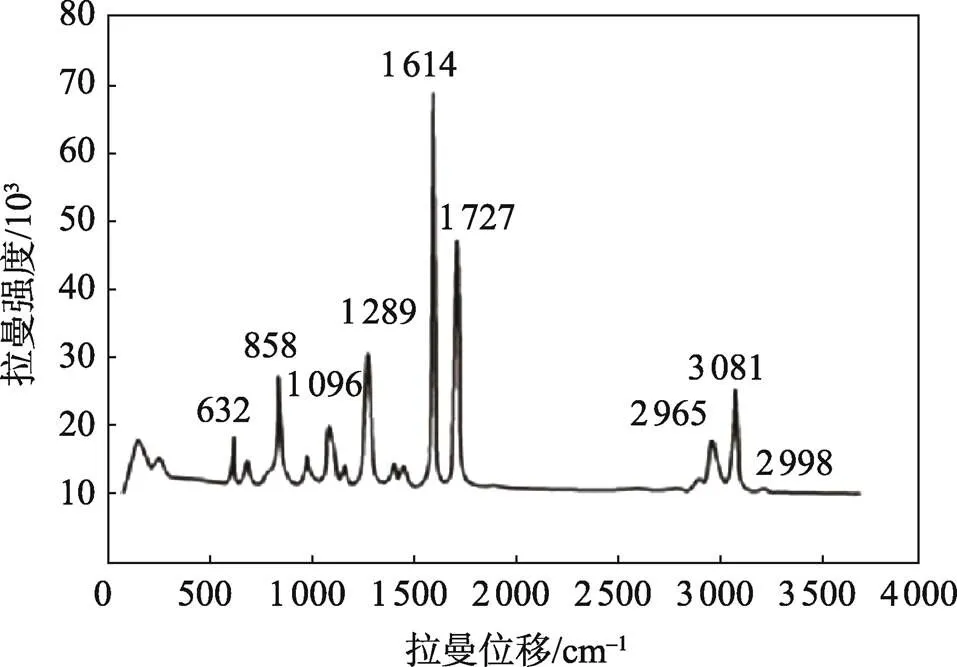
图5 PET的标准拉曼光谱图

图6 样品9#的差分拉曼光谱图

轮廓系数[14]（Silhouette Coefficient）是结合内聚度和分离度2种因素来评估聚类效果的方式，其计算方法如下：

1）计算样品到同簇中其他样品的距离的平均值()。

2）令样品到某一不包含它的簇C内的每个点的平均距离为b，计算() =min{b1,b2, ...,b}。

3）距离即指不相似度，距离越大，不相似度越大。()是样品到同簇内其他样品不相似程度的平均值，()越小，说明该样品与同簇其他样品越相似，越应该被聚类到该簇。()是样品到其他簇的平均不相似度的最小值，()越大，说明该样品与其他簇不相似度越大，越不属于其他簇。

4）根据()和()定义样品的轮廓系数()：

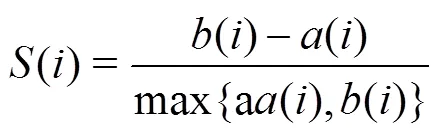
由此可见，()取值在[−1,1]，该值越大，说明对样品的聚类越合理。将各样品的轮廓系数求均值，即为聚类结果的轮廓系数，能够用于度量该聚类是否合理有效。故在进行均值聚类分析之前，分别计算不同值所得聚类结果的轮廓系数，轮廓系数最大时所对应的值即为最优聚类值。

实验中利用数学软件Matlab计算不同值时每个样品的轮廓值，得到如图7所示结果。通过软件数据游标功能读取各个样品的对应轮廓值，再计算出平均值，从而得出该值对应聚类结果的轮廓系数。

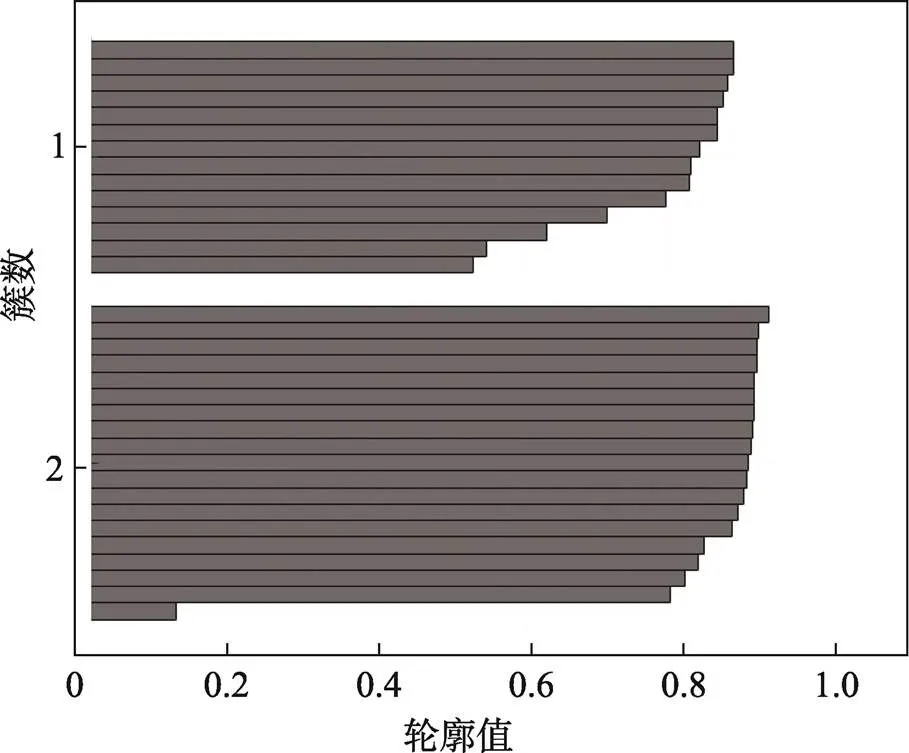
图7 K值为2时聚类结果轮廓图

其中，当为7时，出现较多样本轮廓值为负且分布较分散（见图8），说明聚类数过多，故停止计算。

为2、3、4、5、6时，计算结果见表2。由表2可知，为2时，轮廓系数最大，聚类效果最好。

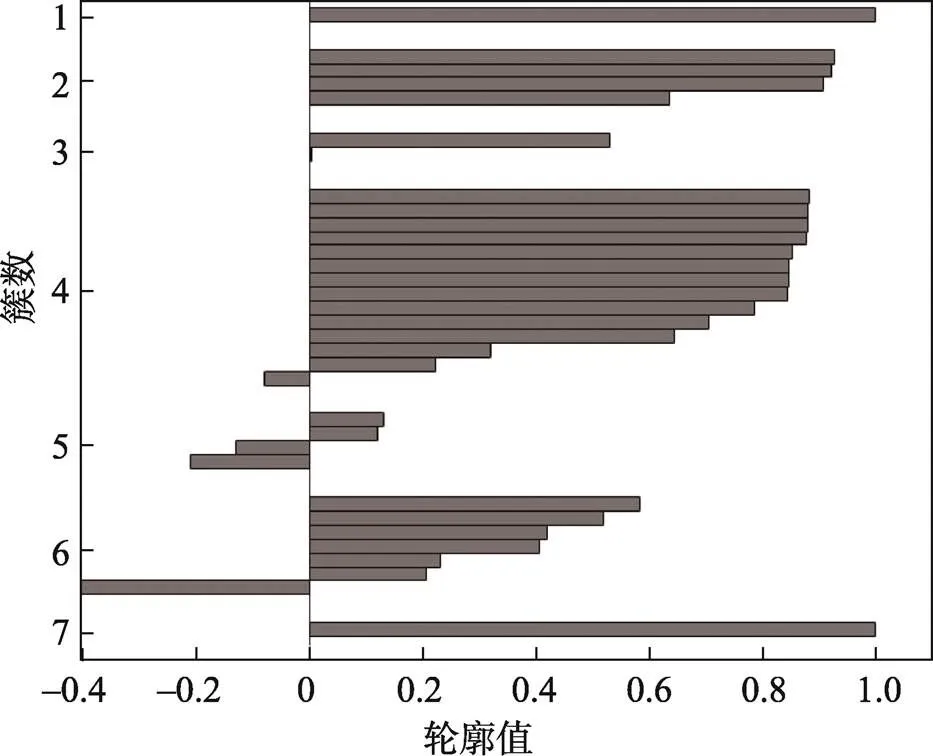
图8 K值为7时聚类结果轮廓图

表2 轮廓系数计算结果

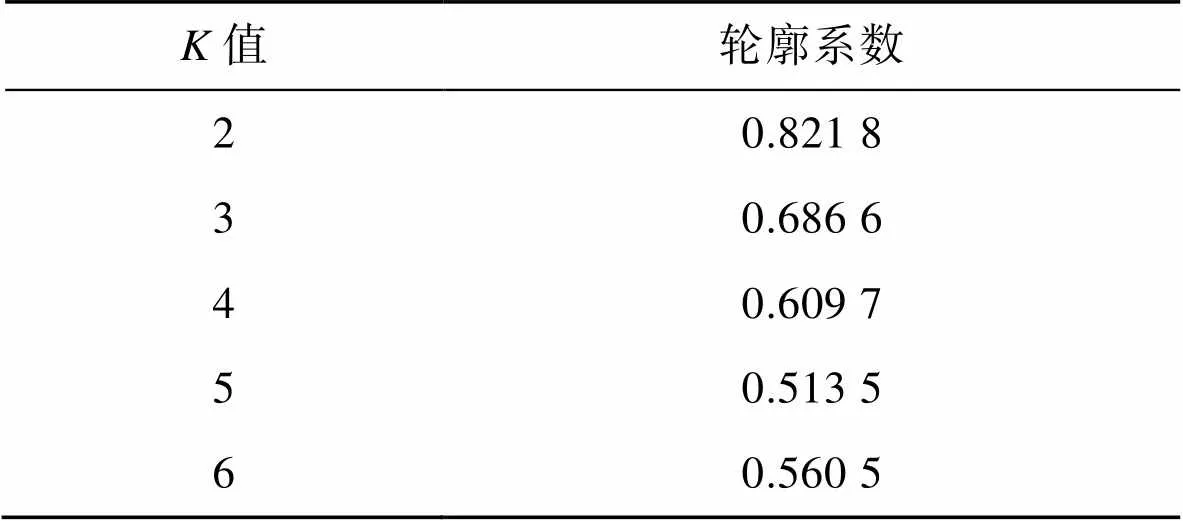
Tab.2 Calculation results of Silhouette Coefficient

根据上述结果，将值设置为2，对样品进行均值聚类分析得到聚类结果（见表3），并与表1中结果相比较，发现只有26号样品分类结果不同，故在误差允许范围内，能够认为表1中分类结果可靠。

表3均值聚类分析结果

Tab.3 K-means clustering results

2.4 填料分析

塑料中常见的填料有碳酸钙、高岭土、硫酸钡等，填料的差异也是导致样品主要特征峰不同的原因之一，故通过查找文献获得常见填料的主要特征峰，将各填料相同的特征峰以及不在扫描范围的特征峰去除，留下各填料特有的特征峰。分析实验所得差分拉曼光谱图，判断在误差范围内（±5 cm−1）样品是否存在拉曼特征峰与各填料特有的拉曼特征峰位置重合，若存在，则判断该样品含对应填料。以样品数目较多的第Ⅰ类为例，分析结果见表4。

每组样品数目较少，可以不必再进一步分类。若实际操作中样品数目过多，可使用X射线荧光光谱法[15]测样品中所含无机元素种类及含量，以便对样品做出再区分。

表4 第Ⅰ类的填料分析结果

Tab.4 Analysis results of type I filler

二氧化钛的主要拉曼特征峰在449、612 cm−1处[16]，分析实验所得样品4#光谱图（见图9），发现样品具有特征峰分布在452 cm−1处和613 cm−1处，故可以判断样品4#中存在填料二氧化钛。

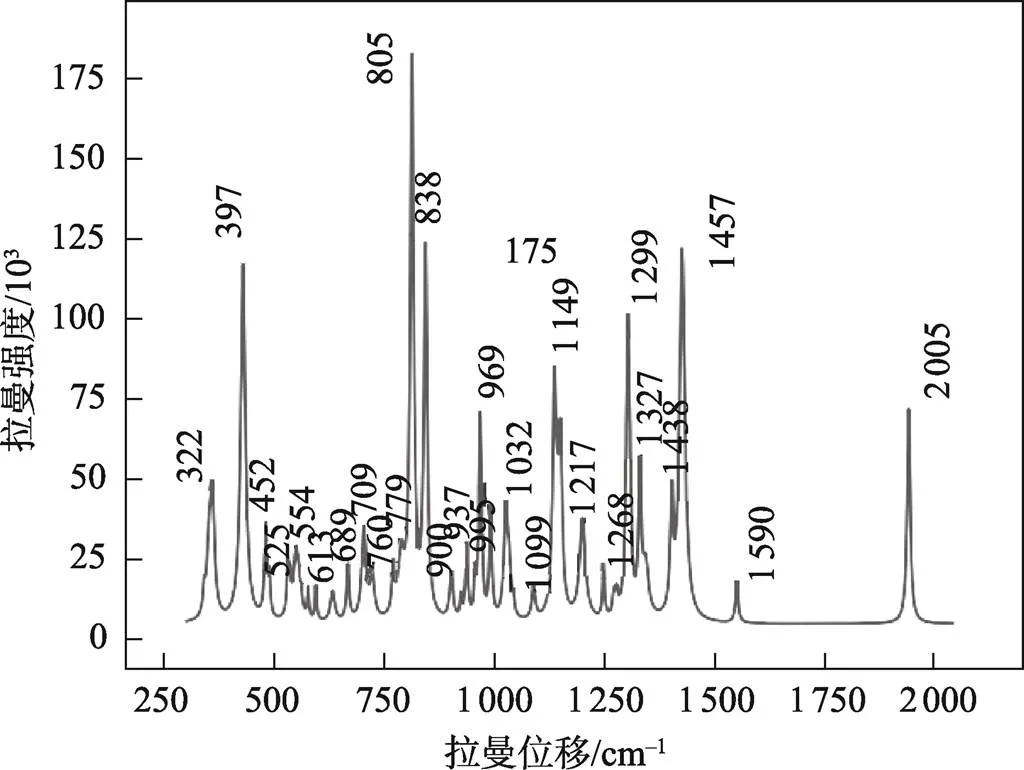
图9 样品4#的差分拉曼光谱图

碳酸钙在208、711、1 085 cm−1处有主要拉曼特征峰[16]，分析实验所得样品8#的光谱图（见图10），可以发现样品具有特征峰分布在710 cm−1处和1 080 cm−1处，故可以判断样品8#中存在填料碳酸钙。

纤维素在371、1 114、1 285、1 330、1 371、1 462 cm−1处有主要拉曼特征峰[17]，分析实验所得样品30#光谱图（见图11），发现样品具有特征峰分布在363、1 292、1 462 cm−1处，故可以判断样品30#中存在填料碳酸钙。

从样品24#的差分拉曼光谱图（见图12）中发现样品具有的特征峰分布在451、611 cm−1处，故可以判断样品24#中存在填料二氧化钛；样品具有的特征峰分布在709、1 080 cm−1处，故可以判断样品24#中存在填料碳酸钙；样品具有的特征峰分布在1 292、1 369、1 459 cm−1处，故可以判断样品24#中存在填料纤维素。

图10 样品8#的差分拉曼光谱图

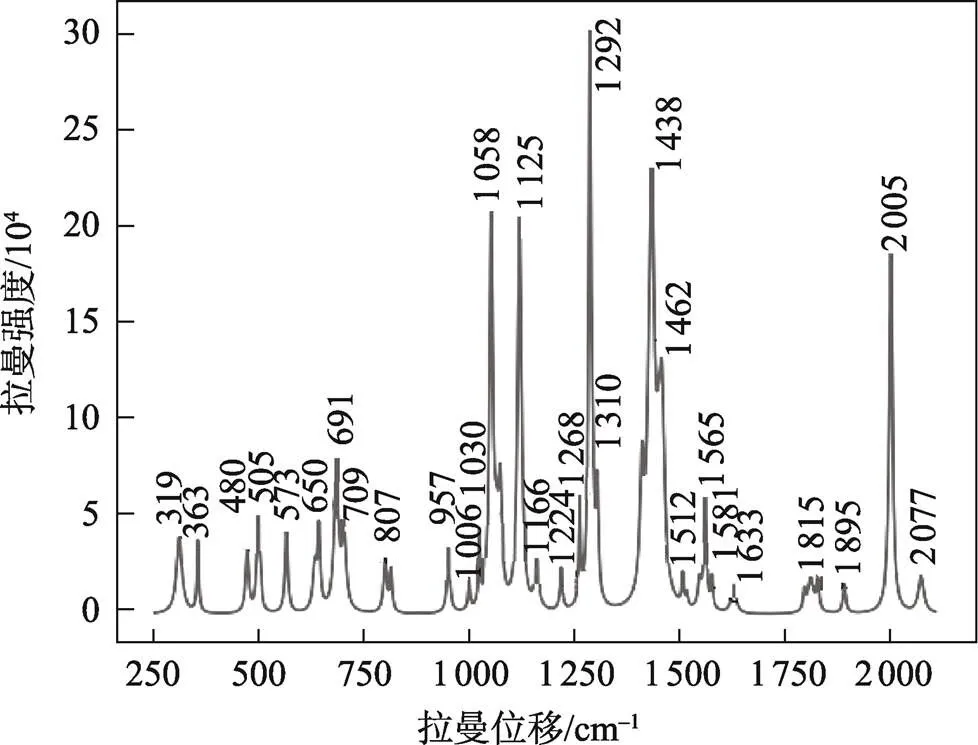
图11 样品30#的差分拉曼光谱图

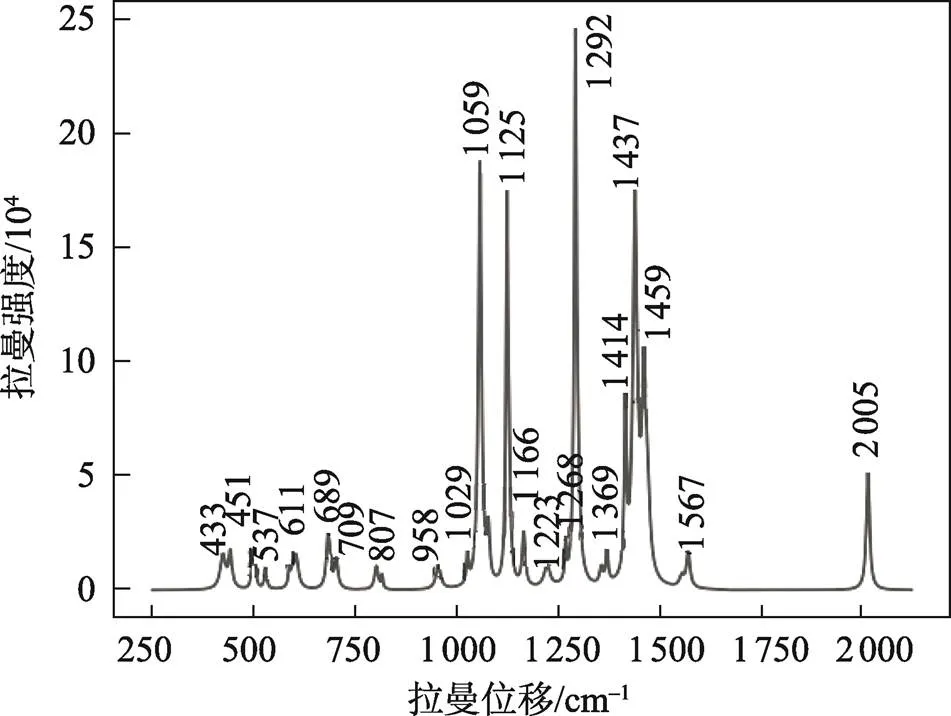
图12 24#样品的差分拉曼光谱图

2.5 皮尔逊相关系数

Pearson相关系数[18-19]是值介于−1与1之间，用来度量2个变量之间的线性相关关系的数学量，其定义：

计算各样品之间皮尔逊相关系数，可根据相关性判断分类结果是否可靠。选取样品1#、2#、17#、25#、10#、32#、33#，计算此7个样品之间的相关性，结果见表5。

由表5可知，样品1#、2#的相关性大于0.9，样品17#、25#、10#、32#、33#之间的相关性大于0.15，但样品1#、2#与样品17#、25#、10#、32#、33#之间相关性均小于0.12且多为负数，显著不相关；与表1中样品1#、2#为一类，样品17#、25#、10#、32#、33#为一类的成分分析相符，可认为表1所示分类结果可靠。样品10#、32#、33#之间的相关性都大于0.96，样品17#、25#的相关性为0.985，但样品10#、32#、33#与样品17#、25#之间的相关性都小于0.212；与表4中样品17#、25#为一组，样品10#、32#、33#为一组的填料分析结果相符，可认为表4所示分组结果可靠。

表5 皮尔逊相关性分析结果

Tab.5 Pearson correlation analysis results

3 结语

1）文中利用便携式差分拉曼光谱仪对收集的33个塑料眼药水瓶进行检测，得到差分拉曼光谱图以及相关数据。对样品进行成分分析，样品可分为PE和PET 2类，利用Matlab计算不同聚类数时分类结果的轮廓系数，优选出最佳聚类数为2，利用均值聚类法使值为2，对分类结果进行验证，结果可靠。对PE类样品进行填料分析，可将其分为7组，每组样品数量较少，可不必再分类。选取7个样品进行皮尔逊相关系数分析，通过比较相关性，可证明上述分类分组结果可靠。

2）该方法理论和操作方法简单，无损样本，实验数据有效准确，能对相关案件的物证分析提供思路，对公安侦查工作提供帮助。

3）后续还能够使用X射线荧光光谱法测样品中所含无机元素种类及含量，结合文中内容，对此类药品塑料包装材料进行更精确的分析。

[1] DENG Ji-hong, JIANG Hui, CHEN Quan-sheng. Determination of Aflatoxin B(1) (AFB(1)) in Maize Based on a Portable Raman Spectroscopy System and Multivariate Analysis[J]. Spectrochimica Acta Part A, Molecular and Biomolecular Spectroscopy, 2022, 275: 121148.

[2] ZHANG Xin, GAO Zhang-ming, YANG Ying-lin, et al. Rapid Identification of the Storage Age of Dried Tangerine Peel Using a Hand-Held Near Infrared Spectrometer and Machine Learning[J]. Journal of Near Infrared Spectroscopy, 2022, 30(1): 31-39.

[3] ANSAR S M, JIANG Wen-lei, MUDALIGE T. Analysis of Verteporfin Liposomal Formulations for Phospholipids and Phospholipid Degradation Products by Liquid Chromatography-Mass Spectrometry (LC-MS)[J]. Journal of Pharmaceutical and Biomedical Analysis, 2022, 208: 114473.

[4] Pablo R, Cortina, Ramón A, et al. Determination of Volatile Organic Compounds in Andean Tomato Landraces by Headspace Solid Phase Microextraction-Gas Chromatography-Mass Spectrometry[J]. Journal of the Brazilian Chemical Society, 2016, 28(1): 30-41.

[5] GARCÍA I V, RODRÍGUEZ B Q A, PASEIRO L P, et al. Identification of Intentionally and Non-Intentionally Added Substances in Plastic Packaging Materials and Their Migration into Food Products[J]. Analytical and Bioanalytical Chemistry, 2018, 410(16): 3789-3803.

[6] 务瑞杰, 姜红. 扫描电镜/能谱法检验塑料拖鞋[J]. 上海塑料, 2017(1): 18-22.

WU Rui-jie, JIANG Hong. A Study on Discrimination of Plastic Slipper by SEM/EDS[J]. Shanghai Plastics, 2017(1): 18-22.

[7] 方刚, 殷磊, 刘峰, 等. 基于差分喇曼技术在抑制荧光中的应用研究[J]. 激光技术, 2019, 43(3): 359-362.

FANG Gang, YIN Lei, LIU Feng, et al. Application Research of Fluorescence Suppression Based on Differential Raman Technique[J]. Laser Technology, 2019, 43(3): 359-362.

[8] 姜红, 朱晓晗, 何歆沂, 等. 差分拉曼光谱法对塑料瓶的鉴别分析[J]. 中国测试, 2020, 46(8): 76-79.

JIANG Hong, ZHU Xiao-han, HE Xin-yi, et al. Differential Raman Analysis of Plastic Bottles[J]. China Measurement & Testing Technology, 2020, 46(8): 76-79.

[9] LIEBER C A, MAHADEVAN-JANSEN A. Automated Method for Subtraction of Fluorescence from Biological Raman Spectra[J]. Applied Spectroscopy, 2003, 57(11): 1363-1367.

[10] 李晟全, 姜红, 常鹏宇, 等. 差分拉曼光谱结合聚类分析对塑料牙刷柄的检验研究[J]. 化学研究与应用, 2021, 33(6): 1174-1180.

LI Sheng-quan, JIANG Hong, CHANG Peng-yu, et al. Study on the Inspection of Plastic Toothbrush Handle by Differential Raman Spectroscopy and Cluster Analysis[J]. Chemical Research and Application, 2021, 33(6): 1174-1180.

[11] 董鹍, 饶之帆, 杨晓云, 等. 几种塑料的拉曼光谱检测[J]. 塑料工业, 2011, 39(6): 67-70.

DONG Kun, RAO Zhi-fan, YANG Xiao-yun, et al. Determination of Several Plastic by Raman Spectroscopy[J]. China Plastics Industry, 2011, 39(6): 67-70.

[12] 张愚若, 姜红, 刘奎江, 等. 食品塑料包装袋的拉曼光谱分析[J]. 上海塑料, 2020(1): 30-34.

ZHANG Yu-ruo, JIANG Hong, LIU Kui-jiang, et al. Raman Spectroscopy Analysis of Food Plastic Packing Bags[J]. Shanghai Plastics, 2020(1): 30-34.

[13] ZHU Ai-lin, HUA Ze-xi, SHI Yu, et al. An Improved K-Means Algorithm Based on Evidence Distance[J]. Entropy (Basel, Switzerland), 2021, 23(11): 1550.

[14] Kumar Y D, Yadav V, Shukla R. An Efficient Collaborative Recommender System for Textbooks Using Silhouette Index and K-Means Clustering Technique[J]. International Journal of Advanced Intelligence Paradigms, 2019, 1(1): 1.

[15] 刘亚昌, 孙玉友, 张冀峰, 等. 使用手持式X射线荧光光谱仪临场检测爆炸装置塑料碎片[J]. 刑事技术, 2019, 44(3): 228-232.

LIU Ya-chang, SUN Yu-you, ZHANG Ji-feng, et al. Applying Portable X-Ray Fluorescent Spectrometer to Rapidly Detect the Plastic Components from Improvised Explosive Devices[J]. Forensic Science and Technology, 2019, 44(3): 228-232.

[16] 姜红, 田陆川, 王艺霖, 等. 差分拉曼光谱法结合聚类分析检验食品塑料包装盒[J]. 包装工程, 2021, 42(15): 85-93.

JIANG Hong, TIAN Lu-chuan, WANG Yi-lin, et al. Differential Raman Spectroscopy Combined with Cluster Analysis for Inspection of Food Plastic Packaging Box[J]. Packaging Engineering, 2021, 42(15): 85-93.

[17] 刘津彤, 张岚泽, 姜红, 等. 差分拉曼光谱结合支持向量机模型对便签纸的鉴别分析[J]. 化学通报, 2022, 85(2): 259-263.

LIU Jin-tong, ZHANG Lan-ze, JIANG Hong, et al. Identification of Note Paper by Differential Raman Spectroscopy Based on Support Vector Machine[J]. Chemistry, 2022, 85(2): 259-263.

[18] RAHMAN M, CHEN Ning-sheng, MAHMUD G I, et al. Flooding and Its Relationship with Land Cover Change, Population Growth, and Road Density[J]. Geoscience Frontiers, 2021, 12(6): 22-41.

[19] Robert W E. Causation and Pearson's Correlation Coefficient[J]. Journal of Visual Impairment & Blindness, 2015, 109(3): 242-244.

Classification of Plastic Bottles of Eye Drops by Differential Raman Spectroscopy

CHEN Li-ping1, TANG Yu-xuan1, JIANG Hong1, WANG Yuan-yuan1,ZHANG Xin2, DUAN Bin2, LIU Feng2

(1. Investigation Institute, People's Public Security University of China, Beijing 100038, China; 2. Nanjing Jianzhi Instrument and Equipment Co., Ltd., Nanjing 210049, China)

The work aims to establish a rapid, accurate and nondestructive method for testing the plastic bottles of eye drops. Portable differential Raman spectrometer was used to test 33 plastic bottles of eye drops. Then, according to the sample data obtained such as peak position and peak number of the differential Raman spectrum, the composition of the samples was analyzed. At the same time,-means clustering was carried out to the samples by statistical analysis software "Statistical Products and Services Solutions" (SPSS 26.0) and the most optimal-means was selected based on Silhouette Coefficient. The samples with a large number in the classification results were analyzed, and the accuracy of the analysis results was verified by Pearson correlation coefficient. The samples were mainly composed of polyethylene and polyethylene terephthalate. The most optimal-means selected based on Silhouette Coefficient was 2 and the-means clustering algorithm verified the classification result and composition analysis result of the samples. With polyethylene samples as an example, they could be divided into 7 groups according to different fillers. The calculation results of Pearson correlation coefficient proved the reliability of the above classification and grouping results.This method can accurately and non-destructively detect and classify the plastic bottles of eye drops.

differential Raman; bottles of eye drops; K-means clustering; correlation analysis; Silhouette Coefficient

TB99

A

1001-3563(2023)05-0196-07

10.19554/j.cnki.1001-3563.2023.05.025

2022−04−13

国家重点研发项目（2018YFC1602701）；中央高校基本科研业务费专项资金资助（2019JKF418）

陈丽萍（2001—），女，本科生，主攻刑事科学技术理化检验。

姜红（1963—），女，教授，硕导，主要研究方向为理化物证检验的教学。

责任编辑：曾钰婵