一种结构光组合编码模式和解码算法
2023-03-14汪维刚王泽民赵选
汪维刚,王泽民,赵选
(西安工业大学电子信息工程学院,西安 710021)
0 引言
结构光法作为非接触式三维测量技术的一个重要分支,具有测量速度快、成本低、鲁棒性好等优势。按编码方式的不同,编码结构光法可分为直接编码、时间编码和空间编码,文献[1]中概括了时间编码和空间编码主要算法。
随着动态场景下三维测量需求不断增多,有关结构光空间编码的研究也越来越热门。文献[2]设计了一种自均衡伪随机序列,当被测量物体带有多种颜色特征时,无法避免物体自身的颜色对编码图案造成干扰而导致的识别错误。文献[3]提出一种伪随机序列结合相位信息的编码方法,但解码精度会受到编码宽度的影响。文献[4]利用主成分分析和K均值聚类方法设计了一种自适应颜色聚类方法,完成了对颜色强度高低的识别。文献[5]提出利用两种颜色编码的网格条纹模式,但该方法下的网格条纹检测和识别算法均较复杂。
伪随机阵列编码是由伪随机序列通过对角线折叠法或者拼片算法生成,文献[6]中产生大尺寸伪随机阵列的拼片算法较复杂,且码字利用率也较低,随着伪随机阵列尺寸的增大,编码符号也不断增加,增加了后续解码的难度。文献[7]将伪随机序列通过对角线折叠法生成伪随机阵列,但即使在三元域中使用九阶的本原多项式生成伪随机序列,采用对角线折叠法得到的伪随机阵列仍然无法满足高分辨率测量的要求。文献[8]给出了一种三级棋盘的非正式编码,但并没有生成全局唯一的编码图案。
本文设计了一种结构光组合编码模式,将单色正弦条纹和小尺寸伪随机阵列通过不同颜色通道相叠加,得到组合编码图案。单色正弦条纹能够满足高分辨率的测量,且保证了受到被测物体表面颜色干扰的影响更小。相较于大尺寸伪随机阵列,小尺寸的伪随机阵列更容易实现,并且小尺寸伪随机阵列所用码字较少,编码时所需的二值符号种类也更少,降低了后续伪随机阵列的解码难度。所设计的编码图案能够满足动态场景下的高分辨率测量需求。
1 结构光组合编码模式
1.1 基于伪随机序列测量方法分析
伪随机序列具有良好的窗口特性,窗口内的子序列在整个序列中具有全局唯一性。一维伪随机序列可由本原多项式生成,用移位寄存器作为伪随机码产生器,本原多项式及其所指定的反馈移位寄存器共同决定了伪随机序列输出结果。由二元五阶本原多项式所生成的伪随机序列,在大小为5的窗口内的子序列全局唯一。如图1所示。

图1 一维伪随机序列示意图
伪随机阵列通常由一维伪随机序列通过折叠算法或者拼片算法生成,再选取基元符号进行编码,其生成的二维伪随机阵列同样具有窗口特性,即子窗口在整个二维阵列中的全局唯一性。伪随机阵列解码时,通过窗口识别进行特征点检测匹配。由于编码时基元符号需要以领域像素点来表示,多个像素点标识一个基元符号,导致测量分辨率较低。伪随机阵列基元窗口的大小直接影响到编码图案所包含的特征点数,窗口过小会导致解码算法检测基元符号特征点困难,窗口过大会导致空间分辨率低。以一幅大小包含50×50像素点的图像为例,假设编码基元符号大小为10×10像素,如图2所示。

图2 伪随机阵列编码原理图
可以看出,包含50×50像素点的图像,采用以上伪随机阵列编码所得到的特征点仅为25个像素点,严重降低了测量分辨率。为了尽可能地提高测量分辨率,通过减少基元符号的编码像素个数或者采用更大的伪随机阵列模板来获得更多的特征点数。例如,使用更高阶的本原多项式生成长度更长的一维序列来获得更大尺寸的伪随机阵列,再通过多元基元符号进行编码,但即便如此,伪随机阵列编码仍然无法达到高分辨率的测量要求。
1.2 基于相位的测量方法分析
基于相位测量的主要原理是将生成的一系列相移条纹依次按序投射到被测物表面,由于物体高度的调制相位发生变化,通过相位的变化值可以得到被测物体高度信息。N步相移法是指正弦条纹图案的相位值在一个周期内等间距移动N次,即每次移动步长。其中第i幅条纹图像可表示为
式中:Ia(x,y)为环境背景光强,Ib(x,y)为条纹对比度,Δφi为相移步长。通过N幅条纹图案之间的相位差可计算得到包含被测物体高度信息的相位值
由于通过反正切函数得到的相位值是被包裹在[ -π,+π]区间中,需要进行相位展开获取绝对相位φr(x,y),绝对相位和包裹相位的关系可表示为
由于相移法需要投射一系列的相移条纹,因而不适用于动态场景三维测量。其次,由于相移法无法准确获得被测物体的绝对相位值,因此为了保证相位值的唯一性,通常将格雷码与相移法相结合来确保相位的准确性。另外,在空间相位展开过程中,当某一点相位值由于噪声或遮挡发生错误时,该错误会随相位展开路径向后传播,影响相位展开的准确性。
1.3 本文组合编码模式
通过上述分析可知,伪随机阵列编码测量方法能够满足动态三维测量,但空间分辨率较低。基于相位编码的相移法能够提供像素级的高分辨率测量,但由于需要投射多幅条纹图案,因此不适用于动态三维测量。
为了满足动态场景下的高分辨率的三维测量,本文提出了一种组合编码方法。首先,为了满足高分辨率的三维测量,选择基于相位测量的正弦条纹编码;其次,为了能够适用于动态场景三维测量以及保证测量过程中相位值的准确性,选择伪随机阵列对正弦条纹进行再编码。为了减少被测物体表面颜色带来的干扰,使用单色正弦条纹编码。下面将详细论述本文的组合编码原理。
正弦条纹编码中,条纹的周期性无法确保相位值的唯一。为了保证编码图案相位值的唯一性,通常采用格雷码对相位值进行分区定位,但这种方法并不适用于动态场景三维测量。本文选择伪随机阵列对正弦条纹图案再编码,伪随机阵列的窗口特性确保了条纹图案中相位值的全局唯一性,使得正弦条纹编码能够满足高分辨率的动态三维测量。
伪随机阵列的窗口和正弦条纹周期对齐是组合编码方法的核心。本原多项式的阶数决定了伪随机阵列的窗口大小,且窗口大小是固定的,因此从大小来看窗口也具有周期性。由于正弦条纹也具有周期性,因此当窗口大小和正弦条纹编码的周期大小相同时,即可保证在一个窗口中只包含一个完整周期的正弦条纹,单个周期内条纹的相位值唯一,保证了编码图案中相位值的准确。假设正弦条纹的周期为T,窗口宽度大小W,则窗口中是否唯一包含单个完整周期的正弦条纹可表示为
被测物体表面高度变化过快或者表面面型具有复杂曲面会导致局部条纹缺失,如图3和图4所示。

图3 正弦条纹编码图案局部条纹缺失
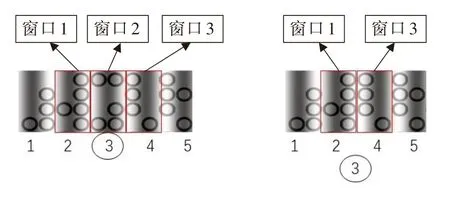
图4 组合编码图案局部条纹缺失
在传统的相移法中,当2号条纹发生缺失,单一相位编码方法无法确定缺失的条纹编号,导致产生的误差会从缺失的2号条纹处开始向后传递直到结束,造成相位值紊乱,致使解码出错。对于本文所设计的组合编码,通过伪随机阵列对正弦条纹进行了再编码,当发生条纹缺失时,通过伪随机阵列窗口特性依然可以保证后续的解码正确性,不会发生误差传递的现象。当被测物表面高度变化过快或者存在断层时发生条纹缺失的情况,当第3号条纹发生缺失,条纹处的伪随机阵列编码也发生缺失。通过伪随机阵列编码的窗口特性,通过窗口1和窗口3可以得出窗口2缺失的信息,从而判断出3号条纹缺失的信息,确保局部条纹的缺失不会影响到后续条纹的解码。
伪随机阵列编码中基元符号的选择至关重要,符号提取和识别与解码效率直接相关。因此,选取的符号应有明显的形状特征,且具备良好的平移、旋转和尺度不变特征。因此,选取圆环作为本文伪随机阵列编码的基元符号。通过Hu矩可以看出,圆环发生变形时Hu矩的七个特征值并没有很大变化,依然能够很好地反映符号特征。

表1 圆环及其变形图案的Hu矩
本文选用二元八阶本原多项式生成长度为255的伪随机序列,按对角线折叠法形成大小为15×17的伪随机阵列,窗口大小为4×2。根据以上算法对大小为1024×768的图像编码,生成的组合编码图案以及截取的部分子窗口图案如图5所示。

图5 空间组合编码图案

表2 编码方法比较
2 组合图案解码算法
组合图案解码算法分为伪随机阵列解码和正弦条纹解码两部分,首先对伪随机阵列图案进行窗口识别匹配,通过窗口定位找到正弦条纹图案中相应窗口位置,对正弦条纹进行傅里叶变换,得到包含物体高度信息的相位值。
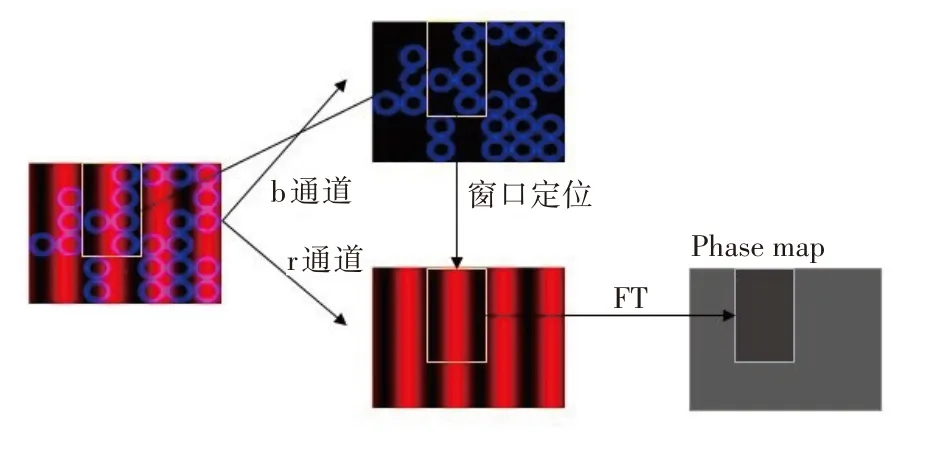
图6 组合图案解码示意图
伪随机阵列解码的本质是对符号特征的提取、识别以及匹配,编码符号良好的平移、旋转和尺度不变特性有利于提高解码效率,图像去噪、滤波等预处理能够使识别匹配更加准确。文献[9]中详细描述了伪随机阵列符号识别匹配过程,其原理如图7所示。

图7 窗口匹配原理
窗口内受到物体高度调制的正弦条纹图像可表示为
其中,a(x,y)为环境背景光强,b(x,y)为条纹对比度,f0为正弦条纹基频,φ(x,y)为被测物体高度信息的调制相位。对其进行傅里叶变换后通过滤波得到基频分量,再进行傅里叶逆变换得到物体调制相位值如下:
通过伪随机阵列图案对正弦条纹图案进行了再编码,伪随机阵列的窗口唯一标识了相位图中的相位值,因此得到的相位无需进行相位展开。
3 实验结果及分析
实验采用的投影仪型号为爱普生(EPSON)CB-2155W,分辨率为1280×800 pixel,工业相机型号为CK U300系列,分辨率为1282×768 pixel。将本文组合图案投射于待测物体表面,通过相机获取受到物体高度调制的变形图案以及局部图案,如图8所示。

图8 采集的变形图案及其局部图案
从图8可以看出,变形图案的伪随机阵列窗口中依然唯一包含单周期正弦条纹,确保了后续解码过程中相位值的准确性。为了方便,截取大小为512×512的局部图案进行计算。将采集的原图案通过颜色通道分离得到伪随机阵列图案和正弦条纹图案,首先对伪随机阵列图案进行解码,通过图案预处理以及符号识别提取,其结果如图9所示。

图9 符号识别结果局部
伪随机阵列完成窗口匹配,通过窗口定位到正弦条纹图案对应窗口中的正弦条纹。前文编码算法确保窗口中只包含一个周期正弦条纹,确保相位值唯一。
通过傅里叶变化求得相位值,如图10所示。其中,图(a)、(c)为传统相移法通过相位展开得到被测平板物体和柱体表面的相位图,图(b)、(d)为本文组合解码算法所得被测平板物体和柱体表面相位图。从图10可以看出,传统相移法中对于噪声等影响产生的噪点,由于相位展开过程中误差累积传播,所得相位图边缘处误差较大。在组合解码算法中,通过伪随机阵列对正弦条纹再编码确保相位值的唯一性,无需进行相位展开,因此相位图中的误差不会影响领域像素点。根据本文算法所得相位图,结合现有标定技术即可完成稠密三维测量。实验证明本文所提组合编码模式和解码算法的有效性,在快速稠密三维测量中具有很大应用前景。

图10 相移法和本文算法所得相位图
4 结语
针对高分辨率的三维测量,提出了一种组合编码模式和解码算法,将伪随机阵列编码和单幅正弦条纹图案组合形成组合编码图案。基于相位测量的正弦条纹编码能够满足高分辨率的三维测量,伪随机阵列编码对正弦条纹进行再编码,使得单幅正弦条纹图案能够适用于动态场景下的三维测量。由于窗口特性确保了测量过程相位值的准确,因此得到的相位值无需再进行相位展开,结合现有的标定技术即可完成高分辨率的动态三维测量。实验结果说明了本文组合编码模式和解码算法的有效性。
