排水孔和防渗墙对导流坝水力坡降和扬压力的影响

郑 禄

(辽宁西北供水有限责任公司，辽宁 沈阳 110000)

在透水地基上建造的水工建筑物，可能会从建筑物底部渗水，承受由上下游水头差异引起的扬压力。上游蓄水越多，渗流越多，对水工结构与地基界面的作用力越大。在新疆，尤其是南疆普遍存在“高地震、高严寒、高海拔、高边坡、深厚覆盖层、多泥沙”的筑坝环境[1]，随着建坝需求变化和筑坝技术发展，一旦坝基防渗处理不合格，后期维修将给运行管理带来极大压力。导流坝及消力池的扬压力分布如图1所示。

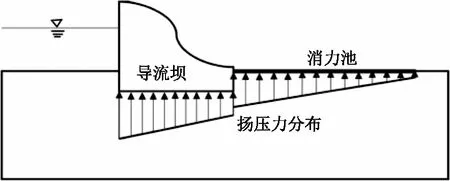
图1 导流坝及消力池的扬压力分布

在这种情况下，扬压力可能会倾覆其周围的水工结构或导致水工结构地板的混凝土表面出现裂缝。渗水易造成水工结构不稳定，这些水工结构的施工需要受到高度重视。因此，应计算施加在整个水工结构和基础上的扬压力以及下游出口的水力梯度。降低扬压力最重要的方法是在上游建造防渗墙，在水工结构下方安装排水渠，在下游安装排水孔。

关于防渗墙和排水孔在减少大坝下方渗流方面的作用，已有少量的研究。例如，麦麦提明·依比布拉[2]为分析某水电站混凝土堆石坝渗流场特性，利用Abaqus有限元软件建立数值模型，研究发现防渗效果与防渗墙深度有关。陈镭[3]探讨了悬索式和封闭式防渗墙的防渗性能，并对厚度、渗透系数等参数进行优化，确定合理的位置分布。游萍等人[4]介绍了在GEO-Seep/W过程中应解决的几个关键问题，并通过数值模拟分析了某边坡在降雨条件下的蓄水条件和水位变化情况下的渗流场变化，对揭示边坡失稳机制有一定的指导作用。周卫国[5]对坝基扬压力及渗流进行了系统地比较分析，结果显示此项措施对坝基扬压力、渗流均有明显的降低。陈博夫等人[6]引入当量长度及附加阻抗概念，分析了帷幕与排水孔的减压效果，发现二者联合作用下的扬压力较防渗帷幕与排水孔单独作用更为精确，更贴近工程实际。

据我们所知，目前在实验室条件下还没有研究过排水孔和防渗墙对土坝下方渗流的同时作用以及对坝体上方扬压力降低的影响。因此本文采用物理和数值模型研究了排水孔和防渗墙对导流坝下水力梯度和扬压力降低的影响，利用Seep/W软件得到了扬压力和水力梯度的分布规律。

1 材料与方法

1.1 实验室模型

在本研究中，实验装置包括一个长150cm、宽10cm、高60cm的立方体容器、100L的供水蓄水池和4kW的泵。实验中所用的多孔介质为天然砂。采用标准普氏实验确定了土壤压实的最佳水分和最佳能量。此外，在使土壤达到最佳压实状态后，通过恒定水头法获得导水率。确定多孔介质的平均粒径为0.55mm、最佳湿度为10.5%、导水率为0.00025m/s。为了使从该水库流入土箱的水流平静下来，在2段之间放置了一个格栅板作为过滤器。上游使用了10、15和20cm的3个水头(h1)，并在渗流池的中部填充厚度为115cm的土壤。

首先，将土壤润湿至最佳值，然后用厚度为10cm的土层填充，使其达到30cm的厚度。这是在标准普氏实验中相同的压实能量和恒定水头法中相同的导水率下进行的。将长30cm、高27cm有机玻璃制成的导流坝模型安装在距中间起点30cm处，使坝基长度等于5cm。下游使用长度为55cm、厚度为1cm的有机玻璃板作为消力池，其上表面与上游地板处于同一水平面，并在消力池中以10cm的间隔嵌入4个直径为1cm的排水孔。

在每个实验中，首先使用螺钉封闭所有排水孔，经过一段时间并稳定渗流后，使用体积为250cm3(±2cm3)的计量容器在下游测量渗流通量。包含渗流池、大坝、消力池护坦、排水孔和防渗墙的物理模型如图2所示。

图2 渗流池、大坝、消力池护坦、排水孔、防渗墙的物理模型

1.2 数值模型

在本研究中，应用GeoStudio软件中的Seep/W模型进行分析。该模型功能强大且全面，用于渗流分析和估计多孔介质中的扬压力和水力梯度。使用拉普拉斯方程用于二维稳定流：

(1)

式中，φ—土壤中的水势；kx和ky—x和y方向上的土壤水力传导率。

φ实际上是压力或孔隙水压力(引起扬压力的原因)和重力势的总和。在均质和各向同性的多孔介质中，假设kx和ky相等。首先在Seep/W软件中绘制多孔介质的几何形状，应用适当的边界条件在左边的垂线以及上游的土壤表面施加一个恒定的电位(上游的水头+土层厚度)。右侧垂线以及消力池表面的边界条件也被认为是恒定电位，等于土层的厚度(即30cm)，其余部分被认为是不透水边界。当排水孔打开时，将其视为渗流点，防渗墙视为不透水界面。为了模拟渗流，用正方形单元对几何形状进行网格划分。采用试错法，根据实验结果对数值模型进行校准后，得到最佳单元数为1441。为了将模拟渗流通量与实验值进行比较，并评估数值模型的效率，使用了相对误差百分比公式：

(2)

式中，Qexp—实验的渗流通量；Qsim—模拟的渗流通量。

2 结果与讨论

2.1 排水孔

2.1.1渗流

为了评估数值模型的效率，以确保精确估算大坝下方不同位置的扬压力和水力梯度，将渗流通量的实验值与模拟值进行了比较，如图2所示。

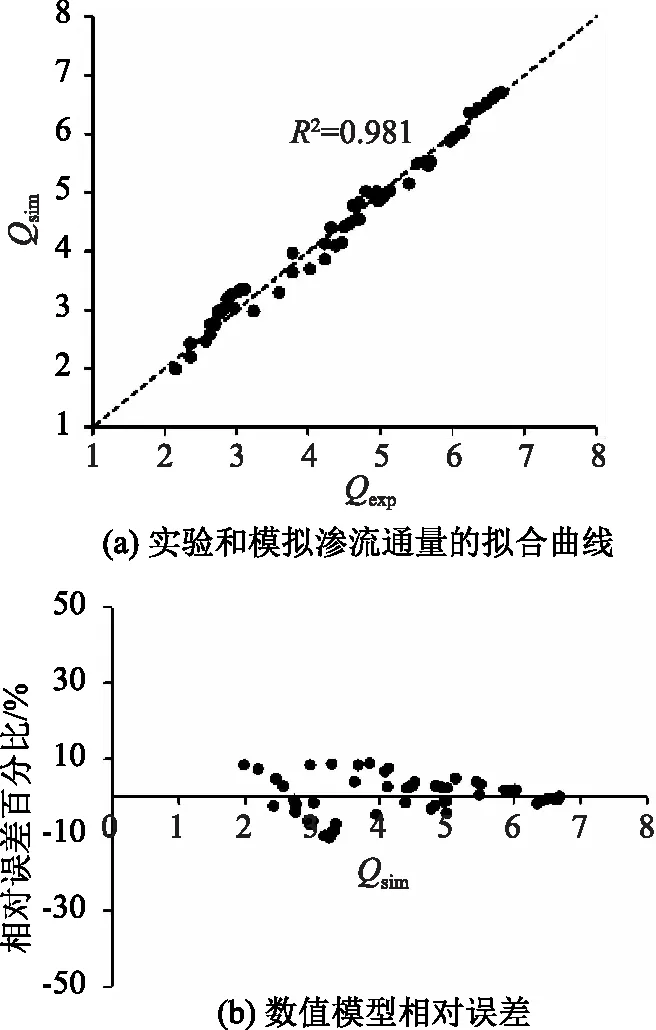
图2 渗流通量的实验值与模拟值比较

由图2可知，渗流通量的实验值(Qexp)和模拟值(Qsim)之间具有良好的一致性，确定系数为0.981，平均相对绝对误差为4.22%。试验与数值模拟结果吻合较好，说明了该方法在求解渗流问题时具有较高的应用价值。

2.1.2水力梯度

从数值模型中获得的单个和组合模式下每个排水孔位置处的水力梯度值如图3所示。

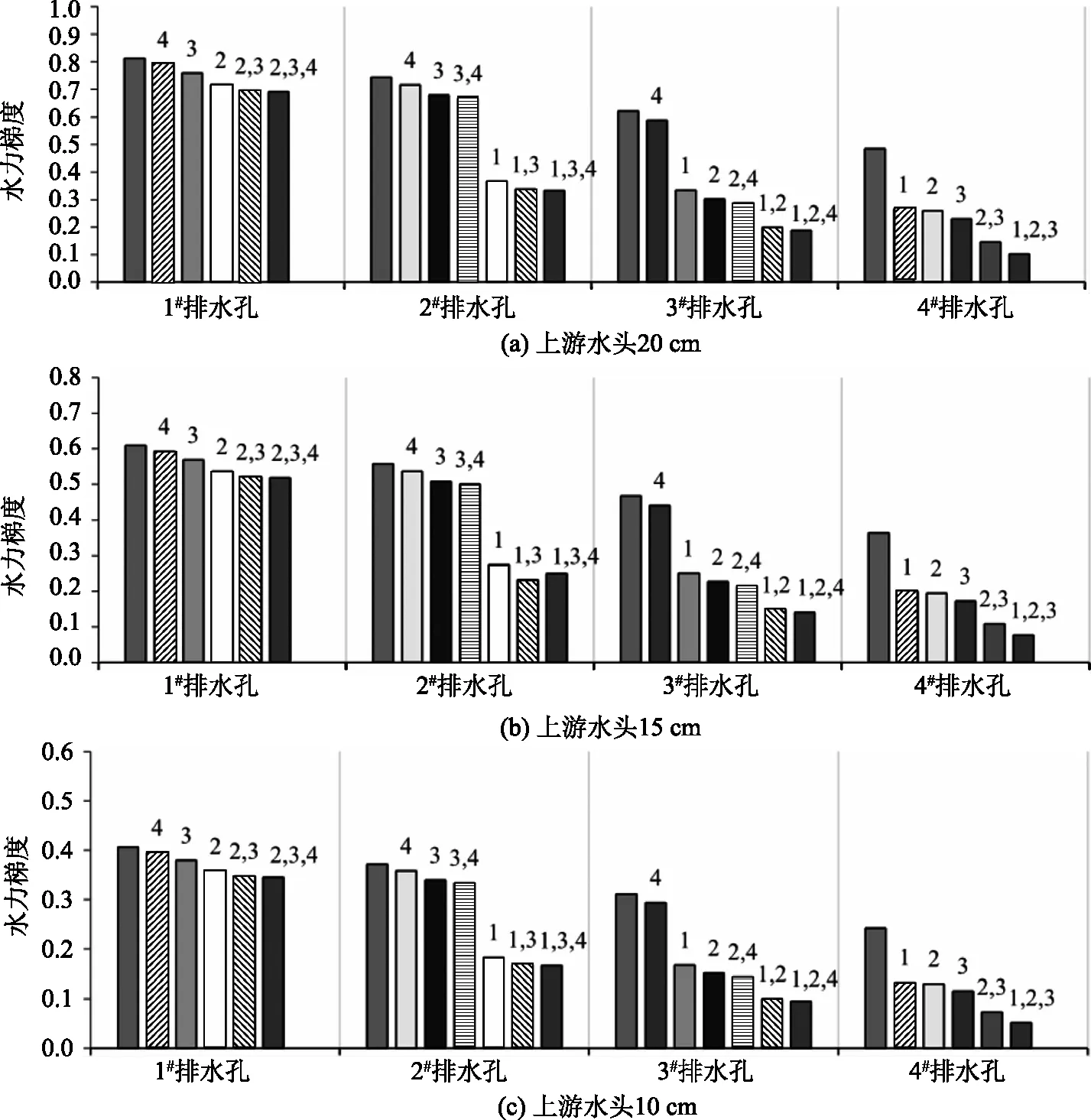
图3 3个上游水头单一模式和组合模式排水孔位置的水力梯度值

在单一模式中，1#排水孔的水力梯度最高，4#排水孔的水力梯度比1#排水孔低约40%。随着排水孔与坝脚之间距离的增加，单一模式和组合模式中的水力梯度均有所下降。在1#排水孔的二元组合中，当2#排水孔与1#排水孔同时打开时，水力梯度最低。此外，1#排水孔组合的水力梯度不会随着排水孔数量的增加而显著变化。1#2#组合模式与1#单一模式相比，1#排水孔的水力梯度降低约12%。在1#2#3#和1#2#3#4#排水孔中，水力梯度几乎恒定，仅略有降低。然而，在2#与3#或4#排水孔的组合中，由于排水孔与坝脚的距离增加，2#位置的水力梯度显著增加。在3#排水孔中，2#3#组合模式水力梯度最低，与3#排水孔相比减少了约51.4%。在三元组合中，1#2#3#组合具有较低的水力梯度。在4#排水孔中，二元组合之间没有显著差异。然而，最小梯度属于3#4#组合，与4#的单一模式相比降低了约52.6%。通过增加排水孔的数量并结合4#排水孔，该排水孔位置的水力梯度已降低，并在1#2#3#4#组合中达到最低值。

从数值模型中获得的所有单一和组合模式的消力池下游水力梯度值如图4所示。

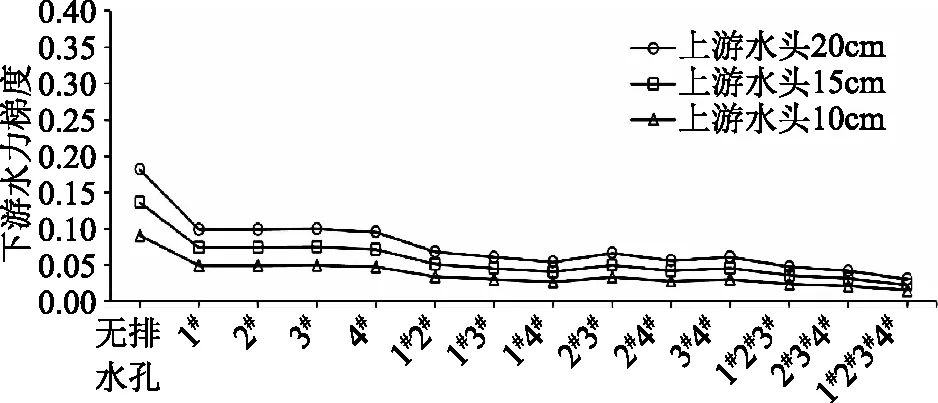
图4 上游3个水头消力池下游水力梯度值

由图4可知，单一模式排水孔的下游水力梯度几乎相同，与无排水孔打开时相比，平均值下降了45.4%。二元组合与单一模式相比，下游水力梯度显著降低，但这种降低与三元和四元组合相比并不显著。在二元组合中，最低下游水力梯度属于1#4#和2#4#组合，与无排水孔模式相比减少约70%。然而，二元组合的下游水力梯度之间没有显著差异。研究发现，当排水孔和防渗墙结合，排水孔可以更好地发挥积极作用执行下游防渗墙的任务。

2.1.3扬压力

从数值模型中获得的单一和组合模式的扬压力(DPU)的衰减百分比如图5所示。一般情况下，扬压力会随着坝脚到排水孔的距离增加而增加。在单一模式下，在1#和4#排水孔处分别观察到扬压力的最大和最小降低值。

由图5可知，通过组合排水孔并增加上游水头，扬压力下降百分比增加。在二元组合中，1#排水孔的组合对扬压力的降低影响最大。此外，横向间距对降低扬压力的影响小于纵向间距。

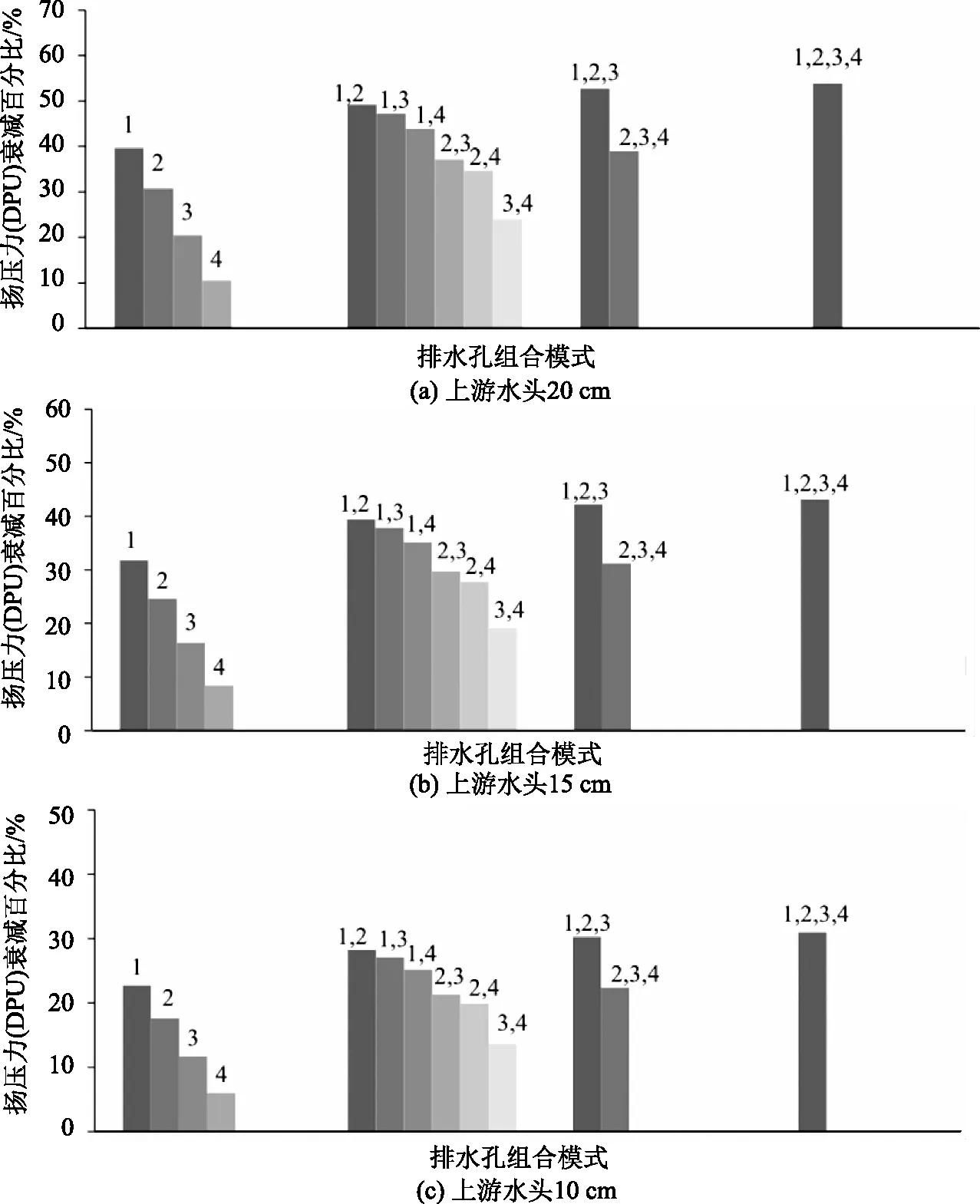
图5 3个上游水头的不同排水孔组合模式的扬压力变化

最佳组合1#2#与1#单一模式相比，扬压力降低了约24%。增加排水孔的数量时，扬压力变化不显著。因此，对扬压力的影响方面，1#2#组合仅比1#2#3#组合高7%，比1#2#3#4#组合高9.6%。从最小渗透损失和下游水力梯度来看，1#4#组合是最佳选择；从排水孔出口水力梯度的数量而言，1#2#组合是最佳选择，因为该组合水力梯度最低；从降低扬压力来看，1#2#组合最优。值得注意的是，这种组合对降低扬压力的影响比1#4#组合高约12.1%。综上所述，基于降低排水孔水力梯度和扬压力降低的必要性，1#2#组合是最佳选择。

2.2 排水孔和防渗墙

防渗墙和1#2#组合对墙末端、下游和排水孔3个位置水力梯度的影响如图6所示。

由图6可知，防渗墙将下游的水力梯度降低了20%，而同时使用1#2#排水孔，可以将下游的水力梯度降低70%以上。防渗墙和排水孔的组合可以有效控制排水孔的渗透损失以及下游水力梯度。

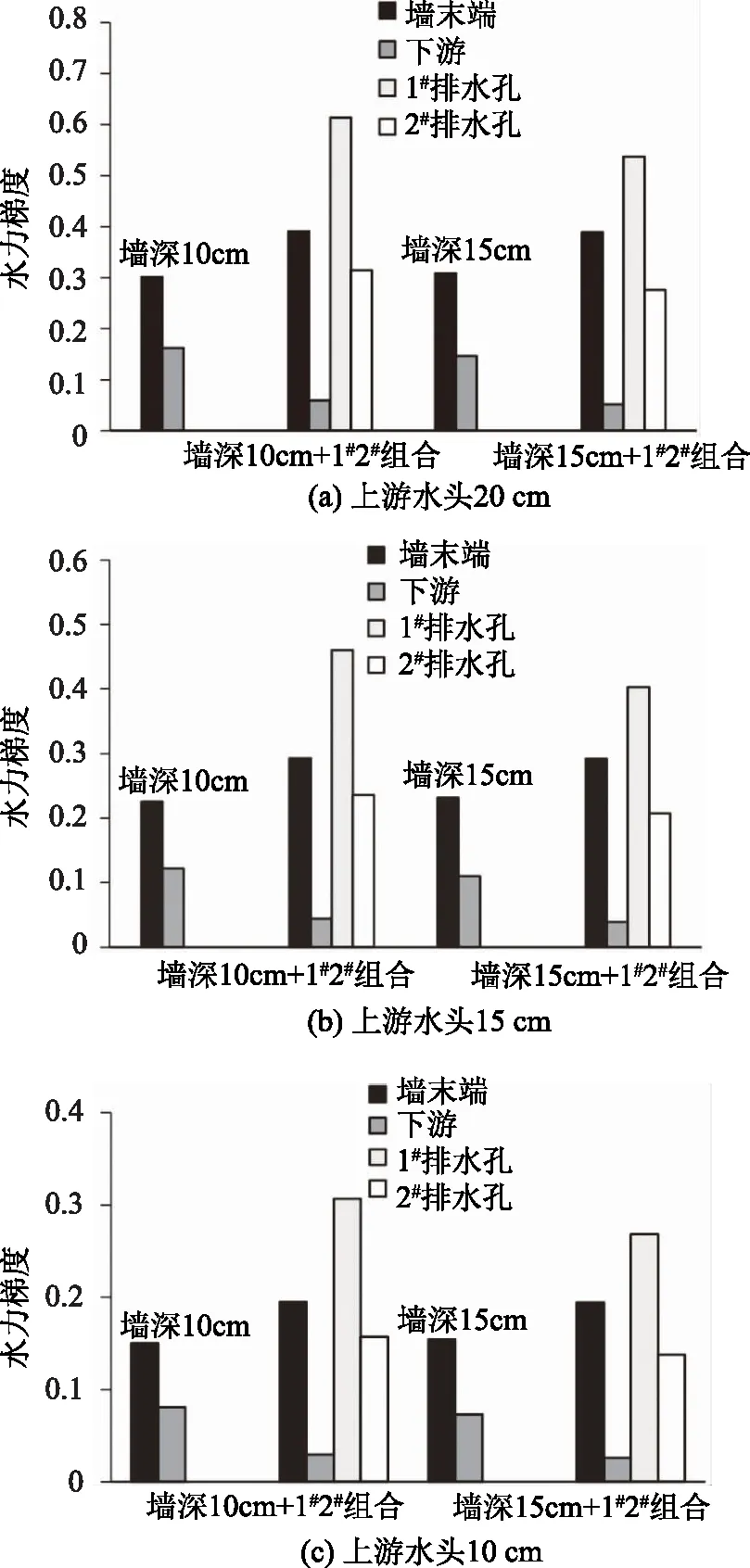
图6 3个上游水头的防渗墙和1#2#组合对不同位置水力梯度值的影响

使用防渗墙和1#2#排水孔时的扬压力变化如图7所示。

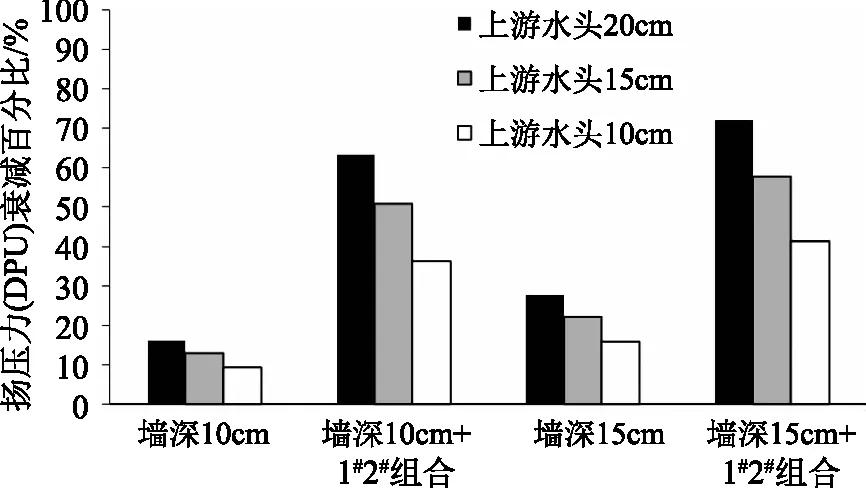
图7 采用防渗墙和1#2#组合后坝下扬压力的变化

在上游最大水头20cm下，采用深度为15cm的防渗墙，扬压力比无防渗墙无排水孔模式降低约28%，而同时使用防渗墙和1#2#组合，扬压力降低了约72%。

3 结论

本文通过实验和数值模型研究了导流坝排水孔和防渗墙对坝体上扬压力和水力梯度的影响。研究结论为：①渗流通量的实验值与模拟吻合较好；②组合模式下排水孔的水力梯度比单一模式降低的更多；③根据水力梯度和扬压力的结果，1#2#组合是最佳的选择；④同时使用防渗墙和1#2#组合对控制下游水力梯度和扬压力非常有效。

本研究在实验室条件下研究排水孔和防渗墙对导流坝水力梯度和扬压力的影响，能够在改善渗流现象的实际工程中起到一定的指导作用。本文只对1种类型但不同深度的防渗墙进行了分析，后续还可以对不同类型的防渗墙进行组合研究。