丁坝冲刷模式与水流形态分析研究

韩梦君

(新疆维吾尔自治区塔里木河流域干流管理局，新疆 库尔勒 841000)

在河岸上修建丁坝可以减少河岸侵蚀，防止河流横向迁移，改善河道通航条件，将水流引向河流进水口，恢复或改善河流中的水生生物[1- 3]。与此同时，在河岸上修建丁坝会导致局部流速和河床剪应力增加，以及结构周围出现马蹄涡[4- 5]，导致丁坝顶端形成冲刷坑，冲刷坑的发育会导致丁坝的破坏[6]。

目前，已有大量学者对沿直河和曲流河的丁坝进行了大量研究。孙志林等[7]研究了矩形丁坝周围的河床地形特征和最大冲刷深度。施如学[8]采用三维数值模型模拟矩形丁坝周围的水流，计算了矩形丁坝附近的流态和剪应力。宁健等[9]采用室内试验和数值模拟相结合的方法，研究了不透水丁坝和透水丁坝的局部流态和河床变形特征。王丹[10]通过测量具有固定冲刷床的模型丁坝附近的三维流速，研究了沉积物平均粒度和粒度分布对不透水矩形丁坝周围河床地形的影响。以上研究对象均为矩形丁坝，缺乏对三角形丁坝的研究，三角形丁坝可有效控制冲刷坑的形成。这是因为三角形丁坝可降低横截面积减小和水位升高的风险，有助于防止河流拐弯处水位突然上升等变化。

本文主要目的是研究三角形丁坝周围的冲刷和沉积模式，并与矩形丁坝进行比较。同时测量了三角形丁坝和矩形丁坝周围的三维速度分量，并对各自的水流形态进行检查和比较，从而更加深入地了解三角形丁坝设计参数等相关问题。

1 试验装置

试验在矩形直水槽中进行，以研究三角形丁坝和矩形丁坝周围的冲刷和沉积模式。水槽侧壁为有机玻璃，厚度为0.01m，水槽宽度为0.56m，长度为7.3m。水槽端部安装有滑动闸门以调整水流深度。水槽出口进入一个混凝土水池，水池末端安装了一个53°三角形堰，用于测量流速。该水槽的平面图如图1(a)所示。

图1 试验装置

为了确定三角形丁坝和矩形丁坝周围的冲刷和沉积模式，本文将这些结构分4组安装在水槽壁上，垂直于水槽壁(垂直于水流)。试验中所有丁坝采用非淹没矩形丁坝，其有效长度为水槽宽度的20%(Le=0.112m)，丁坝间距为有效长度的3倍(Sl=0.336m)。三角形丁坝在水槽壁和水槽床之间倾斜，水槽壁上的顶部与水面处于同一水平面。在弗劳德数(Fr)分别为0.176、0.196、0.216和0.235(恒定深度为0.15m)时，分别施加0.018、0.020、0.022和0.024m3/s的流量。试验在清水中进行，试验持续时间恒定为150min，以便比较三角形丁坝和矩形丁坝周围河床地形变化。在每次试验结束排空床层后，使用激光测距仪(精度为0.001m)测量床层地形。

为了研究单个三角形丁坝周围的流动模式，并将其与单个矩形丁坝周围的流动模式进行比较，本文使用了一个长10m、宽0.8m的矩形直水槽。在这些试验中，单个三角形丁坝和矩形丁坝的有效长度为水槽宽度的20%(Le=0.16m)，丁坝与水槽壁呈90°角(图1(b)和1(c))。所有试验均采用电磁测速仪测量三维速度分量。为了消除水流中移动的沉积颗粒造成的干扰，2种试验使用的水槽床均无沉积物(即刚性水槽床)。在恒定水深为0.15m、流量为0.025m3/s和Fr为0.171的条件下，适当测量三维速度分量。

在单个矩形丁坝上进行的试验中，在以下横截面处测量了三维速度分量：0.20、0.50、0.60、0.65、0.70、0.72、0.75、0.78、0.81、0.85、0.90、1、1.10、1.30、1.70、1.90和2.50m。单个矩形丁坝安装在横截面0.72m处。在每个截面上，在距离壁面水槽的以下距离选取至少15条垂直线：0.05、0.10、0.15、0.20、0.25、0.30、0.35、0.40、0.45、0.50、0.55、0.60、0.65、0.70和0.75m。每条垂线上的三维速度分量分别在水槽床上方0.03、0.07、0.11和0.14m处测量。总的来说，每个横截面至少获取了60个速度读数。鉴于每个横截面的连续读数点之间的水平距离为0.05m，而距离结构较近的横截面则选取0.025m的间距。因此，在靠近丁坝的横截面上进行了60多次读数。在单个三角形丁坝的试验中，分别在0、0.20、0.40、0.50、0.60、0.65、0.70、0.75、0.78、0.85、0.90、1、1.10、1.30、1.50、1.70、1.90、2.20和2.50m的横截面处测量三维速度分量。单个三角形丁坝安装在横截面0.72m处。与单个矩形坝的试验类似，在每个截面上至少考虑15条垂直线(间距=0.05m)测量三维速度分量。同样，对于位于靠近结构的横截面处的垂直线，选择0.025m的间距。此外，在每个横截面上，在水槽床上方0.03、0.07、0.11和0.14m的4个点处测量每条垂直线上的三维速度分量。

2 结果与讨论

2.1 冲刷和沉积

2.1.1三角形和矩形丁坝周围的冲刷和沉积模式

在Fr=0.235时所研究矩形丁坝和三角形丁坝周围的冲刷和沉积模式，如图2所示。

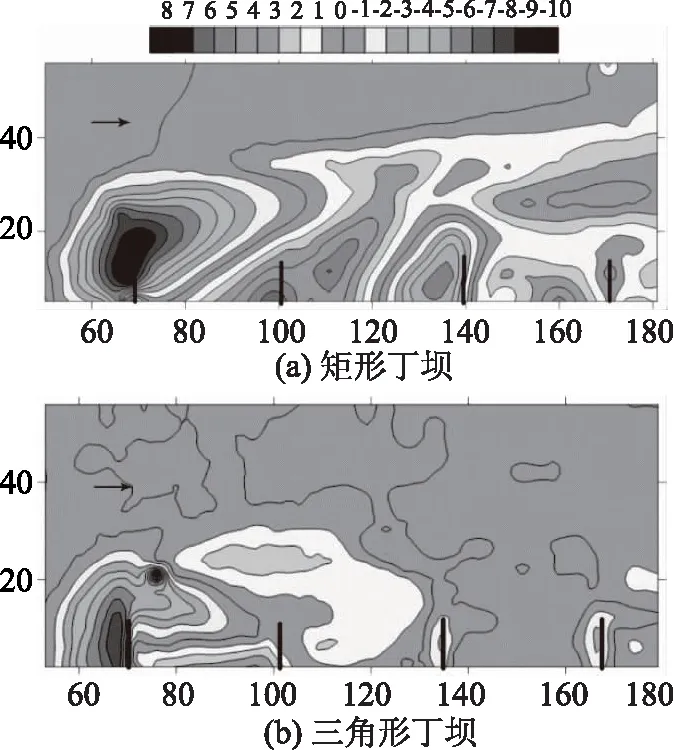
图2 在Fr=0.235处获得的矩形丁坝和三角形丁坝周围的冲刷和沉积模式(高程单位：cm)

不同弗劳德数下矩形丁坝周围的冲刷和沉积模式研究结果表明，无论Fr值如何，在第一个丁坝周围都形成了冲刷坑，且该坑的最大深度出现在结构顶端。随着Fr的增大，该冲刷坑在第一个丁坝上游和下游部分的冲刷坑纵向和横向扩大。第一个丁坝上游和下游冲刷坑的横向延伸持续到水槽壁。增大Fr会增加冲刷坑深度。最大冲刷深度出现在Fr=0.235处。在第二、第三和第四个丁坝周围，Fr=0.176处未观察到冲刷坑。在Fr=0.196时，第三个丁坝顶端出现了一个小冲刷坑。该冲刷坑在Fr=0.216处扩大，在第三个丁坝的上游延伸直至水槽壁，尺寸和深度在Fr=0.235时增加。另一个小冲刷坑出现在第四个丁坝顶端。在所有弗劳德数下，第一个丁坝周围形成的冲刷坑大于其他丁坝。第一个矩形丁坝周围形成的冲刷坑产生的沉积物沉积在该丁坝下游，尤其是第二个丁坝周围。沉积物的体积与第一个丁坝顶端的冲刷速率成正比。

不同弗劳德数下三角形丁坝周围的冲刷和沉积模式研究结果表明，第一个三角形丁坝周围形成了冲刷坑，其最大深度出现在结构上游的丁坝顶端附近。与矩形丁坝不同的是，三角形丁坝周围形成的冲刷坑是不对称的即冲刷坑的大部分位于结构上游，靠近顶端。在这种情况下，在结构的背面(顶端和水槽壁之间)未发现冲刷迹象。Fr增大，冲刷坑的尺寸和深度增加了。最大冲刷深度在Fr=0.235时达到。在Fr=0.196、0.216和0.235处，第一个三角形丁坝上游的冲刷坑不断延伸直至水槽壁。在Fr=0.176和Fr=1.196时，在第二、第三和第四个丁坝周围未观察到冲刷。在Fr=0.216和0.235时，冲刷主要发生在第三和第四个丁坝的顶端，后者的冲刷更严重。第一个丁坝周围形成的冲刷坑也大于其他丁坝。

对比矩形丁坝和三角形丁坝的沉积模式，发现后者周围冲刷产生的沉积物纵向沉积在水槽壁附近，前者的沉积物主要沉积在第二个丁坝顶端或其周围。纵向沉积下来的沉积物将填满侵蚀孔，并沿河流(特别是沿曲流外岸)形成新的河岸。

2.1.2最大冲刷深度

如上所述，在三角形丁坝和矩形丁坝上进行的所有试验中最大冲刷深度发生在上游第一个丁坝周围的冲刷坑处。不同试验中获得的横向最大冲刷剖面如图3所示。图3中，纵轴和横轴分别表示不同点处获得的无量纲河床水平(Z/h)和距水槽壁的无量纲距离(Y/B)。

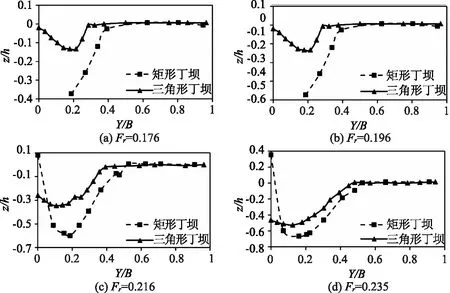
图3 不同试验获得的最大冲刷深度横向剖面图

不同试验获得的最大冲刷深度的变化如图4所示。图4中，纵轴和横轴分别表示无量纲比ds/h(最大冲刷深度与流动深度)和弗劳德数Fr。三角形丁坝的最大冲刷深度小于矩形丁坝。原因可归结为：①在三角形丁坝中，与水流接触的表面积小于矩形丁坝。因此，水流对三角形丁坝的影响较小，削弱了结构周围形成的涡流。②三角形丁坝附近的流速增加幅度小于矩形坝，从而导致河床剪切应力减小。

图4 不同试验获得的无量纲最大冲刷深度随弗劳德数的变化

2.1.3冲刷坑体积

不同试验中获得的冲刷坑体积随弗劳德数的变化如图5所示。

图5中纵轴表示冲刷坑体积与水流深度3次方的无量纲比(V/h3)。可以观察到，三角形丁坝的冲刷坑体积小于矩形丁坝，这可能由于三角形丁坝的表面积较小，受水流冲击较弱，且丁坝附近的流速较低。计算得出，在Fr=0.176、0.196、0.216和0.235时，三角形丁坝冲刷坑体积分别比矩形丁坝减少80.6%、82%、61.5%和54.2%。本研究中不同试验的结果见表1。

图5 不同试验中获得的无量纲冲刷坑体积随弗劳德数的变化

表1 本研究中不同试验的结果

由表1可知，冲刷坑体积随着Fr的增加而增加。最小和最大冲刷坑体积分别在Fr=0.176和0.235时得到。

表格的最后一列显示了三角形丁坝相对于矩形丁坝的最大冲刷深度的减少百分比(SDI)，计算公式如下：

SDI=(Δds/ds矩形丁坝)×100

式中，ds矩形丁坝—矩形丁坝中的最大冲刷深度；Δds—三角形丁坝和矩形丁坝最大冲刷深度之差。

2.1.4沉积物沉积

三角形丁坝冲刷产生的沉积物大多纵向沉积在水槽壁附近，而矩形丁坝中大多数沉积物沉积在顶端以及下游结构周围。且矩形丁坝的沉积物横向发育程度大于三角形丁坝。根据丁坝周围的流动模式，河床和悬移质沉积可能发生在丁坝下游(形成点坝)，这对河岸稳定和开发新河岸具有优势。水流水力参数以及结构几何参数的变化会影响点坝的尺寸、其与河岸的距离以及点坝在河道上的分布。因此，有必要研究三角形丁坝和矩形丁坝形成的沉积作用，以及影响其的因素。

不同试验中最大沉降高度与水槽壁之间的距离变化如图6所示。

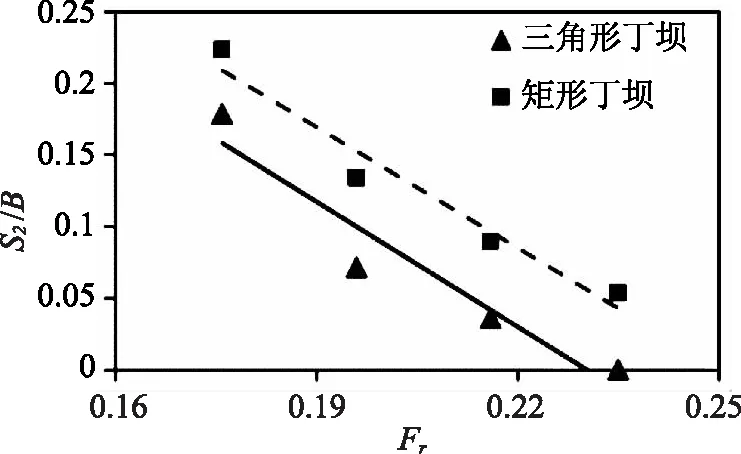
图6 不同试验中最大沉降高度与水槽壁的距离变化

图6中，纵轴为无量纲距离比，横轴为弗劳德数。由图6可知，与三角形丁坝相比，矩形丁坝中的最大沉降高度发生在距水槽壁更远的位置，这说明三角形丁坝具有填补河岸侵蚀孔以及创建新河岸的能力，特别是在曲流外岸。在Fr=0.176、0.196、0.216和0.235处，三角形丁坝的最大沉降高度和水槽壁之间的距离分别比相应的矩形丁坝减少了20%、46.7%、60%和100%。随着Fr的增加，最大沉降高度发生在更靠近水槽壁的位置。因此，在Fr=0.176和0.235时分别观察到最大和最小距离。

在不同试验中获得的最大沉降高度随弗劳德数的变化如图7所示。

图7 不同试验中获得的无量纲最大沉降高度随弗劳德数的变化

在图7中，纵轴表示无量纲比率hs/h(最大沉降高度与流动深度)。结果表明，三角形丁坝的最大沉积高度小于矩形丁坝，这是由于三角形丁坝的冲刷有限，因而侵蚀沉积物有限。在Fr=0.176、0.196、0.216和0.235时，三角形丁坝的最大沉降高度与相应矩形丁坝相比降低了70%、62%、49.3%和41%。在2种丁坝类型中，增加Fr会导致最大沉降高度相应增加。因此，最小和最大的沉降高度分别发生在Fr=0.176和0.235处。

2.2 流动模式

采用垂直于水流构造的单一结构，研究三角形丁坝和矩形丁坝周围形成的流动模式。本文在流量为0.025m3/s和水深为0.15m的情况下，测量了不同截面下的三维速度分量。

结果发现，在矩形丁坝中，距河床0.03和0.14m处的平均流速分别增加了70.3%和84.3%。在三角形丁坝中，距河床相同距离处的平均流速分别增加了15.14%和29.11%。这是因为矩形丁坝仅从顶端引导整个水流从河岸流向河道中部，导致产生了更大的流速，床层剪应力也增加。而三角形的丁坝从上方和顶端引导水流从堤岸向河道中部偏转。因此，与三角形丁坝相比，矩形丁坝附近更容易发生河床侵蚀。

试验时发现在三角形丁坝下游距床层0.03m处有逆流。这些逆流沿着有效长度3倍的最大距离延伸(3Le)。由于逆流与主流的对抗，在三角形丁坝下游(回流区)形成了一个水平旋涡(相对于垂直轴)，从而降低了河岸、上游和下游的流速。该涡流的下游范围是三角形丁坝有效长度的5.5倍(5.5Le)。

目前，还没有确定三角形丁坝设计参数(如距离、有效长度等)的通用标准。下游水平涡流的延伸可作为选择三角形丁坝之间适当间距的标准。

3 结论

本文对三角形丁坝和矩形丁坝周围的冲刷和沉积模式进行了研究和适当比较，探究了单个矩形丁坝和单个三角形丁坝周围的三维流动模式。得出以下结论。

(1)三角形丁坝和矩形丁坝都会将接近的上游水流转向河道中部。

(2)三角形丁坝的冲刷坑体积和最大冲刷深度均小于矩形丁坝。三角形丁坝冲刷形成的沉积物纵向沉积在水槽壁附近，而矩形丁坝中的沉积物主要发生在尖端和下游结构周围。

(3)下游水平涡流的延伸可作为选择三角形丁坝之间适当间距的标准，此结论可为确定三角形丁坝设计参数的通用标准提供依据。