Entanglement and thermalization in the extended Bose-Hubbard model after a quantum quench: A correlation analysis

Xiao-Qiang Su(苏晓强) Zong-Ju Xu(许宗菊) and You-Quan Zhao(赵有权)

1College of Physics and Information Engineering,Shanxi Normal University,Taiyuan 030031,China

2Key Laboratory of Spectral Measurement and Analysis of Shanxi Province,Shanxi Normal University,Taiyuan 030031,China

Keywords: quantum quench,quantum entanglement,thermalization,extended Bose-Hubbard model

1.Introduction

The recent developments achieved in trapped ultracold atom gas experiments[1,2]have rapidly opened possibilities to explore many body physics in a highly controllable way.They have boosted a theoretical interest in the thermalization of the isolated quantum systems out of equilibrium.Quantum quench,[3-14]which is achieved by suddenly changing the parameters of the quantum systems, provides a natural platform to study these nonequilibrium dynamics.In the quench process, the system is prepared in an initial stateρ0,which is mostly the ground state of the initial HamiltonianH0.Then,the model parameters are quickly changed and the quantum system undergoes a unitary time evolution with the new HamiltonianH.After such a quench, the integrable system relaxes to a nonthermal steady state which can be described by the generalized Gibbs ensemble(GGE),[15-18]and the nonintegrable system thermalizes directly.Since thermalization is closely related to the integrability,it is interesting to know how thermalization is affected by the distance of the quenched system from the integrable point.We address this issue by changing the quench parameters away from the integrable point and examining the degree of thermalization.

The thermalization can be explained by the eigenstate thermalization hypothesis (ETH),[19-30]which states that the diagonal matrix elements of the observables are smooth functions of energy, and the off-diagonal elements are exponentially small in the system size.The ETH has been verified in a variety of models of spinless fermions,[22]hard-core[22-26]and soft-core Bosons,[27]spin ladder,[28]and spin chains.[29]The results for some local[25-29]and global[22-24,26]observables have been reported, and the entanglement was also discussed[25]for a two-dimensional hard-core Bose-Hubbard model with a perturbation theory truncated to second order.

A typical feature of the dynamics of the quenched system is the rapid linear growth of entanglement entropy to a stationary value which satisfies the volume law,[31-34]a detailed discussion can be found in the review paper.[33]This feature can be interpreted by the propagation of entangled quasiparticle.[31]The entanglement spectrum of the stationary state is recommended[35]as a criterion to distinguish the thermal state from the integrable[35]and localized states.[36,37]The increasing entanglement entropy is directly measured[38]in a Bose-Einstein condensate of87Rb atoms loaded in a two-dimensional optical lattice.It is demonstrated that entanglement is related to thermalization in the scrambling process[34,39,40]and can be considered as the thermal entropy.Despite this progress, quantitative research on the correlation between entanglement and thermalization is still lacking.We therefore calculate this correlation in the relaxation dynamics of the quenched system by introducing the Pearson correlation coefficient(PCC)as a measurement.

The presentation is organized as follows: In Section 2,we introduce the model and quench proposal.The statistical ensembles used in this work are introduced in Section 3.In Section 4 we comparatively study the validity of the ETH by considering three different types of observables: the Boson number localized at some sites,the nonlocal entanglement between two subsystems and the global momentum distribution functions defined on the whole system.In Section 5,the temporal dynamics of these observables and thermalization fidelity are obtained for different quench parameters.In Section 6, we calculate the correlation coefficients between entanglement entropy and thermalization fidelity for the time evolutions of the quenched system,and a strong correlation is demonstrated.A conclusion and discussion of our results are presented in Section 7.

2.Model and proposal

The realization of nonequilibrium dynamics can be conveniently achieved with cold atoms loaded in optical lattices.[9]By considering the nearest-neighbor interaction,the extended Bose-Hubbard model (EBHM)[41-45]is intriguing for the possible existence of the supersolid phase,[42,43,46,47]which was firstly observed in helium-IV.[48]Its Hamiltonian is

We propose the nonequilibrium process via the paradigmatic setting of quantum quench in a one-dimensional EBHM withN=5 Bosons filled in a lattice withL=9 sites under the open boundary condition.We assume that the system is prepared in a mass-density-wave insulator phase ground state of an initial Hamiltonian withJ0=0 andV0=0.2, which is a product state of each sites.Then at timet=0, it is suddenly quenched to a finalJand keepsV=0.2.The relaxation dynamics are obtained by considering the unitary time evolution under the new Hamiltonian.The EBHM is integrable forJ=0, and tends to be nonintegrable asJincreases.By controlling the final hopping parametersJmove away from the integrable point, we investigate the different thermalization features related to the integrability.

3.The statistic ensembles

3.1.Diagonal ensemble

Due to the recurrence theorem, a finite closed system returns arbitrarily close to its initial state on account of the entirely unitary evolution and never truly equilibrates.[53,54]However, we can focus on the transient nonequilibrium dynamics and define the equilibration in the sense of the time average as follows:

For the Hamiltonian with nondegenerate energy eigenvalues and nondegenerate energy level differences,ρDis also called the diagonal ensemble.[55]

3.2.Microcanonical ensemble

Thermalization is considered[56-58]to take place when the diagonal ensemble gives the same predictions with the microcanonical ensemble for any local operator ˆA,as

where the microcanonical ensemble can be defined as

whereE0is the mean energy of the quenched system, ΔEis the width of the energy window centered atE0,andNE0,ΔEis the number of the energy eigenstates in the window.

3.3.Canonical ensemble

Another important thermal ensemble is the canonical ensemble as

4.Eigenstate thermalization hypothesis

Let us firstly study the static statistics of the energy eigenstates for the quenched system.We numerically diagonalize the final Hamiltonian and calculate〈ˆni〉α=〈α|ˆni|α〉, which is the expectation value of the local Boson number ˆniat siteiunder the energy eigenstate|α〉with the eigenenergyEα.The results are plotted as a function ofEαin the upper panels of Fig.1.We choose two different final hopping parameters for comparison,J=0.1,which is close to the integrable point,andJ=1.6 in the nonintegrable region.We find that the convergence to the ETH is affected by the integrability.For the weak hopping withJ=0.1(circular dots), the profile gives a thick cloud of points rather than a smooth curve as in the situation with the strong hoppingJ=1.6(squared dots).

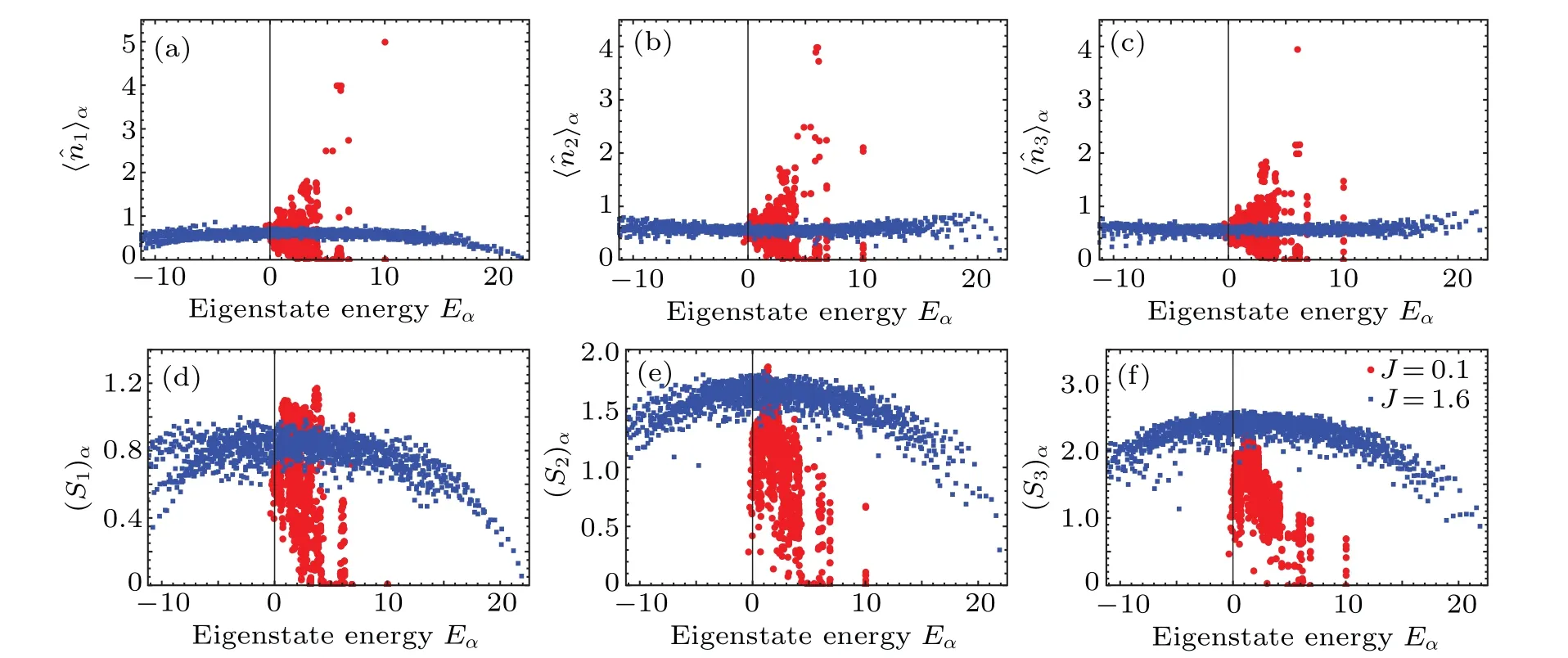
Fig.1.Eigenstate thermalization hypothesis of the local Boson numbers and the entanglement entropy for the different hopping parameters J=0.1(circular points)and J=1.6(squared points).(a)-(c)The expectation values〈ˆni〉α of the local Boson number defined on site i under the energy eigenstate|α〉as a function of the energy Eα.(d)-(f)The entanglement entropy(Sl)α between the l-site subsystem and its complement under the energy eigenstate|α〉as a function of the energy Eα.

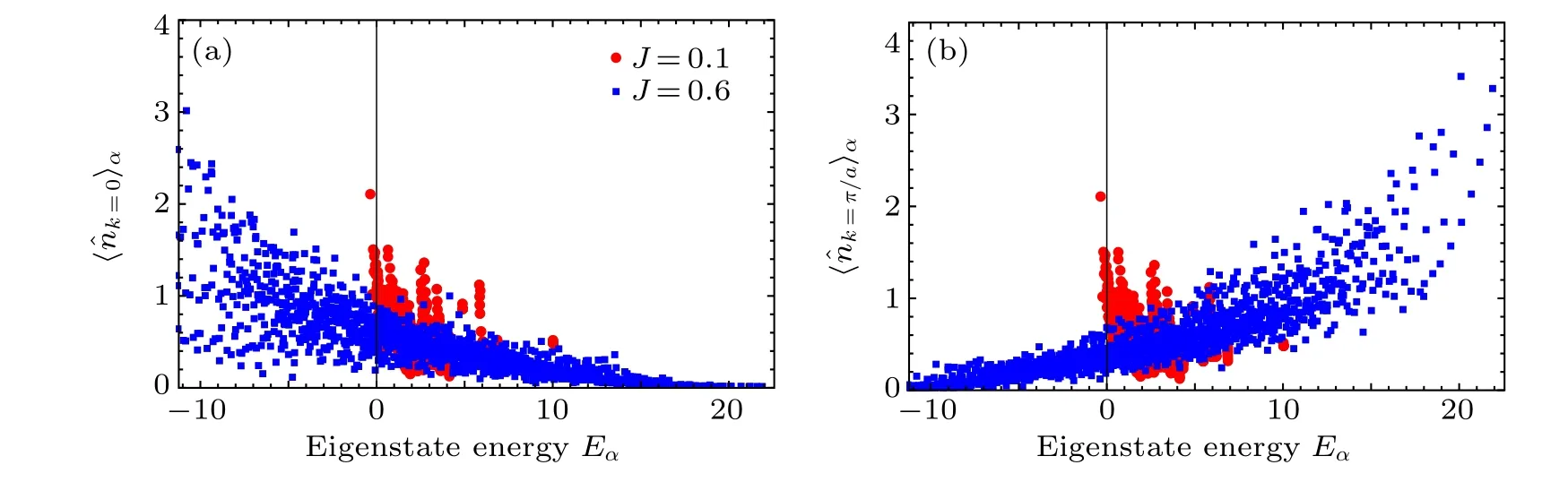
Fig.2.Eigenstate thermalization hypothesis of the momentum distribution functions for the different hopping parameters J =0.1 (circular points) and J = 0.6 (squared points).(a) The expectation values 〈ˆnk=0〉α of the momentum distribution function ˆnk=0 under the energy eigenstate|α〉as a function of the energy Eα.(b)The expectation values〈ˆnk=π/a〉α of the momentum distribution function ˆnk=π/a under the energy eigenstate|α〉as a function of the energy Eα.

It is interesting to verify the validity of the ETH for the nonlocal entanglement.We split theL-site lattice by subsystemAwithlconsecutive sites and the corresponding remainderBwithL-lsites.[59,60]We use the second R´enyi entropy of the reduced density matrixρAas the entanglement entropy,which can be defined as

We calculate the entanglement entropy(Sl)αbetween the subsystem and its complement under the eigenstates|α〉.The features that similar to the results of the local Boson numbers can be observed in the lower panels of Fig.1.The consistency with the ETH for the nonintegrable hopping parameter should lead to the thermalization of entanglement,as we will discuss in the next section.

The momentum distributions are global observables that can be measured conveniently in the cold atoms experiment.The operator of the quasimomentum distribution function ˆnkcan be defined as

whereais the lattice constant.The expectation values〈ˆnk〉αof the momentum distribution functions fork=0 andk=π/aunder the eigenstates|α〉are calculated, and the results are plotted in Fig.2.The thick horn-type distributions indicate the deviation from the standard ETH.

5.Thermalization

Thermalization of the quenched system can be described by the agreement of the expectation values of the local observables with the microcanonical ensemble.We thus directly check the reduced density matrix of the subsystem and calculate the fidelity with the microcanonical ensemble, which is obtained as follows:

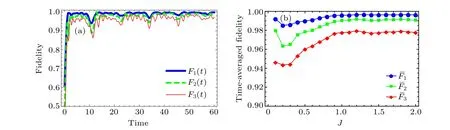
Fig.3.The fidelity of the reduced density matrix of the subsystem with the microcanonical ensemble.(a)The time evolutions of the fidelity Fl for the subsystems with the site numbers l =1 (thick line), l =2 (dashed line) and l =3 (thin line), the final hopping parameter J=1.6.(b)The time-averaged fidelity ¯Fl within a period of evolution time T =1000 for different final hopping parameters J.

whereρlandρmiclare the reduced density matrix of the quenched system and the microcanonical ensemble, respectively.By beginning with an ordered initial state, the system undergoes local information scrambling to the nonlocal degree of freedom in the relaxation process.The fidelity initially increases rapidly and then saturates to 1 with weak fluctuations,as shown in Fig.3(a).We further calculate the time-averaged fidelity ¯Flas a measurement of the degree of thermalization of the quenched system.The results for the different sizes of subsystemland the different final hopping parametersJare plotted in Fig.3(b).We find that the time-averaged fidelity increases with increasingJ, indicating that thermalization is deeply related to the integrability of the quenched system which depends on the hopping parameter.The kinematic analysis by Popescu[56]based on Levy’s lemma[61]has shown that the deviation from the microcanonical state is characterized by the ratio between the system size and the effective size of the environment.It can also be demonstrated that the timeaveraged fidelity increases with decreasing subsystem size.

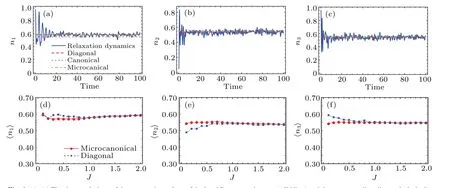
Fig.4.(a)-(c)The time evolutions of the expectation values of the local Boson numbers ni(solid line)and the corresponding diagonal(dashed),canonical(dotted),and microcanonical(dashdotted)ensembles for comparison,the final hopping parameter J=1.6.(d)-(f)The time-averaged(squared)and the microcanonical ensemble averaged(dotted)local Boson numbers versus final hopping parameters J,the total evolution time T =1000.

Let us now continue the characterization of the thermalization by focusing on the temporal evolutions of the observables.Schematic curves for the expectation values of the local Boson numbersni(t)=〈ψ(t)|ˆni|ψ(t)〉are plotted in the upper panels of Fig.4.We find that after a transient undulation,nitends to the microcanonical ensemble and fluctuates around it.Thermalization is thus demonstrated by the agreement of the asymptotic values with the microcanonical ensemble.The time-averaged(diagonal ensemble)and the microcanonical ensemble averaged local Boson numbers〈ni〉for different final hopping parametersJare also plotted in the lower panels of Fig.4.The divergence between the two ensembles tends to vanish asJincreases,with the system moving away from the integrable point.

Similar results are obtained for the time evolutions of the entanglement entropy.As we can see in Fig.5, the entanglement entropy increases sharply from the initial zero and reaches a saturation value with fluctuations.The volume law of the saturated entanglement entropy is verified by the increases which is proportional to the sizes of the subsystems as〈Sl〉t→∞∝l.The time-averaged (diagonal ensemble) and the microcanonical ensemble averaged entanglement entropy〈Sl〉are also plotted in the lower panels of Fig.5.We find that,as the hopping parametersJincreases,the divergence to the microcanonical ensemble vanishes in a similar way as the local Boson numbers.

Fig.5.(a)-(c)The time evolutions of the entanglement entropy Sl and the corresponding diagonal(dashed),canonical(dotted),and microcanonical(dashdotted)ensembles for comparison,the final hopping parameter J=1.6.(d)-(f)The time-averaged(squared)and the microcanonical ensemble averaged(dotted)entanglement entropy versus final hopping parameters J,the total evolution time T =1000.

Fig.6.(a)The time evolution of nk =0.1π/a and the corresponding diagonal(dashed),canonical(dotted),and microcanonical(dashdotted)ensembles for comparison, the final hopping parameter J=0.6.(b)The time-averaged(dotted), the canonical(squared)and microcanonical ensemble averaged (diamonded) momentum distribution functions 〈nk〉 versus k, the final hopping parameter J=0.6 and the total evolution time T =1000.

We also calculate the time evolutions of the expectation values of the momentum distribution functionsnk(t)=〈ψ(t)|ˆnk|ψ(t)〉.A schematic curve for a chosenk=0.1π/ais plotted in Fig.6(a).The time-averaged (diagonal ensemble), canonical and microcanonical ensemble averaged momentum distribution functions〈nk〉versuskare also plotted in Fig.6(b).We find that the time-averaged momentum distribution functions are roughly consistent with the microcanonical ensemble,and their divergences are mainly at the centralk=0 and at the endpointsk=±π/a.Of course, their divergences may appear at otherkfor conservation(on account of the normalization of the distribution function).These divergences can be discerned from the dispersed points in the ETH pictures of Fig.2.It is worth mentioning that,as a global observable,the fluctuation amplitude ofnkdoes not decay quickly with the information scrambling process as the two observables mentioned above,even though the time-averaged diagonal ensemble agrees with the microcanonical ensemble finally(as shown in Fig.6).

6.Thermalization versus entanglement

As the most important resource in quantum information processing,quantum entanglement also plays a central role in the thermalization of the isolated quantum system.It is well known that statistical mechanics relies on the maximization of entropy for a system at thermal equilibrium.However,an isolated quantum system undergoing entirely unitary evolution can be described by a pure quantum state with zero entropy.However, when we consider the quantum entanglement, the subsystems interacting with each other become entangled and local entropy can be created.As a result,the quantum states of the subsystems are decohered to mixed states,allowing the local observables of the subsystem to be described by the statistical physics.Therefore, studying on the correlation between entanglement and thermalization will help us to understand the physical mechanism of thermalization in an isolated system.

We schematically plot the entanglement evolution curve together with the thermalization fidelity in Fig.7.We can find that there are obvious synchronous fluctuations for the early stage revivals in the relaxation dynamics.To describe this correlation, we introduce the Pearson correlation coefficient(PCC)of two variables,which is defined as

The PCC is a number between-1 and +1, which indicates that two variables are linearly related.A correlationr= 1(r=-1)means that the two variables are perfectly positively(negatively)related,andr=0 means that the two variables do not have any linear correlation.

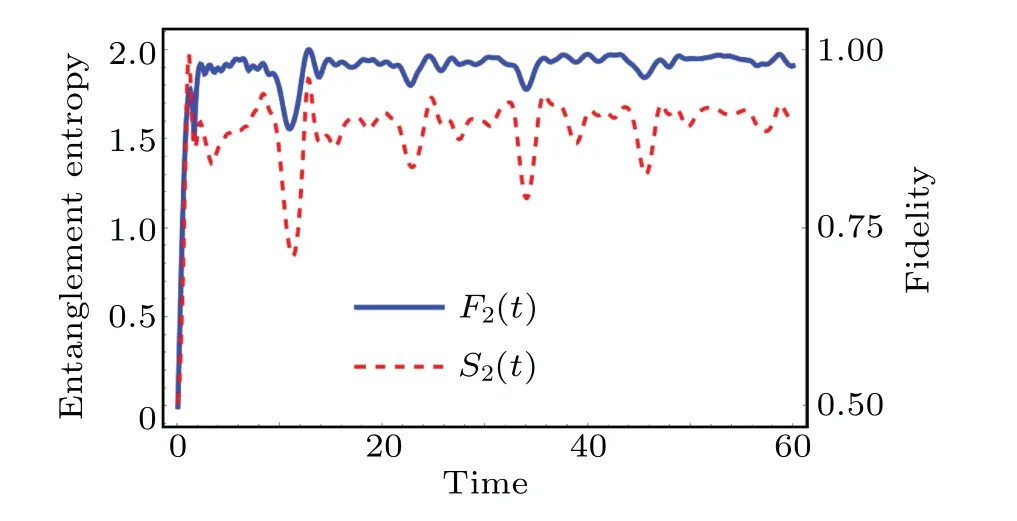
Fig.7.Schematic comparison of the time evolutions of the entanglement entropy S2 and the thermalization fidelity F2,for the final hopping parameter J=1.6.

The PCC between the entanglement entropy and the thermalization fidelity are obtained within a period of evolution timeT=1000 after the quench.The results for the different final hopping parametersJand the different sizes of subsystemlare plotted in Fig.8.We find that all the values of the PCC are close to or above 0.8,indicating a strong correlation between entanglement and thermalization.

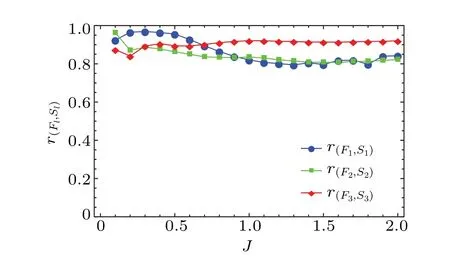
Fig.8.The Pearson correlation coefficients r(Fl,Sl) between the entanglement entropy Sl and the thermalization fidelity Fl for different final hopping parameters J,the total evolution time T =1000.

The correlation between entanglement and thermalization can be explained as follows.The initial state of the quenched system is a product state with zero local entropy, and the asymptotic equilibrium state becomes entangled.The fidelity of the reduced density matrix increases as the quantum state of the subsystem tends to the microcanonical ensemble after the quench, the entanglement which can be denoted by the local entropy increases correspondingly.It results in the synchronous fluctuations of the entanglement entropy and the thermalization fidelity.

7.Discussion and conclusion

We have studied the relaxation dynamics in a onedimensional extended Bose-Hubbard model after the global quench of the hopping parameterJ.The eigenstate thermalization hypotheses are discussed by considering the expectation values of three observables: the local Boson numbers,the entanglement entropy and the momentum distribution functions.The temporal evolutions of these observables are also obtained, and the time-averaged diagonal ensembles are consistent with the microcanonical ensembles for the local Boson numbers, the entanglement entropy and roughly for most of the momentum distribution functions.The fidelity of the reduced density matrix of the subsystem with the microcanonical ensemble is calculated for the different final hopping parameters, and the results show that the degree of thermalization is affected by the distance from the integrable point and the size of the subsystem.A strong correlation between entanglement and thermalization is also verified by introducing the Pearson correlation coefficient of the entanglement entropy and the thermalization fidelity, indicating that entanglement with the environment is very important in the thermalization process.

The correlation between entanglement and thermalization is complicated.The PCC is a measurement that only accounts for the linear correlation,and the values are also related to the chosen measurements of entanglement and degree of thermalization.It is hopeful that this work stimulates further research on this correlation.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No.11147110), and the Natural Science Youth Foundation of Shanxi Province, China (Grant No.2011021003).