Realizing reliable XOR logic operation via logical chaotic resonance in a triple-well potential system
2023-03-13HuameiYang杨华美andYuangenYao姚元根
Huamei Yang(杨华美) and Yuangen Yao(姚元根)
1School of Intelligent Construction,Wuchang University of Technology,Wuhan 430223,China
2Department of Physics,College of Science,Huazhong Agricultural University,Wuhan 430070,China
Keywords: stochastic resonance, logical stochastic resonance, logical chaotic resonance, XOR logic, triplewell potential system
1.Introduction
The interplay between stochastic fluctuations(i.e.,noise)and nonlinearity of a system can produce extraordinary dynamic phenomena.For example, a weak signal can be effectively amplified with the help of noise in the nonlinear system.This phenomenon is called stochastic resonance (SR).[1]SR can be widely observed in various nonlinear systems[2-8]and gives a potential mechanism for utilizing omnipresent noise to obtain constructive outcomes,such as noise-induced enhancement of regularity(i.e., coherence resonance)[9,10]and noiseinduced synchronization.[11]
With increasing miniaturization of computational devices it has become increasingly difficult to suppress or eliminate thermal fluctuation (thermal noise) in computational devices.Noise in computational devices has become one of the main obstacles to further improvement in computational speed and performance.[12,13]Against such a background, Murali and coworkers investigated the intriguing possibility of whether noise can be used to enhance the reliability of logic operation.They confirmed that,as expected,the probability of obtaining the desired logic operation can indeed be obviously enhanced under the assistance of noise in a noise-driven bistable system.They termed this phenomenon logic stochastic resonance(LSR)due to its similarity to SR.[14]
LSR was first proposed in 2009, and has received much attention recently due to its potential applications.[15-25]Some researchers have concentrated on designing new types of LSRbased logic devices.Noise in a LSR-based logic devices can be considered as a positive force and used to obtain or enhance the reliability of logic operation.For instance, Muraliet al.used noisy nonlinear circuits consisting of a linear capacitor,a linear resistor and four CMOS transistors with a battery,to realize reliable and flexible logic gates(AND/OR and NAND/NOR).[26]Guerraet al.realized a noise-assisted reprogrammable nanomechanical logic gate which can execute fundamental logic functions (AND/OR and NAND/NOR),and in which logic functions can be programmed dynamically (such as from AND to OR) by adjusting the underlying nonlinearity of the resonator.[27]In addition,noise-assisted logic devices can be implemented in a Coulomb-coupled quantum-dot rectifier,[28]resonant tunneling diodes[29,30]and Schmitt triggers.[31]LSR-based devices can also be used for the detection of underwater objects.[32,33]These new types of LSR-based noise-assisted logic devices have obvious advantages in terms of energy consumption and size, and thus may be applied in a new generation of energy-saving mechanical computers.[27]On the other hand, some researchers have carried out LSR-related studies from a theoretical perspective, and confirmed that stochastic noise is not necessary for logical resonance.Many deterministic factors, such as periodic force,[34-38]time delay,[39-43]parameters,[44,45]coupling,[46-48]and temperature,[49]can also induce LSR-like phenomena.
It is worth noting that for realization of LSR-based logic devices, most studies have focused on the basic logic gates,such as AND/OR and NAND/NOR, and only a few consider complex logic devices.Compared with bistable systems,multi-stable systems have more potential wells and thus can distinguish between logic input sets (1,0) and (0,1).Because of this,besides the basic logic gates,complex logic operation can also be realized in multi-stable systems.Storniet al.first examined the ability to directly obtain complex XOR logic in multi-stable dynamical systems without the need for the traditional concatenation of NOR/NAND gates.[50]Zhanget al.discussed the effects of Gaussian colored noise[51]and non-Gaussian noise[52]on LSR in a triple-well potential system.We have also investigated the possibility of obtaining logic and set-reset latch operations in a triple-well potential system.[53]
Intrinsic or extrinsic chaotic activities play the role of stochastic noise, and can cause extraordinary dynamic phenomena.[54-58]Chaotic activities in deterministic nonlinear systems can induce chaotic resonance(CR),which is very similar to SR.CR can also be used to amplify or detect weak signals as for SR.Interestingly,chaos can also induce a logic resonance phenomenon(LCR).[59,60]To be specific,if the intensity of chaotic activities is within an optimal window, the reliability of logic operation can be obviously enhanced and the desired logic operation is always achieved.In addition,LCR can be dramatically enhanced via periodic force and coupling between different sub-systems.[61]We have confirmed that LCR can be used to realize a chaos-assisted memory device via the implementation of reliable set-reset latch operation in chaos-driven bistable system.[62]However, realization of a reliable exclusive disjunction(XOR)through LCR has not been reported.In this study,we explore the possibility of obtaining reliable XOR logic operation in a triple-well potential system via LCR.
2.Model and scheme
Considering an overdamped Brownian particle in the following triple-well potential,the Langevin-type dynamical system is described by[52,53]
The parameterγrepresents a dissipation constant.With no loss of generality,γ= 1 is considered in this study.The nonlinear functionF(x) =-0.06x5+0.8x3-2(1+a)xis obtained as the gradient of a triple-well potentialU(x) =x2(0.1x2-1)2+ax2.The parameteracontrols the number and depth of potential wells.As shown in Fig.1, the system can be tristable or monostable by altering the parametera.Unless otherwise specified,ais set to 0.25 through this study.Fora=0.25, the bilateral and middle potential wells are defined by the threshold values of the unstable pointsx±=±2.23607(Fig.1).Two unrelated inputs denoted byI1(t) andI2(t) in Eq.(1)are two-level aperiodic square waves.They can be interpreted as two independent binary logic inputs according to the following rule:I1(t)andI2(t)take the value 0.8 for logic input 1 and-0.8 for logic input 0 (Table 1).The parameterDgoverns the intensity of the chaotic forceX(t), andX(t)is generated from the standard Lorenz system given by[59,61,62]
The parametersσ,ρ,andβtake values of 10,28,and 8/3,respectively,so that the generatedX(t)is indeed chaotic(Fig.2).The dynamics of the system can be obtained by integrating Eqs.(1)and(2)numerically using Euler’s method with a fixed time step Δt=0.001 time units.Note that control runs with smaller time steps disclosed no significant difference in the final results.

Fig.1.Potential U(x) for different values of a.The system can be tri-stable or mono-stable by changing the parameter a.
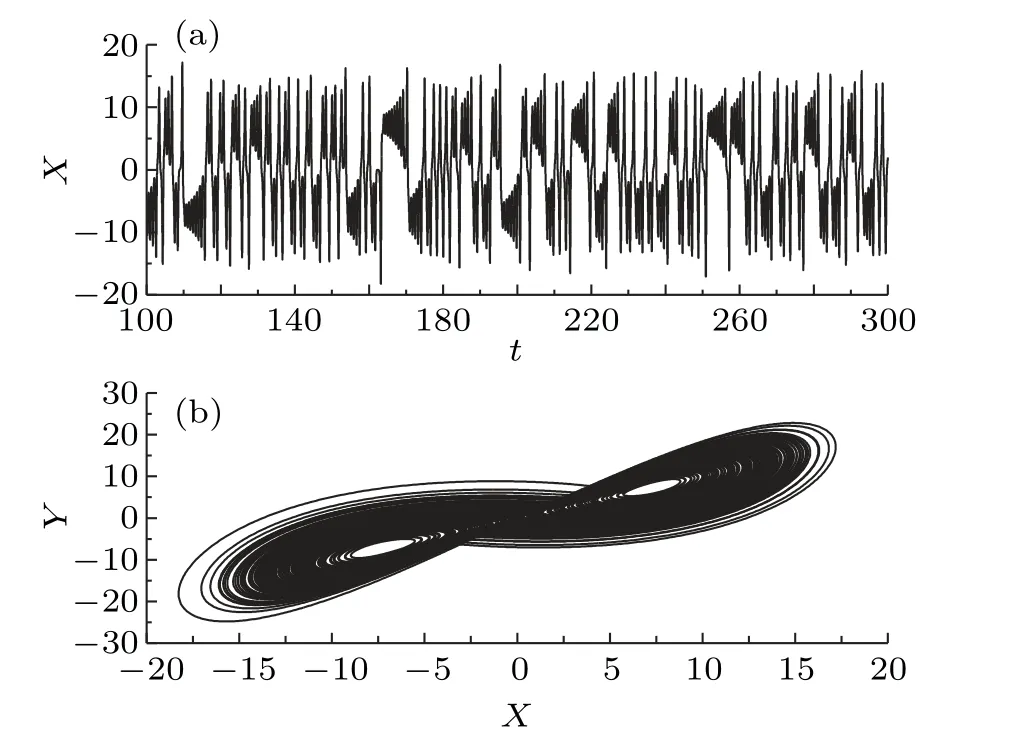
Fig.2.(a)Sampled time series of X(t)generated from a chaotic Lorenz system.(b)A chaotic attractor.
The response of the system to two inputsI1(t) andI2(t)can be interpreted as binary logic outputs according to the following encoding scheme: The response of the system is mapped to logic output 1 if the Brownian particle lies in the central potential well(Fig.1,Table 1)or logic output 0 if the Brownian particle lies in the bilateral potential wells (Fig.1,Table 1).Then, we use the success probabilityP=n/Nto quantitatively characterize the reliability of XOR logic operation.Herenindicates the number of successful runs, whileN=100 denotes the total number of runs.A successful run means that the logic output of the system is always correct for any possible combination of logic inputs(Table 1).Note that there is delayed effect between the inputs and the corresponding response of system.Therefore, we must tolerate the undesired logic results during the transient processes when calculating the success probabilityP.Without loss of generality,the transient processes are defined as the first 10%of the minimum time interval(1000 time units)during which inputsI1(t)andI2(t)remain unchanged.

Table 1.Truth table for a XOR logic gate.

Fig.3.(a)Sampled time series of system output x(black line)and the sum of inputs I1 and I2(red line)under different intensities D of the chaotic driving force. I1 and I2 are two-level aperiodic square waves.Thus, the sum of I1 and I2 is a three-level aperiodic square wave.Clearly, reliable XOR logic operation can be obtained for a moderate intensity D of the chaotic force.(b)Success probability P as a function of intensity D of the chaotic force.The characteristic resonant curve can be clearly observed,indicating the occurrence of logical chaotic resonance for XOR logic.
3.Results
3.1.Chaos-induced logical resonance for XOR logic
As shown in Fig.3(a),when the intensityDof the chaotic force is relatively small(such asD=0.05),the logic output of the triple-well potential system is not always correct according to the truth table of the XOR gate.Increasing the intensityDof the chaotic force (such asD=0.15) can maximize the success probabilityPof obtaining XOR logic operation, and XOR logic operation is always achieved.However, when the intensityDof chaotic forcing is beyond a certain threshold,the desired logic operation is unreliable.In this case,the Brownian particle is mainly controlled by the chaotic force and thus jumps back and forth between bilateral and middle potential wells.The above results indicate that the LCR phenomenon exists in the tri-stable system when the system carries out XOR logic operation.
The success probabilityPis used to quantitatively describe the reliability of XOR logic operation.Pis plotted in Fig.3(b) as a function of intensityDof the chaotic force.It is obvious thatPevolves non-monotonously with increasing intensityDof the chaotic driving force.The curve ofPversusDdisplays resonant characteristics (Fig.3(b)).This result further confirms that LCR can occur in a tri-stable system.More precisely, there is an optimal window of intensityDof the chaotic force in which reliable XOR logic operation can be implemented in a chaos-driven tri-stable system.
3.2.Effects of periodic driving force on logical chaotic resonance for XOR logic
In this section, the effects of periodic driving force on LCR are investigated.To do this, the dynamical Eq.(1) is rewritten as
The last term in Eq.(3)signifies a periodic driving force with amplitudeBand frequencyω.Contour plots of success probabilityPare drawn in theB-Dplane for different frequenciesω(Fig.4).Increasing amplitudeBallows the optimal window(whereP=1)of intensityDof the periodic driving force to shrink in size and move from right to left(Figs.4(a)-4(f)).However,when the frequency is above certain a threshold,the size and location of the optimal window of intensityDof the chaotic driving force is hardly influenced by increasing amplitudeBand increasing frequencyω.This result can also be observed from contour plots of success probabilityPin the log10(ω)-Dplane (Fig.5).When frequency is relatively low, as frequency increases the optimal window of intensityDbecomes wider, and moves from left to right (Fig.5).As amplitudeBis increased, the change in the optimal window of intensityDwith increasing frequency becomes more and more obvious (Fig.5).In addition, with the increase in amplitudeB,the red region of reliability moves upwards(Fig.5),which means that for relatively large amplitudeB,a relatively high-frequency periodic force is necessary if we want to obtain reliable XOR logic operation (Fig.5).In other words,the optimal frequency has a dependence on amplitude.The dependence between frequency log10(ω)and amplitudeBcan be further revealed by contour plots of success probabilityPin the log10(ω)-Bplane for different intensitiesD(Fig.6).It is worth noting that when the intensityDof the chaotic force is small, the chaotic force is so weak that it cannot induce LCR alone (Fig.3).Namely, the chaotic force is subthreshold.Even for a subthreshold chaotic force,when the amplitude(or frequency)is fixed LCR can still be obtained by adjusting the frequency (or amplitude) (Figs.6(a)-6(c)).However, for large intensityD,LCR cannot be always obtained,regardless of whether or not there is a periodic force (Fig.6(i)).Taken together,a periodic force has a great impact on LCR,and thus LCR can be effectively regulated by changing the amplitude and frequency of the periodic force.

Fig.4.Contour plots of success probability P in the B-D plane for different frequencies ω of the periodic driving force.The red reliable region (where P=1)indicates the occurrence of LCR for XOR logic.All insets share the same color bar.(a)log10(ω)=0;(b)log10(ω)=0.4;(c)log10(ω)=0.6;(d)log10(ω)=0.8; (e) log10(ω)=1; (f) log10(ω)=1.2; (g) log10(ω)=1.6;(h)log10(ω)=2;(i)log10(ω)=3.
We can also observe that the area of the red reliable region in the contour plot ofPchanges with changing parameters (Figs.4-6).To qualify this phenomenon, the area ratios of the red reliable region to the total area of plane are plotted in Fig.7.As frequency log10(ω) increases, the area ratio of the red reliable region initially increases rapidly and finally reaches a plateau (Fig.7(a)), which is in accordance with the results shown in Fig.4.Meanwhile, the area ratio of the red reliable region decreases monotonically as amplitudeBincreases (Fig.7(b)), which is consistent with the results displayed in Fig.5.Interestingly, the area ratio of the red reliable region evolves non-monotonically as intensityDincreases, displaying a resonance-like effect(Fig.7(c)).This result corresponds to the observation in Fig.6.
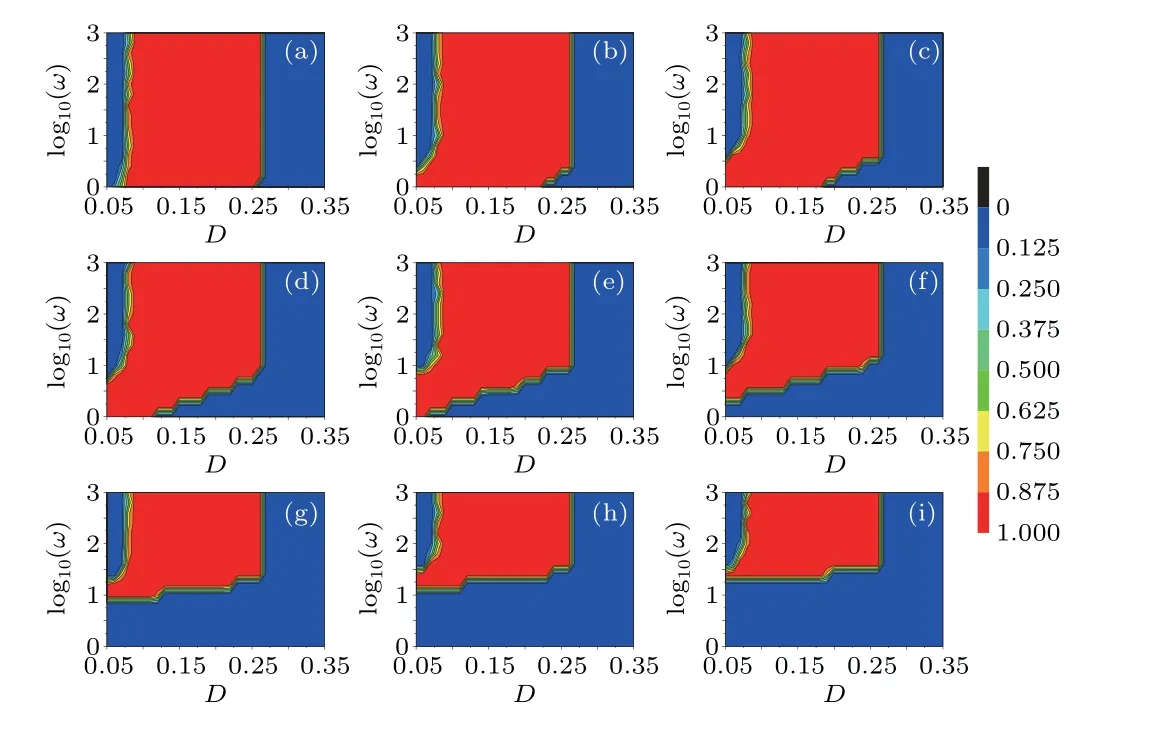
Fig.5.Contour plots of success probability P in the log10(ω)-D plane for different amplitudes B of the periodic driving force.The red reliable region(where P=1) indicates the occurrence of LCR for XOR logic.All insets share the same color bar.(a)B=0.2;(b)B=0.6;(c)B=1;(d)B=1.6;(e)B=2;(f)B=2.6;(g)B=5;(h)B=8;(i)B=10.

Fig.6.Contour plots of success probability P in log10(ω)B plane for different intensities D of the chaotic driving force.The red reliable region indicates the occurrence of LCR.All insets share the same color bar.(a) D=0.05;(b) D=0.06; (c) D=0.07; (d) D=0.08; (e) D=0.09; (f) D=0.12; (g)D=0.16;(h)D=0.26;(i)D=0.28.
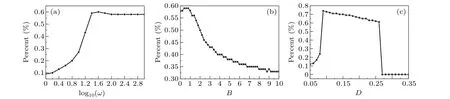
Fig.7.Area ratio of the red reliable region to the total area of(a)the B-D plane,(b)the log10(ω)-D plane and(c)the log10(ω)-B plane.The ranges of B and D in(a)are the same as in Fig.4.The ranges of log10(ω)and D in(b)are the same as in Fig.5.The ranges of log10(ω)and B in(c)are the same as in Fig.6.
4.Conclusion
In this study, we have investigated logical chaotic resonance(LCR)in a triple-well potential system under a chaotic force and periodic force.The probability of successfully obtaining XOR logic operation has been numerically calculated for different parameters.When the system is subjected only to chaotic force,the success probabilityPshows a bell-shaped behavior with varying intensityDof the chaotic force.That is to say, simulation results have revealed that is an optimal window of intensityDof the chaotic force in which the reliability of XOR logic operation can be significantly enhanced.Namely, LCR for XOR logic operation can be realized in a chaotic force-driven triple-well potential system.The effects of periodic force on LCR were explored.When the intensityDof the chaotic force is small,a periodic force with appropriate amplitude and frequency can help to enhance the reliability of XOR logic operation(i.e.,LCR can occur).When the intensityDof the chaotic force is large,LCR never appear.Therefore,a periodic force has a great impact on LCR,and LCR can be effectively regulated by changing the amplitude and frequency of the periodic force.Taken together,a chaotic force and a periodic force allow the triple-well potential system to execute XOR logic operation through LCR.
Acknowledgment
Project supported by the Technology Innovation Team Program in Higher Education Institutions in Hubei Province,China(Grant No.T2020039).
杂志排行
Chinese Physics B的其它文章
- Analysis of cut vertex in the control of complex networks
- Atlas of dynamic spectra of fast radio burst FRB 20201124A
- Investigating the characteristic delay time in the leader-follower behavior in children single-file movement
- Micro-mechanism study of the effect of Cd-free buffer layers ZnXO(X =Mg/Sn)on the performance of flexible Cu2ZnSn(S,Se)4 solar cell
- Thermally enhanced photoluminescence and temperature sensing properties of Sc2W3O12:Eu3+phosphors
- Heterogeneous hydration patterns of G-quadruplex DNA
