Hall conductance of a non-Hermitian two-band system with k-dependent decay rates

Junjie Wang(王俊杰) Fude Li(李福德) and Xuexi Yi(衣学喜)

1Center for Quantum Sciences and School of Physics,Northeast Normal University,Changchun 130024,China

2Center for Advanced Optoelectronic Functional Materials Research,and Key Laboratory for UV-Emitting Materials and Technology of Ministry of Education,Northeast Normal University,Changchun 130024,China

Keywords: Hall conductance,non-Hermitian,topological insulators

1.Introduction

Since the discovery of quantum Hall effect in the 1980s,the topological band theory has been extensively developed and applied in various systems, ranging from insulator and semimetal to superconductor.[1-4]In theory,the Chern number captures the winding of the eigenstates and is defined via the integral of the Berry curvature over the first Brillouin zone.It can not only be used to classify topological materials,but also quantify the response of the system to an external field.For example, the Hall conductance is quantized and proportional to the sum of the Thouless-Kohmoto-Nightingale-den Nijs(TKNN)invariants(or Chern numbers)of all filled bands.[5-7]This theory is previously established in closed systems, and one may wonder if it holds valid for open systems.

Open systems can be described effectively by the non-Hermitian Hamiltonian.Recently, the non-Hermitian topological theories have been introduced and experiments have been conducted in dozens of open systems.[8-47]Many interesting features are predicted and observed in the non-Hermitian systems, including the band defined on the complex plane,[11]the breakdown of the conventional bulkboundary correspondence,[12-17]and the non-Hermitian skin effect.[13,18-25]The definition of the topological invariance for the non-Hermitian systems has also been discussed.[11,32]

From the side of response, the impact of the non-Hermitian on observable has been studied using fieldtheoretical techniques within the linear response theory (e.g.,the Kubo formula).[35-39]They found that there is no link between the non-Hermitian topological invariants and the quantization of observables[35]and the observables are no longer quantized in general otherwise requiring more strict conditions than that of a nonzero non-Hermitian Chern number.[36]In these studies, the non-Hermitian term was introduced via self-energy in the low-energy limit,[37]or phenomenologically introduced to add into the system, so a non-Hermitian version of the TKNN could be derived to show the topological contribution.[36]This rises a question that how the decay rate depends on the momentum of the electron,and how the decay depends on the couplings between the system and the environment, and how a non-Hermitian system withk-dependent decay rate responses to an external stimulus.

In this work, we will answer these questions and shed more light on the response theory for the non-Hermitian twoband systems by the adiabatic perturbation theory.[48-50]The reminder of this paper is organized as follows.In Section 2,we introduce the system-environment couplings and derive a master equation by which we obtain a non-Hermitian Hamiltonian to describe the two-band system subjected to environments.The dependence of the decay rates on the Bloch vectors is also derived and discussed.In Section 3,we work out the response of the non-Hermitian two-band systems to a constant electric field using the adiabatic perturbation theory.The results show that the response of the system can be divided into two terms.The first term is proportional to the non-Hermitian Chern number for two-band systems, which is reminiscent of the relationship between the Chern number and the Hall conductance of closed systems.While the second term can be treated as a correction that suggests the relationship between the Chern number and the conductance might fail for open systems.In Section 4,taking a tight-binding electron in a two-dimensional lattice as an example,we calculate and plot the complex-band structures as a function of the momentum of the electron,kxandky.The Hall conductance of the system is also shown and analyzed.We find that Hall conductance depends on the strength of the decay rate and the electron occupation on the Bloch band,which no longer leads to a quantized Hall conductance in general and a delay in the response of the system to the constant electric field appears.We also compare the Hall conductance of the open systems by the non-Hermitian Hamiltonian and by master equation in this section.In Section 5,we conclude the paper with discussions.

2.Master equation and effective non-Hermitian Hamiltonian

We start with a two-band Chern insulator,whose Hamiltonian can be expressed as(setting ¯h=1)

Here,γ(k) is the decay rate that depends on the Bloch vectors.N(ωn)={exp[ωn/kBT]-1}-1represents the average number of photons in the system.In the Weisskopf-Wigner approximation,N(k) ={exp[2d(k)/kBT]-1}-1.In order to obtain an effective non-Hermitian Hamiltonian, the master equation can be written as

This type of master equation has been studied in Ref.[54],where the environmental electromagnetic field along thexaxis is assumed,Ax=Ext.In the following discussion, we lift this restriction and consider the field along thexandydirections.When the quantum-jump term in Eq.(9) can be neglected,the system reduces to a system described by an effective non-Hermitian Hamiltonian

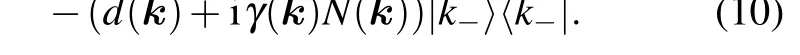
This situation holds valid when we consider the dynamics in a sufficiently short period of time,[57-59]which greatly simplifies the calculation, because it suffices to study the eigenvectors and eigenvalues of an effective Hamiltonian, instead of performing a time-resolved calculation of the density matrix.Here, we consider a Bose reservoir as an environment.Similarly,we also obtain an effective non-Hermitian Hamiltonian for the Fermi reservoir(see Eq.(A5)).

In the limitT →0, we find thatN(k)→0.With this consideration and a unitary transformation,we have

whereαis the dimensionless coupling strength,andωcis the hard upper cutoff.The indexsaccounts for various physical situations,for example for Ohmic spectrum,s=1.We have

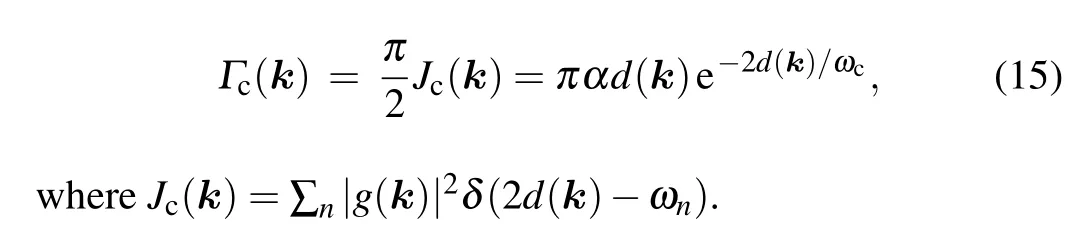
3.Hall conductance

In order to derive the response to a constant electric fieldℰ, one can introduce a uniform vector potentialA(t) that changes in time such that∂tA(t)=-ℰ, which can modify the Bloch vectors, i.e.,k(t)=k+eA(t).The Hamiltonian ˆHeff(k(t))satisfies the following time-dependent Schr¨odinger equation:

Consider a crystal under the perturbation of a weak electric field.We can write the total Hamiltonian as ˆHeff(k(t)) =ˆHeff+ ˆH＇, where ˆH＇stands for the perturbation Hamiltonian.If the system is initially in the ground band,it will always stay in this band if the adiabatic condition is met.But now,we consider the case that there is still a small probability for particles to move from ground to excited band.So we can use the adiabatic perturbation theory with the perturbation Hamiltonian ˆH＇=-i∂/∂t.The corresponding ground band wave function up to the first order in the field strength satisfies[49]

wherehstands for the Planck constant andNis known as the non-Hermitian Chern number defined in Ref.[11].We observe that this response can no longer be proportional to the Chern number of the non-Hermitian system.The responseσHfor the non-Hermitian system can be divided into two terms.The first term is the Chern number of the non-Hermitian system,while the second term can be treated as a correction that suggests the relationship between the Chern number and the conductance might fail for open systems,which is not quantized and a delay in the response can be found.[66]Specific details will be clearer after simplifying Eq.(24),leading to

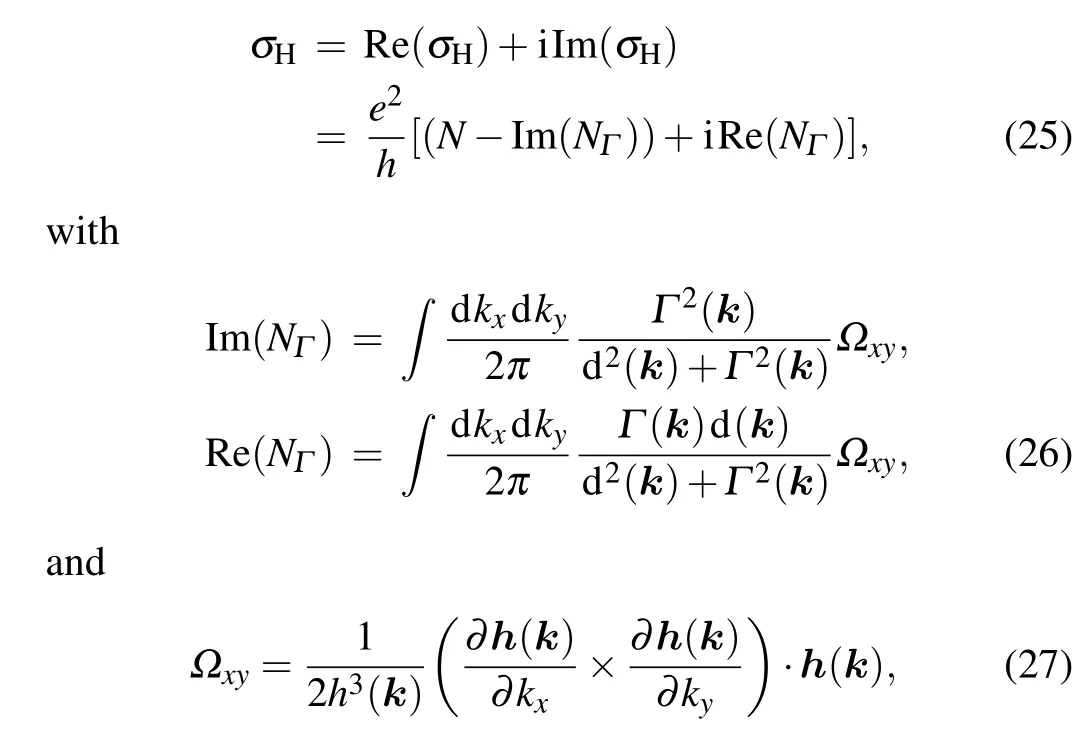
which is the key result of this work.Re(σH)and Im(σH)are the real and imaginary parts ofσH,respectively.The first part Re(σH)is related to the non-Hermitian Chern number, and it is no longer quantized in general.The second part Im(σH)can be understood as the environment induced delay for the system in its response to the electric field, which is reminiscent of the complex admittance in a delay circuit with capacitor and inductor.The energy bands of the non-Hermitian systems are complex in general, which indicates that energy and particle may exchange between system and environment.Due to the decay effect, the Hall conductance is generalized to Hall admittance.So we define the real part of theσHas the Hall conductance and the imaginary part as the Hall susceptance.WhenΓ(k)=0,the Hall conductance returns to the quantized result and the delay disappears,

Next we present a more detailed analysis for the Hall conductance in Eq.(25).First, for a general non-Hermitian two bands system,the Berry connectionAiu-(k)for band|u-(k)〉with energyE-is defined as

In this case, we prove that non-Hermitian Berry curvatures withk-dependent decay rateΩu±(k)and(k)are real and equal to the curvature of the Hermitian system due to thatΓ(k)andd(k)have the same direction, leading to quantization of the non-Hermitian Chern number.

Meanwhile theP(k) term in Eq.(25) depends onΓ(k),withP(k)→1 whenΓ(k)→0.Therefore Re(σH) is not quantized in general and it is no longer proportional to the Chern number of the non-Hermitian system.However, whenΓ(k)→0,we can obtain a nearly quantized Hall conductance.And if the spectral density of the environmentJζ(k)andd(k)is linearly dependent such thatΓζ(k) =ζd(k), whereζis ak-independent constant, we can get a Hall conductance as Re(σH)=[1/(1+ζ2)]n,n ∈(0,±1), i.e., it is not quantized due to the rate[1/(1+ζ2)]in the Hall conductance,but it still possesses a plateau in the dependence of the conductance on the parameter of the system.

From Eqs.(25)and(26),we can find that ath(k)=0 the phase transition occurs

BeacuseΓ(k)/d(k)≪1, the phase transition occurs whend(k)=0 (where the energy gaps close).This condition of phase transition is the same as the corresponding closed systems.Hence, the phase transition points remain unchanged comparing to the isolated system.

Assuming the decay rates are very small, we can ignore the quadratic term of the decay ratesΓ2.In this situation,the Hall conductance reads

In this case,it can be seen that Hall conductance(Re(σH))is proportional to the non-Hermitian Chern number, and it takes quantized values as the change of the parameter.In order to show the validity of the above conclusions,we compare the above results with the Hall conductance by solving the steadystate solution of the master equation,[54,67]

where

with

Although the Hall conductance can be calculated by the master equation description, it can not establish a direct relationship between the Hall conductance and the topological invariant even if we ignore the quadratic term of the decay rates.

4.Example

To demonstrate the response theory of the non-Hermitian two-band system,we consider the following example ofdα(k)

This model describes a time reversal symmetry-breaking system,which might be a magnetic semiconductor with Rashbatype spin-orbit coupling,spin-dependent effective mass,and a uniform magnetization in thezdirection.[68]This model can be realized in graphene with Fe atoms are adsorbed on top,which possesses quantum anomalous Hall effect in the presence of both Rashba spin-orbit coupling and an exchange field.[69]

The corresponding complex band structuresE+=d(k)-2iΓ(k) andE-=-d(k), are shown in Fig.1.Considering that the mode density isξ(k), both Re(E±) and Im(E±) are zero (see Figs.1(a) and 1(b)) at (kx,ky)=(0,π) in the tours surface with the parameterm=2.We conclude that the phase transition point is atm=2,the same as in the closed system.Real and imaginary parts ofE+andE-for allkwithm=3(see Figs.1(c) and 1(d)) have a gap between them and the band structures are the topological nontrivial.The imaginary part of the energy eigenvalueE+, the decay rate, depends on the Bloch vectork(see Fig.1(b)),which indicates that the relaxation time of the particle is different at different positions in the momentum space.Comparing Re(E±)and Im(E±)with the same parameters, we find that they have similar distribution in the momentum space,which is easy to understand because the relaxation time of the particle is relatively short at a higher energy Bloch band under the influence of the environment.

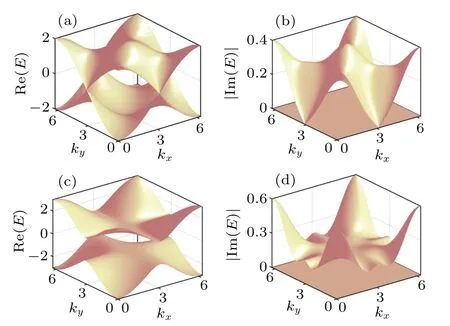
Fig.1.Complex band structures of the non-Hermitian Chern insulator Re(E)± =±d(k), |Im(E+)|=2Γ(k), and |Im(E-)|=0.The mode density ξ(k) is taken to plot this figure.(a), (b) Real and imaginary parts of the gapless bands with an exceptional point on(kx,ky)=(0,π)in the tours surface with chosen parameters m=2,δ =0.05,and t=1.(c), (d) Real and imaginary parts of the gapped bands with m = 3,δ =0.05,and t=1.

The Hall conductance and Hall susceptance defined in Eq.(25) are shown in Fig.2.In the isolated system limit,i.e.,Γ(k)→0, the Hamiltonian model reduces to a Hermitian model.In this case, the real part of the Hall conductance Re(σH) =-1 for 0＆lt;m＆lt; 2, while for 2＆lt;m＆lt; 4,Re(σH) = 1, and Im(σH) remains zero for closed systems,namely,the Hall conductance is quantized without delay.For the open system, however, as shown in Fig.2(a), we find that the phase transition points, i.e.,m=0, 2, 4, remain unchanged,but the Hall conductance is no longer quantized under the influence of the environment.Although the Hall conductance is nearly quantized withδ=0.1.The feature of nonquantization can be clearly observed whenδis increased to 0.3 and beyond.Besides,as Eq.(12)shows,the parameterβisk-dependent, which leads the Hall conductance no longer possesses a plateau in its dependence on the system parameter.The details of the dependence are closely related to the choice of the model and the spectral density of the environment.In Fig.2(b), we show the Hall susceptance Im(σH)which can be understood a delay in the response due to the system-environment couplings.Im(σH)increases withδ(we show here from 0.1 to 0.3), while Re(σH) decreases asδchanging from 0.1 to 0.3.

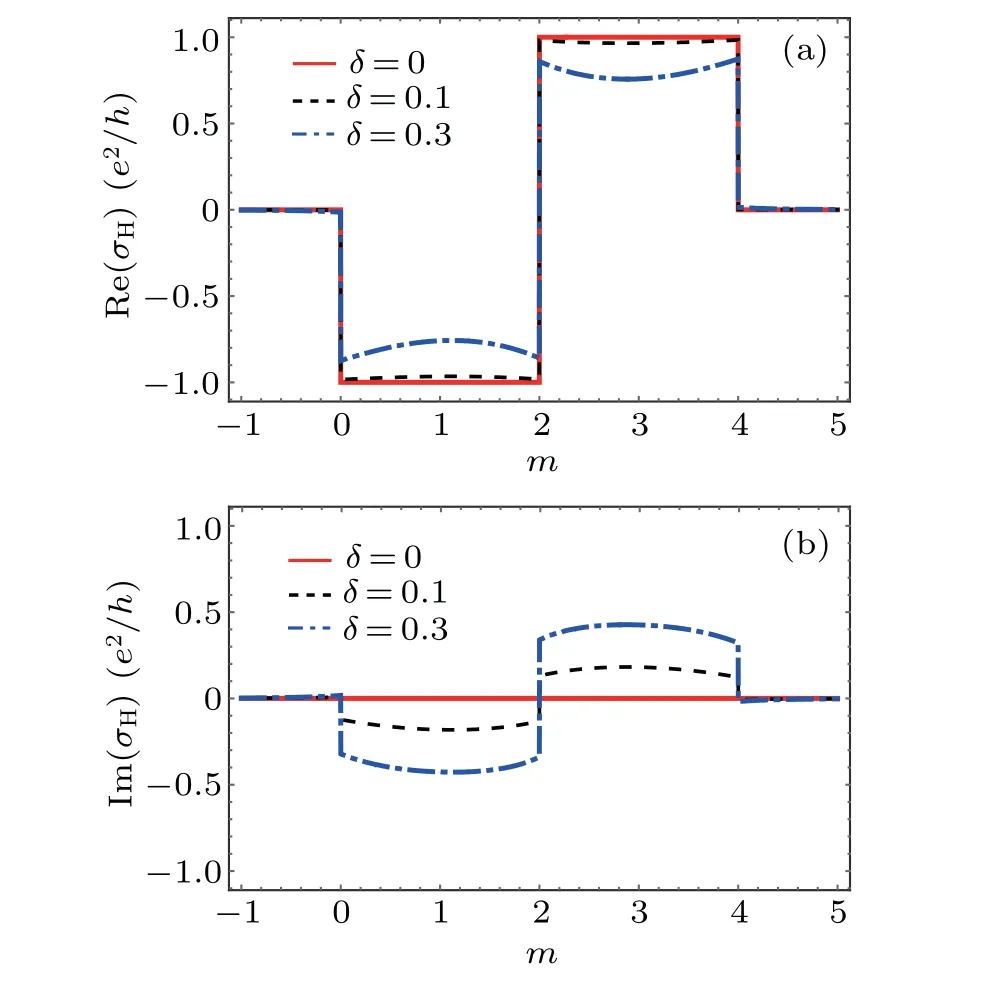
Fig.2.The Hall conductance Re(σH)and the Hall susceptance Im(σH)(in units of e2/h)as a function of m with different δ given by Eq.(25)and with ξ(k) as the mode density.For comparison, the red solid line corresponds to the conventional Hall conductance of closed system(t=1).

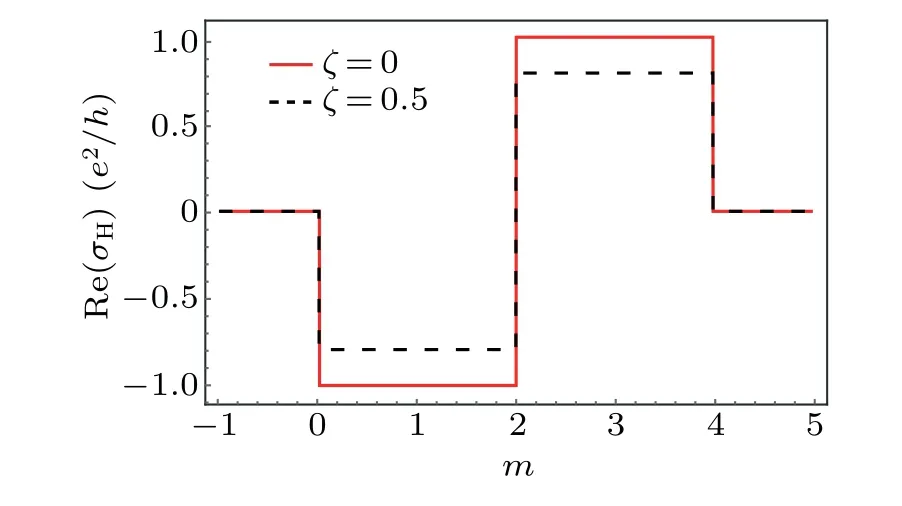
Fig.3.The Hall conductance Re(σH)(in units of e2/h)as a function of m with different ζ given by Eq.(25) with spectral density of the environment Jζ(k).For comparison, the red solid line corresponds to the conventional Hall conductance of the corresponding closed system(t=1).

In Fig.3, we show the Hall conductance of the non-Hermitian two-band systems Re(σH)for differentζ.We consider the spectral density of the environmentJζ(k) andd(k)are linear.One can find that the Hall conductance still possesses a plateau as the change ofm,but its value is no longer an integer,for instance,Re(σH)=0.8 whenζ=0.5.

In Fig.4, we show the Hall conductance for the non-Hermitian two-band systems Re(σH) and the Hall conductance for open systems by solving the master equationσME.The same mode densityξ(k)as that used in Fig.4(a)has been taken to calculate the results in Fig.4(a), while Fig.4(b) for the Ohmic spectral density.One can see that the Hall conductance obtained by the two methods is almost the same,because the quantum-jump term has negligible effect on the first-order steady-state solution of the master equation.Hence in this case,it is a good approximation to approximate the model by a non-Hermitian Hamiltonian.The non-Hermitian Hamiltonian is obviously more convenient to describe such a system, because it is easy to study the eigenvectors and eigenvalues of an effective Hamiltonian and the calculation is straightforward.

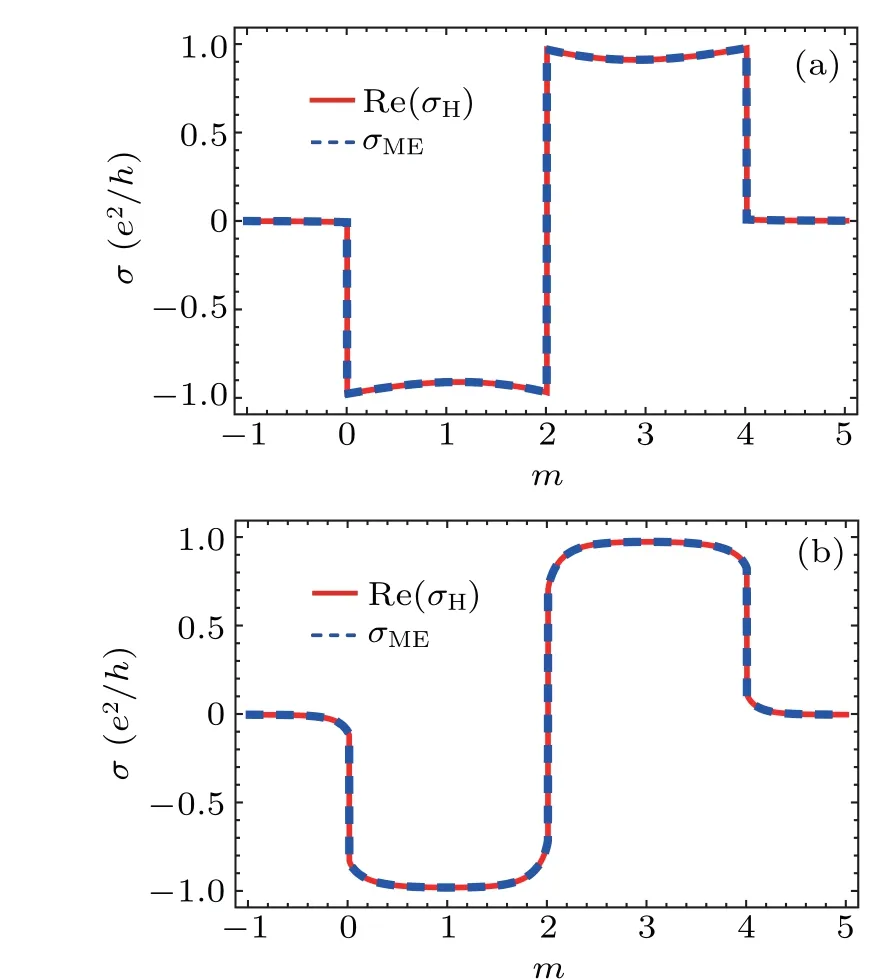
Fig.4.The Hall conductance Re(σH)and the Hall conductance σME(in units of e2/h)as a function of m given by Eqs.(25) and(38), respectively.The red solid line is the Hall conductance for the non-Hermitian two-band systems, while the blue dashed line is for the Hall conductance obtained by solving the master equation.Panel(a)is plotted for mode density ξ(k)with δ =0.2,t=1,while(b)is for the Ohmic spectral density of the environment with α =0.2,ωc=1,and t=1.

5.Conclusions

We have developed the response theory for the non-Hermitian two-band systems and applied it into topological insulators subjected to environments.An effective non-Hermitian system is obtained by simplifying the Markov master equation by ignoring the jump terms and a decay rate that depends on the Bloch vector is given.Based on this formalism, the Hall conductance is calculated by the adiabatic perturbation theory.We find that although the phase transition point does not changes,the Hall conductance that depends on the strength of the decay rate and distribution of the electron on the Bloch band is a weighted integration of curvature of the ground band and it is not quantized in general.In addition, the system-environment coupling induces a delay in the response of the topological insulator to the constant electric field.Finally, comparing the Hall conductance obtained by the non-Hermitian two-band model with that by solving the master equation, we claim that the non-Hermitian Hamiltonian description is a good approximation and it can provide insight understanding for the response of open systems more than that of the master equation description.

Appendix A:System coupled to Fermi reservoir

Appendix C:Derivation of Eq.(C1)

For the system thatΓ(k)andd(k)are proportional, the Berry curvatureΩu-(k)for the band|u-(k)〉with energyEcan be written as

Acknowledgements

The authors acknowledge Hongzhi Shen and Weijun Cheng for helpful comments.This work was supported by the National Natural Science Foundation of China (Grant Nos.12175033 and 12147206).