Effect of thickness of antimony selenide film on its photoelectric properties and microstructure

Xin-Li Liu(刘欣丽) Yue-Fei Weng(翁月飞) Ning Mao(毛宁) Pei-Qing Zhang(张培晴)Chang-Gui Lin(林常规) Xiang Shen(沈祥) Shi-Xun Dai(戴世勋) and Bao-An Song(宋宝安)

1Faculty of Electrical Engineering and Computer Science,Ningbo University,Ningbo 315211,China

2The Research Institute of Advanced Technologies,Ningbo University,Ningbo 315211,China

3Key Laboratory of Photoelectric Detecting Materials and Devices of Zhejiang Province,Ningbo 315211,China

4Ningbo Institute of Oceanography,Ningbo University,Ningbo 315211,China

5Engineering Research Center for Advanced Infrared Photoelectric Materials and Devices of Zhejiang Province,Ningbo 315211,China

Keywords: antimony selenide films,photoelectric properties,Levenberg-Marquardt method and spectral fitting method(LM-SFM),microstructure

1.Introduction

Antimony selenide (Sb2Se3) has emerged as an alternative absorber material due to its high absorption coefficient,appropriate optical band gap,nontoxicity,low cost and earthabundant.[1-3]It is the promising candidate for important applications in diverse areas such as solar energy conversion,thermoelectric cooling, photo detector technology, thermoelectric power generation and opto-electronics in the nearinfrared region.[4]Particularly, it has been a promising absorber layer for solar cells and displays good photovoltaic properties.[5]With the development of magnetron sputtering (MS), thermal evaporation (TE), pulsed laser deposition(PLD)and other film preparation technologies,the Sb2Se3has attracted more and more attention in the field of solar cells in recent years.[6-8]The film thickness affects its optical,electrical properties and microstructure.It is very important to find the law of film properties changing with its thickness for the preparation of high-quality optoelectronic devices.

The research on the Sb2Se3thin films prepared by TE has been widely reported.M.M.Alligavathyet al.studied the structure,morphology and optical properties of the Sb2Se3films prepared by TE.[9,10]Chen Chaoet al.systematically analyzed the photovoltaic relevant physical properties of the Sb2Se3films.[11]R.T.Ananth Kumaret al.compared the structure of Sb2Se3films after annealing.[12]Researchers had also begun to pay attention to the properties of Sb2Se3films prepared by PLD and MS.Yang Keet al.researched the structure,morphology,composition and photoelectric properties of the Sb2Se3films prepared by PLD.[13]Chen Shiminget al.and Liang Guangxinget al.discussed the material and photovoltaic properties of the Sb2Se3films prepared by MS at different substrate temperatures.[14,15]Alapan Duttaet al.analyzed the influence of growth angle(0°-87°range)on the photoelectric properties of the Sb2Se3thin films prepared by MS.[16]However, there still lacks of detailed and systematic study on the change of optical and electrical properties of the Sb2Se3film with its thickness prepared by MS.

The optical and electrical properties of the Sb2Se3films with different thicknesses prepared by MS are analyzed and studied systematically.Firstly, the method and principle of obtaining the properties of the films are presented, and Levenberg-Marquardt method and spectral fitting method(LM-SFM) calculation accuracy is analyzed by simulation.Then,the refractive index(RI),absorption coefficient and optical band gap of the Sb2Se3films with different thicknesses prepared by MS are calculated by LM-SFM,and the variation laws of film properties with thickness are revealed.Finally,energy dispersive x-ray spectrometer(EDS)and Raman spectroscopy are used to analyze the reason why the optical and electronic properties of the film change with its thickness.

2.Principle and simulation

2.1.Principle

The schematic diagram of accurately calculating the RI and absorption coefficient of the Sb2Se3films is shown in Fig.1.By optimizing the square root error between the calculated valuesTfitand the measured valuesT, the RI and absorption coefficient of the film in the whole transmission spectrum can be obtained accurately.The detailed analyses are as follows.

The transmittanceTof the film can be expressed as

whereA=16n2s,B=(n+1)3(n+s2),C=2(n2-1)(n2-s2),D=(n-1)3(n-s2),φ=4πnd/λ,x=e-αd,λis the wavelength,φis the phase,nandsare the refractive indices of the film and substrate, respectively,dis the film thickness,αis the absorption coefficient of the film.The initial value of the absorption coefficientα0is calculated by using the following expression:

Bothdandn0can be calculated by SFM[17]and Cauchy model.Tis the measured transmittance.Three calculated parametersd,n0andα0are substituted into Eq.(1) to obtain the calculated transmittanceT0, and the square root errore0betweenT0andTis calculated.

LM algorithm is used for global optimization to obtainnandαof thin films in strong absorption region.The iteration parameters Δαand Δnare calculated by following equation:

wheregαis the first partial derivative ofTwith respect toα,gnis the first partial derivative ofTwith respect ton,Hαis the Hessian matrix ofα,Hnis the Hessian matrix ofn,µis the step size for optimization.The two optimized parameters areα=α0+Δα,n=n0+Δn.The transmittanceTfitis fitting data from discrete calculated values.These two parametersαandncan be calculated accurately by continuously optimizing the errorebetweenTfitandTthrough iterative calculation.

Fig.1.Schematic diagram of the LM-SFM.(a) Transmission spectrum.(b) Initial RI.(c) Initial absorption coefficient.(d) The calculated value T0 and the measured value T.(e)Transmittance error e.(f)RI and absorption coefficient.

2.2.Simulation

The simulation results are shown in Fig.2.Figures 2(a)-2(c) show the calculated absorption coefficient, refractive index and transmittance, respectively.Figures 2(d)-2(f) depict the corresponding calculation errors, respectively.It can be seen from the figure thatnandαin the whole transmission spectrum are accurately calculated.The calculation accuracy of the refractive index and the absorption coefficient is better than 0.03%and better than 3%by using the LM-SFM,respectively.

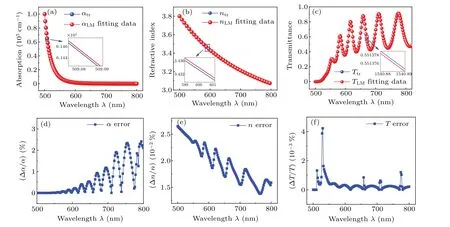
Fig.2.Simulation results.(a) Absorption coefficient.(b) RI.(c) Transmission spectra.(d) Absorption coefficient error.(e) RI error.(f)Transmittance error.

3.Experiment

3.1.Preparation of thin films

The glass target was prepared by using the traditional melting quenching method.In this experiment, high purity Sb and Se powders was used as raw materials.They were weighed accurately on an electronic balance according to the designed composition ratio and placed in quartz glass tubes.The purity of Sb and Se was 99.999%.The quartz tube with raw material was pre-heated to 100°C to remove the water in the raw material.Then vacuumed the quartz tube until the vacuum degree was below 10-3Pa.It was fused with hydrogen and oxygen flame and put into the rocking furnace and heated to 1000°C for 10 h, then took out and quenched in water.After glass demolding,it was annealed slowly to room temperature in the annealing furnace.Finally, the glass was processed into a double-sided polished sample with the size of Φ76.2 mm×3 mm as the target material.

The Sb2Se3thin films were deposited on the SiO2glass substrate by magnetron sputtering.During the preparation process, the chamber pressure was evacuated to lower than 10-5Pa, Ar gas flow was 50 sccm and then the sputtering pressure was 0.5 Pa.The sputtering power was maintained at 40 W.The substrate upon which thin film was deposited and rotated at a speed of 20 r/min and maintained at 25°C during the deposition.The sputtering time was 15 min, 35 min,55 min,75 min and 100 min,respectively.After preparation,the film was placed in a vacuum annealing furnace and annealed at 100°C for 1 h.

3.2.Characterization of thin films

The transmission spectra of the films was measured by spectrophotometer(PerkinElmer Lambda 950), and the spectral range was 500 nm-2500 nm.The phase x-ray diffractometer(XRD)of Bruker D2 and micro-Raman spectrometer were used to measure and analyze the structure of the thin films.The Raman laser wavelength was 785 nm and the laser power was 0.1 MW.The compositions of the thin film samples were characterized by using an EDS installed in a Tescan VEGA3 SB-Easyprobe scanning electron microscope.All tests were conducted at room temperature.

4.Results and discussion

4.1.Optical properties of Sb2Se3 thin films

Figure 3(a) is the transmission spectra of the film.The initial RIn0of the Sb2Se3thin films in absorption region is calculated by SFM and Cauchy dispersion model, and obtained initial absorption coefficientsα0by Eq.(2).Then, according to the LM method, continuously optimize the error between calculated valueTfitand measured valueTthrough iterative calculation.WhenTfitis consistent withT,αandnare obtained accurately as shown in Fig.3(b).TheTfitandTin absorption region are compared as shown in Fig.3(c).Figure 3(d) is the deviation betweenTfitandTin absorption region and the overall deviation is less than 1.5%.

The optical parameters of the films are measured and calculated as shown in Fig.4.Figure 4(a) is the transmission spectra of the films which shows that the absorption cutoff edge moves to the long-wave direction with the increase of the thicknesses of the thin films.Figure 4(b)shows the change of film RI with wavelength.The results indicate that the RI of the thin film decreases with the increase of wavelength and increases with the increase of film thickness at the same wavelength.The absorption coefficientsαof the Sb2Se3thin films of different thicknesses are shown in Fig.4(c) which shows that, at lower wavelength values, and before the absorption edge of samples, the absorption coefficientαhas higher values.These highα-values attribute to the resonance impacts which may occur between the incident photons and the electronic polarizability.Also,theαfor all film samples are found to decrease dramatically at the absorption edge,which due to the occurrence of coupling of the electrons.The absorption depends mainly on the photon energyhνaccording to the Urbach relation

wherea0is a constant andEuis the width of localized tail states which represents the degree of disorder in the noncrystalline material.[32]hνdecreases as the wavelength broadens,soαdecreases as the wavelength broadens.

Based on the magnitudes ofα,the extinction coefficientskof the Sb2Se3films can be deduced from the following relation:

Thekof the Sb2Se3thin film is shown in Fig.4(d).It can be seen thatkdecreases with the increase of wavelength and increases with the increase of thin film thickness.

The relation between absorption coefficient and optical band gap for direct transition is given by the Tauc equation

wherehνis the photon energy,Egis the optical band gap,andB1/2is the Tauc parameter.Plotting(αhν)1/2againsthνand extending the linear part to(αhν)1/2=0 to calculateEgof the thin films,as shown in Fig.4(e).The results illustrate that theEgdecreases gradually with the thickness of the film increases.Tauc parameter is the slope of the line after linear fitting.Egand Tauc values are listed in Table 1.

In addition, RI dispersion values of the Sb2Se3thin films with different thicknesses have also been analyzed using the single oscillator model expressed by the Wemple and DiDomenico(WDD)as follows:[19,20]

whereE0is the single oscillator energy.Edis the dispersion energy.Plotting(n2-1)-1against(hν)2and fitting a straight line with a slope of(E0Ed)-1and an intercept of(E0/Ed),as shown in Fig.4(f).The calculated parametersE0andEdare listed in Table 1.It is clear from this table that bothE0andEddecrease with the increase of film thickness.According to the WDD model,the static RIn0and the static dielectric constantε∞of the film are calculated, which are summarized in Table 1 and their values increase with the increase of the film thickness.

Fig.3.The RI and absorption coefficient α of the Sb2Se3 film by LM-SFM.(a)Transmission spectrum.(b)The RI and α.(c)Comparison of Tfit and T.(d)The deviation between Tfit and T.

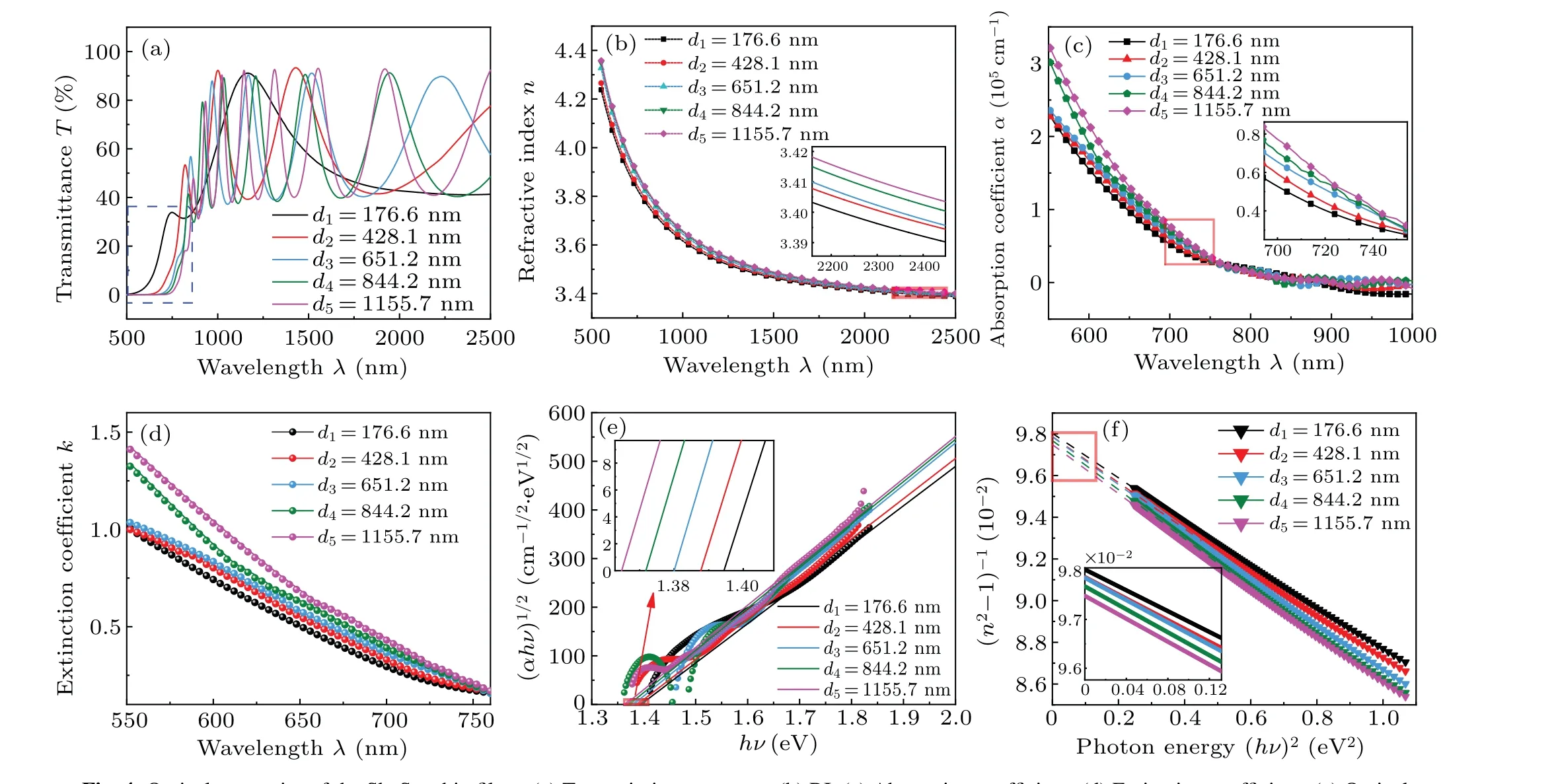
Fig.4.Optical properties of the Sb2Se3 thin films.(a)Transmission spectrum.(b)RI.(c)Absorption coefficient.(d)Extinction coefficient.(e)Optical band gap.(f)The dependence of(n2-1)-1 on(hν)2.

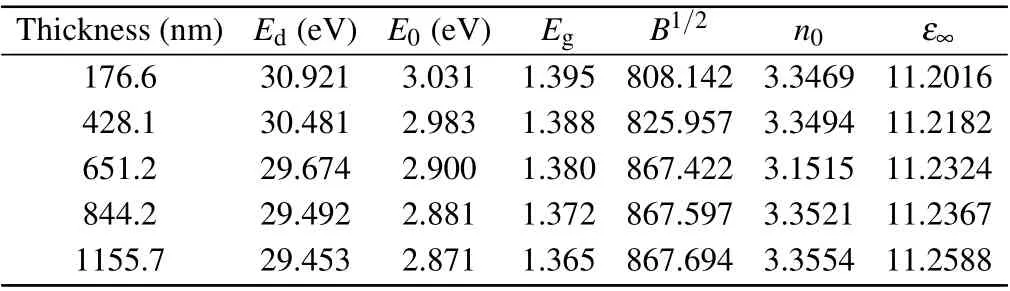
Table 1.Optical parameters of the Sb2Se3 films of different thicknesses.

4.2.Electrical properties of the Sb2Se3 thin films

In the transparent region, the dielectric constant is attributed to free and bound electrons.According to the Spitzer-Fan model, the lattice dielectric constant,εL, and the ratio of the charge carrier concentrations to the effective mass,Nopt/m∗, of the Sb2Se3films with different thicknesses are estimated[21,22]

whereeis the electronic charge,cis the speed of light,andε0is the dielectric constant of vacuum.The magnitudes ofεLandNopt/m∗of the Sb2Se3thin films with different thicknesses are estimated by plotting the relation betweenn2andλ2,the values ofεLandNopt/m∗can be evaluated from the slopes and intercepts,respectively,and are listed in Table 2.

Table 2.Electrical parameters of the Sb2Se3 thin films of differentthicknesses.

Figure 5(a)displays the relation curve between theεLandNopt/m∗, there is an exponential relationship between theεLandNopt/m∗.

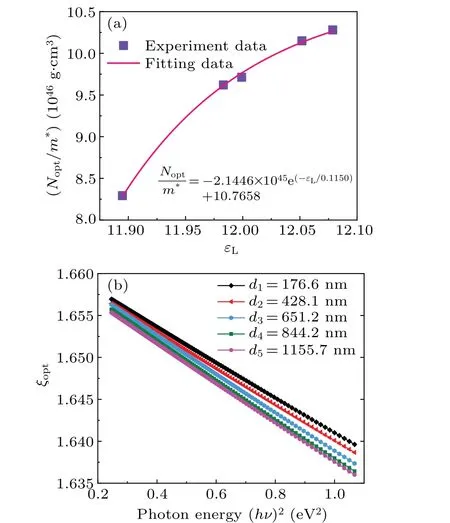
Fig.5.Electrical properties of the Sb2Se3 thin films.(a) The dependence of Nopt/m∗on εL of the Sb2Se3 thin films.(b) The dependence of ξopt on(hν)2 of the Sb2Se3 thin films.

Optical electronegativity,ξopt, is an important parameter to reflect the tendency of an atom to attach electrons from anionic bands.Theξoptof the Sb2Se3films is estimated by[23]

whereAis a constant with a magnitude of 25.54 andnis the RI.Figure 5(b)shows the dependence of theξopton the photon energy(hν)2of the Sb2Se3thin films with different thicknesses, theξoptdecreases with the increase of photon energy and film thickness.

The plasma frequencyωpis known as the frequency of the resonance of the electron free oscillations around their positions of equilibrium and is defined by[24]the results are listed in Table 2, theωpincreases with the increase of the film thickness.

Fig.6.Microscopy and spectroscopy of the Sb2Se3 thin films.(a1) SAED image of thickness 176.6 nm.(a2) HRTEM image of thickness 176.6 nm.(b)XRD spectra.(c)Raman spectra.

4.3.Structure analysis of Sb2Se3 thin films

Figure 6(a) shows the SAED and HRTEM images of the Sb2Se3films with thickness of 176.6 nm.The SAED image shows that the film has characteristic of amorphous structure.Furthermore, there is no regular lattice fringe in the HRTEM image and XRD spectra without sharp peak, as shown in Fig.6(c),which also indicates the film is amorphous.The wide and small ridges at low angle are due to the glassy properties of the glass substrate.[25]The broad peak becomes stronger with thickness, indicating a higher degree of shortrange order.

Although a higher thickness of the Sb2Se3film still reveals an amorphous structure,the relaxation of internal strains and/or the homogenization of defect concentration between amorphous regions may occur,[26]which leads to fewer defects in the film and consequently a higher degree of short-range order.The components of the Sb2Se3films with different thicknesses are measured by EDS.The results are given in Table 3,which shows that the relative content of Se decreases,and the relative content of Sb increases with the increase of film thickness.This is due to the easy evaporation and volatilization of Se.In the preparation process,the longer the sputtering time,the easier Se volatilizes.

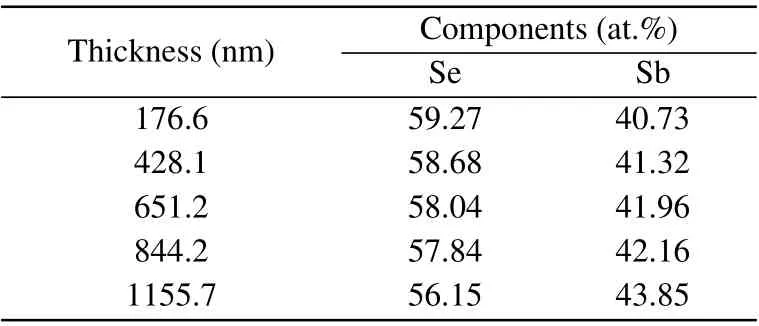
Table 3.Components of the Sb2Se3 films with different thicknesses.

The Raman spectra of the Sb2Se3films with different thicknesses in Fig.6(d) shows that the Raman peaks are mainly in M1:120 cm-1, M2:153 cm-1, M3:190 cm-1and M4:210 cm-1.The peak at 120 cm-1is associated with the Se-Se bonds vibration, and the peak at 153 cm-1is closely related to the Sb-Sb bonds vibration between(Se2Sb-SbSe2)structural unit.[27-29]There is only one main peak at 190 cm-1for the film with the thickness of 176.6 nm,mainly because the Se-Se bonds and Sb-Sb bonds are disordered at a lower thickness not easily to detect, the bonds get order as the thickness increases and Se-Se bonds and Sb-Sb bonds are observed.[30]The intensity of Sb-Sb bonds increases with the film thickness, which because the relative content of Sb increases with the increase of film thickness,resulting in the number of Sb-Sb bonds increases.The main Raman peak and the lower intensity Raman peaks are observed at 190 cm-1.210 cm-1is assigned to the Sb-Se bonds stretching vibration in the SbSe3/2-pyramids.[30]SbSe3/2-pyramids are the basic structural unit of the Sb2Se3phase.[31]With the increase of film thickness, the chemical bond changes from disorder to order,and the structure of the film tends to be stable, which is consistent with the XRD results and the slope of Tauc increases with the increase of thickness.

4.4.The dependence of optical and electrical properties of Sb2Se3 films on the film thickness

The dependence is shown in Fig.7.As shown in Figs.7(a)and 7(b), thenandαincrease exponentially with the film thickness.Figure 7(c) shows that theEgof these films and their thickness maintain a linear relationship.The above two exponential relationships and the linear relationship can be expressed as

The refractive index depends on the density and the average polarizability of the film.As described by the Lorentz-Lorenz equation[32,33]

whereNAis the Avogadro constant,Mrepresents the molar mass,ρrepresents the density, andarepresents the average polarizability.With the increase of film thickness,the relative content of Sb increases,while that of Se decreases.Sb cation has higher polarizability than that of other cations, so the RI of the film increases with the thickness of the film.

Raman analysis shows that the film is more orderliness with film thickness,the greater the orderliness and the smaller band-tail width energyEu.Equation(5)shows that at the same wavelength,Eudecreases with film thickness,butαincreases.The decrease of theEgwith film thickness can be explained by the state density model proposed by Mott and Davis,[34]which shows that the localized state width near the mobility edge is strongly depended on the degree of disorder and the presence of defects in the amorphous structure.The increase of Sb relative content leads to the increase of local state concentration.As the electronegativity of Sb is lower than Se,the band tail and band gap decrease,and the localized states width increases with the increase of Sb relative content.

It is known that the Tauc parameter is a measure of the disorder in the thin films, and the smaller theB1/2is, the disorder will be.Figure 7(d) shows thatB1/2increases with film thickness,indicating the orderliness of the film increases.Meanwhile, the increase of heteropolar bond in Raman spectrum also indicates the increase of the order degree of the film.[6,30]When the thickness is greater than 500 nm,B1/2does not change significantly with the increase of thickness,indicating that thickness has little influence on the internal disorder degree of films with thickness greater than 500 nm.

Fig.7.The dependence of optical and electrical properties of the Sb2Se3 films on the film thickness.(a)n changes as a function of d.(b)α changes as a function of d.(c)Eg changes as a function of d.(d)B1/2 changes as a function of d.(e)Ed and E0 change as a function of d.(f)εL and Nopt/m∗change as a function of d.

The dependence of dispersion energyEdand single oscillator energyE0on the thickness is displayed in Fig.7(e).The results show that both of them decrease with the increase of the film thickness.Figure 7(f) shows that the relationship between theεL, theNopt/m∗and film thicknessd.Both of them increase with the increase of film thickness.This is because the increase of Sb leads to the decrease of the density of strong heteropolar bonds in the film, while the density of weak monopole bonds (such as Sb-Sb bonds) increases.Weaker bonds respond more easily to electric fields than that of stronger bonds, so as the relative Sb content increases, the density of weak bonds increases, leading to dielectric constant increases.

5.Conclusion

The optical and electrical properties of the Sb2Se3films with the thicknesses ranging from 100 nm to 1200 nm are studied in detail by using the LM-SFM proposed in this paper.The thicknessdand optical constantsn,k,α,Egare calculated accurately, the WDD parameters (E0andEd) are also estimated.The dielectric constantεL, optical electronegativityξopt, plasma frequencyωpand the ratio of the charge carrier concentrations to the effective massNopt/m∗of the Sb2Se3films with different thicknesses have also been obtained.The results show thatnandαincrease exponentially with the increase of the film thickness.TheEgof the film and its thickness maintain a linear relationship.When the film thickness is greater than 500 nm, Tauc parameters remain almost unchanged with the increase of film thickness.The WDD parameters decrease andNopt/m∗increases with the increase of film thickness respectively.Finally,XRD,EDS and Raman spectra analysis indicate that with the increase of the film thickness,the relative content of Se decreases, and the relative content of Sb increases,which is the main reason why the optical and electrical properties change with the thickness.The results lay a foundation for further application of the Sb2Se3thin films in phase change memory and solar cells.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.62075109,62135011,62075107,and 61935006)and K.C.Wong Magna Fund in Ningbo University.