Chiral symmetry protected topological nodal superconducting phase and Majorana Fermi arc

Mei-Ling Lu(卢美玲), Yao Wang(王瑶), He-Zhi Zhang(张鹤之), Hao-Lin Chen(陈昊林),

Tian-Yuan Cui(崔天元)1, and Xi Luo(罗熙)1,2,†

1College of Science,University of Shanghai for Science and Technology,Shanghai,China

2Shanghai Key Laboratory of Modern Optical System,University of Shanghai for Science and Technology,Shanghai,China

Keywords: superconducting topological surface states, chiral symmetry, topological nodal superconductor,Majorana Fermi arc

1.Introduction

Since the discovery of topological insulators and their material realization,[1-4]research on topological band structures has become one of the major topics in condensed matter physics.Starting from the pioneering works of Thouless,[5]Haldane,[6]Kane and Mele,[7,8]the “ten-fold way”classification[9,10]of topological insulators and topological superconductors has provided an elegant example of the interplay between symmetry and gapped band systems.The non-trivial topology can be characterized either by the total Chern number(or Z2if time reversal symmetry is present)of the occupied bands,[7,8]or through the bulk-edge correspondence;namely,there are gapless topological edge modes corresponding to the non-trivial topology of the bulk band when an open boundary condition is applied.[11]

Besides the gapped band structure, the topology of gapless bands has also been studied.Weyl semimetals are the most well-known three-dimensional example with a nontrivial gapless band structure.[12]The Weyl node is a monopole of Berry’s phase, and is protected by its non-trivial winding number around the node.From the perspective of bulk-edge correspondence,there are surface Fermi arcs connecting Weyl nodes with opposite chiralities.[13,14]The existence of a Fermi arc is related to a two-dimensional Chern number; namely,if one considers a line connecting the Weyl nodes, and for a given momentum along the line, the Hamiltonian reduces to a quasi two-dimensional gapped system which has gapless edge modes when the bulk Chern number is non-zero,and the gapless edge modes correspond to the Fermi arcs.In other words, the Weyl semimetal is an intermediate state between a topological insulator and a trivial one.[15,16]After Weyl semimetals,the topological nodal-line semimetal has also been proposed.[17]A general relation between the topological classification of gapless systems and the gapped ones has been discussed.[18]

A systematic way of predicting topological materials(including higher-order ones)is by comparing the possible band structures allowed by the lattice symmetry with their atomic limits,which are trivial band structures.[19-21]

Furthermore, the concept of topological states of matter not only prospers in condensed matter physics, but also appears in classical systems and beyond, such as topological Weyl magnons,[22]topological phonons,[23-25]topological photonics,[26,27]and topological non-Hermitian systems.[28,29]Within topological systems, the topological superconductor has drawn much attention.One reason is that the Majorana zero modes and Majorana edge modes in the topological superconductor have potential applications in realizing topological quantum computation.[30-33]

One famous scenario for realizing the Majorana zero mode is that proposed by Fu and Kane, using the proximity effect between a topological insulator and an s-wave superconductor.[34]Following this track, several possible cases of Majorana zero modes have been observed[35-42].In 2018, a 2e2/hconductance was observed in InSb nanowires,which was believed to be evidence of the Majorana zero mode,[43]but this result has been supplanted by the same authors’new data.[44]

Recently discovered iron-based superconductors, such as FeTe0.55Se0.45,[45,46](Li0.84Fe0.16)OHFeSe,[47]LiFeAs,[48]and CaKFe4As4,[49]are new promising candidates for observing Majorana zero modes and Majorana edge modes.[50]One intriguing property of the iron-based superconductor is its endurance against a large in-plane magnetic field(e.g.,more than 20 T in thin film of FeTeSe[51,52]),which is one of the motivations of this paper.

Since the normal state of an iron-based superconductor is a topological insulator,[53,54]we will focus on the superconductivity of the topological surface state(TSS)with an external in-plane magnetic field.We find a topological nodal phase protected by chiral symmetry (with a pseudo time-reversal symmetryT2p =1),and for open boundary conditions,a Majorana Fermi arc connects these two Majorana nodes, similar to the case of Weyl semimetal.[12]The Majorana Fermi arc is also known to be a flat band Andreev bound state[55]which can influence the interface properties drastically.[56-58]The Andreev flat band states have also been considered in two dimensions with p-wave superconductivity[59]or with inhomogeneous magnetic fields,[60]and in three dimensions with momentum dependent pairings[61]or odd-parity pairing.[62]Furthermore, we reveal that the topological nodal superconductor is an intermediate state between two different chiral superconductors, which is exactly a two-dimensional superconductor analogue of a Weyl semimetal.This nodal superconducting phase is also confirmed in a three-dimensional lattice model with thin film geometry,which is possible to realize in iron-based superconductors.The localizations of the Majorana nodes can be controlled by the in-plane magnetic field,which may introduce a non-trivial topological Berry phase between them,similar to the proposal of braiding the Weyl nodes in Weyl semimetals.[63]

This paper is organized as follows.In Subsection 2.1,we construct an effective Bogoliubov-de Gennes(BdG)Hamiltonian for the superconducting TSSs.Although the time-reversal symmetry is broken by the external in-plane magnetic field,a pseudo time-reversal symmetryTpwithT2p =1 remains.Together with the particle-hole symmetry,a chiral symmetry can be defined,which protects the topological nodal superconducting phase.There will be a Majorana Fermi arc connecting the two nodes when open boundary conduction is applied.In Subsection 2.2,we show that the topological nodal superconductor can be viewed as an intermediate state between two chiral superconductors,which provides the topological stability of the nodal superconductor.We discuss the effects of substrates in Subsection 2.3.In Subsection 2.4, we consider a three-dimensional lattice model simulating the thin film of iron-based superconductors,[54]and the nodal superconducting phase is confirmed numerically.The last section is devoted to conclusions,and we provide more details on the band structures of the effective theory in Appendix A.

2.Results and discussion

2.1.Superconducting TSS under an in-plane magnetic field and Majorana Fermi arc

We start from a general effective BdG Hamiltonian describing the superconducting TSSs of a thin film of a topological insulator

The BdG Hamiltonian(1)is time-reversal symmetric,i.e.,T h0(q)T-1=h∗0(-q), withT= iσyχ0τ0K, whereKis the complex conjugation operator.The charge conjugation can also be defined byCh0(q)C-1=-h∗0(-q)withC=σ0χ0τxK.Note that in the normal state,the TSSs in top and bottom surfaces have opposite helicities; therefore there is an emergent mirror symmetry of thexyplane.The superconducting TSS is believed to respect this mirror symmetry; namely, we find thatMxyh0(q)M-1xy=h0(q)withMxy=-iσzχxτ0.[66,67]From the mirror symmetryMxy,one can note that it commutes with the odd-parity pairing termΔσyχzτywhile it anti-commutes with the even-parity pairing term,say,Δeσyχ0τy;therefore the odd-parity pairing term is favored by the mirror symmetry.

Now we consider adding an in-plane magnetic field.Because of the two-dimensional rotation symmetry, we can choose the in-plane magnetic field to be along thex-direction without loss of generality.By adding a Zeeman term toh0,the BdG Hamiltonian becomes

whereλxis the in-plane Zeeman coupling strength.Although the time-reversal symmetry is broken by the external magnetic field, there remains a pseudo time-reversal symmetryTp=σxχxτ0K(which is the combination of time-reversal symmetryTand the mirror symmetry-iMxy) withTphx(q)T-1p =h∗x(-q), andT2p =1.The particle-hole symmetry remains true with the in-plane magnetic field.Therefore the Hamiltonianhx(2)has a chiral symmetryΞhx(q)Ξ-1=-hx(q),withΞ=CTp=σxχxτx.Namely, the system belongs to BDI.[9]The BDI superconductor is also discussed in Refs.[60,68].By substituting the momentumqi →sinqiand the topping termt →t0+t1(2-cosqx-cosqy),we can construct a lattice model of the effective Hamiltonianhx(2).We plot the band structure of the lattice model in Fig.1.From the band structure, one observes that the system is a nodal superconductor(Fig.1(a)), and there is a Majorana Fermi arc connecting the two nodes when choosing open boundary conditions along they-direction(Fig.1(b)),which provides a two-dimensional superconductor analogue of a Weyl semimetal.A more detailed study on the phase diagram of the hopping termt0andt1is provided in Appendix A.

Similar to the case of Weyl semimetal, where the Fermi arc is related to a two-dimensional Chern number,[12]one can find a non-trivial topological number of a one-dimensional system associated with the existence of Majorana Fermi arc.To be more specific, for a givenq0x(except for the Majorana nodes),the BDI Hamiltonianhx(qy,q0x)describes a quasi onedimensional system,and it is classified by Z in 1D.[9]In order to determine the characteristic topological number,we change into the basis that diagonalizes the chiral operatorΞwith the unitary transformationUΞ,

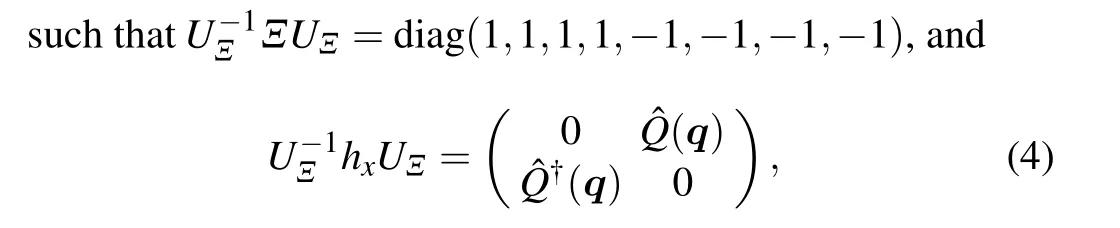
where

From bulk-edge correspondence, if one considers open boundary conditions along they-direction,then for a non-zeroW(q0x), there will beW(q0x) types of Majorana zero mode(s)localizing at each end of the open boundary.W(q0x)can only change in the case when the bulk gap closes.For the parameters chosen in Fig.1(a),W(qx=0)=1 andW(qx=π)=0,which is consistent with Fig.1(b),namely,the Majorana Fermi arc, which comes from the Majorana zero modes at the ends,connects two bulk Majorana nodes,and exists whenW(q0x)/=0 and disappears whenW(q0x)=0.The physics here is similar to that of a Weyl semimetal where the Fermi arc connects two Weyl points with opposite helicities.[12]

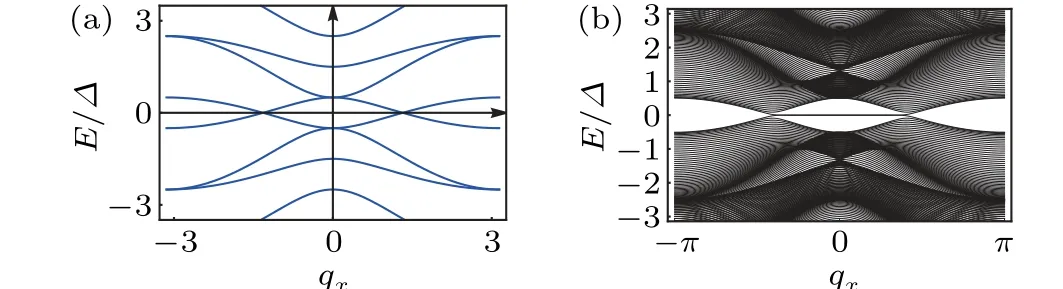
Fig.1.The band structures of hx (2)with µ =0, Δ =λx =1,t0 =t =0.5,and t1 =1.(a)The bulk spectra with qy =0.(b)Open boundary condition along the y-direction with y=50.The two Majorana nodes are connected by

2.2.Interpreting the nodal superconducting phase as an intermediate phase between two chiral superconductors

Since Weyl semimetal can be viewed as an intermediate phase between a topological insulator and a trivial one,[16]one may ask whether the nodal superconducting phase could be interpreted as an intermediate state between two topological distinct phases.The answer is yes, which also provides the topological origin of the stability of the nodal superconducting phase.

In order to show this scenario,we add a spin-triplet intersurface pairing term into the Hamiltonianhx(2),

whereΔtis the spin-triplet pairing strength.This term preserves the mirror symmetryMxy, and breaks both the timereversal symmetryTand the pseudo oneTp; therefore, the chiral symmetry is broken byΔt.The spin-triplet pairing can arise from the Coulomb interaction,and has played an important role in topological superconductivity, such as CuxBi2Se3in 3D[69,70]and bilayer Rashba systems in 2D.[64]

When there are no external magnetic fields, the band spectra nearΓpoint are

whereα=±.The topological phase boundary can be determined by the band touching at theΓpoint;[67]namely, the phase boundaries are given by

which are two circles centered at±Δwith radiustfor fixedΔandtin theΔt-µplane; see Fig.2.In addition, within each circle,there is a topological chiral superconducting phase with a non-zero Chern number.These topological non-trivial phase are protected by the mirror symmetryMxy, and because{Mxy,C}= 0, the topological phase is classified by Z⊕Z.[66,67]More interestingly,whent＆gt;Δ,these two circles intersect.Although the total Chern-number is zero in the intersection,it remains non-trivial because of the mirror symmetry and the Z⊕Z classification.In particular, whenΔt=0, the two circles coincide, and because the system is time reversal symmetric, it is classified by Z2.[9]In addition, there will be topological helical edge states when the parameters are within the circles.

Fig.2.(a)and(b)Topological phase diagrams of h(7)in the Δt-µ plane and Δt-λx plane with Δ =1,t=0.5,(a)λx=0,and(b)µ =0. N stands for the bulk Chern number.Along the Δt =0 line within the two circles is the topological nodal superconducting phase,as confirmed numerically in Fig.1(b),which is an intermediate state between two chiral superconductors.

Now we add in the external in-plane magnetic field.Without loss of generality,we chooseµ=0 for simplicity(the effect ofµis shown in Fig.2(a)).Then the band spectra become

The topological phase boundary is determined as before.We plot the phase diagram in Fig.2 (see Appendix A for more details).From Fig.2(a) one notes that there are two distinct topological non-trivial regions with opposite Chern numbers when the external magnetic field is absent.Furthermore, the non-zero Chern numberNindicates that time-reversal symmetry is broken when the spin-triplet pairing termΔtexists.By turning on the external in-plane magnetic fieldλx,the two topological non-trivial regions are connected without gap closing at theΓpoint (see Fig.2(b)).From the phase diagram Fig.2(b) we have two observations.One is that the topological chiral superconducting phase is protected by the mirror symmetryMxysince the in-plane magnetic fieldλxbreaks it and causes phase transition.The other one is that because of the phase transition between these two topological non-trivial phases, the bulk gap should be closed at a momentum away from theΓpoint; in particular, the gapless phase transition occurs whenΔt=0 and the nodal superconducting phase is protected by the chiral symmetry (see Fig.1).These results are also confirmed by the numerical calculations of the lattice model, which are presented in Appendix A.To sum up,in this section,we show that the nodal superconducting phase can be viewed as an intermediate phase between two different topological non-trivial phases;therefore the nodal structure is topologically stable and protected by the chiral symmetry.

2.3.Effects of substrate

The superconducting TSSs could be realized in the thin films of the iron-based superconductors through the molecular beam epitaxy method[71]or exfoliation;[72]in either method,the substrate will always be present.Then we shall consider if the topological nodal superconducting phase was stable in the presence of substrate.

Fig.3.The topological phase diagram of hsub (11)in the ν-λx plane withµ =0, Δ =1, and t =0.5.The red shaded area is the topological nodal superconducting phase which remains stable when the substrate exists.

A uniform substrate can be treated as a difference of chemical potential of the two surfaces;therefore we consider a termνσ0χzτzto simulate the effect of the substrate.By adding this term into the Hamiltonianhx(2),it becomes

The substrate breaks mirror symmetryMxy,but preserves chiral symmetry.We plot the phase diagram in theν-λxplane in Fig.3 with the phase boundary determined by the gap closing at theΓpoint of the above Hamiltonian.From the phase diagram,we see that the topological nodal phase is stable against the substrate.

2.4.Three-dimensional lattice model

In order to confirm the existence of the topological nodal superconducting phase and the Majorana Fermi arcs,here we construct a three-dimensional lattice model to mimic a thin film of topological insulator with superconductivity.For the normal state of an iron-based superconductor, we consider a four-band lattice model with two orbital degrees of freedom(pzand dx2-y2),[53,54]and the magnetic field is applied alongxdirection with Zeeman couplingλx,

whereσiandρiare Pauli matrices acting on spin and the orbital.vis the hopping constant which we set to unity,M(q)=M0-M1(cosqx+cosqy)-M2cosqz,withMibeing constants that control the topological phase of the normal state when the magnetic field is absent.For example,we chooseM0=-8.5,M1=-3,andM2=3,such that the normal state is a topological insulator with a band inversion atZ,and there will be one TSS on each open surface along thez-direction.[53,54]The low energy effective theory of the model Hamiltonianh3D0 (12)can also describe thek·ptheory near theΓpoint of a normal state of CuxBi2Se3where the orbital degrees of freedom come from the conduction and valence bands atΓpoint.[69]

For the superconducting part, we introduce an interorbital spin-singlet pairing term ˜Δ=Δ0iσyρxwhich is inversion-odd.The reason is that,in the effective theory(1)for the superconducting TSS, the pairing term is odd under mirror symmetryMxywhich is a remnant of the three-dimensional inversion symmetry.Then the BdG Hamiltonian reads

which is possible to be realized in the iron-based superconductors.[54,69,73]For a thin film geometry, we consider four layers along thez-direction and add an on-site energy differenceVin the top and bottom layers to simulate the effects of substrates.[54]We plot the topological band structure in Fig.4.The bulk spectra is a nodal superconductor (Fig.5(a)) and the Majorana Fermi arc exists when we choose an open boundary alongy,which is also stable against substrate potential (Fig.5(b)).The behavior of the thin film of the three-dimensional lattice model is consistent with the effective theory of the superconducting TSSs discussed in Subsection 2.1.The rich structures of the lattice model, e.g.,the emergence ofΔandΔt,will be presented in future works.

Fig.4.The BdG band spectra of the three-dimensional lattice model h3DBdG (12) with four layers along the z-direction. M0 =-8.5, M1 =-3,M2 =3, Δ0 =1.5, V =0.5 and λx =0.5.(a) Bulk spectra with qy =0.(b)Open boundary condition along the y-direction with y=30.There is a Majorana Fermi arc connecting the Majorana nodes.

3.Conclusion

In summary, we study the superconducting TSSs under an external in-plane magnetic field.Due to a pseudo timereversal symmetry,the system belongs to BDI.There exists a topological nodal superconducting phase with Majorana Fermi arcs connecting the Majorana nodes,and it is an intermediate state between two different topological chiral superconductors, which fulfills a two-dimensional superconducting analogue of Weyl semimetals.This topological nodal superconducting phase is stable against substrates, and can be realized in a three-dimensional lattice model for the thin films of an iron-based superconductor[54]as well as a topological superconductor CuxBi2Se3,[69]which can endure large in-plane magnetic field.The Majorana nodes can be controlled through external in-plane magnetic field, which may introduce a nontrivial topological Berry phase between them.[63]

Appendix A: More results on two-dimensional lattice model

The effective BdG Hamiltonian we consider for the superconducting TSSs with an external in-plane magnetic field reads

We plot the phase diagram in Fig.A1(a),and study the properties of different phases by numerics under open boundary conditions in Figs.A1(b)-A1(f).We fixt1=0.4 and varyt0.In Fig.A1(b),t0lies in the white regime of Fig.A1(a),which is a trivial gapped superconducting phase.In Fig.A1(c),t0lies in the pink regime,which is a topological nodal superconductor with a Majorana Fermi arc connecting the Majorana nodes.In Fig.A1(d),t0lies at the phase boundary between pink and blue regimes, where the Majorana Fermi arc remains and the bands touch atΓandX.In Fig.A1(e),t0lies in the blue regime,which shows the Majorana nodes atXevolve towardsΓand the ones atΓmove towardsX.In Fig.A1(f),t0lies in the orange regime,and the band gap has touched again atX.

Furthermore,we plot the phase diagram inΔt-λxplane in Fig.A2(a).We also choose five typical points in Fig.A2(a)and plot their band structures(Figs.A2(b)-A2(f)).Away fromΔt=0 line, there are chiral Majorana edge modes, and their chiralities change side ifΔthas an opposite sign.In addition,alongΔt=0,the chiral Majorana edge modes evolve into the Majorana Fermi arcs that connect the Majorana nodes.

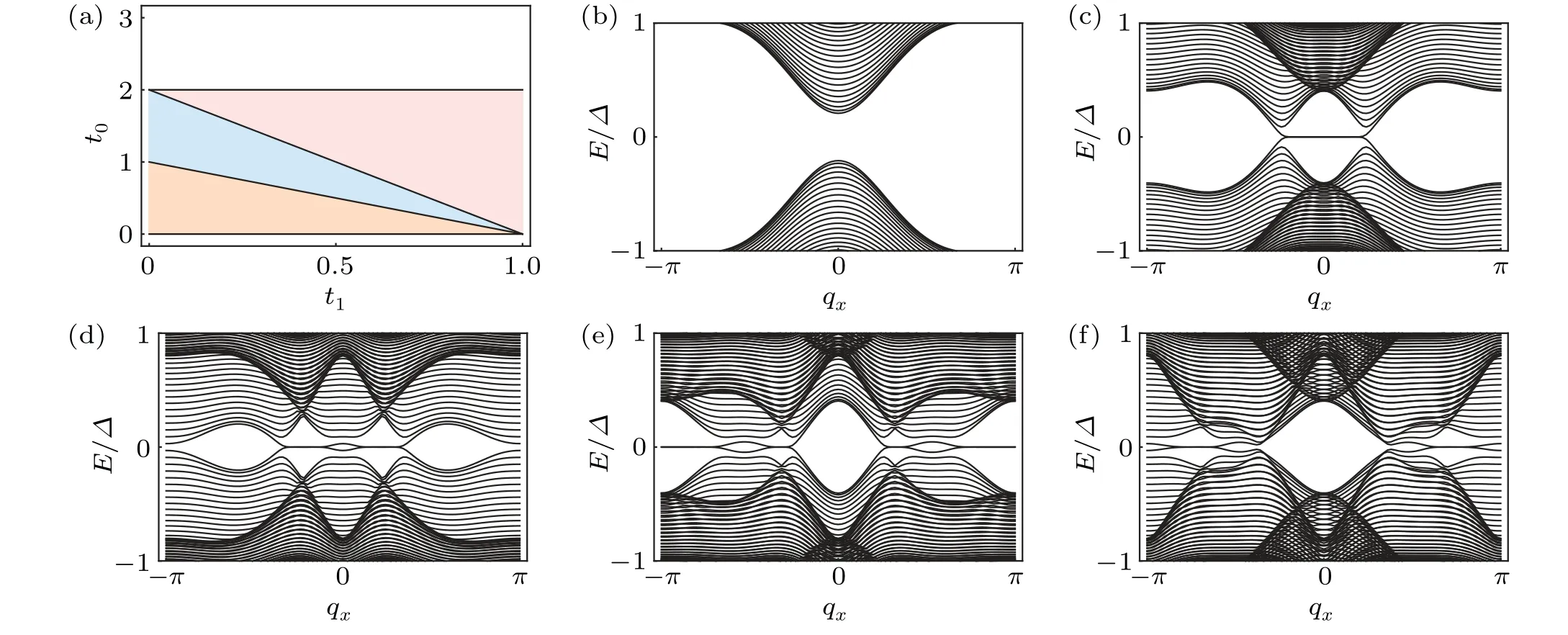
Fig.A1.(a)The topological phase diagram of the nodal superconducting phase in t1-t0 plane withµ =0,Δ =λx=1,and Δt =0.From(b)to(f)are band structures of h2D (A1)with 50 sites along the y-direction, and we fix t1 =0.4.(b)t0 =2.2, in the white regime of(a).(c)t0 =1.6 in the pink regime.(d)t0=1.2,at the phase boundary.(e)t0=0.8,in the blue regime.(f)t0=0.4,in the orange regime.

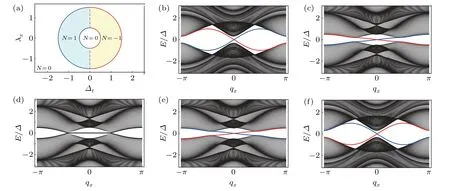
Fig.A2.(a)The topological phase diagram in the Δt-λx plane with t0 =t =0.5,t1 =1, µ =0 and Δ =1.From(b)to(f)are band structures of h2D (A1)with 50 sites along the y-direction.(b)Δt =1.2,λx=0,(c)Δt =0.2,λx=1,(d)Δt =0,λx=1,(e)Δt =-0.2,λx=1,(f)Δt =-1.2,λx=0.The red(blue)curve stands for the edge mode localizing at the left(right)edge.The chiralities of the chiral Majorana edge modes in(b)and(c)are opposite to those in(e)and(f),which is consistent with the bulk Chern number N in(a).

Acknowledgments

We thank Yue Yu and Ziqiang Wang for helpful discussions.Project supported by the National Natural Science Foundation of China(Grant Nos.11804223(MLL,YW,HZZ,HLC,TYC,XL),11474061(XL),and 12174067(XL)).