新课标视野下用PDCA复盘小学数学PBL的尝试
2023-03-12柴明智
柴明智
《义务教育数学课程标准(2022年版)》提出要选择能引发学生思考的教学方式,积极开展跨学科的主题式学习和项目式学习等综合性教学活动。结合小学六年级的“最美毕业季”活动,采用PBL的形式开展“数学助力平安校园”项目式学习,把PDCA卓越绩效管理模式循环法运用于PBL项目式学习进行新的复盘和管理,收到了良好效果。
一、项目选定
从1996年开始,每年3月最后一個星期的星期一是《全国中小学生安全教育日》。2021年的安全教育日,学校组织全校同学观看公安部和教育部联合发布的安全教育视频。其中,有一个点让孩子们印象深刻:汽车转弯时,由于内外轮走的半径不同,半径差会产生一个转弯盲区,人在其中会被车撞到,非常危险。所以,全国各大城市的道路都会在转弯处标明这个区域,学校也经常组织学生参与关于汽车“转弯盲区”的体验活动。
二、项目计划
由于放学时人杂车多,为了保证师生的安全,全国小学基本都采用校内排队等候家长接走的方式放学。这样当校门外有不安全因素时,门卫叔叔会第一时间关上大门,确保校园内的安全。如果此时同学们正在排队放学,有同学站的位置刚好是大门关上时横扫过的区域。就会导致门卫叔叔关不上门,或者被大门把同学推出校门外面。因此,我们“数学思维社”结合这个实际问题,想到可以在学校大门附近画一个类似于道路上汽车转弯盲区的区域,这样既可以把危险快速挡在门外,又能保证我们的安全。这个安全区域该如何设置呢?
三、项目实施
(一)项目开始时,通过学生小组合作,实地研究,初步提取模型
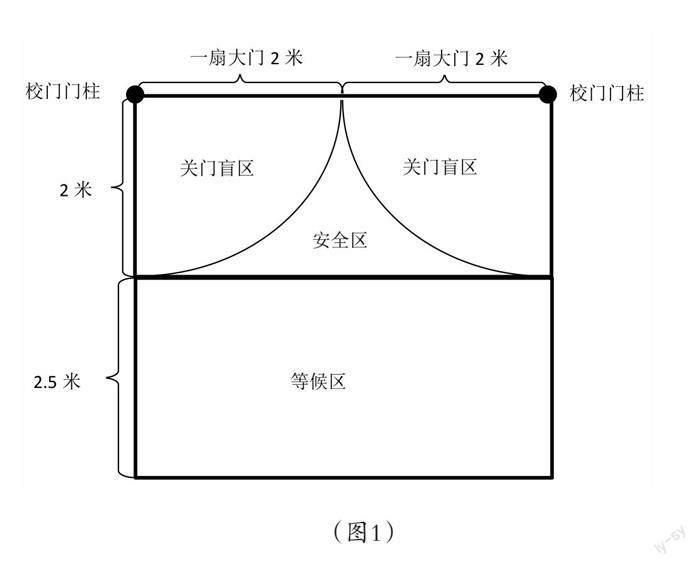
实际中当两扇大门以门柱为圆心,开关时扫过的面积,也就是关门的危险盲区。这个盲区几何直观上是两个四分之一大的圆形,两边加起来面积正好是一个二分之一的圆形。一扇大门长度作宽,乘以两扇大门长度作长,所得的长方形面积,减去关门盲区的面积,剩下部分的面积就是放学安全区域面积了。这个区域能站多少人,决定我们放学时每班队伍每行站几个人最好。(见图1)
(图1)
(二)项目实施中,学生测量研究,算出安全区
学生量得,学校一扇门的长度是2米,它可以看作是半圆的半径,这样可以算出半圆的面积等于6.28平方米。两扇大门关闭时的长度等于长方形的长,半圆的半径就是长方形的宽,长方形的面积等于8平方米。安全区的面积就用长方形的面积减去半圆的面积,等于1.72平方米。(见图1)
(三)实地回来,思考讨论划定等候区
思考:那么每个班的队伍站成几排?每行站几个人最好呢?也就是思考安全区能站多少人?我们用安全区的面积1.72平方米除以每个人大概占的0.25平方米,等于6.88人,为确保安全,我们使用“去尾法”取整,所以安全区能站6人。由此我们得到每个班排成:每行6人最安全。平均每班约有46人左右,除安全区已经站好的6人(第1排学生),还剩40人左右,每人占0.25平方米,一共还需要一个10平方米的等候区。等候区的长等于两扇大门关闭时的长度,就是4米,那么等候区需要的宽就是2.5米。(见图1)
四、项目成果展示
通过以上三大模块的研究,我们可以知道:在任何一所学校,只需量出一扇大门的长度就能得出以下结论(以云南师范大学附属小学金安校区高段为例):
(一)每次出门6人最为安全,也最为合适;
(二)可以在校门内画出:关门盲区、安全区和等候区三大区域,引导同学们放学。
最后,我们还在解决问题过程中,推理并得出了一个理想的数学模型:每个班队伍每行人数等于1.72乘一扇大门宽度的平方。所以只要量出一扇大门的宽度,就可以利用我们的模型得到每班的队伍每行站几人最合适。
五、项目评价
(一)优点
1.用PDCA循环法,对PBL学习的核心元素,进行准确科学的分析研究。可以更加准确,更加有效地实施项目式学习。
2.以此次学习为例:对学生的几何直观,空间观念,推理能力,推理意识培养比较突出。
(二)可以改进的地方
1.在项目计划环节缺少社会协助,可以邀请交通研究方面专家介绍:道路上的汽车转弯盲区是怎么样规划出来的。
2.在项目实施环节中老师可以教学一下,有关“数学建模”的知识,使我们有模型意识,建立的模型更加精准,这样才符合新课标培养学生有模型意识的要求。
3.在项目展示环节,我们可以对建立的数学模型用电子计算机进行模拟演示。这样符合新课标核心素养中创新和抽象能力的培养。
六、项目反思
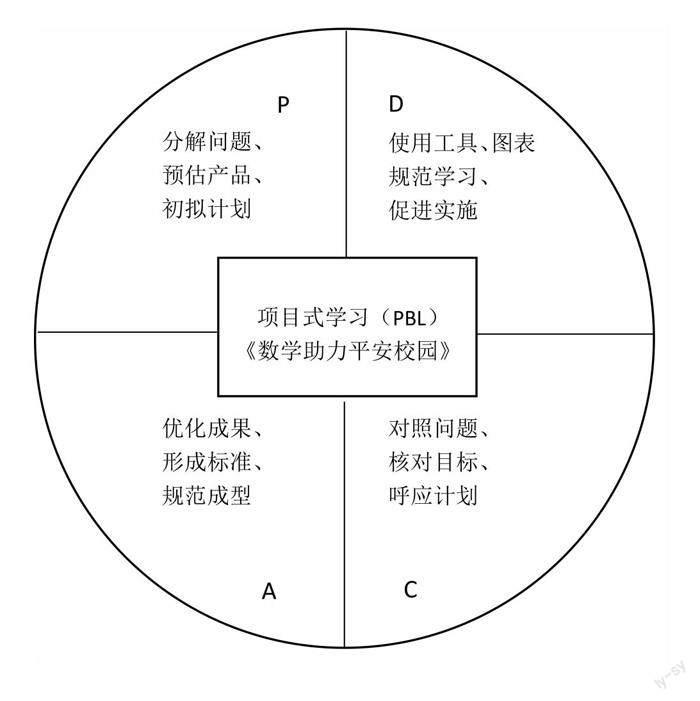
(一)在项目计划时(P环节),我们要依据课标新要求紧扣核心素养进行设置,结合小学数学教学内容具体年段课程的要求。认真分析学生学情、基础知识、基本能力;分析学生掌握的各学科综合情况。
(二)在项目实施中(D环节),我们要加强同学之间的合作探究,整合各种资源,进行有效的教师引导,提供必要的社会协助。
(三)在项目成果审视中(C环节),我们可以把项目研究取得的成果,有效地呈现出来,积极的展示。
(四)在项目改进创新中(A环节),我们要作出详细的规范的评价记录,并带领学生讨论交流,对项目进行复盘,对项目进行改进创新,二次管理。
【注:本文系云南省教育科学规划基础教育专项项目《义务教育课程标准实施难点突破之基于PDCA循环法的小学数学项目式学习优化研究》(BFJC22025);昆明市教育科学研究“十四五”规划课题《基于PDCA循环法的小学数学项目式学习研究》(JY202205)】
