基于WTLS 的倾斜摄影模型坐标变换方法

钱荣荣，张 畅，龙 容，余 航

（1.浙江省测绘科学技术研究院，浙江 杭州 310012；2.苏州科技大学，江苏 苏州 215000）

近年来，无人机倾斜摄影测量技术发展迅速，倾斜摄影测量数据能够反映地物的实景三维模型，获取建筑物等地物细节信息，为城市三维规划提供数据支撑和辅助决策支持[1]。目前各规划部门多采用的地方坐标系，为了更好地进行规划服务，需进行倾斜模型三维数据与地方坐标系之间的三维坐标转换工作。

为了得到三维坐标转换模型参数最佳值，通常采用最小二乘（LS）方法，建立经典的高斯-马尔科夫模型对误差方程进行求解，但该方法通常假设坐标已知值不受偶然误差污染，随机误差仅存在观测向量当中。但实际情况中，同一控制点的两套坐标量测值均存在偶然误差，因而最小二乘法在该情况中存在一定的局限性。为了同时考虑两方面的误差影响，本文引入加权总体最小二乘（WTLS）方法来解算三维坐标转换参数，同时结合计算机图形学和场景渲染技术，借助目前主流的C++编程语言和独立于硬件的开源三维图形渲染引擎（OSG）实现倾斜摄影测量模型结构数据解析，进行三维坐标转换。

1 坐标系统转换模型

设有两个坐标系A和B，A为源平面坐标系，B为目标平面坐标系（如图1所示）。某点P在A坐标系下的空间直角坐标为[xAyA]T，设该点在B坐标系中的空间直角坐标为[xByB]T，其中[x0y0]T为A坐标系转换到B 坐标系的平移参数，k为A 坐标系转换到B坐标系的尺度因子。

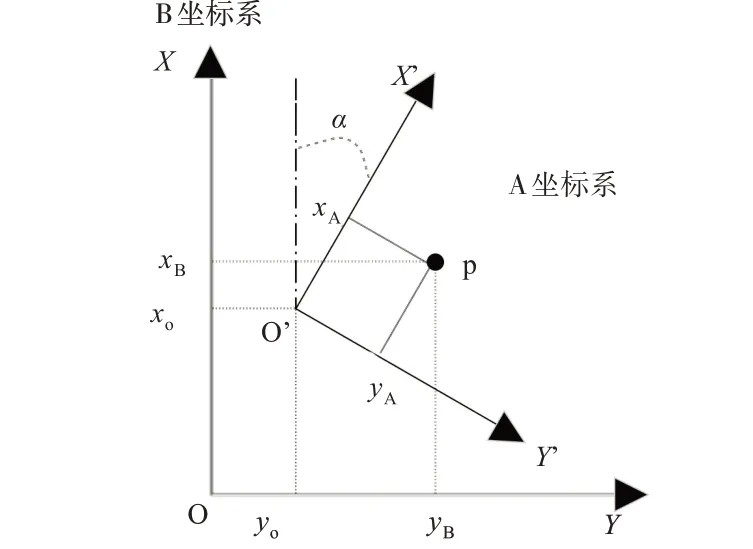
图1 不同平面坐标系

则平面四参数的转换模型为：

2 参数模型求解

2.1 最小二乘解

当观测个数w（w=2×n）大于参数个数t时，以往的做法是采用最小二乘方法求得参数的最或然值。此时需要有一个基本假设，即偶然误差只存在于观测向量L中，而系数矩阵A是完全正确且不受偶然误差污染。因此观测值方程可表示为:

2.2 加权总体最小二乘解

在转换模型中源坐标数据是含有误差的，但经典最小二乘仅考虑观测值L的误差，如公式（4）所示，而认为系数矩阵A不含误差。在实际工程应用中，两个坐标系下测量得到的公共点坐标都是存在误差的，需考虑系数矩阵和观测值矩阵同时存在偶然误差的情形，同时对系数矩阵和观测值矩阵进行改正[2]。

以平面坐标转换为例，其中,PA可根据公式（11）依据协因数传播定律求解。

加权总体最小二乘估计准则为：

通过迭代求解参数的WTLS 估计，进行精度评定，该算法的迭代过程为[3]:

计算加权最小二乘解作为迭代初始值：

3 实验分析

3.1 模拟数据

为了比较WTLS与LS不同算法对坐标转换的精度的影响，采用设计参数与模拟数据对不同算法进行解算[4-5]，其中13 个控制点的平面坐标(x前，y前)与点位如表1 所示，假设模型转换的4 个参数分别为：平移参数a=1 ，b=5；旋转参数α=0.708 626 27；尺度比参数μ=0.921 954 45，转换后的控制点平面坐标(x后，y后)与点位见表1和图2。

图2 转换前后控制点点位

表1 控制点在转换前、后的平面坐标及相应权值

为比较应用不同算法实现坐标对点位精度和转换参数精度的影响，分别对控制点已知坐标和观测坐标加入数值不等的误差，并设点位权值。加入误差后的控制点坐标(x′，y′)见表2。

表2 加入误差的控制点坐标及权值

应用加入误差的控制点坐标，分别使用LS 和WTLS，其中WTLS 迭代阈值ε设置为10-12，求解转换参数并与真实值进行对比（表3）。结果表明，WTLS在顾及转换模型的系数矩阵误差的同时（表4），求解得到的参数值更接近真实值。根据转换参数计算各控制点转换后的坐标值与真实值的差值，得到转换坐标差异RMS值方面WTLS也优于LS。

表3 不同算法求解的转换参数比较

表4 观测值中的残差计算值

3.2 倾斜摄影测量

倾斜摄影测量数据模型是由网格面模型经过纹理映射构成真实三维模型，利用不同视角的网格面片将三维模型表现。通过高密度三维点云，构建城市3D TIN 数字表面模型[6]，该模型与建筑物的特征点、线、面相对应，构网算法复杂，每个三角形面片的顶点、边和面间关系表达场景离散点拓扑关系，反映场景可视化效果，获取城市真三维模型成果。

根据倾斜模型数据结构特点，借助OSG场景中自顶向下的分层树状数据结构来组织倾斜摄影测量空间数据集，处于场景树底部的叶子节点包含了倾斜场景对象的实际几何信息[7]，通过计算得到的转换模型参数对叶子节点进行坐标转换。

为了测试转换效果，以某区域通过Smart3DCapture 软件生产的倾斜摄影测量数据为例进行转换工作，该区域的倾斜数据模型如图3 所示。其中图3a为模型真实三维模型效果，图3b 为模型的三角网结构数据，图3c 为模型的点云数据。该区域高程方面需配合似大地水准面精化[8]成果综合考虑，因此本文只针对模型平面位置进行转换处理，高程方面维持原有模型数据不变。已知该区域在当地坐标系和CGCS2000 坐标系下的已知公共点共36 个，其中部分数据如表5 所示，求取CGCS2000 坐标系到当地坐标系下的转换参数。

图3 某区域倾斜摄影测量数据模型

表5 CGCS2000坐标系和地方坐标系下公共点坐标

分别通过最小二乘和加权总体最小二乘计算转换参数，其中WTLS 迭代阈值ε设置为10-8，为了方便进行检核，计算控制点经转换后的坐标与真值之间的差异RMS 如表6 所示。可以看出，WTLS 的转换效果一定程度上优于LS，同时WTLS考虑系数矩阵A中部分观测元素的误差，理论上更加严密。

表6 不同算法求解效果比较

在得到精确转换参数的基础上，借助OSG自定义InfoVisitor 类，继承自osgNodeVisitor 并应用于节点访问的方法，重构apply()虚函数。获取关联的倾斜模型数据节点通过accept()方法调用访问器，访问器通过apply()方法获取传入的节点对象，并执行倾斜数据节点在位置变换中所需的操作。

将转换后的倾斜模型数据加载到超图平台[9]进行显示，并与周边的二维数据进行套合，结果如下图4，可以看出转换后模型套合情况良好，模型完整性良好，杜绝了可能出现的漏面、拉花等现象。

图4 转换后倾斜模型

4 结 语

转换参数计算方面，本文考虑到两套坐标系观测值中均存在偶然误差影响，属于变量含误差模型，在最小二乘的基础上，引用加权总体最小二乘算法计算转换模型参数。分析表明利用WTLS 求解模型转换参数，相较于LS方法，一定程度上提高了转换参数的求解精度。因三维数据结构描述复杂、计算复杂度高等不足，三维地理空间数据的空间参考难以统一。设计实现了以三维数据要素、图案、点集为核心的倾斜三维模型的数据结构解析工作，并将其应用于坐标转换当中，取得了一定的效果。