撕碎机刀片的疲劳寿命分析

徐志鹏

（江苏建筑职业技术学院智能制造学院，江苏 徐州）

引言

作为撕碎废弃材料的常用机械设备，撕碎机通常用于处理未经加工的边角余料或废弃的原材料，从而使得其体积更加微小[1]。

国内学者对于机械设备疲劳寿命分析进行了大量的研究工作。胡海明[2]利用CAE及疲劳分析软件对弓型座进行了应力、位移与疲劳寿命分析，确定了最大等效应力的位置与方向，计算出了最低疲劳寿命点，并对延长疲劳寿命提出了建议。樊俊玲[3]基于传统的疲劳实验数据，利用概率统计分析的方法，预测了不同存活率下的疲劳应力- 寿命曲线，结果表明其预测的结果与传统实验分析的结果具有良好的相关性。

然而，对于撕碎机刀片的疲劳寿命分析却鲜有报道。因此，基于以上学者的研究基础，本研究建立撕碎机刀片的有限元模型，仿真得到应力应变云图以及疲劳敏感性图，利用常用材料的参数值拟合得到撕碎机刀片的P-S-N 曲线，分析不同存活率下的疲劳- 应力曲线，并结合Miner 理论计算出撕碎机刀片的最大使用寿命。

1 撕碎机刀片疲劳寿命有限元分析

1.1 问题分析

如图1 所示为一种双轴撕碎机，本研究主要对其刀片的疲劳寿命进行分析。本研究所研究刀片的主要结构参数为：刀片外径100 mm，刀片厚度18 mm；材料为Q235 普通碳素结构钢。根据撕碎机刀片在实际工作过程中的受力情况，在不影响计算结果情况下，本研究对撕碎机刀片的受力模型进行了简化。施加在刀面上的应力为20 MPa，疲劳强度因子为0.8。由于刀片在工作过程中受非恒定载荷影响，刀片材料结构钢为韧性材料，因此本研究采用Goodman 理论修正平均应力[4]。

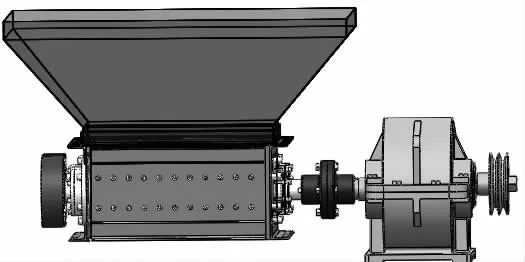
图1 双轴撕碎机三维模型

1.2 参数设定

本研究利用SolidWorks 软件建立撕碎机刀片的物理模型，并将其导入到ANSYS Workbench 软件中进行疲劳寿命分析。如图2 所示，设置有限元网格质量为最好，网格形式为四面体网格，得到网格节点总数为180 280 个，单元数为43 826，单元大小为2 mm。其弹性模量为2×1011Pa，密度为7 850 kg/m3，泊松比为0.3。

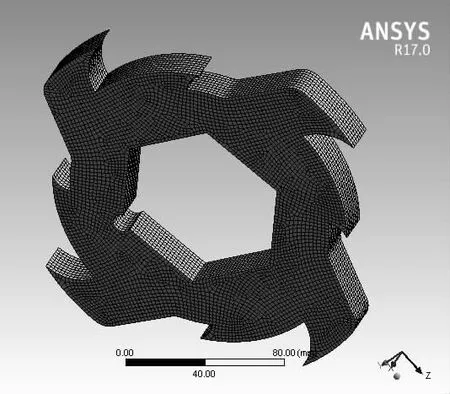
图2 撕碎机刀片有限元网格模型

1.3 撕碎机刀片应力和应变分析

为了更好地观察撕碎机刀片在随机载荷工况下的疲劳敏感曲线变化情况，加载了如图3 所示的随机载荷并进行求解。

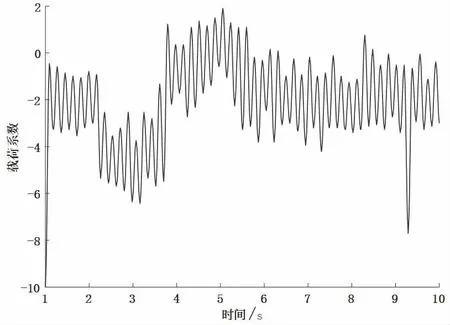
图3 随机载荷

求解得到的撕碎机刀片等效应力分布情况。其中，可以明显地看出最大等效应力位于刀刃处，其值为241.34 MPa；同时最大应变也位于刀刃处，其值为0.0081572。

1.4 撕碎机刀片疲劳寿命敏感性分析

刀具的安全载荷幅度范围是0%～90%，寿命次数保持1×107次；当载荷变化幅度大于90%时，撕碎机刀片疲劳寿命急剧下降，尤其当载荷变化幅度为150%时，其寿命次数接近于零。

2 撕碎机刀片的疲劳寿命P-S-N 曲线

2.1 模型建立

由上述的有限元模型分析结果可知，撕碎机刀片最大疲劳寿命为1×107次，远大于104，属于高周疲劳。对于此种应力循环水平较低且应力变化相对较大的高周疲劳，以往研究中大多使用S-N 曲线来定量分析疲劳寿命。然而，S-N 曲线一般都是取疲劳试验的平均值绘制出来的，而实际的疲劳样件往往受不稳定的载荷、被试件的表面粗糙度、加工误差等因素的影响，从而导致测出的试验数据具有分散性[5]，并且这种分散特点通常与存活率有关。因此，本研究利用P-S-N 曲线分析撕碎机刀片的疲劳寿命。当用双对数坐标来表示应力与寿命的关系，则其方程可表示为：

式中：σ 为应力均值；Np为存活率为p 时的寿命；ap和bp为材料常数值。

2.2 参数设定

依据文献[6]中通过实验测得的材料常数，查得Q235 普通碳素结构钢在旋转弯曲载荷下的材料常数，其数值见表1。

表1 P-S-N 曲线的参数值

2.3 结果分析

存活率P 为99.9%时，疲劳应力最低，P 为50%时，疲劳应力水平最高。值得注意的是各个存活率下的疲劳应力达到400 MPa 时，疲劳寿命均趋近于零，这是由于此时所施加的应力接近材料的抗拉强度460 MPa, 撕碎机刀片不满足静强度，发生了瞬时断裂。

3 基于Miner 理论的撕碎机刀片疲劳寿命预测

零件受到各种扰动载荷的作用，会产生一定程度的损伤，并且随着损伤不断地叠加，当零件损伤达到所能承受的最大值时就会发生疲劳断裂，这种现象被称为疲劳累积损伤理论[7]。工程实践中通常使用Miner理论对线性累积损伤进行分析[8]，它的一般分析计算步骤见图4。

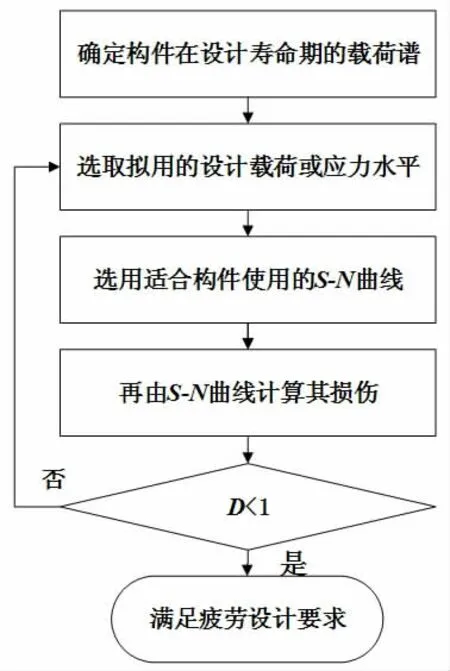
图4 Miner 理论分析步骤

结合上述的P-S-N 曲线，取存活率P 为99.9%时的参数值，带入式（3）可得：

根据Q235 最大的抗拉强度460 MPa，以及有限元仿真得到的安全载荷疲劳变化幅度范围，取载荷P为300 MPa，依次将0.8 P, 0.7 P, 0.6 P 带入式（4）中，即可得到表2 所示的不同载荷水平下的疲劳损伤值，其中的总损伤D 由公式（5）计算。依据图4 的分析步骤可知当D＜1 时满足疲劳使用要求，如D＞1 则要重设载荷谱，直至达到使用要求。

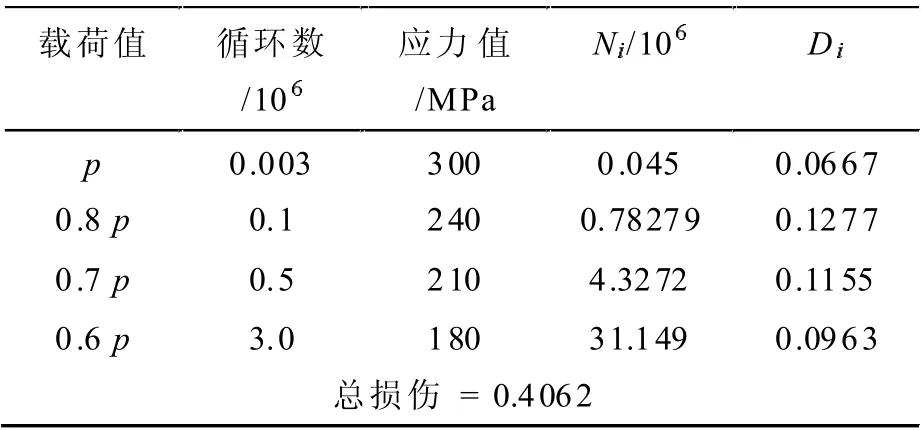
表2 损伤计算

如将刀片的总损伤看作为一个循环体，那么整个寿命由λ 个循环体组成，即：

根据Miner 理论，发生疲劳断裂的临界条件应为D=1，故由式（6）可得：

λ=1/0.4062=2.4618 年

4 结论

（1） 建立了撕碎机刀片的SolidWorks 三维模型和基于Workbench 的有限元模型。结果表明，撕碎机刀片刀刃位置存在应力集中，当施加的载荷变化幅度范围大约为0%～90%时，寿命次数达到1×107次。

（2） 建立了撕碎机刀片疲劳寿命的P-S-N 曲线模型，仿真得出不同存活率下的疲劳寿命- 应力曲线。结果表明，随着存活率的不断增加，同一寿命下的应力水平将会随之降低。

（3） 结合Miner 理论，利用所得到的P-S-N 曲线，根据有限元仿真得到的最大应力，设定寿命期内的载荷谱。并在此工况下，计算得出该撕碎机刀片使用寿命最大可达2.4618 年。