基于干扰观测器的机械臂自适应模糊滑模控制

李 虎 刘泓滨

（昆明理工大学机电工程学院，云南 昆明 650500）

随着工业技术的发展，机械臂凭借着在工作空间中快速、稳定和高效的工作特点，被广泛地使用在工业自动化生产过程中，例如焊接、搬运、喷漆、码垛和机械加工等方面[1]。实际应用表明，为了提高工业生产和制造效率，对机械臂高精度的轨迹跟踪控制尤为重要。

机械臂的轨迹跟踪控制是对机械臂各关节的轨迹进行控制，使机械臂能够以较好的动态性能跟踪期望的轨迹[2]。由于机械臂轨迹跟踪控制很容易受到许多不确定因素的干扰，所以采用传统的控制方法很难满足机械臂轨迹跟踪控制的精度要求。相比之下，滑模控制可以有效降低不确定因素的干扰和机械臂内部参数变化的影响，具有较强的抗干扰性，因此在机械臂轨迹跟踪控制中采用滑模控制是一种十分有效的方法。但是在实际应用中，传统的滑模控制存在抖振的问题，即运动轨迹高频地穿梭在滑模面两侧。近年来，已有大批的国内外专家和学者在围绕机械臂轨迹跟踪控制等方面展开了大量的研究和探讨。张国山等人针对传统趋近律存在收敛速度缓慢和抖振的问题，采用了一种新型趋近律的滑模控制方法，通过引入新型函数对传统的幂次趋近律进行改进，该方法不仅提高了系统的跟踪速度而且还减小了系统的抖振[3]。周名侦等人在非线性滑模控制的基础采用干扰观测器对可观测的扰动进行力矩补偿，并通过仿真与非线性滑模控制和传统滑模控制相比较，进一步地提高了机械臂轨迹跟踪的精度[4]。张润梅等人为了减小机械臂建模误差和外界干扰给轨迹跟踪带来的影响，分别采用于干扰观测器和自适应率对复合干扰进行估计补偿，有效地克服了建模误差和外界干扰的影响[5]。文献[6]针对系统扰动和不确定性干扰，采用径向基神经网络进行估计，并提出了积分全阶终端滑模控制，加快了系统的收敛速度。崔鑫等人针对滑模控制的抖振问题，在滑模控制的基础上引入模糊控制，利用模糊控制对切换增益进行模糊化，有效地减小了系统的抖振和外界非线性干扰的影响[7]。倪骁骅等人针对机械臂在工作过程中存在许多不确定因素的影响，提出了一种基于模糊补偿的滑模变结构控制方法，利用模糊系统的万能逼近原理对系统的不确定性误差和干扰进行逼近，能够较好地改善机械臂轨迹跟踪性能[8]。邹思凡等人为了解决机械臂各关节位置跟踪控制中的抖振等问题，对非线性干扰观测器进行了改进，并使用反演自适应滑模控制对无法观测的扰动进行估计，该控制策略不仅可以减小机械臂系统的抖振，而且还提高了轨迹跟踪的精度和速度[9]。

综上所述，在机械臂轨迹跟踪控制中，不确定性干扰和滑模控制固有的抖振等问题一直是研究者们致力于解决的重要问题。针对这些问题本文提出一种基于干扰观测器的机械臂自适应模糊滑模控制策略。首先，使用新型趋近律来减小机械臂滑模控制系统中抖振的影响；其次，采用干扰观测器对机械臂建模误差和外界干扰进行估计，根据干扰观测器的观测值对机械臂的输入力矩进行补偿；最后，对于无法观测的部分，采用模糊逼近原理对未知的扰动进行估计，进一步提高机械臂的轨迹跟踪性能。

1 多关节机械臂动力学建模

本文在建立多关节机械臂的动力学模型时，采用的是拉格朗日动力学的方法具体表达式如式（1）所示。

式中：M(q)为机械臂正定质量矩阵；C(q,)为离心力和哥氏矩阵；G(q)为重力矢量；q、分别是机械臂关节的位置、角速度和角加速度；T为机械臂控制力矩；d为外界干扰，包括建模误差、参数变化、各关节摩擦力矩和不确定性干扰等。

2 滑模控制器设计

机械臂是一个非线性、强耦合和时变不确定的系统，所以采用传统的滑模控制策略满足不了机械臂轨迹跟踪控制的精度和速度要求。为此，在控制器的具体设计中，把可以观测的干扰和不可以观测的干扰分为两个部分，对于两个部分的干扰分别采用干扰观测器和模糊系统的万能逼近原理进行力矩补偿。机械臂系统的控制结构如图1所示。

图1 机械臂系统的控制结构

2.1 干扰观测器的设计

针对机械臂控制系统中存在复合干扰的问题，采用非线性干扰观测器对干扰值进行估计并将估计值作为反馈信号来调节系统控制力矩，以减小复合干扰对机械臂系统的影响，使系统表现出较强的抗干扰性。

因此干扰d由式(1)可知：

式中：dˆ是d的估计值，则干扰的估计误差F定义为

则干扰观测可初步设定为

式中：L(q,)是干扰观测器中待设计的增益矩阵。

由式（6）可知，通过设计适当的增益矩阵，可以使观测误差呈指数收敛。但是在机械臂实际跟踪控制中，机械臂各关节的加速度信号一般很难获取，所以实现上述观测器较为困难，因此还需要对非线性干扰观测器进一步设计。

为了实现上述观测器，定义辅助向量为

式中：z∈R2；p(q,)是待设计的非线性函数。同时增益矩阵L(q,)和非线性函数p(q,)应满足以下条件：

通过式（7）和式（8）可得：

结合式(2)～(9)可得：

因此可得干扰观测器为

使用干扰观测器后，机械臂系统复合扰动由d变成了F，则机械臂动力学模型为以下形式：

2.2 滑模控制器的设计

滑模控制作为非线性控制的方法之一，其非线性是指系统控制的不连续性，根据被控系统的当前状态不断地发生改变[10]。由于外部干扰和系统自身参数的变化对滑动模态影响较小，这使得滑模控制具有较强的抗干扰性和鲁棒性。

定义qd是 机械臂的期望轨迹，e=q(t)−qd(t)是轨迹跟踪误差函数，则取滑模面为：

式中：Λ=diag{Λ1,Λ2,···,Λn}(Λn>0)。当t→∞时，轨迹跟踪误差呈指数收敛，Λ值越大，跟踪误差收敛越迅速。通过合理的设计对角矩阵Λ，可使得机械臂系统有较好的动态性能[11]。由式(12)和(13)可得：

滑模变结构控制具有较强的抗干扰性和鲁棒性，但存在固有的抖振问题，系统的抖振是无法被完全消除的，但可以通过一些有效的方法削弱系统存在的抖振。本文采用了改进型的指数趋近律来削弱滑模控制带来的抖振，新型趋近律的表达形式如下：

式中：k1>0；k2>0；α>0；tanh(s)为双曲正切函数。

稳定性验证，取Lyapunov函数为

由式(15)和(16)可得：

由式(17)可知，该新型趋近律满足Lyapunov稳定性理论且控制系统为渐进稳定。

由式(14)和(15)可得系统的控制率为

3 自适应模糊滑模控制器设计

在实际工作环境中，机械臂系统受到的外界干扰d由许多复杂的因素耦合而成，外界干扰d的上界值通常情况下很难预测，因此，在设计系统的控制器时，应该尽量避开d的上界值。在上文控制器的基础上，为了减小外界扰动的影响，引入模糊逼近的方法来估计外界干扰信号d中无法利用干扰观测器观测出来的部分。

3.1 模糊控制系统设计

若模糊逻辑系统使用单值模糊化，乘积推理机和重心平均解模糊化，则模糊逻辑系统的输出可由下式表达[12]：

式中：θ为可调参数向量且θ=[θ1,···,θm,···,θM]T；ξ(x)为模糊基函数向量且 ξ(x)=[ξ1(x),···,ξm(x),···,ξM(x)]T；M为模糊规则数量；µm(xi)为模糊集合m的隶属度函数 。

3.2 自适应控制率设计

为了减少模糊规则的总数，本文使用模糊系统来 逼近无法观测的摩擦干扰函数F(),则模糊系统可设计为

自适应模糊滑模控制率可设计为

只要合理地选取k1和k2的值，当逼近误差 ω很小时，可保证≤0。当≡0时，s≡0，根据LaSalle不变性原理[13]，该系统为渐进稳定。

4 仿真分析

本文以二自由度串联机械臂为例，机械臂动力学模型式（1）中各个矩阵参数为：

式中：p=(m1+m2)l12。

在Matlab/Simulink中建立机械臂的动力学模型并进行仿真，仿真中各参数可设置为：m1=0.5kg、m2=1.5kg分 别为机械臂两连杆的质量；l1=1m、l2=0.8m分别为两连杆的长度；q1、q1分别为两连杆实际轨迹，初始轨迹为期望轨迹为在仿真中只考虑粘性摩擦和库仑摩擦其中z=0.5、l=0.1；新型趋近律中的参数k1=dig[10,10]，α=1.8k2=dig[50,50]；在干扰观测器中：

在模糊逼近中隶属度函数为：

由图2和图3曲线可知，在不确定干扰的情况下分别采用传统趋近律滑模控制和新型趋近律滑模控制对机械臂1、2关节位置进行轨迹跟踪控制，传统的滑模控制策略相较于新型趋近律滑模控制策略存在明显的抖振且跟踪精度低等问题。由图3和图4曲线可知，在新型趋近律滑模控制策略下采用非线性干扰观测器对新型趋近律的滑模控制策略进行补偿以减小外界扰动的影响，干扰观测器可以有效地改善系统的跟踪性能。有图4和图5曲线可知，采用模糊逼近的方法来估计系统中无法观测的扰动，可以进一步提高了系统的跟踪性能。图6为机械臂1、2关节位置的轨迹跟踪误差曲线，图7为模糊补偿的变化曲线。

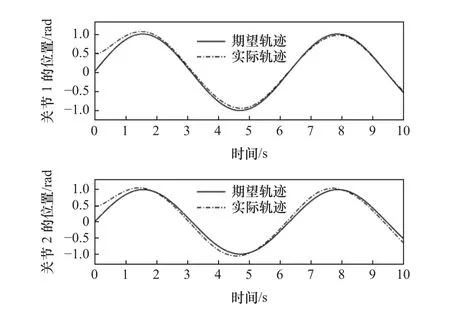
图2 传统趋近律轨迹跟踪曲线

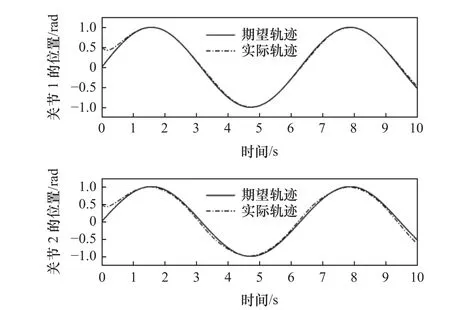
图3 新型趋近律轨迹跟踪曲线

图4 新型趋近律轨迹跟踪曲线（含干扰观测器）

图5 本文的控制方法的轨迹跟踪曲线

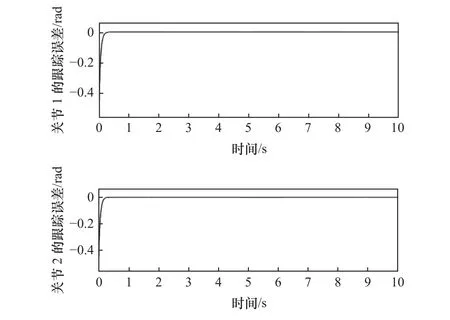
图6 本文控制方法的轨迹跟踪误差曲线

图7 模糊补偿的变化曲线

由表1可知，在传统滑模控制策略下机械臂的1、2关节轨迹跟踪存在明显的抖振和误差且最大误差分别为0.071 7 rad和0.122 4 rad；而在新型趋近律滑模控制策略下机械臂双关节的最大跟踪误差为0.035 5 rad和0.109 5 rad，由此可以说明新型趋近律滑模控制策略可以有效地削弱机械臂系统的抖振，提高轨迹跟踪的精度。在新型趋近律的基础上加入干扰观测器，机械臂1、2关节分别在0.49 s和0.74 s后能够较准确地跟踪期望的轨迹且最大跟踪误差分别为0.026 8 rad和0.060 7 rad。采用本文的控制策略机械臂1、2关节在0.2 s时能够稳定跟踪机械臂的期望轨迹且最大跟踪误差为0.003 8 rad和0.004 1 rad，具有较快的收敛速度和较高的跟踪精度。

表1 不同方法的仿真数据对比

5 结语

为了验证本文控制策略可行性和有效性，首先，采用传统趋近律滑模控制与新型趋近律滑模控制进行仿真试验比较，来证明新型趋近律可以有效地削弱系统的抖振；其次，在存在外界干扰的情况下使用新型趋近律滑模控制进行仿真，并且使用干扰观测器对机械臂系统的复合干扰进行估计补偿，验证了干扰观测器可以提高系统的跟踪性能；最后，在存在外界干扰的情况下采用新型趋近律滑模控制，并同时采用干扰观测器和模糊补偿的方法进行仿真，结果表明模糊补偿可以进一步地改善系统的跟踪性能。通过以上仿真结果表明，基于干扰观测器的机械臂自适应模糊滑模控制策略可以有效地提高机械臂轨迹跟踪的精度，进而证明了该方法的有效性和准确性。