电磁直线执行器变论域双模糊自抗扰控制＊

李德同 葛文庆 谭 草 陈杰炜 鲁应涛 李晓晨

（山东理工大学交通与车辆工程学院，山东 淄博 255049）

相比于传统的伺服电机驱动装置，电磁直线执行器精简了机械结构，取消了运动转换机构，因而具有高效节能、结构紧凑和响应迅速等优势，被广泛应用于汽车、航空航天及现代机床等领域。但由于取消了中间传动环节，导致内外部不确定扰动直接作用于电磁直线执行器上，这就给控制器的设计带来了极大的挑战[1]。

近年来，众多先进算法的应用提高了执行器的控制性能，如滑模控制、自适应控制、鲁棒控制、最优控制和智能控制等。文献[2]中提出了一种音圈电机滑模-自抗扰控制方法，通过设计外位置环模态选择方法，远离滑模面时采用滑模控制实现快速响应，到达滑模面时采用自抗扰控制消除抖振，提高了系统的稳定性和控制精度。文献[3]中提出了一种基于压力补偿的双闭环自适应鲁棒控制方法，用以克服外界干扰对电磁直线执行器运动的影响，应用在电磁驱动排气门机构上取得了良好的应用效果。文献[4]中提出了一种时间最优点位远动控制技术，将双积分系统的时间最优控制与扩张状态观测器结合，并采用了特殊的非线性函数对时间最优控制的抖振现象进行了改进。文献[5]提出了一种基于遗传算法的自抗扰控制策略，采用遗传算法对控制器参数进行寻优，提高了控制系统的跟踪性能和抗干扰能力。

自抗扰控制器能够将系统的内外部扰动都归结为总和扰动，并通过观测器对其进行观测补偿，具有较强的鲁棒性。但是，传统ADRC中需要调整的参数众多，整定过程复杂，为了方便工程应用和简化参数整定过程，本文提出了一种变论域双模糊的控制方法对自抗扰参数进行在线自整定。

1 电磁直线执行器数学模型

电磁直线执行器采用Halbach永磁阵列增加间隙中的磁场强度[6]，两个线圈绕组的电流方向相反以减小电枢反应，具有功率密度高、响应迅速等优势。其结构示意图如图1所示，详细工作原理见文献[7]。

电磁直线执行器是一个复杂的机电磁耦合系统，因此需要分别对电路子系统、磁路子系统与机械子系统建立数学模型。由于摩擦力的非线性特性，本文采用的一种改进的LuGre动态摩擦力模型[8]。综上，可得电磁直线执行器的状态空间方程为

式中：U为电源电压；R为整个线圈的电阻；L为整个线圈产生的电感；I为通过线圈的电流；v为线圈动子的运动速度；Ke为反电动势系数；Km为电磁力系数；M为电机动子的质量；x为动子的位移；Ff为摩擦力；c为阻尼系数。

2 控制系统设计

电磁直线执行器控制系统采用了内电流环PI控制、外位置环变论域双模糊自抗扰控制的双闭环控制。内电流环采用PI控制，可以使电流响应迅速，无超调，稳态无误差。而位置环采用变论域双模糊自抗扰控制方法，可以实现自抗扰控制中关键参数的自适应，第二级模糊控制调节自抗扰控制中的关键参数，第一级模糊控制可根据输入误差的大小实时调整第二级模糊控制的输出论域，从而使得模糊控制具有自适应性，提高控制系统的稳定性和抗干扰能力。系统结构框图如图2所示。

图2 变论域双模糊自抗扰控制

2.1 自抗扰控制器(ADRC)

自抗扰控制器的基本结构如图3所示，包括3部分：跟踪微分器(TD)、扩张状态观测器(ESO)以及非线性状态误差反馈(NLSEF)。

图3 自抗扰控制框图

2.1.1 跟踪微分器设计

当输入目标值为突变信号时，系统由于惯性不可能产生突变，容易在控制前期产生超调。跟踪微分器可以为目标值安排合适的过渡过程并给出微分信号[9]，能够有效地减少超调现象，提高控制性能。其离散形式为

式中：h为积分步长；r、h0为跟踪微分器参数；fhan(y1(k)−yt(k),y2(k),r,h0)为最速控制综合函数，记fsg(x,d)=(sign(x+d)−sign(x−d))/2，即可得将fhan(y1(k)−yt(k),y2(k),r,h0)表示为式（3）。

式（3）中：h为积分步长，r、h0为跟踪微分器可调参数

2.1.2 扩张状态观测器设计

扩张状态观测器借用状态观测器的思想，把能够影响被控输出的总和扰动扩张成新的状态变量，并利用被控对象的输入输出数据对其估计[10]。

将电磁直线执行器模型简化为一个二阶系统[11]，将数学模型化为状态方程

式中：x1为 动子端位移；x2为动子端速度；u为控制量，并令

式中：f(x,v,ω)为 系统内外扰动总和；Fd(ω)为外界环境的不确定性干扰项。把总扰动f(x,v,ω)扩张成新的状态变量x3同时令x˙3=ω(t)，控制量u=u0−z3/b，则可将系统模型扩张成积分串联型系统

针对上述系统模型，一般扩张状态观测器的离散形式可设计为

式中：h为积分步长；k为第k个采样时刻；z1、z2为位置反馈的跟踪信号和其微分，被扩张状态量z3可以对控制系统的未知扰动做出估计；e为观测的误差；非线性幂次函数fal(e,α,δ)的表达式如下。

2.1.3 非线性状态误差反馈设计

充分利用其非线性函数的特性，实现“小误差大增益、大误差小增益”[12]的控制效果。具体表达式如下。

2.2 变论域双模糊自抗扰控制

自抗扰控制(ADRC)方法不依赖控制对象精确的数学模型，对系统内外的不确定性干扰，能够进行有效的预估并补偿。但是，传统ADRC中需要调整的参数众多，整定过程复杂[13]，为了方便工程应用和简化参数整定过程，结合自适应模糊控制理论，本文提出一种变论域双模糊算法对自抗扰参数进行在线自整定。利用模糊控制具有模拟人脑逻辑思考的能力[14]，引入伸缩因子的概念，以二级模糊控制调节一级模糊控制的比例（输出）因子，改变其输出论域，使得最终输出变量能够随着误差的变化在一定范围内自动调节，提高控制系统的自适应性和鲁棒性，改善控制效果。

2.2.1 二级模糊控制

取观察误差e1=y1−z1和e2=y2−z2为模糊控制的输入量，其中e2为e1的 微分。输出为 ∆β1、∆β2，分别表示自抗扰控制中的可调参数 β1、β2的变化量，即应用模糊规则，将非线性状态反馈中的控制参数修正为

其中：β1、β2为控制器的初始参数值。

为了方便编程，选用三角形函数作为隶属度函数，采用Mamdani型为模糊推理理论，并基于重心法Centroid解模糊化。每个输入输出语言变量取5个语言值：负大(NB)、负小(NS)、零(0)、正小(PS)、正大(PB)。按照实际情况，将输入变量的论域取为[−1,1]，将输出变量的论域取为[−3,3]。将模糊推理模块的输入和输出参数分别模糊化，其对应的隶属度函数图像如图4所示。

图4 输入输出变量的隶属度函数图像

基于减小误差的原则，制定针对模糊自抗扰中NLSEF 2个参数 ∆β1、∆β2的模糊规则，如表1所示。

表1 ∆β1、∆β2模糊规则表

2.2.2 一级模糊控制

为了实现二级模糊控制比例因子的调节，引入伸缩因子 γ的概念。根据输入变量e和ec来推理输出论域伸缩因子，并将 ∆β1、∆β2的输出论域分别乘以γ1和 γ2。输出论域伸缩因子 γ1、γ2的模糊规则表如表2所示。输入变量与一级模糊控制器相同，输入变量的模糊论域都为[−4,4]，语言值用{NB,NM,NS,ZE,PS,PM,PB}表示。输出变量为伸缩因子γ1、γ2语言值用{很小，小，中，大，很大}表示，对应模糊集合{VS,S,M,B,VB}，输出变量的论域为[0,l]。

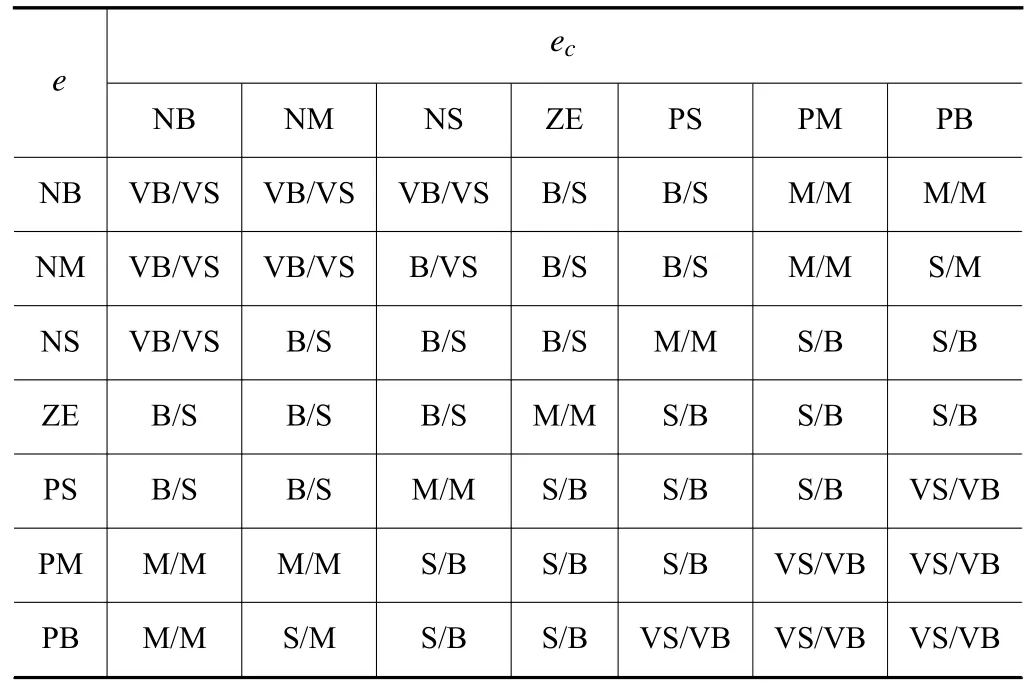
表2 γ1、γ2模糊规则表

非线性状态反馈中的控制参数最终修正如下。

3 结果与分析

3.1 实验平台

为了验证所提算法的有效性，对变论域双模糊自抗扰控制系统进行试验分析，实验平台如图5所示。该实验平台通过实时数字控制系统RTU-BOX实现控制算法，采用主频为300 MHz的32 位浮点型数字信号处理器TMS320C28346作为数字控制器；驱动器可以将控制器的PWM信号放大以驱动直线执行器，直流电源给驱动器供电。位置传感器用来提供位置反馈并将数据传递给上位机。电磁直线执行器的参数如表3所示。

图5 实验平台

表3 电磁直线执行器参数值

3.2 算法验证实验

为验证算法的有效性和电磁直线执行器在实际运行过程中的响应和跟踪性能，进行了阶跃目标位移响应工况、正弦信号跟踪工况的实验，实验与仿真对比结果如图6所示。

图6 阶跃目标响应实验曲线

图6为给定10 mm阶跃位移信号下变论域双模糊自抗扰控制实验与仿真对比曲线。从图中可以看出，实验与仿真曲线皆能迅速到达稳态，稳态精度良好，仿真曲线稳态精度趋近于零，实验曲线稳态误差也保持在0.025 mm以内，实验结果与仿真结果相差很小。这不仅说明了本文所提出的变论域双模糊自抗扰控制方法具有良好的控制精度，也验证了所提出的控制算法的有效性。

图7为给定电磁直线执行器指定正弦波信号0.005sin(20 πt)+0.005实验与仿真对比曲线。从图中可以看出在5 mm左右能够跟踪上正弦曲线啊，在10 mm左右达到稳态，稳态误差在0.3 mm左右。在对比曲线第二个峰值处，仿真和实验曲线相位滞后时间分别为0.95 ms和1.17 ms；相对误差分别为0.039%和1.1%。实验结果和仿真结果相差很小，误差保持在2%以内。

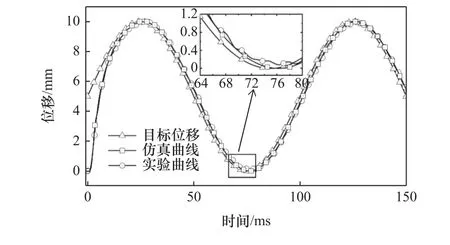
图7 正弦轨迹跟踪实验曲线

实验过程中由于直流电源电压的限制、内部非线性干扰以及位置传感器测量精度的限制，实验结果的响应时间以及稳态精度比仿真结果有一定的差距，但均能很好地跟踪给定工况下的目标位移且误差均保持在2%范围以内，表明了实验结果与仿真结果的一致性，验证了所提出的控制算法的有效性。

3.3 鲁棒性分析

由于电磁直线执行器取消了中间环节，导致系统内外部的非线性因素和不确定性干扰会直接作用于执行器上，因此要求执行器控制系统具有较强的抗干扰能力和一定的自适应鲁棒性。为了验证变论域双模糊自抗扰控制器对外部突变扰动的抑制能力，在35 ms时使得负载从0 N突变为60 N，图8为两种控制方法系统响应曲线的对比图。由于突变负载的影响，一直稳定在目标位移附近的电磁直线执行器在35 mm时迅速偏离目标位移，并在控制器的作用下迅速回到目标位移，但由于系统惯性太大，位移曲线产生了两个振荡周期，之后执行器再次回到目标位移并一直保持稳定。由图8中可以看出变论域双模糊自抗扰控制在位移偏移量和调节时间上均明显小于普通自抗扰控制，位移偏移量为普通自抗扰控制的58%；并且其稳态误差趋近于零，稳态精度较高。结果表明，所设计的双模糊变论域自抗扰控制器在具有良好的阶跃位移响应性能和控制精度的同时，还具有较好的抗干扰能力和自适应鲁棒性。

图8 35 mm附加突变负载响应曲线

随着电磁直线执行器通电时间的增加，电磁线圈的温度会升高，从而导致线圈电阻发生变化，电阻变化是对执行器系统影响最大的系统参数变化。为了验证本文所提出的控制方法对于系统参数扰动的抑制能力，增加执行器电阻，使得执行器电阻由初始值1.17 Ω增加到2.5 Ω。

图9为执行器电阻发生变化时，两种控制方法的对比响应曲线。由图中我们可以看出，当系统内部参数发生变化时，变论域双模糊自抗扰控制在响应阶段的超调量与稳定时间明显小于自抗扰控制；其稳态时的误差趋近于零，小于自抗扰控制的误差，具有良好的控制精度。结果表明变论域双模糊自抗扰控制具有良好的参数扰动抑制能力和较好的鲁棒性。

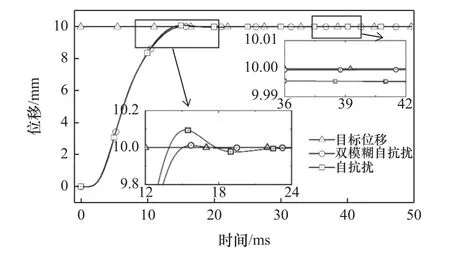
图9 电阻变化时系统响应曲线

为验证控制器对外部白噪声干扰下的控制性能，对正弦信号yt=0.01sin(50t)施加一定功率的随机白噪声干扰，跟踪性能及误差如图10所示。由图可知在附加白噪声干扰下，两种控制方式都存在一定程度的振荡，但变论域双模糊自抗扰控制的跟踪误差与稳定性都优于普通的自抗扰控制，具有优秀的连续位移目标跟踪性能。这说明系统在运动过程中受到持续的外界信号干扰时，变论域双模糊自抗扰控制能够克服外部扰动带来的不利影响，拥有更好的鲁棒性和跟踪性能。

图10 外加白噪声干扰下轨迹跟踪对比曲线

4 结语

本文针对具有内部参数扰动和外部不确定性干扰的电磁直线执行器系统，提出了一种电流环采用PI控制，位置环采用变论域双模糊自抗扰控制的双闭环控制方法。其在阶跃工况下不仅具有较高的稳态精度，在施加突变负载扰动和内部参数扰动的情况下还具有良好的自适应鲁棒性；在施加白噪声的正弦工况下，依然具有较强轨迹跟踪性能。