基于混合核函数高斯过程的大坝变形预测方法

李维华，娄健康，李 星

（1.黄河勘测规划设计研究院有限公司，河南 郑州 450003； 2.水利部黄河流域水治理与水安全重点实验室（筹），河南 郑州 450003； 3.河南省豫北水利勘测设计院有限公司，河南 郑州 450046； 4.南京水利科学研究院，江苏 南京 210029）

1 引 言

为充分开发利用水能资源，我国在西南地区修建了一大批200～300 m 特高拱坝，这些高拱坝普遍位于地质条件恶劣的深山峡谷地区。其运行过程中会承受如极端温度荷载、超限制水位洪水荷载、地震荷载等多种不利荷载的叠加作用。保障高拱坝全生命周期安全稳定运行是当前大坝安全管理工作的重点。

大坝结构安全监控通过在大坝坝体内部及地基布置大量传感器，实时感知和评估多种结构相关的物理量，如变形、渗流、应力、裂缝开度等［1］。准确有效预测大坝在多重环境荷载组合作用下的结构响应及行为变化，对于大坝运行维护、安全预警具有重要意义。变形是混凝土坝在多种荷载叠加作用下的真实反映，是安全监控的重点内容。大坝变形预测模型依据方法手段的不同，可分为统计模型和人工智能模型。传统统计模型主要是将大坝变形分解为水压分量、温度分量和时效分量三部分，通过多重线性回归、逐步线性回归等统计学方法，依据输入环境变量预测大坝变形［2］。传统统计模型只能考虑输入和输出变量间的线性关系，而大坝变形是结构性态在环境因子作用下的非线性响应，使得统计模型预测能力受限，很难准确、高效、长期预测变形。

人工智能算法主要是通过人工神经网络、支持向量机等机器学习算法，充分挖掘大坝监测数据里的信息，实现大坝环境变量和输出变量的非线性关系精确模拟［3］。许多学者在人工智能算法预测大坝变形方面开展了研究，如：李明军等［4］提出一种基于改进灰狼优化算法和支持向量机的大坝变形组合预测模型；陈优良等［5］提出一种基于极限学习机和弹性网络支持的大坝位移预测方法，试验结果表明该方法可简化隐含层神经元个数选择问题，便于参数调整；杨恒等［6］将支持向量机（SVM）和差分自回归移动平均模型（ARIMA）结合，提出一种时间序列大坝位移预测分析方法，可实现大坝位移变化趋势的精确预测，具有一定实用价值。然而这些方法普遍存在易陷入局部最优、过拟合、调参过程复杂等缺陷，限制了其应用。此外，这些方法并未考虑大坝变形受多环境因素交叉耦合的影响，因此有必要研究考虑多环境因素交叉耦合影响的大坝变形预测方法。

高斯过程回归是一种基于贝叶斯理论的机器学习方法，它可为概率回归预测提供一个灵活简捷的建模框架。已有许多学者应用高斯过程回归解决实际工程问题［7－8］，高斯过程回归在解决高维度小样本问题时优势显著，可有效评估监测信号的不确定性行为，精度高、泛化能力强。

协方差函数是高斯过程回归的重要组成部分，也是高斯过程回归实现非线性预测的基础。然而常规线性协方差函数只能处理平稳序列，大坝变形时间序列是一种非平稳时间序列，因此有必要研究组合协方差函数以更好地考虑大坝变形时间序列的非平稳性。

2 基于改进高斯过程回归的大坝变形预测方法

2.1 基本原理

高斯过程回归是一类随机变量的集合，任意有限个随机变量具有一致的联合高斯分布，典型高斯过程f（x）（x为影响大坝位移的环境因子，如水位、温度、时效等）可以用其均值m（x）和协方差函数C（x，x′）（x为训练集的模型输入，即训练集对应的环境因子；x′为测试集的模型输入，即测试集对应的环境因子）来近似描述［9］，为了便于简化，均值函数通常设置为0。

式中：ε为独立同分布的白噪声，即ε～N（0，），σn为噪声标准差，任何有限数目观测值均可形成高斯过程［9］。

高斯过程的后验分布可以通过对给定数据训练集和测试集进行联合先验分布来推导：

式中：f∗为用于验证的新输入数据；X为输入监测变量；为输出结果的平均值；v（f∗）为验证集上模型的输出结果。

此外，高斯过程不仅能给出预测值，还能利用协方差函数估计输出预测值的置信度。作为一种非参数估计方法，高斯回归的预测值只取决于输入变量和观测值，而模型超参数Θ可视为高斯过程回归的超参数。最大似然估计是高斯过程回归的常用参数估计方法，最大似然函数通常可由贝叶斯理论获得：

参数估计通过最大似然估计获取。

2.2 核函数

协方差函数控制模型估计未知函数时数据平滑程度，其选取对模型非线性重建性能影响显著。最常见的协方差函数是平方指数协方差函数，其主要应用于平稳序列建模，而大坝位移时间序列是一个典型受多因素影响的非平稳时间序列。本研究为进一步提高高斯过程回归模型对非线性时间序列的建模能力，引入组合协方差函数概念，通过组合Matern 核函数和白噪声核函数，构造如式（4）所示的非平稳协方差函数，以更好地体现输入和输出变量间的非线性关系。其中，白噪声核函数主要用于解释信号的噪声是独立和正态分布的，式（4）中参数noise＿level等于该白噪声的方差。

式中：k（xi，xj）为协方差函数；xi、xj为第i个和第j个样本数据；d（xi，xj）为欧氏距离；Kν（·）为修正贝叶斯函数；ν为数据序列的均值；l为修正线性激活函数值。

2.3 模型性能评估指标

为量化评估上述方法和现阶段常用的多重线性回归（HST）、随机森林（RF）和支持向量机（SVR）的预测精度和泛化能力，本文选择确定系数R2、均方误差MSE和平均绝对误差MAE作为大坝变形预测的评价指标。

3 工程案例研究

3.1 工程概况

某混凝土高拱坝，位于黄河上游，坝型为混凝土双曲拱坝，最大坝高为105 m，水库正常蓄水位为700 m、死水位为660 m。大坝布置5 组正、倒垂线监测点，其中：PL 为正垂线，用于监测大坝坝体位移；IP 为倒垂线，用于监测大坝坝体相对地基的位移。

3.2 监测数据

本研究选用2014 年1 月1 日至2017 年12 月31日大坝正、倒垂线1 451 个监测样本数据用于模型建立和验证，其中2014 年1 月1 日至2016 年12 月31日共计1 086个监测样本数据用于模型训练和验证，2017 年1 月1 日至2017 年12 月31 日共计365 个监测样本数据用于模型测试和泛化能力评估。图1 为2014—2017 年水库水位变化曲线，可以看出库水位基本呈现以年为周期的规律性变化，平均年变幅为10.425 m 左右。选用3 个典型正垂线监测点PL13－1、PL15－1 和PL16－1 用于评估模型的有效性。3 个典型监测点的位移过程线如图2 所示。

图1 2014—2017 年水库水位变化曲线

图2 3 个典型监测点位移过程线

3.3 结果比较与分析

利用3 种常用的大坝变形预测分析方法即多重线性回归、随机森林和支持向量机方法作对比来验证本文方法的泛化能力，3 个典型大坝位移监测点位移预测值与实测值对比见图3～图5。

图3 PL16－1 监测点位移预测值和实测值对比

图4 PL13－1 监测点位移预测值和实测值对比

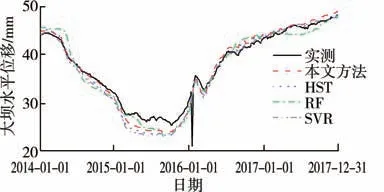
图5 PL15－1 监测点位移预测值和实测值对比

可以看出，本文所提的基于组合核函数的高斯过程回归的预测值与实测值趋势基本保持一致，而多重线性回归方法存在一定程度的偏差。这主要是由于高斯过程回归对非线性关系的拟合能力更强，因此在长序列大坝变形分析上更具优势。3 种量化评估指标下本文方法和对比方法在测试集上的回归性能评估结果见表1，可以看出，高斯过程回归大坝变形预测方法性能优于对比方法，这验证了其泛化能力。

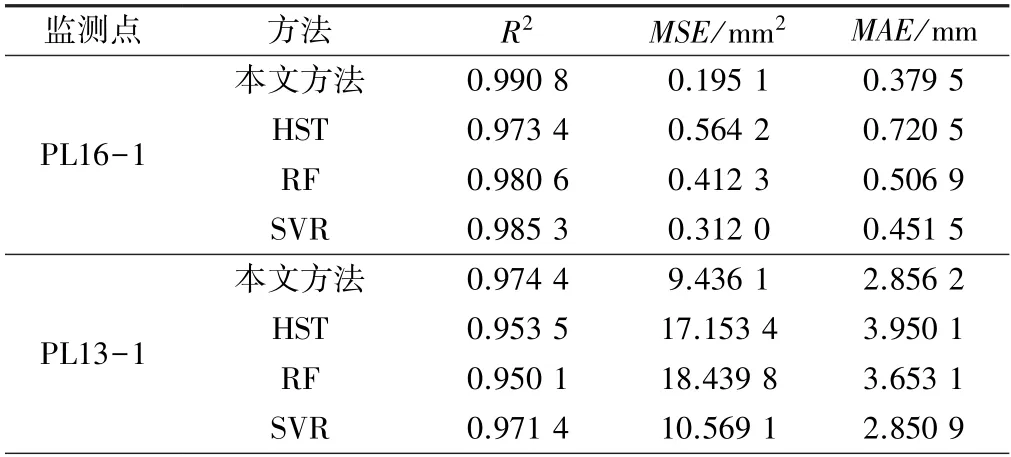
表1 不同方法测试集性能评估结果

续表1

图6 为本文方法和对比方法的回归结果残差对比图，可以看出，本文方法的残差分布更集中，更接近于0，且其超过1.5 倍阈值区间实测值数目显著少于对比方法的，这说明本文模型的鲁棒性更好。

图6 本文方法和多重线性回归（HST）、随机森林（RF）、支持向量机（SVR）方法残差对比

4 结 论

本文提出基于混合协方差函数高斯过程回归的大坝变形非线性预测分析方法，可简捷地建立大坝结构行为预测模型，并给出结果的概率非参数估计。计算结果表明，该方法在大坝典型监测点位移分析中效果较好，确定系数、均方误差等评估指标均显著优于现有主流大坝变形预测方法，说明了该方法预测大坝变形具有优势。此外，该方法可进一步用于识别潜在大坝监测数据异常信息，可为大坝结构性态评估与风险鉴定提供参考。