海绵型道路横断面排水设计参数优化
2023-03-10咼贵春肖传语
咼贵春,肖传语,孙 悦
(1.华设设计集团股份有限公司,江苏 南京 210000;2.东南大学,江苏 南京 210096)
0 引 言
“海绵城市”道路多选择大孔隙沥青材料路面。大孔隙路面排水能力强,在雨天路表不产生大量积水,确保车辆与道路之间能充分摩擦,路面的抗滑水平明显提升,避免交通意外的出现,保证了交通安全[1]。
国内外针对交通安全的研究明确指出,路表水膜是交通安全的隐患之一[2]。针对水膜厚度与滑水现象的相关性,研究人员通过实验以及建立模型,得到给定水膜厚度下的抗滑-速度关系[3],通过模拟路表水膜,研究了路表积水情况[4]以及水膜厚度与构造深度等路面参数的相关性,并根据接触面材料的弹性变形及润滑剂流变特性给出了滑水的边界方程[5]。在降雨强度超过设计值时,车轮荷载将路面积水从孔隙中排出,使车轮与路面能够充分摩擦,保证了排水路面的抗滑性能[6]。
路面的排水渗流条件决定了其抗滑能力。Umiliaco等人[7]根据随机序列吸附与格子玻尔兹曼方法设计了非恒定流路面模型,并研究了大孔隙路面渗流特性。Chandrappa[8]使用科泽尼-卡尔曼方程得出孔隙率与渗透特性的相关性,观察到非线性的达西定律,研究了孔隙参数与渗透能力的关系。虽然大多数研究得到了路面渗透率的基本模型及影响因素,但对线性上存在差异的排水渗流情况还缺少研究。
对于路面内部排水特性的研究,Mahboub[9]采用有限元软件对路面结构进行稳态渗流分析。结果表明雨水渗入路面内部是面层与基层较大的渗透系数造成的。刘明[10]取道路横断面进行非饱和渗流模拟,结果显示当降雨量相同时,延续时间长的降雨将渗入更多。
海绵型道路的抗滑性能比普通道路更高,也能够更好地保证交通安全[11]。利用海绵型道路需要进行海绵型道路的横断面优化设计。海绵型道路横断面优化设计参数主要有横坡、断面宽度、车道数等。现有研究更多地限于排水路面的结构与材料设计以及功能性路面等方面,针对海绵道路的横断面优化设计研究较少,主要依旧选择常规道路几何参数。
基于海绵型道路路表渗流与产流的规律,建立了二维与三维路面渗流模型研究海绵道路排水能力。依据海绵型道路的排水优势,对道路关键横断面和纵断面设计参数开展定量研究,提出优化建议。
1 OGFC面层基础模型
OGFC沥青混合料多应用于海绵城市的道路建设中。其抗磨耗、抗滑、排水性能较好,有较大的孔隙率,一般约为20%[12]。
本文构建了OGFC面层模型,模型简化图如图1所示。该模型断面为一梯形,其中路面宽平行x轴,厚平行y轴,由于断面右低而左高,水在路面中从左往右运动。潜水高度为H,h则代表它的深度。O点与某一断面相距x,该处的潜水高度为潜水厚度与排水面层层底的相对高度之和。此外,-dH/dx代表水力梯度,h是过水断面。
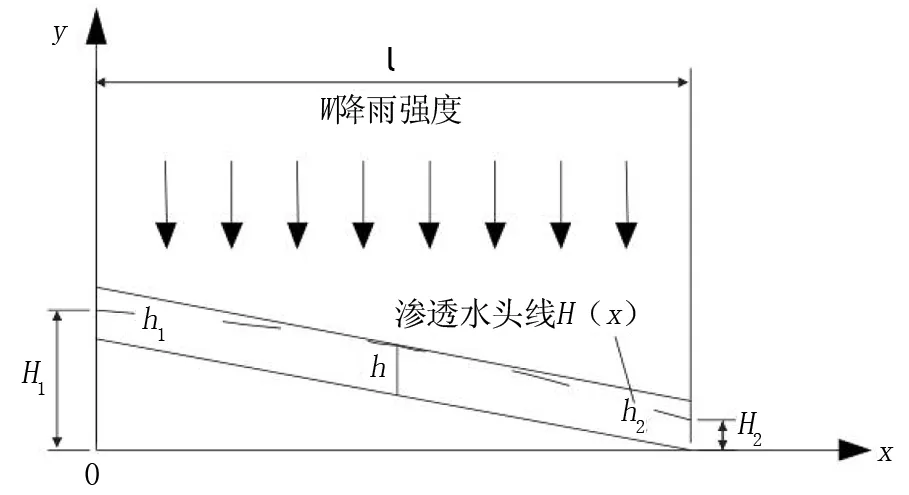
图1 路面几何模型简化渗流图
根据Boussinesq方程,写出如下方程
(1)
H|x=0=H1
(2)
H|x=1=H2
(3)
式中:H1、H2为两侧潜水水位的高度,cm;w为入渗强度,cm/s;k为排水面层的横向水力传导系数,cm/s。
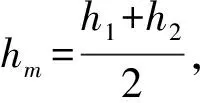
(4)
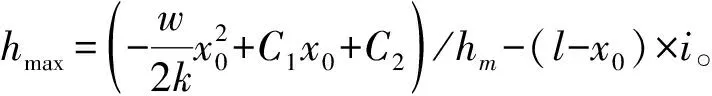
选择饱和、不饱和材料来分析OGFC模型中非饱和渗流情况。OGFC材料的渗透系数函数与水土特征曲线拟合参数的可取值范围较广,根据实验结果和Seep/w中的数据库参数,单位体积含水量由简单方程法得到[14]。本研究构建数据点函数模型分析集料直径。根据孔隙比,得出该OGFC混合料饱和含水率为18%。由级配曲线易知直径大于0.6 mm的有10%,大于8 mm的有60%,求出吸力最大值为20 kPa。由Seep/w生成水土特性曲线,如图2所示。
为计算水压传导系数应用了Van Genuchter模型,采用Seep/w结合水土特征曲线得到水力渗透系数曲线如图3所示。
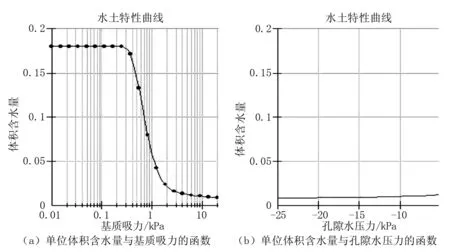
图2 材料水土特性曲线
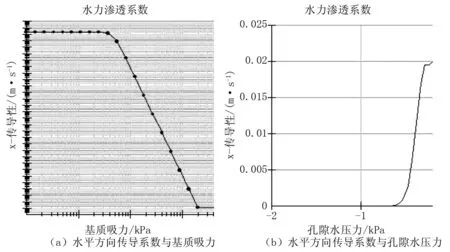
图3 材料水力渗透系数曲线
由于排水沥青路面为隔水透水层下卧封层,设模型下部与初始水头位置相同,使用单位流量来满足降雨条件,并在顶面对单位流量作出限制。OGFC模型右下方设置出水口,该处压力水头取0。假设其余边界不与外界进行流量交换。中国气象局使用150 mm/h划分强大暴雨与中大暴雨,取其为设计降雨强度。
2 横断面设计优化
为使路表排水畅通,直线段的路面上一般有2%的路拱横坡,为追求经济效益最大化,保证行车安全只需使路表不产生径流,因此考虑放宽路拱横坡的设置指标。在路面内部排水顺畅的前提下,研究分析了减少路拱横坡度的范围。由于直线段路面沿路中线对称设计,只进行断面一侧的建模既能保证计算的准确性又能减小计算量。为研究不同等级道路,路面模型选取双向二至八车道的一侧,其中车道宽3.75 m。考虑到路缘带与硬路肩的宽度,最终路面宽度在车道宽度之和的基础上加0.75 m。
在我国各级公路沥青上面层的层厚通常设为4 cm,若常规的2%路拱横坡的排水层无法满足排水要求,则不选择提高路拱横坡值,而是增厚排水层。需要注意的是,考虑到多余流量在设计预期无法满足最大降雨量时可沿路表流出,本研究不分析路拱横坡为0的模型。
2.1 仅考虑横坡的二维渗流路面模型
(1)双向两车道半幅模型
双向两车道模型总宽度为4.5 m,经模拟分析,模型在60 s后达到平衡状态。如图4所示,在模型中,曲线向上凸出,压力水头极值未高于40 mm,且左侧的压力水头小于0。可知双向二车道路面横坡等于2%时排水畅通。
为获得更高经济效益将横坡降至0.5%。如图5所示。横坡0.5%面层排水模型在达到平衡状态后压力水头大于0,与横坡2%的情况相同的是曲线未超过40 mm可知横坡为0.5%时排水畅通。
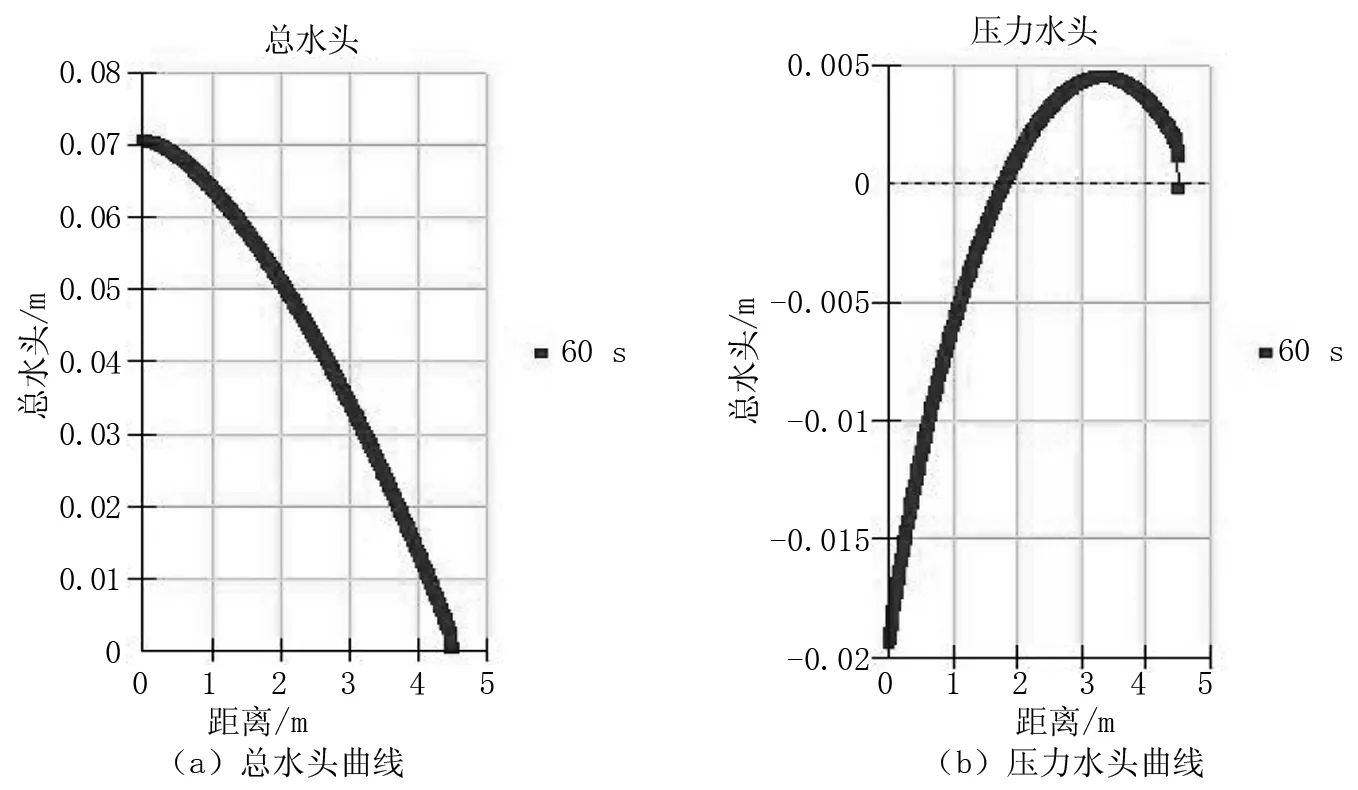
图4 双向二车道半幅模型(横坡2%)压力水头及总水头曲线
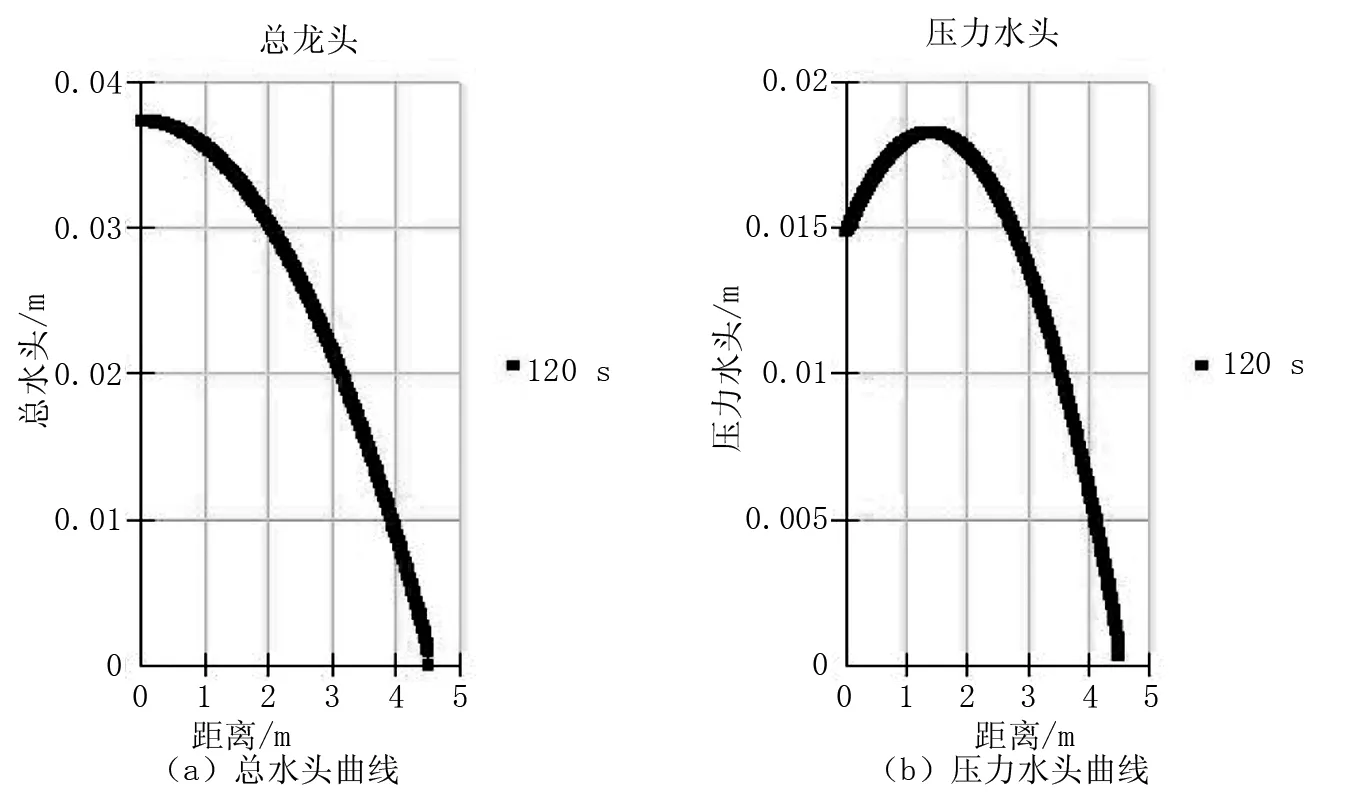
图5 双向二车道半幅模型(横坡0.5%)压力水头及总水头曲线
(2)双向四车道半幅模型
双向四车道按同样方法进行模拟。路拱横坡取值为1%,排水层厚40 mm,模型达到平衡状态时压头最高处超过40 mm。将路拱横坡增至1.5%,压头最高处未超过层厚,满足排水路面功能需求。
(3)双向六车道半幅模型
双向六车道路拱横坡取值为2%,排水层厚40 mm,模型达到平衡状态时压头最高处已超过40 mm。将排水层厚度增加为50 mm,压头最高处未超过排水层厚度,满足排水功能需求。
(4)双向八车道半幅模型
对于双向八车道路面,分析后发现在路拱横坡为2%以内时,无论路面厚度取4 cm或5 cm都不能达到排水畅通的需要。
考虑把排水层设计为双层排水结构,将其增厚至10 cm[15],横坡设为0.5%,模型达到平衡状态时压头最高处不超过排水层厚度,满足排水功能要求。
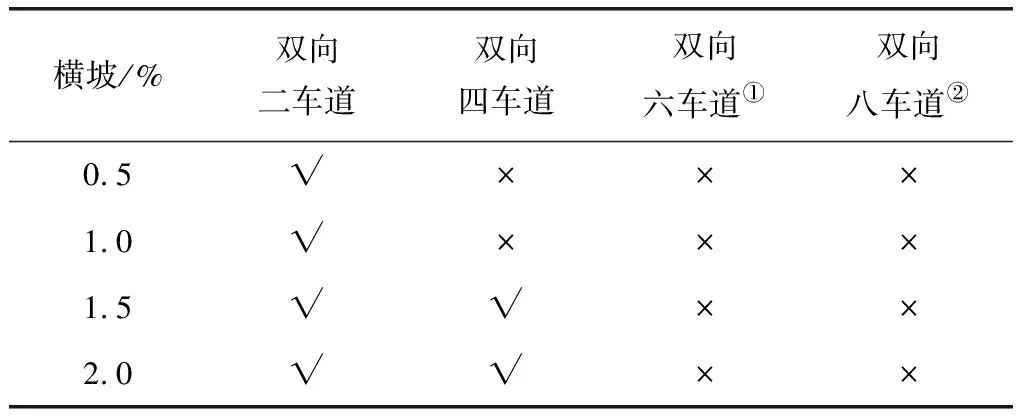
表1 仅考虑横坡的4 cm厚路面 渗流模型可用横坡情况
将四种仅考虑横坡的二维路面模型的所有计算结果列于下表,其中“√”表示排水畅通,“×”表示路面不满足排水要求。横坡取2%时,双向六与八车道压头最大值大于排水层厚,不符合排水要求,在这种情况下增加排水面层厚度以及将路面设计为双层排水结构是可取的。
2.2 考虑合成坡度的三维渗流模型
在考虑纵坡的情况下建立路面三维渗流模型。三维模型中的降雨量、渗流系数以及路面几何尺寸根据上文的二维模型的取相同值。整个模型长40 m,纵坡初始值取0.5%。
基于二维渗流模型的条件,在三维渗流模拟过程中设以下3个限制:(1)由于雨水会渗入到面层中,为模拟路面降雨可在模型上侧给定流量值;(2)将边沟附近的一面作为唯一渗流面,且雨水仅能通过出水口排出;(3)除了上侧和边缘渗流面,模型不与外界进行交换。
对该路面模型进行计算分析,压力水头云图如图6所示,可观察到压力水头未超过40 mm,与相同横坡的二维模型相比,三维模型的压力水头较大。

图6 压力水头云图
在对不同车道数的路面模型在特定条件下的渗流情况模拟后,结果在下表列出,其中“√”表示排水畅通,“×”表示路面不满足排水要求。
由表2可知,不同横坡下渗流能力差异较大,路面的排水能力与横坡坡度呈正相关;若横坡一样,纵坡的增加会延长排水路线,导致排水能力变差;当合成坡度一样时,更大的横坡能让排水较为顺利;在各种条件中,双向两车道的排水性能最优,在横坡为2.0%的条件下,路面排水在任何纵坡下都能符合要求;过宽的路面会极大影响排水性能,双向八车道的的路面,需要横坡2.0%,纵坡0.5%时才能满足排水要求。
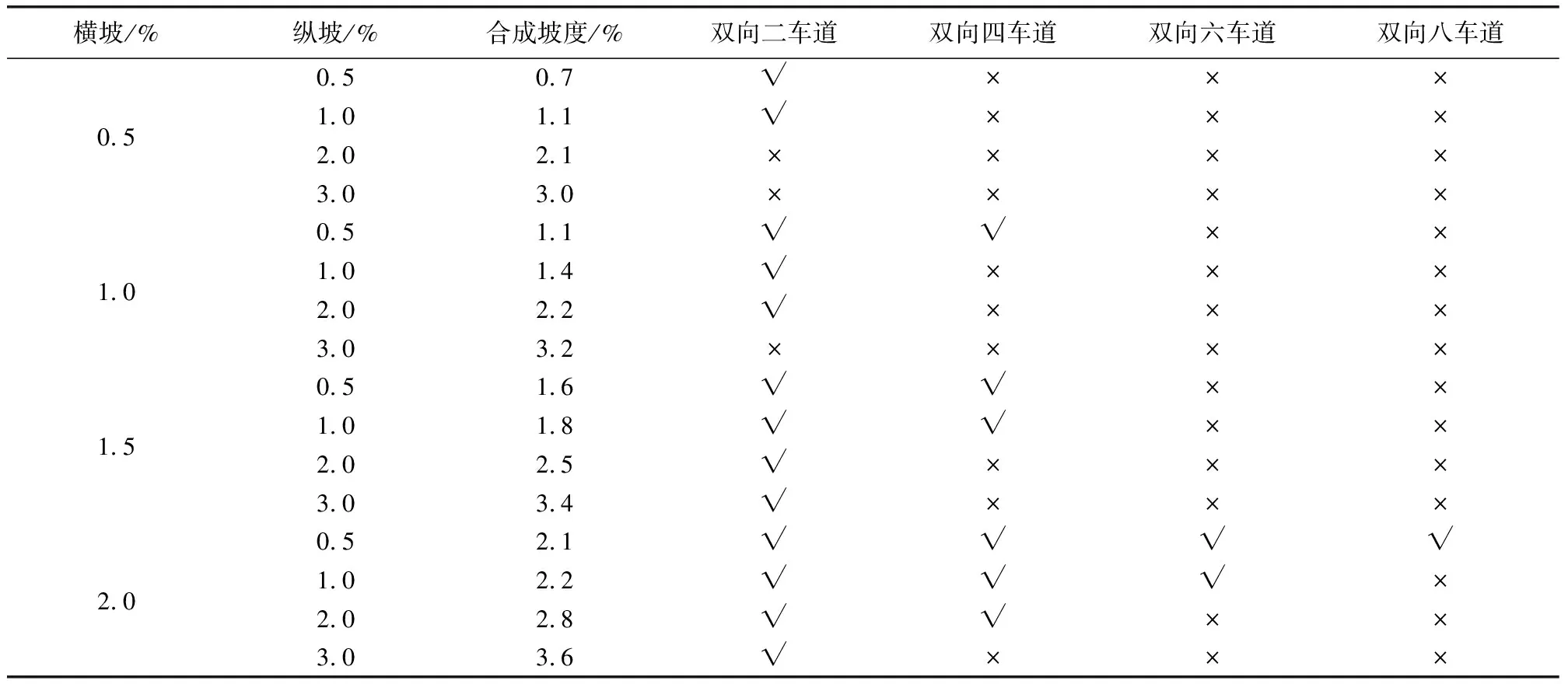
表2 三维渗流模型路表水膜产生情况
3 总 结
基于道路横断面的各类参数,建立了路面在饱和与不饱和状态的渗流模型,通过对路面的渗流与时间的关系进行分析,建议横断面各项参数进行下列改进。
二维渗流模拟仅考虑横坡,对于双向二车道路面,横坡不大于2.0%时均能满足排水要求;对于双向六车道路面,常规的横坡均无法达到4 cm厚的排水层的排水要求,若将排水层增厚至5 cm则能满足要求;对于双向八车道,需设计双层排水结构,将排水面层增厚至10 cm。
三维渗流模型考虑纵坡,模拟后发现在各种组合中,双向二车道路面的表现出最好的排水性能,当横坡取2.0%时,路面在任意纵坡下都能满足排水要求;双向八车道的模型,纵坡为0.5%时,将横坡提高至2.0%才能满足排水要求。
海绵型道路的各参数的优化建议值见表3。

表3 海绵型道路的几何设计指标优化建议
