集输管道多相流冲刷腐蚀数值模拟研究

姚景，郝成名，王树立，李祉睿，徐慧

(1.泉州职业技术大学能源学院，福建 晋江 362268；2.福建省清洁能源协同创新中心，福建 晋江 362268)

0 引言

油田在开发中后期，为了保持原油储层中压力并提高原油的采出率，需向油层注水开采。由于管道所经地域的地形以及地貌的差异，当油水流经集输管道时极易形成油水乳状液[1-4]。在长期的油品输送过程中管道中会存在小颗粒的砂粒以及其他杂质在弯头处沉积，这给管道运输油品带来很大的安全隐患，且油水两相中水分的存在会导致管道发生空化腐蚀。江山等[5]对90°大曲率圆形截面弯管内部流体三维数值模拟在fluent软件中，RNG k-å湍流模型在弯管内部流态可以准确地反映。林楠等[6]分析了冲蚀磨损与固体颗粒的运动的轨迹之间的关系，提出弯头处流体的颗粒杂质的入射角度对于管道的腐蚀速率有影响，同时发现管道的的曲率半径和外形都可以减小管道弯头处的冲蚀速率。管道流体流体力学因数对管道的冲蚀速率影响很大。彭文山等[7]研究了管道的弯径比、管道直径、弯曲角度对含砂两相流管道的冲刷腐蚀规律，考虑颗粒碰撞模型的冲蚀作用情况，发现弯管冲蚀严重区域有弯头侧壁、弯头连接处、下游直管段的外侧，随着管道物性的改变，冲蚀严重区域也会发生随着发生变化。李亮[8]等研究了注汽管网中气、液、固三相对弯管形成的连续冲刷，造成弯管的腐蚀泄漏现象。研究发现在弯管弯曲程度的增加时，液相和颗粒相分布、壁面磨损区域均会逐步向弯管的出口直管段移动，且在该段的冲刷腐蚀速率逐渐增大；增大管壁处油相体积分数可有效降低固相颗粒对管道壁面的冲刷腐蚀。冉亚楠[9]等研究了弯曲半径对不同结构弯管液固两相流冲蚀磨损影响，且发现在弯曲半径较大时，冲蚀损伤部位集中在弯头外壁面和出口直管段外壁面。通过对管径的研究发现：最大冲蚀速率随管径增大而减小。

高黏度油品在长距离输送管道中流动时，由于地质条件的变化，在一些特殊地段，需要采用特殊管段输送油品，但是国内外对于管道腐蚀产生的影响因素研究较少，文章通过对比管道中不同的入口速度、不同粒径、不同含水率对于管道腐蚀速率影响进行了研究分析。

1 建立模型

1.1 几何模型与网格

文章以集输管道中120°弯管进行数值模拟，整个管道分为三段，L1、L2、L3三段，弯管管径为D=250 mm；弯径比3，其几何模型如图1所示，网格示意图如图2所示。

1.2 计算模型的建立

1.2.1 连续相控制方程

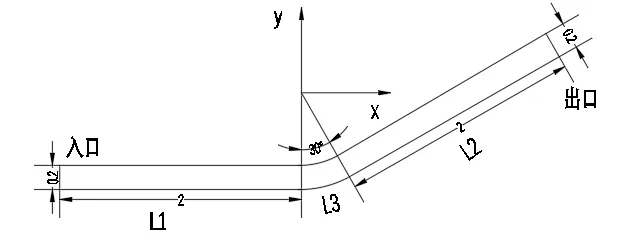
图1 弯管二维结构示意图

图2 弯管网格图

式中：ai为第i相体积分数；ρi为第i相的密度(kg/m3)；为第相的平均速度(m/s)[10]。

1.2.2 动量方程

式中：P为压力(Pa)；τk分子动力(N/m2)；τk为紊动应力(N/m2)；Mk单位体积相间动量传递(N/m3)；(Fint)k内在力(N/m3)；g为重力加速度(m/s2)；SD为动量源项(N/m3)[10]。

1.2.3 湍流方程

其中：

式中：ε为湍流耗散率(W/m3)；k为湍流动能(J)；μt湍流黏度(Pa·s)；k湍流动能(J)；YM可压湍流中脉动扩张的贡献；Gk是平均速度引起湍流动能产生项；Gb浮力引起的湍动能k产生项；Sk，Sε自定义无因次参数。C1ε=1.44，C2ε=1.92，Cμ=0.09为经验常数。

1.2.4 离散相控制方程

DPM模型积分Lagrangian坐标系下离散颗粒的运动方程计算运动轨迹。固体颗粒在两相流中受到马格努斯(Magnus)力、绕流阻力、萨夫曼(Saffect曼)力、重力、Basset力、附加质量力、压力梯度力等作用力，受受力平衡与颗粒的惯性作用，分散相的颗粒运动方程如下[11]：

式中：ua砂粒速度(m/s)；ρa砂粒密度(kg/m3)；u连续相速度(m/s)；da砂粒直径(μm)；gyy方向重力加速度(9.8 m/s2)；Rea相对雷诺数；CD曳力系数；Fy为y方向的其他作用力。

1.2.5 冲蚀理论模型

在Fluent数值模拟软件中颗粒腐蚀与沉积模型适用于文章的研究[12]。

式中：Re为壁面腐蚀速率(kg/(m2·s))；N为碰撞颗粒数目；ma为颗粒质量流量(kg/s)；C(da)为颗粒直径函数；θ为颗粒对壁面侵入角(°)；f(θ)为侵入角函数；d(u)为相对速度函数，取2.6 m/s。

1.3 边界条件以及数值算法

管道中流体为油水固流体三相，在常温下进行输送油品，其中原油黏度2 895 Pa·s，原油密度为865 kg/m3，管道中固体的颗粒密度2 550 kg/m3，入口颗粒质量流量为2.5 kg/s，弯管中含水率在40%～60%之间变化。入口采用VELOCITY-INLET(速度入口)壁面粗糙为10 μm，粗糙常数为0.5；出口采用PRESSUREOUTLTET(压力出口)。

2 弯管的模拟分析

2.1 不同入口速度

管道中的颗粒粒径为200 μm，入口速度为0.4 m/s，含水率在30%～50%之间变化。数值模拟研究发现40%、50%、60%含水率时管道内外管道壁冲刷腐蚀速率(图3)。

图3 管道冲蚀图

如图3所示含水率与管道冲刷腐蚀的关系成正比，且随着含水率增大而增大，管道的腐蚀发生在管道的弯头处以及管道弯头与直管的连接处，这是由于裹挟在管道乳状液中的颗粒数目减小，而沉降率增大而导致管道的腐蚀速率增大。

由模拟结果可知，在含水率不同的条件下，管道管道壁面的冲刷腐蚀速率与入口速度的关系如图4所示。

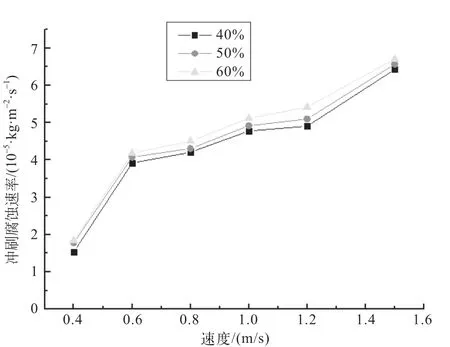
图4 入口速度与冲蚀速率关系曲线图

由图4可知，入口速度0.4 m/s～0.6 m/s，管道的冲刷腐蚀速率急剧增加；入口速率大于1.2 m/s时，冲刷腐蚀发生急剧变化，当入口速率为0.6 m/s～1.2m/s时，冲刷腐蚀速率是在平稳变化。因此，从冲蚀速率的角度来看，在集输管道中输送高粘油的油品时流速应控制在0.6 m/s～1.2 m/s为最佳。

2.2 不同的含水率

管道中的颗粒粒径为200 μm，含水率在50%，多相流入口速度在0.8 m/s～1.5 m/s之间变化时，管道的外壁面冲刷腐蚀速率如图5所示。

如上图4所示当油水乳状液入口速度增大情况下，管道外壁冲蚀速率也增大。在管道中腐蚀严重的部位向弯头处移动，这是由于入口速度增大时，在管道弯头处的发生射流现象而导致弯头处的腐蚀速率增大，由于流体在弯管处是流动速度较大，可以减小流体中颗粒杂志与管道接触面积，所以在弯管与直管段连接腐蚀速率较小。

由数值模拟结果可知，随着管道中流体的入口速度变化，含水率与管道壁面的冲刷腐蚀速率关系曲线如图6所示。

图5 管道冲蚀图

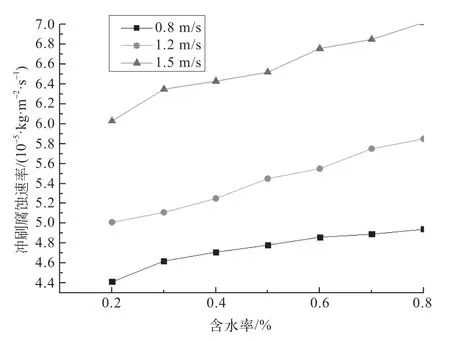
图6 冲蚀速率与含水率关系曲线

由图6可知随着管道的含水率的增大，管道中颗粒杂质的沉降率也增大，且随着速度的增大，管道壁面的腐蚀速率也增大，且在入口速度大于1.2 m/s时管道的受到的冲蚀速率瞬间增大。

2.3 不同的颗粒直径

集输管道中颗粒粒径为100 μm、200 μm、300 μm，入口速度0.4 m/s，含水率为50%。管道的内外壁腐蚀速率如图5所示。

如图7所示管道中颗粒杂质直径的增加会使管道各段的腐蚀速率会发生移动，在出口段会有明显的增加。这是由于管道中固体颗粒杂质的粒径增大，在管道弯头处沉积率逐渐增大，不随油品流动。

图7 管道冲蚀图

数值模拟后发现，颗粒直径对管道管道壁面腐蚀速率关系曲线如图8所示。

图8 粒径与冲蚀速率关系曲线

由上图8可知，颗粒直径在0～100 μm缓慢增加，在100 μm～300 μm时，腐蚀速率急剧增大。在300 μm～500 μm，缓慢增大。产生这种现象的原因是：在0～100 μm时，由于颗粒杂质的不易沉降，裹挟在油品而随着流体流动；粒径在100 μm～300 μm颗粒沉降于管道中，而与管道内表面的接触面积增大；在300 μm～500 μm，由于颗粒粒径比较大，在管道弯头处的沉积率比较高，所以对管道的冲蚀影响反而减小。

3 模拟结果正交分析

弯管中腐蚀速率影响因素正交分析如表1所示。

3.1 结果分析与讨论

对管道的A(入口速度)m/s、B(不同含水率)%、C(颗粒直径)μm研究，假设含有颗粒密度为2 550 kg/m3，入口颗粒质量流量为2.5 kg/s。

3.2 计算Mjm，Mjm ，确定实验因素优组合、优水平

首先分析A因素；把因素A“1”水平放在1、2、3、4号试验中；“2”水平放在5、6、7、8号试验中；

“1”水平KA1=1.16×10-5+4.66×10-5+

“2”水平MA2=3.54×10-5+5.25×10-5+

实验方案及结果分析如表2所示。由上面二元由极差定义公式，可得式(11)，计算各列(包括因素)极差Rj。

表1 因素-水平表

表2 基于交互作用的正交分析

试验极差Rj计算结果见表2，通过对各因素的R值进行比较，通过分析极差大小可知，因素主次为：C(颗粒直径μm)→A×B→A(入口速度m/s)→B×C→B(含水率%)→A×C，通过对表2综合分析可知：各因素对试验指标影响的主次顺序是C＞A＞B；即颗粒直径对试验指标的影响最大，为重要因素；其次是入口速度，影响最小为含水率。效应表可知：C2A1B2(C为颗粒直径μm、A为入口速度m/s、B为含水率%)冲蚀速率最小。

4 结语

通过该次模拟实验研究发现，流体中的颗粒杂质以及混合流体的速度都会影响管道的腐蚀速率，所以在长距离输送管道中，通过一些机械设备的适当的减小管道中流体中的颗粒直径、管道的含水率以及原油乳状液流体的入口速度；或者适当增厚管道弯头与直管段连接处，而增加管道的使用年限，对管道起到防护作用。