基于不同降雨强度的黄土边坡降雨入渗特性研究
2023-03-09关晓迪姚夷凡
关晓迪,姚夷凡
(西安理工大学岩土工程研究所,陕西 西安 710048)
降雨诱发滑坡是中国黄土地区的主要地质灾害之一[1]。据统计,中国已发生的滑坡灾害中,由大气降雨直接或间接诱发的占比90%[2]。然而通常情况下,山体滑坡等自然灾害均伴随着显著的突发性和无预兆性,目前这类灾害还未形成较完善的预警、预报机制[3]。因此,对边坡的降雨入渗特性进行深入研究具有重要的理论和工程实践意义。
在降雨对边坡渗流规律及稳定性的影响方面,大量学者进行了相关研究[4]。在现场边坡降雨试验研究方面,胡明鉴等[5]进行了人工降雨作用的滑坡和泥石流现场试验,模拟了暴雨降雨条件引起的坡面冲刷和垮塌现象,进而引发泥石流的过程,初步探索了蒋家沟暴雨-滑坡-泥石流的共生关系。周中等[6]选取某土石混合体边坡,进行现场降雨试验并同步监测,研究了由降雨入渗引起堆积层边坡失稳的机理以及边坡本身形态随降雨时间变化的特征。张本卓[7]开展了不同降雨强度的尾矿坝边坡现场降雨试验,研究了无植被、有植被以及不同雨强对降雨入渗的影响,得到了雨强、植被、尾矿坝表层渗透系数均对其稳定性有重要影响的结论。徐腾辉[8]通过对贵州某机场的边坡变形监测,归纳总结了高填方边坡变形破坏的影响因素,阐述了其变形破坏机理和破坏模式。
在室内边坡降雨试验研究方面,Geng等[9]通过室内试验模拟了不同降雨强度和坡度梯度对紫壤山坡产沙量的影响,阐明了不同坡度下降雨强度和坡度对总产沙量的贡献率不同,低降雨强度时坡度起主导作用,高降雨强度时降雨强度起主导作用。詹良通等[10]通过对不同雨强下非饱和粉土边坡的失稳过程进行模拟,阐明了降雨引发粉土边坡的发生破坏的过程为局部失稳-向上扩展-整体浅层滑动,得到了雨强同降雨时间的关系曲线。苏燕等[11]结合福建山区典型降雨型滑坡,建立了室内降雨滑坡模型,研究了降雨强度对降雨型滑坡的影响机理。覃小华等[12]模拟了雨水在层状基岩边坡的入渗过程,推导了边坡不同入渗阶段和湿润锋的计算公式,归纳了基岩型层状边坡安全系数的计算公式。王刚等[13]进行了降雨型滑坡室内试验,研究了降雨方式和坡体节理对边坡变形破坏过程的作用,归纳了表层滑坡的诱发机理和破坏模式。
在边坡降雨数值模拟研究方面,武丽[14]通过SEEP有限元模块对不同雨强下边坡入渗进行模拟,分析了雨强、历时、边坡初始孔隙水压力以及土样渗透规律等对边坡渗流场的影响。银晓鹏[15]对降雨型边坡的Saturated/Unsaturated的非稳定渗流问题进行分析,归纳了影响边坡土体孔隙水压力的外在因素,总结了坡比和雨强对边坡稳定性的影响。丁勇[16]量测了不同雨强下坡体的含水量和浸水深度,测定了边坡不同位置的土压力、孔隙水压力和基质吸力,分析了降雨对边坡稳定性的影响。施炳军[17]模拟了降雨作用下边坡渗流场及稳定性问题,研究了降雨和地震共同影响下边坡的破坏机理。蒋水华等[18]以无限长边坡为例,考虑土体饱和渗透系数及抗剪强度参数空间变异性的影响,发展了边坡土体含水率分布和湿润锋深度的修正Green-Ampt入渗模型,探讨了土体多参数空间变异性与降雨入渗相互作用下的边坡失稳机理。
上述模型试验研究成果有益地推进了边坡降雨入渗的研究,但针对不同雨强条件下均质黄土边坡的降雨入渗规律还缺乏系统研究。因此,本文选取甘肃庆阳地区某均质黄土边坡,根据相似比尺原理,建立了室内缩尺模型边坡,开展了不同雨强下边坡降雨入渗试验,对比分析了不同雨强下边坡的入渗特征及坡面冲刷规律。
1 室内模型边坡降雨入渗试验
1.1 试验模型相似比
1.1.1边坡相似比
本文以甘肃庆阳某均质黄土边坡为参照原型,缩尺后进行模型试验,原型边坡的几何特征:坡高4 m,宽2.5 m,坡顶平台长5 m,坡度45°。在尽可能准确、便利地观测模型试验现象和试验数据的前提下,考虑到室内场地的限制,将试验几何相似比设定为原型∶模型=4∶1,即Cl= 4,则模型边坡坡高=1 m。基于相似原理计算出,当密度相似比Cρ=1,重力加速度Cg=1时,几何相似比Cl=n,渗透系数相似比Ck=n1/2,综合各方面因素考虑,将相似比尺设定为n=4,则Ck=2,但在研究过程中发现同时严格满足Cρ=1、Ck=2较难实现,由于降雨入渗的控制因素是土的渗透系数,因此模型土样选取时应以满足Ck=2为首要目标。因此,本文参考原型边坡的黄土干密度ρd=1.55 g/cm3,饱和渗透系数k=2.1×10-6cm/s,根据黄土渗透系数随干密度的变化关系,经过室内物性试验研究,得出了当该类土干密度ρd=1.63 g/cm3时,土样饱和渗透系数位于k=1.0×10-6~1.1×10-6cm/s,此时2种干密度不同的土近似满足Cρ=1,严格满足Ck=2,满足了相似原理的相似条件。因此这里只需在1g重力场中进行缩尺试验,将原型边坡的黄土干密度控制为ρd=1.63 g/cm3来填筑模型边坡,即可解决材料相似问题。表1为原型土和模型土的物性指标对比情况。

表1 原型土和模型土物理力学性质指标对比
1.1.2降雨相似比
当几何相似比设定为Cl= 4时,可以明确降雨历时和降雨强度的相似比均可表示为原型∶模型=2∶1,由于降雨量=降雨强度×降雨历时,因此原型与模型的降雨量相似比为4∶1。本文选取小雨、中雨、大雨、暴雨4种降雨强度研究边坡降雨入渗规律,可以明确模型试验中不同降雨强度的日降雨量,见表2。

表2 原型与模型日降雨量对照 单位:mm
1.2 试验装置
本次试验设备由室内边坡模型箱测试装置、人工降雨装置、试验监测系统组成。人工降雨系统主要包括储水箱、自吸式水泵、控水阀、流量表、一体式实心锥形喷头、PPR降雨管路组成见图1;监测系统由体积含水率监测系统和边坡形态监测系统两部分组成,采用的记录采集仪器分别为水分传感器和数码摄像机。通过室内模拟降雨,测试边坡体积含水率及边坡形态变化情况。
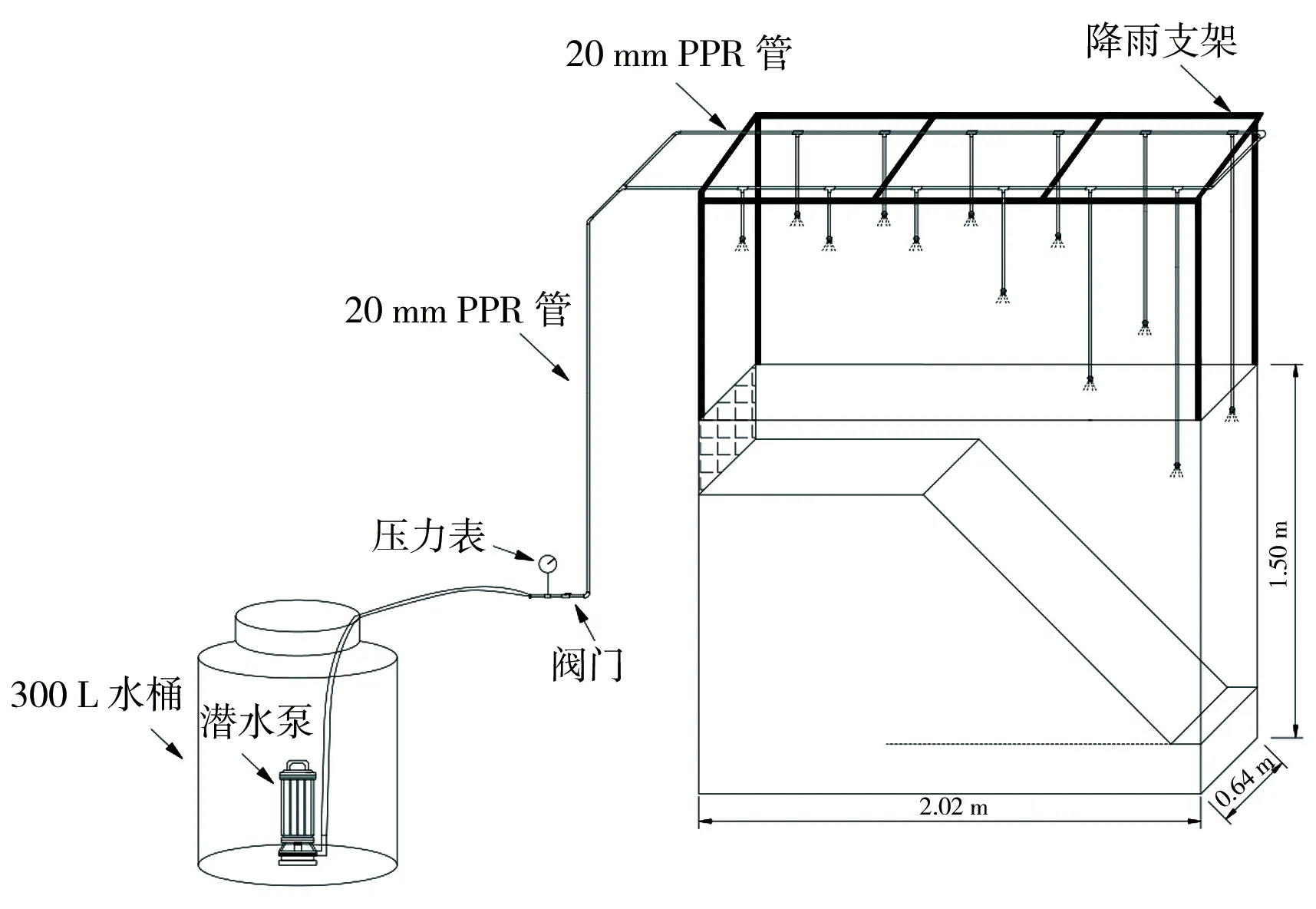
图1 试验系统结构示意
1.3 试验方案
本文选取坡比1∶1的边坡进行4种不同降雨强度(小雨、中雨、大雨、暴雨,持续24 h降雨)的降雨入渗试验,以期对边坡降雨入渗获得规律性的认识,其中不同降雨强度条件下边坡降雨试验的水分传感器埋设见图2。
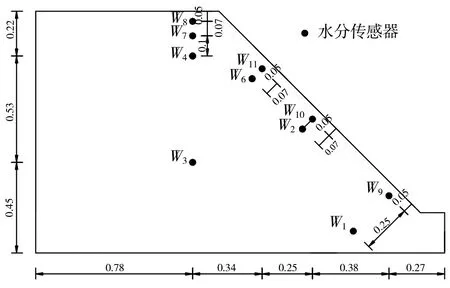
a)小雨
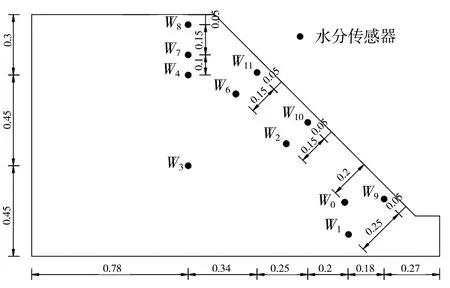
d)暴雨
2 模型试验结果与分析
2.1 体积含水率分析
图3为中雨条件下边坡各测点体积含水率变化曲线。由图可知:试验开始后曲线整体呈上升趋势,曲线陡缓不一,对应的含水率上升幅度和速率各有差异;距坡面同一深度处W8>W9>W11>W10,表明坡顶平台入渗速率最快、边坡中部最慢;且含水率峰值W9max>W8max>W10max,表明坡脚入渗最深、边坡中部入渗最浅,这是由于随着降雨的持续入渗,坡体土层逐渐饱和,基质吸力减小,降雨入渗变慢,越来越多的雨水以径流的形式在边坡表面流失,在坡脚处汇集;降雨结束后,W8、W9、W10、W11均有不同程度的下降,这是蒸发水分散失的作用形成的,而埋设位置较深的W2、W4、W6、W7未出现,说明越深的位置蒸发作用越不显著;降雨过程中,W7处含水率突变点和峰值点的反应时间均明显滞后于W8,说明雨水在黄土体中的运移是由上到下逐渐进行的。
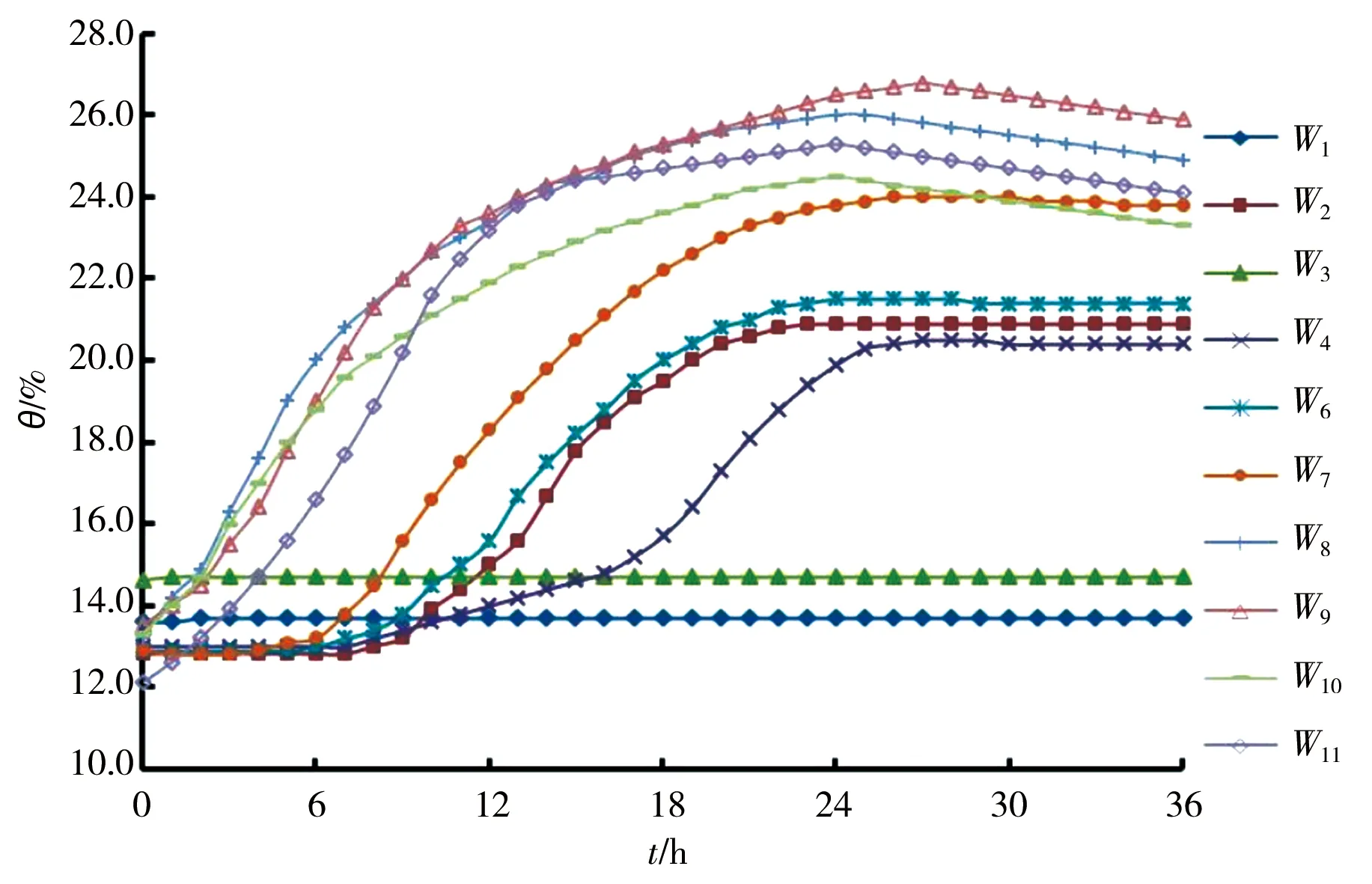
图3 中雨条件下边坡各测点体积含水率时程曲线
图4为不同降雨强度下边坡各测点体积含水率时程曲线。由图可知:在4种雨强下,W1、W2、W3、W6在整个试验过程中含水率无明显变化,说明降雨没有入渗到相应位置,即坡面入渗深度小于75 cm,坡中和坡脚小于20 cm;随着降雨强度的增加,W8和W9的含水率曲线均表现出由缓到陡的趋势,反映了降雨入渗速率随降雨强度的增大而增大;同时在小雨雨强下W8max=24%,W9max=24.5%,在中雨雨强下W8max=25%,W9max=26%,在大雨雨强下W8max=26.3%,W9max=27%,在暴雨雨强下W8max=27%,W9max=28%,说明含水率峰值随着降雨强度的增大而增大,且降雨入渗深度随雨强的增大而增大。
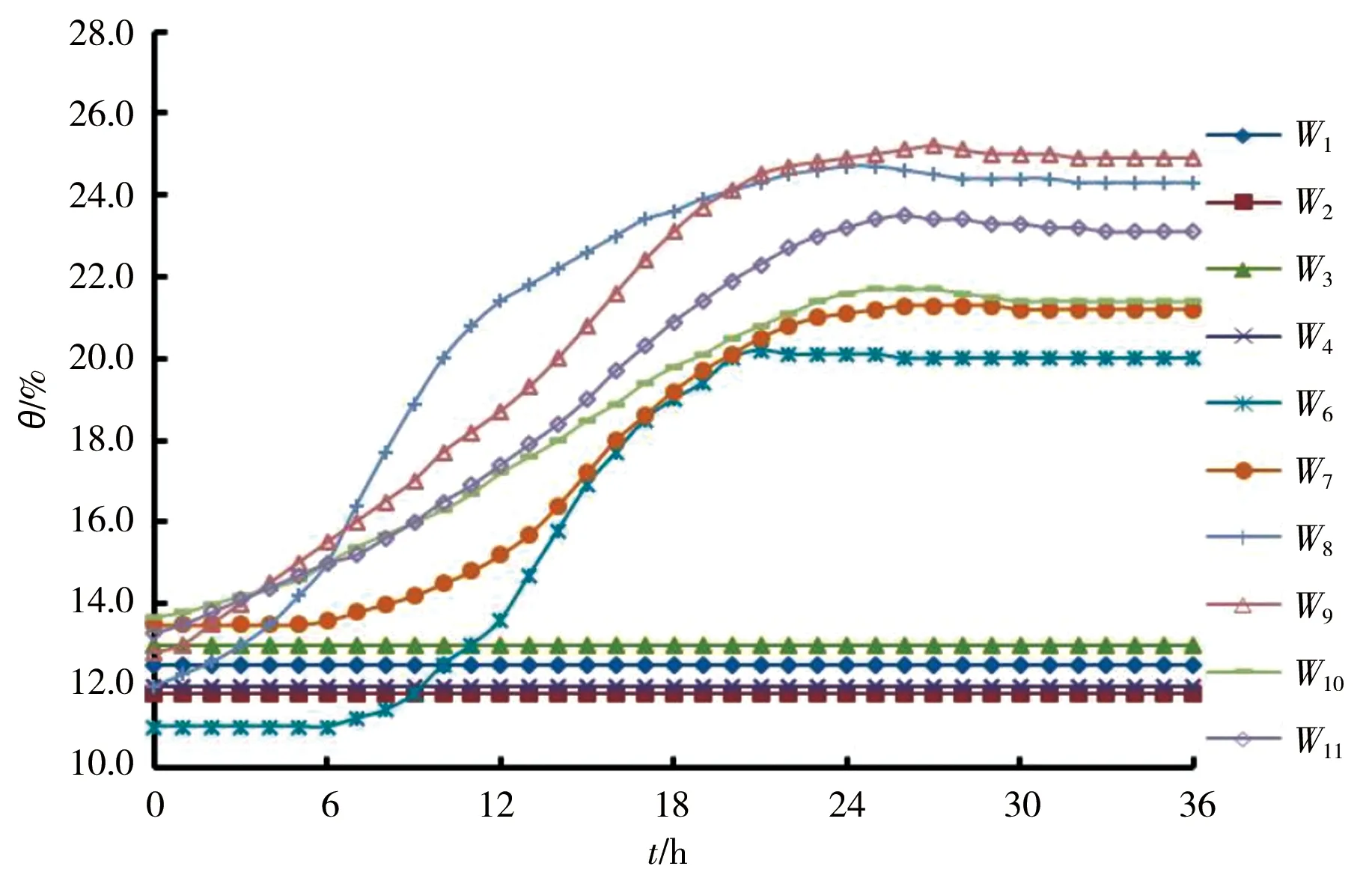
a)小雨
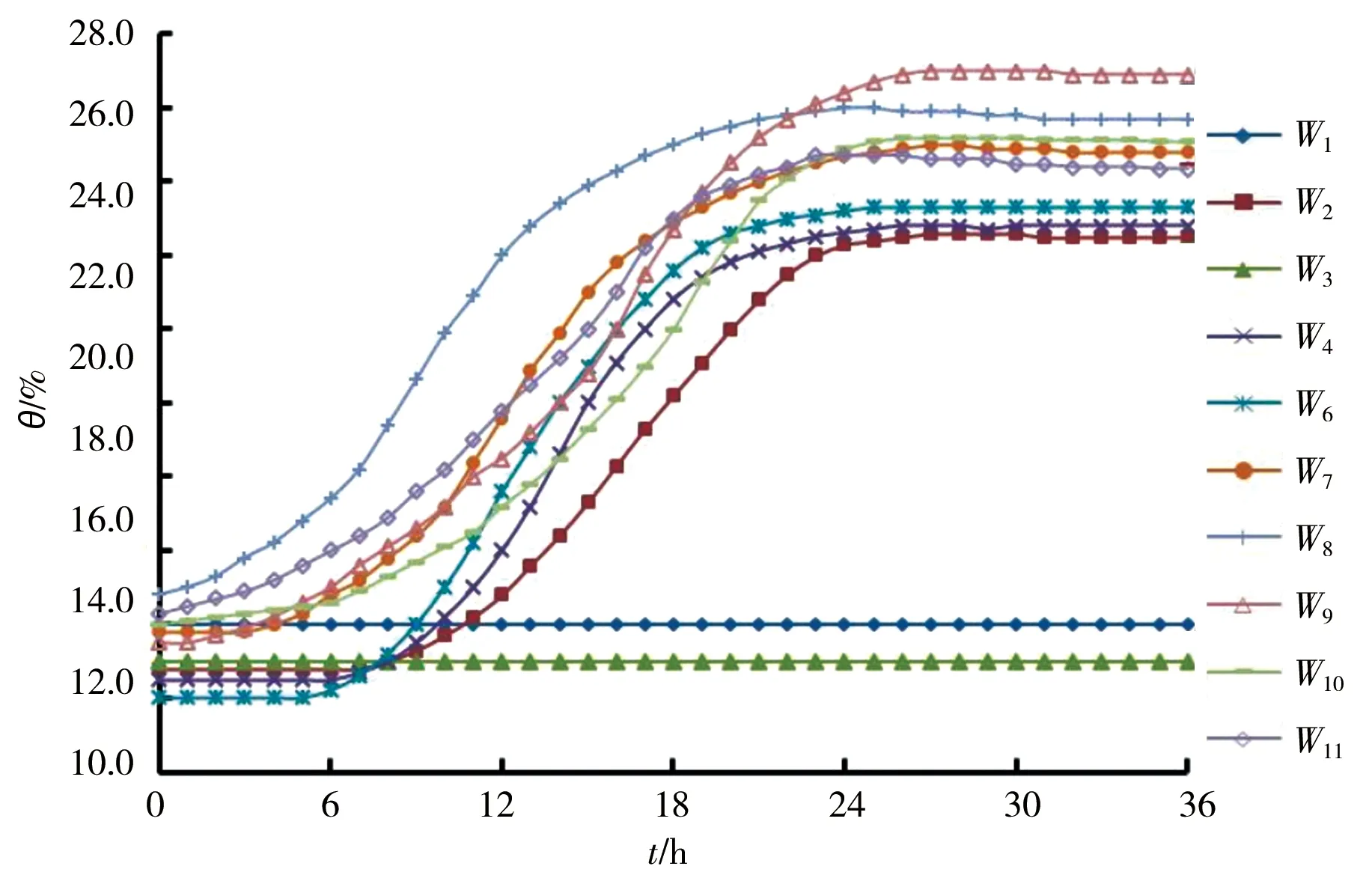
d)暴雨
2.2 湿润锋分析
图5为中雨降雨结束后边坡湿润锋。由图可知:在边坡不同位置处降雨入渗深度有所差异,坡顶平台湿润锋高度在18~23 cm,边坡中部湿润锋高度在15~18 cm,坡脚处湿润锋高度在20~25 cm,说明在边坡不同位置处降雨入渗深度不同,坡脚处最深、坡顶平台次之、坡面中部最浅。

图5 中雨条件下边坡湿润锋
图6为在小雨、中雨、大雨和暴雨雨强作用结束后边坡湿润锋。由图可知:对同一个边坡持续降雨24 h后,不同降雨强度的入渗情况不同;在小雨雨强下,湿润锋高度在10~15 cm;在中雨雨强下,湿润锋高度在15~25 cm;在大雨雨强下,湿润锋高度在18~35 cm;在暴雨雨强下,湿润锋高度在20~40 cm,表明随着降雨强度的增大,降雨入渗深度逐渐加深,但这种加深并不与降雨量的增加成比例。

a)小雨
2.3 冲刷规律分析
图7为不同降雨强度下边坡表面的冲刷现象。由图可知:随着降雨的持续,坡面出现了不同程度的冲蚀破坏,冲蚀作用随着降雨强度的增大而增大;在小雨雨强下雨水充分入渗,坡面无明显径流,亦无冲刷现象;在中雨雨强下坡顶出现局部积水,坡面逐渐形成径流并出现局部土体剥落;在大雨雨强下坡顶和坡面径流明显,坡肩右侧开始出现小部分土体剥落,随着降雨的持续逐渐扩展成沟槽,在冲刷作用下,沟槽变深变宽并沿坡面向下延伸;在暴雨雨强下,坡顶和坡面的径流连结成整体径流,坡顶出现部分浅冲沟,坡面冲蚀程度进一步加大,坡肩右侧产生多条冲沟,强烈的冲刷作用使得冲沟两侧土体迅速塌落,冲沟变深变宽并形成流泥,坡面破坏严重;且在不同降雨强度下,模型边坡各部位的形态变化不同:在小雨雨强下,雨水入渗充分,边坡各部位均未发生变化;在中雨雨强下,坡顶出现局部积水,坡面产生局部径流现象,坡肩小部分土体剥落;在大雨雨强下,雨水入渗极不充分,坡顶和坡面径流明显,坡肩多处土体剥落并形成冲沟;在暴雨雨强下,坡顶和坡面径流连结为整体,边坡破坏明显,坡顶产生部分浅冲沟,坡面冲沟发育充分,土体大面积剥落并产生流泥。

a)小雨
3 边坡降雨入渗数值分析
3.1 数值模型及参数
本文选用饱和/非饱和渗流本构,针对计算模型中非饱和土材料的定义,主要采用非饱和土的渗透特性和SWCC曲线。在非饱和土渗流分析中,基于Geo-Studio有限元软件估计的渗透系数与吸力的关系曲线,见图8。
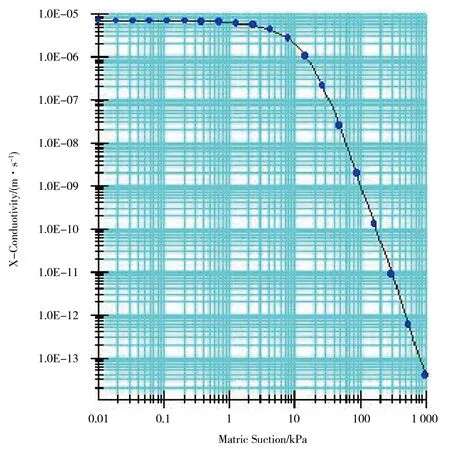
图8 材料渗透系数与吸力的关系曲线
Van Genuchten通过对土水特征曲线的研究,得到非饱和土体积含水率和基质吸力的幂函数形式的表达式为:
(1)
式中θw——计算时段土体体积含水量;θs——饱和含水量;θr——残余含水量;a——进气值函数的土性参数;s——压力水头;n、m——拟合参数。
Van Genuchten模型中的4个参数:θs、θr、a和m对土-水特征曲线的位置、斜率、线型有着较大的影响,其中θs和θr与土本身的性质及类型有关,m决定土-水特征曲线的斜率,a影响SWCC的位置。本次数值模拟中,选取a=20 kPa,n=2,则m=0.5,此时黄土边坡的土-水特征曲线见图9。
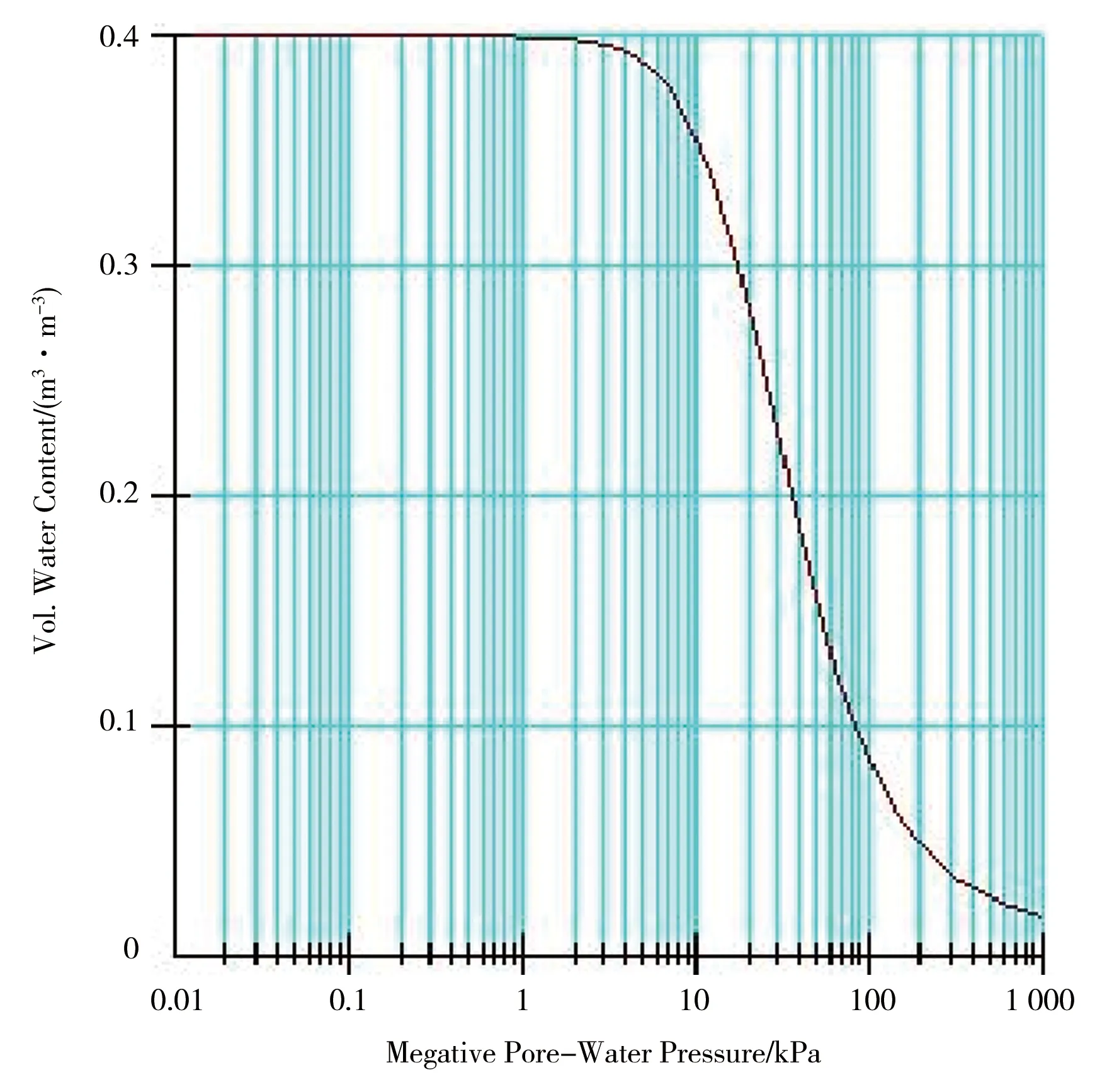
图9 坡体土-水特征曲线
基于采用Geo-studio软件建立相应的数值模型,来分析边坡降雨入渗规律,其中数值模型的边界条件见图10。设置降雨条件为边界条件,以降雨强度的方式作用于边坡上表面,日降雨量分别为1.24E-007 m/s(小雨)、8.1E-008 m/s(中雨)、1.24E-007 m/s(大雨)和1.88E-007 m/s(暴雨),降雨时长为24 h。设置模型底面为零压力线。
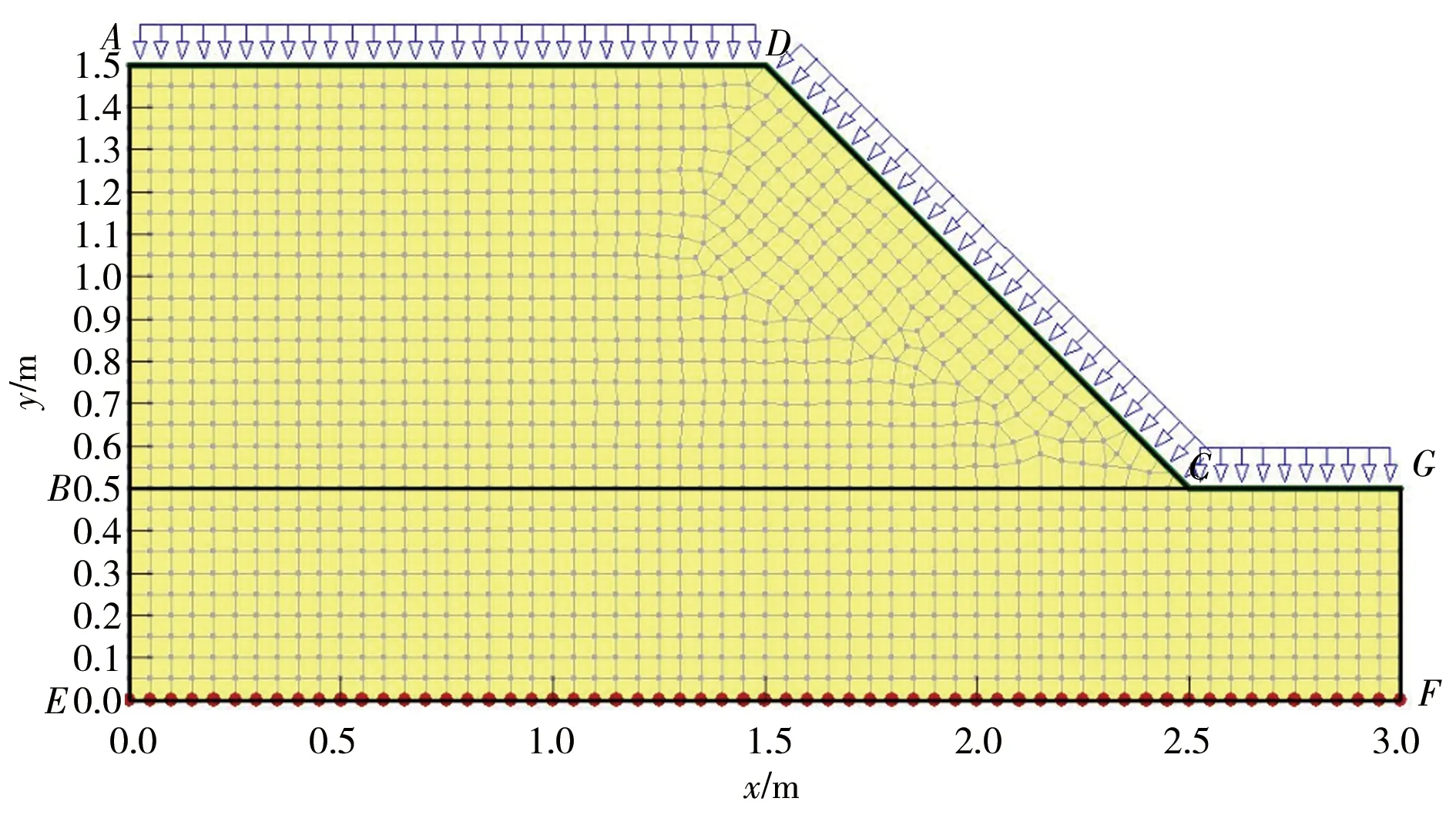
图10 数值模型的边界条件
3.2 模拟结果分析
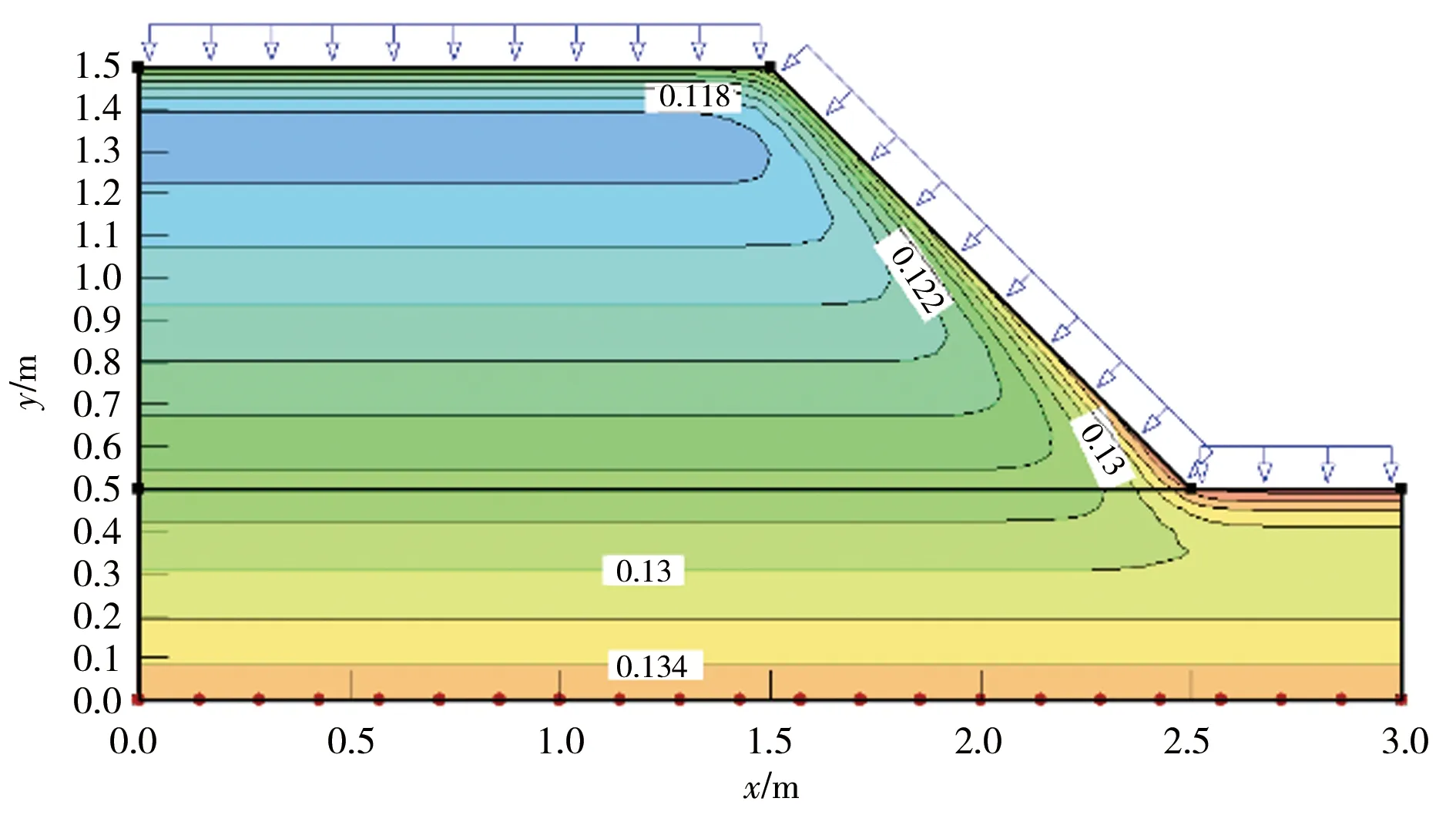
图11为在中雨雨强下边坡不同时刻(6、12、24 h)的体积含水率云图。由图可知:体积含水率变化最显著的区域分布在沿坡体表面向下10~25 cm附近,总体上在坡脚、边坡平台、坡中3个位置的含水率是依次递减的,说明坡脚处降雨入渗程度最快、坡中最慢;且坡顶平台处等势线最密集,坡脚处较坡中稍密集,说明坡顶平台的降雨入渗速率最快,坡脚处稍慢,这与模型试验中在边坡不同位置的降雨入渗规律是一致的;从图中3个时刻标记的体积含水率数值可以发现:坡顶平台处含水率分别为12.2%、13.5%、15.0%,坡脚处含水率分别为13.4%、13.5%、15.5%,坡中处含水率分别为12.2%、13.0%、14.5%,说明随着降雨历时的增长,相同位置土体含水率逐渐增大,降雨入渗是逐渐进行的过程。
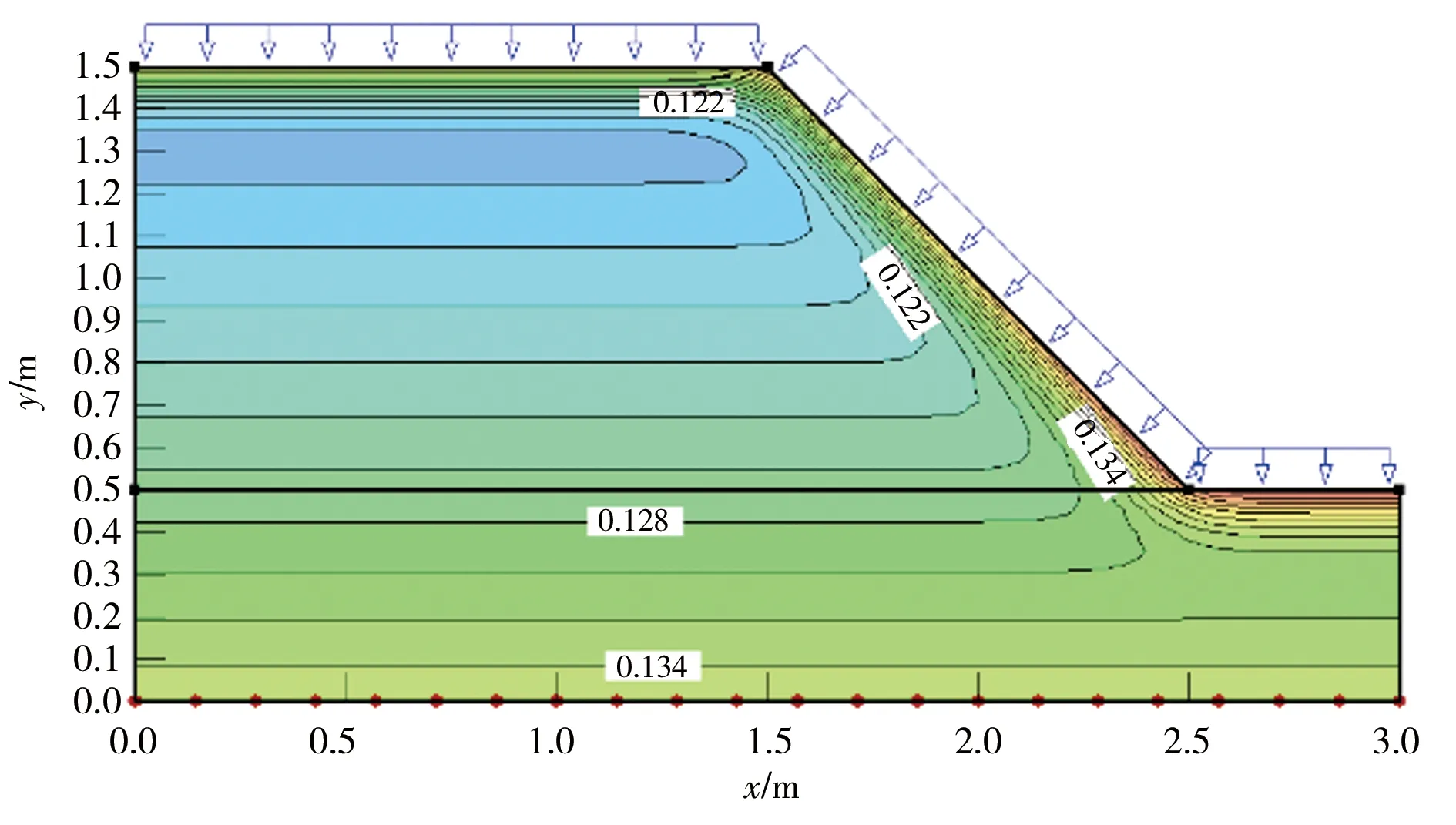
a)降雨6 h时刻
中雨雨强下数值模型各测点体积含水率时程曲线见图12,WSn表示数值模拟中相应位置处含水率,图13为中雨雨强下模型试验中边坡各测点体积含水率时程曲线。由图可知:在降雨开始后,埋深均为5 cm的测点WS8、WS11、WS10和WS9含水率增大,降雨24 h含水率达到最大值,之后在蒸发作用下含水率有减小趋势;降雨结束后的3 h内,坡脚埋深5 cm处WS9含水率仍保持上升趋势,这是坡体内部水在重力作用下逐渐向下运移的结果,这与模型试验得出的结论一致;降雨过程中,WS8含水率最先发生变化且曲线最陡,说明坡顶平台的降雨入渗速度最快;且埋深12 cm的WS7在降雨开始5 h后增大,WS6在降雨7 h增大,WS2在降雨开始8 h后逐渐变化,反映了坡顶平台的入渗速率大于坡面,这与模型试验的入渗速率规律一致;坡脚处埋深30 cm处WS1在降雨开始后逐渐增大,说明坡脚处的入渗深度达到了30 cm,而WS4含水率的变化说明坡顶平台的入渗深度达到了20 cm,这与模型试验时,浸润线的分布情况大致相同。
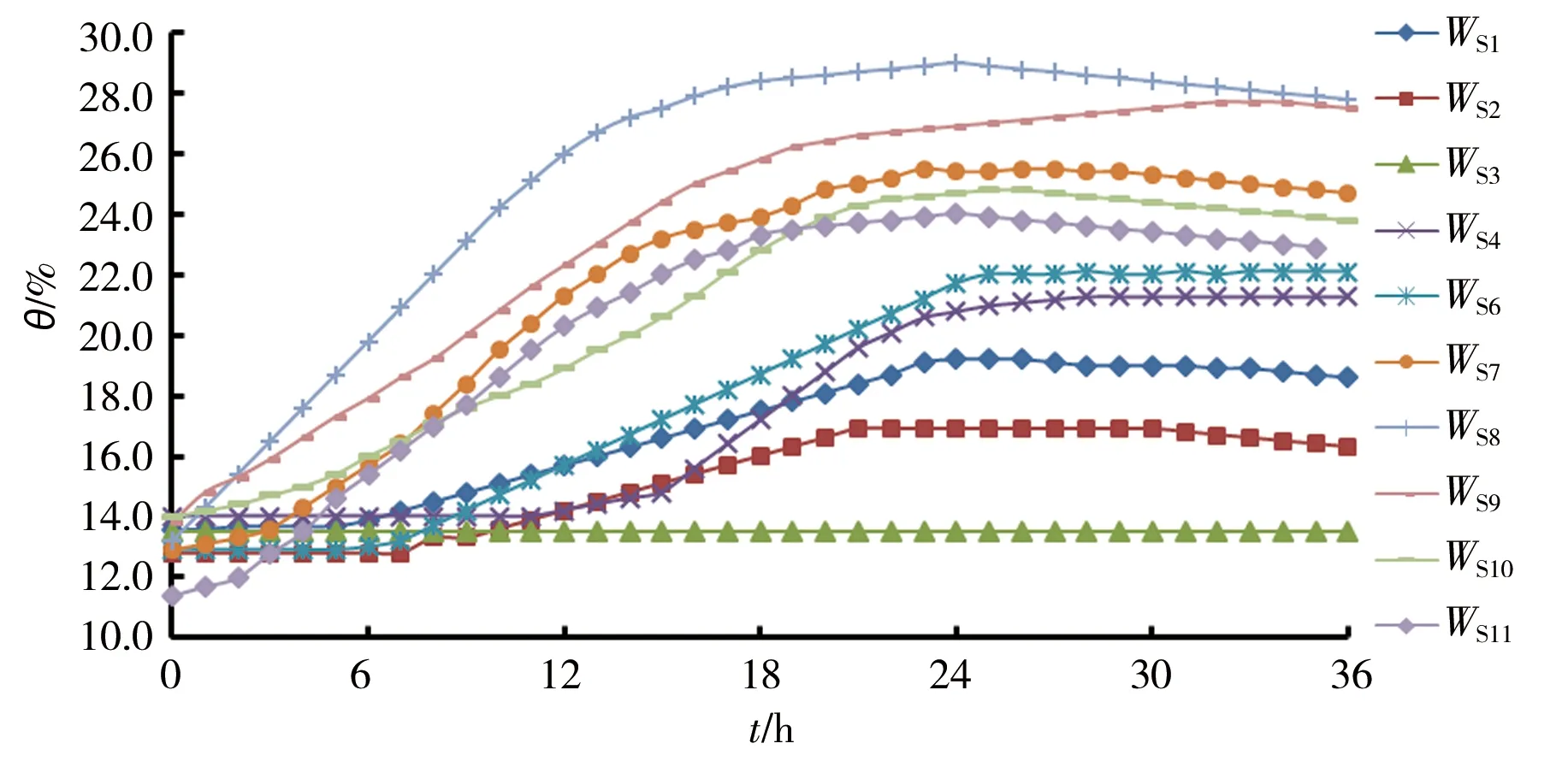
图12 数值计算中坡比1∶1的边坡体积含水率随时间的变化
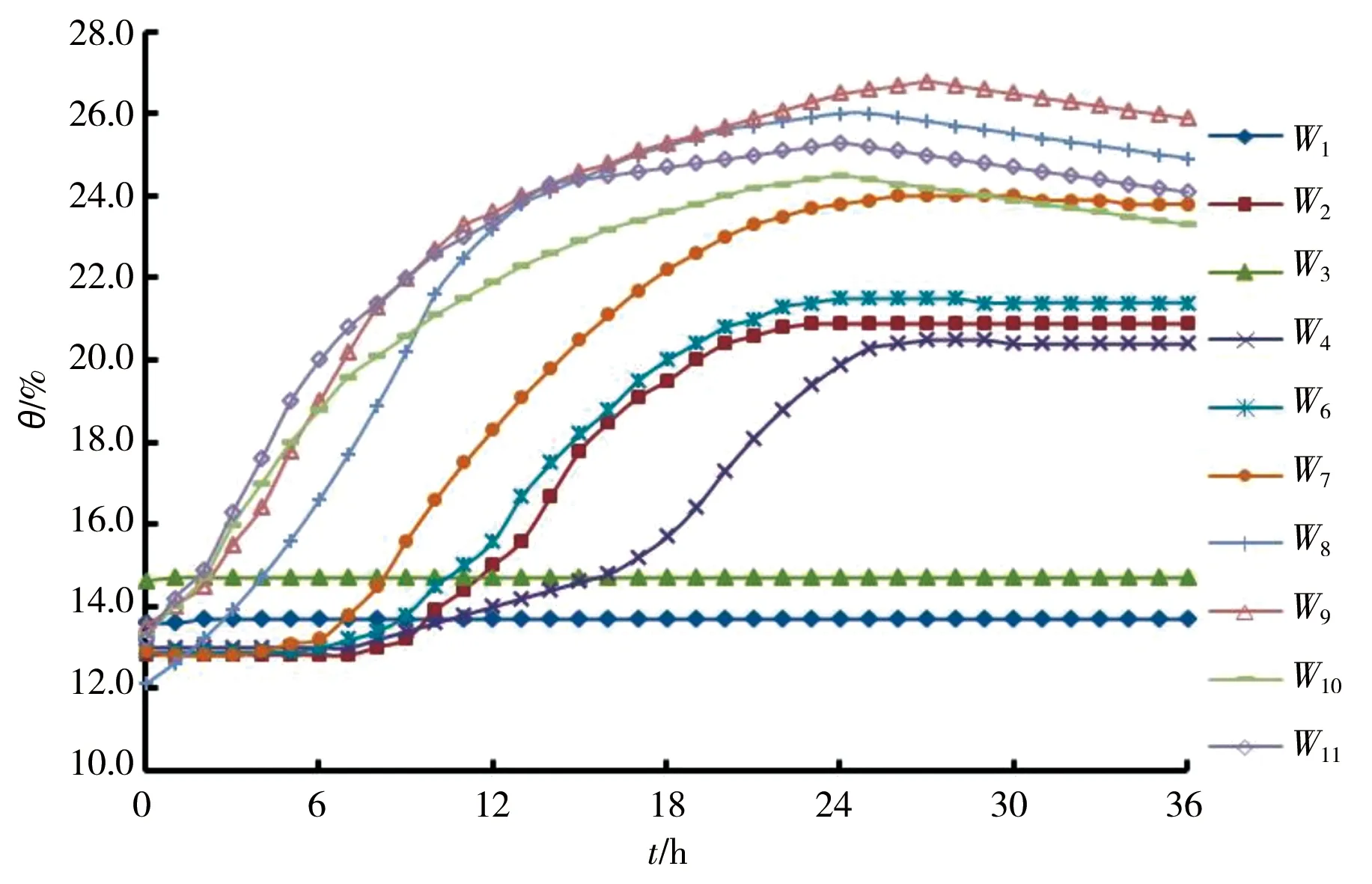
图13 模型试验中边坡体积含水率随时间的变化
图14为在小雨、中雨、大雨、暴雨4种雨强下降雨6 h时的边坡体积含水率云图。由图可知:在4种雨强下坡顶平台处土体的含水率分别为11.8%、12.6%、13.0%和14.0%,坡中处土体的含水率分别为12.2%、12.4%、13.0%和13.5%,坡脚处土体的含水率分别为13.0%、13.6%、14.0%和14.5%,可以发现随着降雨强度的增大,相同位置边坡土体含水率也随之增大,但不同雨强间增幅略有差异,含水率的增长与雨强之间没有绝对的线型关系,这与室内模型试验得出的不同雨强对边坡降雨入渗规律影响的结论一致。
a)小雨
在分析不同降雨强度对降雨入渗的影响时,选择边坡中部10 cm深度位置处WS10的数据变化进行分析,不同降雨强度下WS10的含水率时程曲线见图15,图16是模型试验中不同降雨强度下W10随时间变化的曲线。由图可知:降雨强度越大,曲线越陡,边坡含水率变化响应时间越短,降雨结束后的含水率越大,说明随着降雨强度的增大,降雨入渗速率和入渗深度都在变大,这与模型试验得出的结论一致。
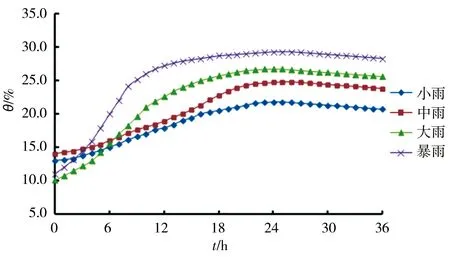
图15 不同降雨强度下体积含水率随时间的变化
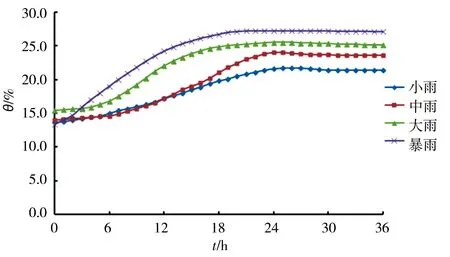
图16 模型试验中不同降雨强度下体积含水率随时间的变化
4 结论
本文以甘肃庆阳某自然黄土边坡为参照原型,根据相似原理,在室内建立了满足相似前提条件的模型边坡,进行了不同雨强下的边坡降雨入渗试验,同时利用有限元软件Geo-Studio中的SEEP/W模块建模进行仿真计算,得到了不同降雨强度条件下降雨入渗规律和冲刷规律,主要结论如下。
a)24 h持续模拟小雨条件下,边坡降雨入渗深度在10~15 cm;24 h持续模拟中雨条件下,入渗深度在15~25 cm;24 h持续模拟大雨条件下,入渗深度在18~35 cm;24 h持续模拟暴雨条件下,入渗深度在20~40 cm。
b)同一工况中,降雨10~12 h时,降雨入渗速率显著增大,随着降雨的持续,土体逐渐饱和,降雨入渗速率逐渐减慢,降雨结束时刻减小为0,之后在蒸发作用下呈微妙的负增长趋势。
c)在边坡不同位置处降雨入渗速率不同,表现为坡顶入渗速率最快、坡脚较快、边坡中部最慢;在边坡不同位置处降雨入渗深度亦不同,表现为坡脚入渗深度最大、坡顶较大、边坡中部最小。
建议:研究可为西北地区自然黄土边坡防护和降雨型滑坡治理提出建设性意见,可以明确的是,边坡坡脚和坡顶平台是降雨活动中最脆弱的部分,需要做特别覆盖措施或引流措施。
