FBG在温度交变环境下温度灵敏度研究

庞 博，赵 峥，周月阁，刘守文,2

FBG在温度交变环境下温度灵敏度研究

庞 博1，赵 峥1，周月阁1，刘守文1,2

（1. 北京卫星环境工程研究所，航天机电产品环境可靠性试验北京市重点实验室，北京，100094；2. 可靠性与环境工程技术重点实验室，北京，100094）

为探求FBG在太空温度交变环境下是否可靠，建立了温度灵敏度试验系统。研究温度变化引起光纤光栅波长漂移与热膨胀系数之间的关系。首先，搭建光纤光栅温度敏感检测试验平台，通过改变环境温度获取FBG光谱并与理论漂移系数进行了对比，然后，建立温度与FBG主波长的线性与二次多项式拟合关系并选取SSE、RMSE、R-square三个指标对比两种拟合方法的优劣，最后分析了理论计算与试验计算结果差异的原因。试验结果表明，在温度设定的范围-60℃到110℃作为外层空间温度的模拟温度环境下，理论温度漂移值与实际值在不同光栅位置分别有7.4%、7.7%的误差，故FBG由于温度变化的主波长偏移用二次多项式拟合比理论相对线性拟合更精确。从而，利用FBG的机械参数来计算FBG的温度敏感系数是不合适的，具体的温度敏感系数需要通过试验来确定。

温度敏感性；FBG；主波长

0 引 言

光纤光栅传感器技术是具有广泛应用前景的传感器技术。近年来被广泛应用于监测航空结构和材料的健康状态[1,2]。相比于大多数其他传感器，如PZT[3]、ICMS，FBG[4]传感器有轻量级和波分复用等许多优点。

一般来说FBG的响应是由温度和应变耦合而决定的，主波长位移在平均应变范围内是线性的[5]，然而，对于FBG的温度响应，主波长的变化要复杂得多。基于理论和试验分析，学者们对FBG的温度灵敏度进行了大量的研究。Wolfgang Eche等[6]提出了一种由 12个FBG组成的分布式网络传感系统来监测X-38航天器的结构健康，温度范围为-40 ℃～200 ℃、应力范围为-1000 με～3000 με。

在试验中独立考虑FBG的温度敏感性，排除了应变效应的影响，使FBG处于无应力状态。当FBG处于低温状态时，FBG的温度灵敏度变得更加非线性。此外，主波长随温度每增加5 ℃，性能的漂移相比于理论相对线性拟合更符合二次多项式拟合。

1 试验设计

本文中，测量布拉格波长偏移来确定作用在光栅截面上的温度效应。搭建了光纤光栅温度敏感检测试验平台，主要分为温度控制系统和光学传感系统（SM125）两大部分。为了模拟外太空船的温度环境，温度范围设定在-60 ℃～110 ℃之间，其升温间隔为5 ℃。为了获得温度灵敏度，通过温箱实现对温度的控制，4个FBG传感器在无应力状态下平行放置在其中。此外，这里使用光学传感系统（SM125）来获得FBG在不同温度下的反射响应。

图1 FBG温度灵敏度检测系统的试验装置

2 结果与讨论

试验评估了在0 ℃、5 ℃下的响应信号，如图2所示。由图2可知，随着温度的升高，主波长变长。

图2 不同温度下的反射光谱

续图2

为了分析在极端环境下主波长漂移与温度变化之间的关系。通过提取光纤光栅的反射率谱，得到了光纤光栅在温度范围-60 ℃到110 ℃梯度5 ℃下的特征。然后，对于每个光栅位置，在该测试中可以处理35组试验数据。如前所述，为了消除随机误差，在温度箱中放置了4个带有8个光栅的FBG。处理结果如图3所示。

图3 FBG1与FBG2在不同温度环境下主波长的变化

图3a和3b所示的圆圈清楚地显示了波长漂移随温度升高的奇异性。这些波长的漂移可能是随机出现的，原因是其他FBG没有显示出相同的性能。因此，利用FBG3和 FBG4来分析灵敏度系数，此外，图中其他部分，主波长漂移与温度的变化曲线并不满足单变量线性回归。那么，它们的系数可能不等于系数理论计算[7]常系数0.01 nm/℃。试验与理论所得的系数存在误差，导致当光纤光栅材料随热膨胀、随冷收缩时[8]，光纤光学性能和力学性能经历不同的温度阶段时会发生不可预测的变化。

下面，对FBG3与FBG4分别进行了主波长和温度之间的线性和二次拟合。为了评价两种拟合方法的性能，这里选择误差平方和（SSE）、确定系数（R-square）和均方根误差（RMSE）这3个指标[9]来定量拟合性能。

2.1 线性模型拟合

通过对FBG3与FBG4各组光栅的数据进行线性拟合得到的数据如图4、图5所示。

图4 FBG3主波长与温度的线性回归拟合结果

表1 FBG3拟合结果的公式及评价指标

Tab.1 The Function and The Evaluation Indicators of the FBG3 Fitting Results

数据指标光栅位置1光栅位置2 拟合结果公式F(X)=0.01074X+1465F(X)=0.01075X+1466 误差平方和0.01760.0177 确定系数0.99820.9983 均方根误差0.023150.02316

图5 FBG4主波长与温度的线性回归拟合结果

表2 FBG4拟合结果的公式及评价指标

Tab.2 The Function and The Evaluation Indicators of the FBG4 Fitting Results

数据指标光栅位置1光栅位置2 拟合结果公式F(X)=0.00923X+1472F(X)=0.00922X+1471 误差平方和0.019310.01932 确定系数0.99740.9975 均方根误差0.02410.0242

表1、表2中给出了主波长随温度的线性拟合结果。FBG温度灵敏度理论值为0.01 nm/℃，以第1个光栅为例，拟合结果中FBG3的温度灵敏度为0.01074，FBG4的温度灵敏度为0.009 23，通过计算与理论值的相对误差，结果如下：

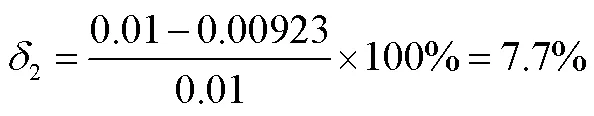
通过计算相对误差得到的误差结果较大，此外，从45 ℃到100 ℃，灵敏度系数不符合线性计算结果。当温度低于-40 ℃时，曲线几乎不平滑，即显示温度敏感性有波动。

2.2 二次拟合方法

为了选择合适的拟合方法解决上述线性拟合中的问题，本文提出了二次拟合方法。FBG3和FBG4的处理结果如图6、图7和表3、表4所示。

图6 FBG3主波长与温度之间的二次回归拟合结果

表3 FBG3二次拟合结果公式及评价指标

Tab.3 The Function and The Evaluation Indicators of the FBG3 Quadratic Regression Fitting Results

数据指标光栅位置1光栅位置2 拟合结果公式F(X)= 9.514 e-06*X2+ 0.01055*X+1529F(X)= 9.513 e-06*X2+ 0.01056*X+1529 误差平方和0.0060150.006016 确定系数0.99940.9993 均方根误差0.013710.01372

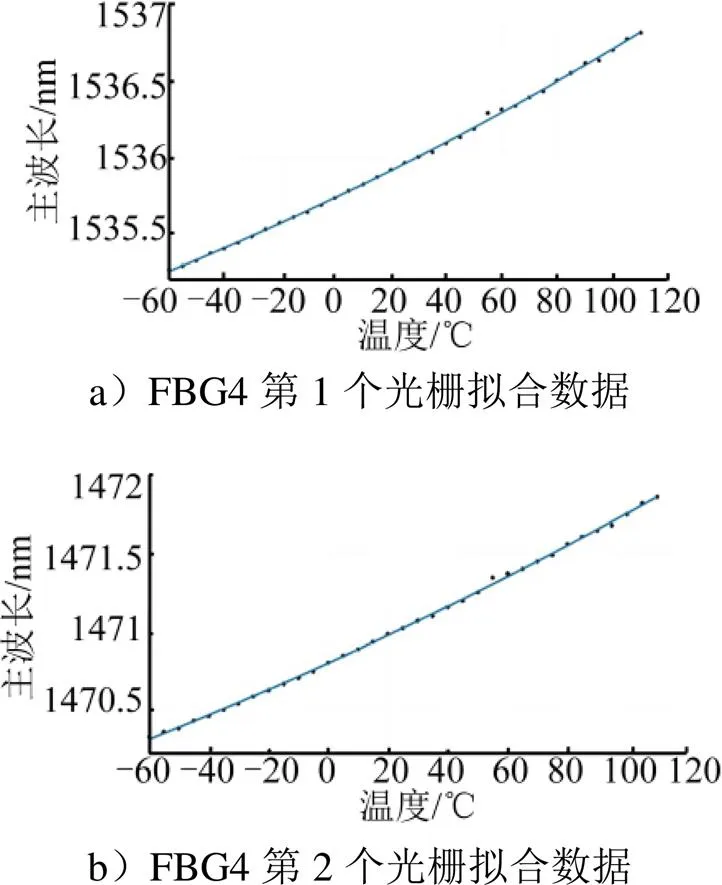
图7 FBG4主波长与温度之间的二次回归拟合结果

表4 FBG4二次拟合结果公式及评价指标

Tab.4 The Function and The Evaluation Indicators of the FBG4 Quadratic Regression Fitting Results

数据指标光栅位置1光栅位置2 拟合结果公式F(X)=7.132e-06*X2+ 0.01016*X + 1534F(x) =7.131e-06*X2+ 0.01017*X+ 1534 误差平方和0.0097370.009735 确定系数0.9990.999 均方根误差0.017440.01743

通过对FBG3和FBG4数据处理的理论线性拟合方法和二次拟合方法的比较。可以看出从45 ℃到100 ℃，二次拟合的灵敏度系数比线性拟合结果更准确。当温度低于-40 ℃时，二次拟合结果相较于线性拟合结果也更平滑。

通过对SSE、R-square和RMSE的计算，也显示相比于线性拟合二次拟合的SSE与RMSE更小，R-square更大，证明了二次拟合的性能优于线性拟合方法。同时，通过对波长偏移量与曲线中的温度进行线性拟合，发现二者之间的线性关系是一个近似函数，恒温灵敏度系数表示在一定温度范围内温度灵敏度系数的平均值。当温度增加超过45 ℃时，随着温度的逐渐升高，FBG的温度敏感系数迅速增大，因此，用于拟合相对主波长漂移和温度的二次关系比线性拟合法具有更好的效果。

光纤光栅温度灵敏度的理论计算值与试验值之所以存在差异，是因为理论值是通过光纤光栅材料的力学参数得到的。但在试验中，在温差交替作用下，原有的折射率、温度系数等机械参数发生了改变。导致主要基于上述两个光纤参数的温度敏感系数将发生变化。在实际应用中，如果使用FBG来精确测量温度，利用FBG的机械参数来计算FBG的温度敏感系数是不合适的，具体的温度敏感系数需要通过实验来确定。

3 结束语

本文对不同温度值下的光纤光栅响应信号进行了处理，确定了FBG的温度灵敏度。与理论线性拟合方法相比，二次拟合模型具有最小的SSE和最小的RMSE，此外R-square最大。通过对线性拟合结果与实验二次拟合结果误差的分析，造成差异的原因是FBG感知温度梯度时FBG材料随热膨胀，随冷收缩。FBG反射光谱随FBG折射率和温度系数的变化而变化，所以单纯的线性拟合方法不能准确地反应FBG的温度灵敏曲线。

[1] Chai Q, et al. Spectral characteristics of rotated fused polarization maintaining fiber Bragg gratings subjected to transverse loading[C]. Jeju Island: International Conference on Optical Fiber Sensors, 2017.

[2] 高扬, 等. 基于光纤耦合金刚石NV色心系综磁强计的电路诊断方法[J]. 航天器环境工程, 2022, 39(1): 100-104.

GAO Yang, et al. The circuit diagnosis method with diamond NV center ensemble magnetometer based on fiber coupling[J]. Spacecraft Environment Engineering, 2022, 39(1):100-104.

[3] Ogisu T, Okabe Y, Takeda N. Development of damage monitoring system for aircraft structure using a PZT actuator/FBG sensor hybrid system[J]. Proceedings of SPIE - The International Society for Optical Engineering, 2004, 5388(10): 53-54.

[4] 田园, 薛雅心. 光纤光栅光谱异常模式判别和自适应分段拟合在温度标定中的应用[J]. 航天器环境工程, 2021, 38(4): 472-479.

Tian Yuan, Xue Yaxin. Application of FBG spectrum abnormal pattern diagnosis and adaptive piecewise fitting in temperature calibration[J]. Spacecraft Environment Engineering, 2021, 38(4):472-479.

[5] Chen Y, et al. Load location and measurement system based on fiber Bragg grating sensor[J]. Journal of Mechanical Engineering, 2016, 52(18): 8-15.

[6] Ecke W, et al. Optical fiber grating sensor network based on highly reliable fibers and components for spacecraft health monitoring[J]. Proc Spie, 2001(4328): 297-305.

[7] Wu M C. Pressure effects on the temperature sensitivity of fiber bragg gratings[C]. Hampton: American Institute of Physics, 2013.

[8] Abtahi M, et al. Characterization of a linearly chirped FBG under local temperature variations for spectral shaping applications[J]. Journal of Lightwave Technology, 2011, 29(5): 750-755.

[9] Tong H. Convergence rates for empirical bayes estimators of parameters in linear regressin models[J]. Communications in Statistics, 1996, 25(6): 1325-1334.

Study on the Temperature Sensitivity of FBG under the Condition of Temperature Alternation

Pang Bo1, Zhao Zheng1, Zhou Yue-ge1, Liu Shou-wen1,2

（1. Beijing Institute of Spacecraft Environment Engineering Beijing Key Laboratory of Environmental and Reliability Testing for Aerospace Mechanical and Electrical Products, Beijing, 100094; 2. National Key Laboratory of Science and Technology on Reliability and Environmental Engineering, Beijing, 100094)

In order to explore whether FBG is reliable in the space temperature alternate environment, a temperature sensitivity experimental system is established. The relationship between wavelength shift and thermal expansion coefficient is studied. First of all, the fiber Bragg grating temperature sensitive detection experiment platform is set up, and then, by changing the environment temperature for FBG spectrum and drift coefficient is compared with theory, and then temperature with FBG wavelength of linear and quadratic polynomial fitting relations are established and SSE, RMSE, R-square three index contrast the merits of the two fitting methods, finally the reason for the difference between the theoretical calculation and experimental results are analyzed. Experimental results show that the temperature setting of the range to -60℃ to 110℃ as the temperature of the outer space simulated temperature environment, the theory of temperature drift value and actual value in different error of the grating position are 7.4%, 7.7%, so the FBG main wavelength shift due to temperature changes with a quadratic polynomial fitting are more accurate than the theory of relative linear fitting. Therefore, it is not appropriate to use the mechanical parameters of FBG to calculate the temperature sensitivity coefficient of FBG. The specific temperature sensitivity coefficient needs to be determined through experiments.

temperature sensitivity; FBG; primary wavelength

2097-1974(2023)01-0088-05

10.7654/j.issn.2097-1974.20230118

TP394.1；TH91.9

A

2019-02-19；

2019-06-03

庞 博（1993-），男，工程师，主要研究方向为航天器用通信传输光纤可靠性。

赵 峥（1985-），男，技师，主要研究方向为航天器组件级单机产品真空环境可靠性。

周月阁（1986-），男，博士，高级工程师，主要研究方向为机电产品环境与可靠性。

刘守文（1975-），男，博士，研究员，主要研究方向为航天器环境与可靠性试验技术。