涡轮盘疲劳寿命可靠性设计仿真及优化策略*

2023-03-09张文鑫吕震宙

国防科技大学学报 2023年1期

张文鑫，吕震宙

(西北工业大学航空学院，陕西西安 710072)

涡轮盘是航空发动机主要部件之一，在高温、高速下工作，所承受的载荷复杂，所处的环境严酷，一旦发生破坏性故障将导致严重的后果。在涡轮盘的实际工作环境中，有许多影响涡轮盘疲劳寿命的因素具有随机不确定性[1-2]，如模型尺寸参数、材料参数、边界条件等，这些随机不确定性因素导致涡轮盘疲劳寿命也具有随机不确定性。随着航空发动机的发展，涡轮盘工作时的温度和转速提高，如何在保障安全的条件下提高涡轮盘的疲劳寿命就显得尤为重要。因此，有必要开展涡轮盘疲劳寿命可靠性优化设计，这对于保证发动机正常、稳定、安全的运行具有重要意义。

涡轮盘的疲劳寿命可靠性优化设计的难点主要在于涡轮盘有限元分析过程复杂，一次结构有限元静力分析都会耗费较长的时间，而进行疲劳寿命可靠性分析时需要进行大样本量的结构分析，这将导致涡轮盘疲劳寿命可靠性优化设计中约束函数的处理会非常费时，进而导致优化求解的效率低下[3-5]。

基于代理模型法的优化算法是一类高效求解可靠性优化设计的算法。由于自适应构建可靠性优化设计中隐式目标和约束函数的代理模型所需的训练样本点集规模远小于备选样本点集规模，因此基于代理模型法的优化算法是一种求解疲劳寿命可靠性优化的高效方法[6-9]。许多文献[10-14]都使用了基于代理模型法的优化算法求解涡轮盘疲劳寿命可靠性优化问题。文献[10]基于响应面法近似模型和模拟退火法寻优技术，以涡轮盘的强度和疲劳寿命可靠性为约束，以质量最小为目标函数，对涡轮盘进行了优化，减轻了其质量。文献[11]在涡轮盘疲劳寿命可靠性优化模型中，将双辐板轮盘盘心、榫槽寿命可靠性优化的过程简化为基于应力约束的寻优过程，然后通过构造代理模型使用确定性优化算法进行可靠性优化模型求解。文献[12]基于响应面法近似模型，以结构强度和疲劳可靠性作为约束，以质量最小为目标函数，采用随机优化方法对轮盘进行优化设计。文献[13]利用Kriging模型以及多岛遗传算法对涡轮叶片进行多学科优化设计。文献[14]利用响应面模型以及多目标遗传算法对发动机的多工况性能进行可靠性优化设计。

使用基于代理模型法的优化算法求解可靠性优化问题的核心是代理模型构建的精确性，这关系到了可靠性优化模型求解的精度。在构建功能函数代理模型来估计失效概率时，训练点的分布对失效概率估计值的精度有着重要的影响。文献[10-14]均在整个输入变量空间中选取训练点，依据这些训练点生成代理模型。但是这样构建的代理模型一般较难满足失效概率估计的精度要求，原因在于这些方法生成的训练样本点均布于整个输入变量空间中，而失效域边界附近的训练样本点数量不多，因此可能导致失效概率估计不准确。为解决该问题，自适应选取训练点的策略被提出[15]。该策略采用学习函数有“目的”地从备选样本池中选择新的训练点，添加到代理模型的训练点集中，使训练点更多地集中在失效概率估计感兴趣的失效域附近，从而更准确地估计失效概率。这类自适应构造代理模型与数字模拟结合来估计失效概率的方法，称为数字模拟结合代理模型的方法[15-19]。

本文将针对涡轮盘的疲劳寿命可靠性优化设计这一工程问题，设计了涡轮盘高低周复合疲劳寿命可靠性优化设计的联合仿真平台，仿真平台使用基于代理模型法的优化算法求解可靠性优化问题。本文所提出的优化算法包括两点技术创新：其一是利用寿命函数和寿命可靠性分析极限状态函数中的共性需求，提出了在优化迭代的过程中自适应构建寿命函数Kriging模型和寿命可靠性极限状态面Kriging模型时共用训练样本点的策略；其二是提出了一种构建寿命函数Kriging模型的SVDM学习函数。

1 涡轮盘疲劳寿命可靠性优化设计仿真框架

涡轮盘疲劳寿命可靠性优化设计过程涉及多个软件，包括使用Solidworks构建涡轮盘参数化模型，使用ANSYS进行涡轮盘有限元分析，以及使用MATLAB运行可靠性优化算法。本文使用MATLAB建立控制平台，整个涡轮盘疲劳优化设计仿真由仿真输入、有限元分析、疲劳寿命计算、疲劳寿命可靠性优化设计以及优化结果组成，仿真平台各部分的关系如图1所示。

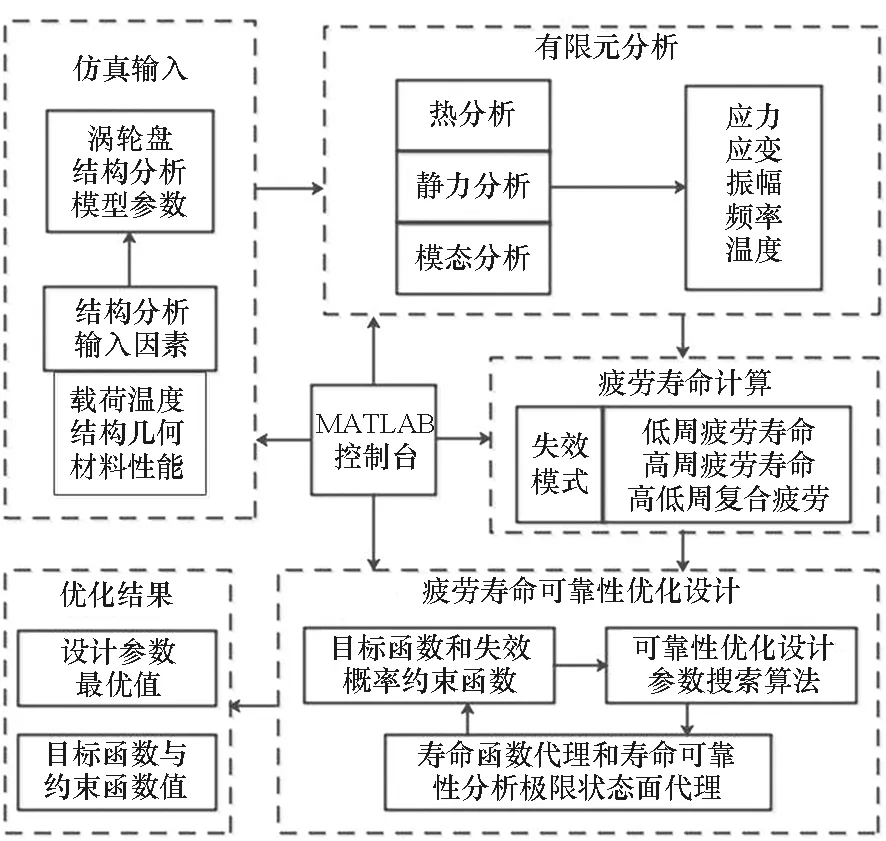
图1 涡轮盘疲劳寿命可靠性优化设计联合仿真平台Fig.1 Co-simulation platform of reliability optimization design for turbine disk′s fatigue life

仿真输入部分主要功能为由MATLAB控制平台输入结构分析的各类参数，然后由MATLAB控制参数建模并控制ANSYS软件执行结构的热固耦合分析、模态分析和热分析等，得到与输入参数对应的考核位置的应力、应变、振幅、频率及温度等结构分析结果。疲劳寿命计算部分负责完成MATLAB控制下由输入的结构有限元分析结果进行的各种失效模式下疲劳寿命的计算。疲劳寿命可靠性优化设计部分则主要负责完成优化设计参数的搜索。优化结果部分则输出优化的结果，包括收敛的优化设计方案、寿命均值和失效概率。整个仿真过程中的有限元分析部分为在MATLAB中使用外部文件方法调用ANSYS程序，其余四个部分均在MATLAB内部完成。整个分析过程不需要进入软件界面操作，实现修改参数的自动化。

2 涡轮盘有限元模型、基本随机变量及其结构模型的参数化

本文研究的某型涡轮盘模型如图 2(a)所示，取整体涡轮盘的1/41，即8.78°的扇形对称体来进行有限元分析，如图2(b)所示。本文选取榫槽剖面处9个尺寸{X1,X2,…,X9}以及涡轮盘截面处5个尺寸{X10,X11,…,X14}进行参数化，分别如图3(a)、图 3(b)所示。

(a) 整体模型(a) Whole model (b) 化简模型(b) Simplified model图2 涡轮盘CAD模型Fig.2 CAD model of turbine disk

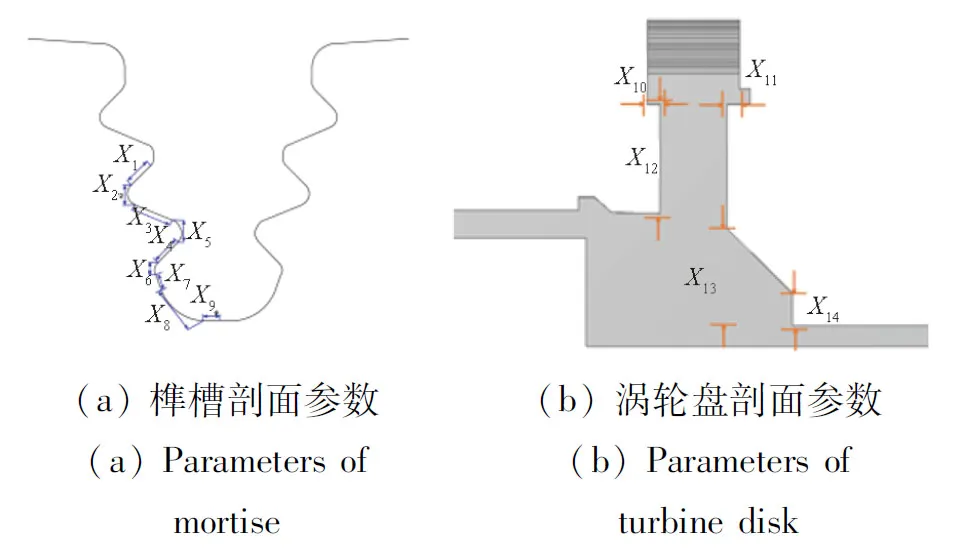
图3 涡轮盘含设计参数的随机变量Fig.3 Random variables of turbine disk including design parameters

涡轮盘疲劳寿命可靠性分析选取7个环境随机变量Z={ω,ρ,αE,αμ,T0,αλ,u}，Z的物理含义、分布形式和参数如表1所示，其中寿命模型分散性辅助变量u将在第4节介绍。涡轮盘的材料为FGH96，材料密度、线膨胀系数、导热率、弹性模量、泊松比参见文献[20-21]。

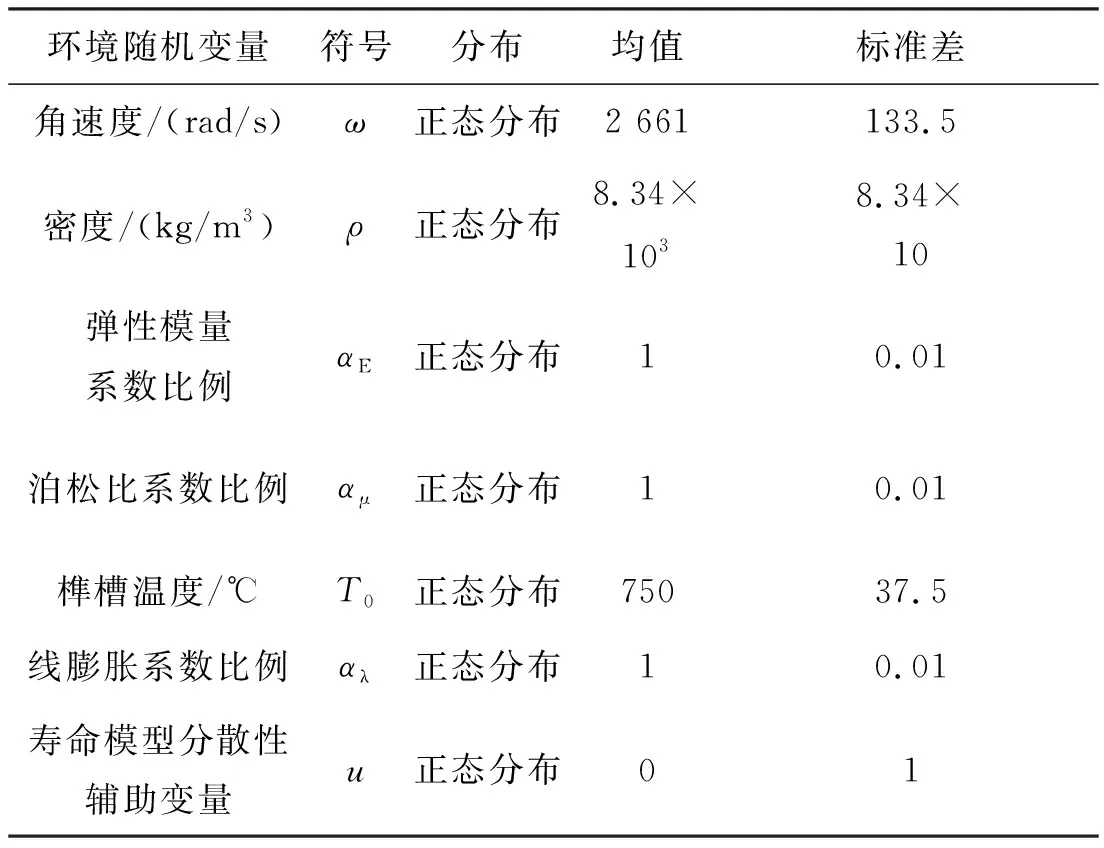
表1 环境随机变量的分布类型与分布参数Tab.1 Distributions and parameters of environmental variables

3 涡轮盘的有限元分析

3.1 热分析

涡轮盘处于高温工况下，温度对于涡轮盘的应力应变有较大影响。盘心处温度较低，设其温度为450 ℃。涡轮盘榫槽与叶片榫头之间有热接触，接触部位的温度为T。涡轮盘热分析获得的温度场计算结果如图4所示。涡轮盘热分析结果将作为边界条件加入热固耦合分析中。

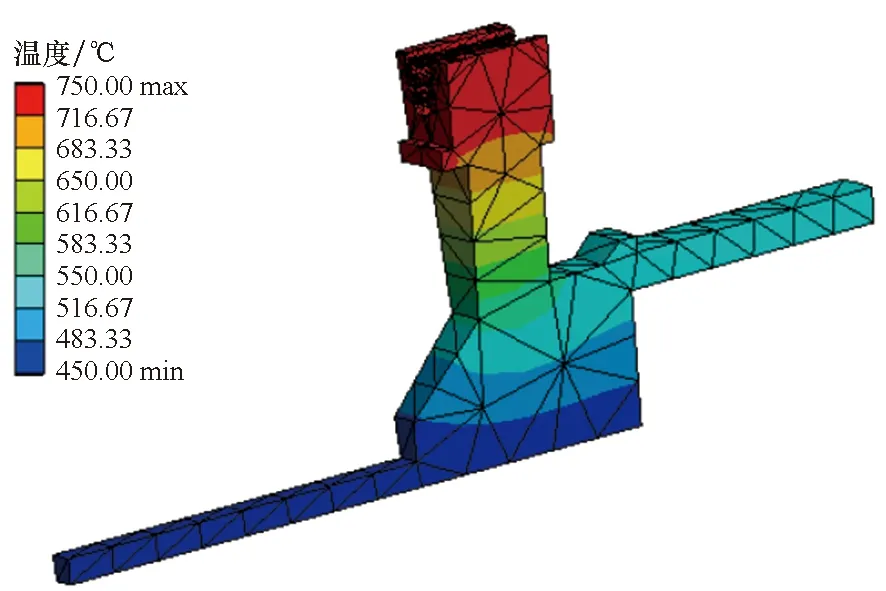
图4 涡轮盘热分析Fig.4 Thermal analysis of turbine disk

3.2 热固耦合分析

涡轮盘所受载荷除上一小节的温度载荷以外，还受到离心力、气动载荷、协调载荷等的作用，本文主要考虑对涡轮盘应力应变影响最大的离心力。使用ANSYS进行热固耦合分析获得榫槽处应力如图5所示，盘心处应力如图6所示。分析涡轮盘的应力分布，发现涡轮盘的危险点有两个，分别位于涡轮盘盘心中部以及榫槽底部，因此后续的疲劳寿命可靠性分析以及可靠性优化设计中均选取涡轮盘盘心以及涡轮盘榫槽两个疲劳寿命考察部位。

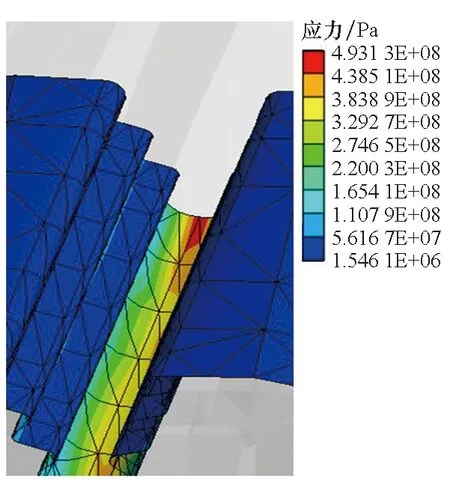
图5 涡轮盘榫槽处应力分布Fig.5 Static analysis of turbine disk mortise

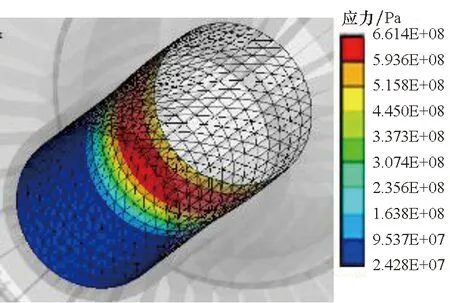
图6 涡轮盘盘心处应力分布Fig.6 Static analysis of turbine disk center

3.3 模态分析

本文取叶片和涡轮盘组成的叶盘系统进行模态分析。叶盘系统所受的激振力为尾流激振力。尾流激振力的频率[22]为k·Nc·ω/6，其中Nc为构造系数，本文以静子叶片数作为构造系数，取Nc=35，ω为叶盘转速，k为谐波阶次。激振力频率与转速关系可以统一写为Fe=K·ω/60，其中K=Nc,2Nc，…。

本文取第一阶激振力为叶片所受离心力的15%[23-24]，在叶尖部位施加横向激励。激振力作用下各随机变量取均值时榫槽危险点处的涡轮盘频率为10 729 Hz，响应为1.81×105Pa，计算获得的涡轮盘频率及响应将用于后续涡轮盘高周疲劳寿命分析。

4 涡轮盘疲劳寿命计算

本文使用如下所示Morrow修正的Manson-Coffin模型[25]计算特定工况下涡轮盘疲劳寿命。

(1)

式中，εa为应变幅值，b为疲劳强度指数，c为疲劳延性指数，为疲劳强度系数，为疲劳延性系数，σm为应力均值，Nf为疲劳寿命。其中、b、c、/E四个参数由低周疲劳实验数据进行异方差回归分析[26-27]获得，如表2所示，标准正态分布u用以衡量材料疲劳寿命分散性的变量，通过引入u可以将低周疲劳寿命模型转换为低周概率疲劳寿命模型。

表2 FGH96材料疲劳寿命模型参数Tab.2 Parameters of fatigue life model (FGH96)

对于多级循环下的寿命估计，本文采用了线性损伤累积法则[25,28-29]

(2)

式中，Di为第i级循环应力导致的损伤，ni为第i级应力水平循环次数，Ni为每种应力水平下对应的由式(2)求得的疲劳寿命。

对于高低周复合疲劳寿命分析，本文使用Corten和Dolan[30]提出的考虑载荷间相互作用的疲劳损伤指数累积模型：

(3)

式中，l为交变载荷总级数，Nf,g为多级交变载荷作用下的疲劳总寿命，Nf,m为多级应力中最大应力作用下的疲劳寿命，αi为各级应力σi作用下的循环数与总循环数的比值，σm为多级交变载荷中的最大应力幅值，γ为材料常数，通常由实验来确定，当缺乏实验数据时，可依据经验公式取近似值。对于FGH96材料，本文取γ=8.081[31]。

5 涡轮盘的疲劳寿命可靠性优化设计

5.1 涡轮盘疲劳寿命可靠性优化模型

以均值寿命最大为目标函数，以寿命可靠性为约束条件，建立了涡轮盘榫槽疲劳寿命可靠性优化模型，模型如下

findd={μx1,μx2,…,μx14}

mb(d)<110

(4)

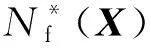
5.2 涡轮盘疲劳寿命可靠性优化模型求解策略

在涡轮盘疲劳寿命可靠性优化设计模型中，寿命函数Nf(X)为含随机变量X的隐函数，且寿命函数与进行寿命可靠性分析的功能函数g(X)有如下关系：

(5)

显然，如果直接采用由有限元分析及寿命分析确定的隐式函数Nf(X)和g(X)进行疲劳寿命可靠性优化设计模型的求解将造成极大的计算量，为此本文基于已有的基于代理模型法的优化求解策略[9,32-33]，建立了涡轮盘疲劳寿命可靠性优化设计模型求解的类序列解耦法。本文所建立的类序列解耦法包括了如下所示两个基本步骤：

第一步是在设计参数和输入变量的扩展空间中自适应构造计算失效概率功能函数g(X)的Kriging代理模型gK(X)，该部分的自适应构建过程中利用的是U学习准则。在第一步训练获得收敛后的gK(X)后，将利用gK(X)由下式来构造寿命函数Nf(X)的初始Kriging代理模型，则

(6)

这种利用gK(X)来构造初始Nf,K(X)的策略可以充分利用已有的训练点来同时得到gK(X)和Nf,K(X)。在得到初始Nf,K(X)之后，需要继续对Nf,K(X)进行自适应训练，以便得到收敛的Nf,K(X)用以计算可靠性优化模型中寿命的均值函数E[Nf(X)]。本文在下一小节中提出一种SVDM学习函数来自适应训练Nf,K(X)，该学习函数可以保证由收敛的Nf,K(X)估计E[Nf(X)]的方差满足预先设定的精度要求值。

第二步则是在第一步构造的Nf,K(X)和gK(X)基础上，完成当前设计参数下代理模型的更新以及基于更新后的代理模型进行可靠性优化设计模型的求解。由于Nf,K(X)和gK(X)将可靠性优化模型中的目标函数和约束函数均显式化，因此可以用序列二次规划法[34](sequential quadratic programming, SQP)等优化方法轻松搜索得到设计参数的优化解。

5.3 构建代理模型gK(X)和Nf,K(X)的学习函数

5.3.1 构建gK(X)的U学习函数

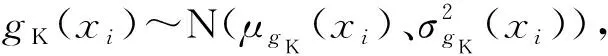
(7)

(8)

minU(xi)>2

(9)

由U学习函数的基本性质可知[15]，当式(9)成立时，表明当前gK(X)可以大于Φ(2)=0.977(其中Φ(·)为标准正态分布函数)的概率正确识别S中样本点状态。本文在构建gK(X)时采用的正是这种U学习函数。

5.3.2 构建Nf,K(X)的SVDM学习函数

在本文所构建的疲劳寿命可靠性优化设计模型中，构建寿命函数Nf(X)的Kriging代理模型Nf,K(X)的目的是为了由收敛的Nf,K(X)代替Nf(X)求解优化模型中的寿命均值，即E[Nf(X)]≈E[Nf,K(X)]。设MCS样本池S尺寸为N，即S={x1,x2,…,xn}，则由Nf,K(X)估计得到的寿命均值为：

(10)

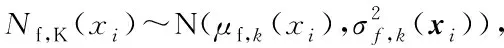
(11)

(12)

其中，Cov(·,·)为协方差算子。

(13)

(14)

(15)

本文所提出的SVDM学习函数在自适应训练寿命函数Nf(X)的代理模型Nf,K(X)时，可以最大限度地降低由Nf,K(X)估计寿命均值的方差，为验证本文所提的SVDM学习函数相对于已有的均方误差(mean squared error, MSE)学习函数[39-41]以及最小最大距离(minimax and maximin distance, MMD)学习函数[42]的优越性，下一小节将给出一个简单算例。

5.4 本文所提SVDM学习函数数值算例验证

一个拥有四个失效域边界串联问题的极限状态方程如式(16)所示[15]，x1、x2均服从标准正态分布且相互独立。

(16)

分别使用SVDM、MMD、MSE三种学习函数训练g(x1,x2)的Kriging代理模型gK(x1,x2)以便由收敛的gK(x1,x2)计算g(x1,x2)的均值E[g]，三种方法的备选样本池均相同，初始训练点集相同且数量为20个，停止准则均为式(15)，获得的结果如表3所示。

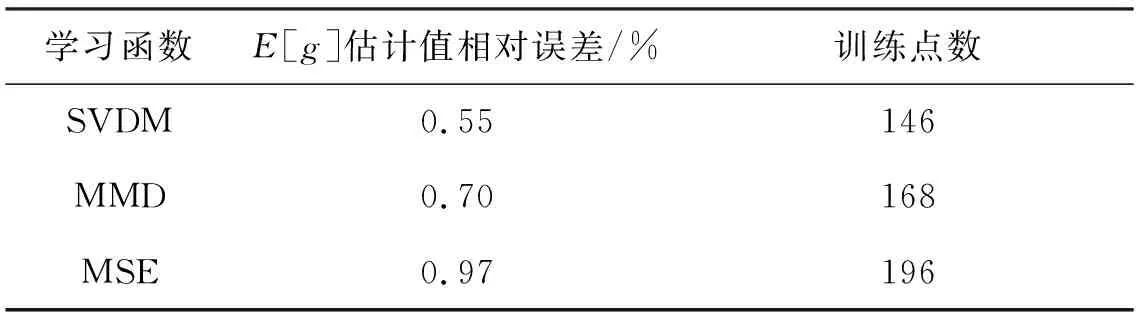
表3 三种学习函数求解悬臂梁优化算例结果比较Tab.3 Comparison of three learning functions for cantilever beam example

通过表3的对比可以看出，相比于MMD和MSE学习函数，在相同初始训练点集下，SVDM学习函数需要的训练点数最少，同时也能获得相对误差最小的均值估计值，这是因为SVDM学习函数总是选择能使E[g]估计值方差减小最多的备选样本点加入训练点集中。

5.5 涡轮盘疲劳寿命可靠性优化设计求解的类序列解耦法流程及步骤

按照5.2小节设计的涡轮盘疲劳可靠性优化设计策略，以及5.3小节给出的构建寿命可靠性分析功能函数和寿命函数代理模型的学习函数，本小节将建立涡轮盘疲劳寿命可靠性优化设计求解的类序列解耦法的流程与步骤，所建立方法的流程如图7所示，主要步骤如下。

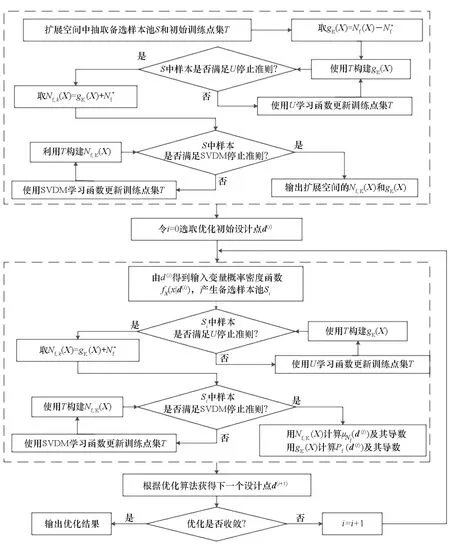
图7 可靠性优化模型求解流程Fig.7 Solution process of reliability optimization model

步骤1：构建包含涡轮盘实际尺寸{X1,X2,…,X14}以及环境变量Z的扩展空间，在该扩展空间中使用Sobol序列抽取所有输入随机变量的备选样本池S以及初始训练点集T。其中，备选样本池S的长度NS需要保证失效概率估计值的变异系数小于5%，即

(17)

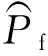
步骤2：使用U学习函数在S中自适应构建涡轮盘疲劳寿命可靠性分析功能函数代理模型gK(X)至收敛。

步骤3：使用训练点集T构建初始gK(X)。

步骤4：依据U学习函数停止准则，即式(9)判别gK(X)的自适应学习过程的收敛性。当满足U学习函数停止准则时，得到收敛的代理模型gK(X)并转入步骤6，否则执行步骤5。

步骤5：在S中依据U学习函数选取训练样本点加入训练点集T中，返回步骤3。

步骤6：使用SVDM学习函数在S中自适应更新代理模型Nf,K(X)至收敛；

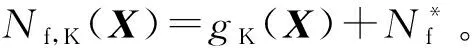
步骤8：依据SVDM学习函数停止准则，即式(15)判别Nf,K(X)的自适应学习过程的收敛性。当满足SVDM学习函数停止准则时，得到收敛的代理模型Nf,K(X)并转入步骤10，否则执行步骤9。

步骤9：在S中依据SVDM学习函数选取训练样本点加入训练点集T中。

步骤10：使用训练点集T构建代理模型Nf,K(X)，返回步骤8。

步骤11：令优化迭代指针i=0并选取优化过程的初始设计参数d(0)。

步骤12：依照当前设计参数d(0)得到输入变量的概率密度函数fX(x|d(i))产生备选样本池Si。

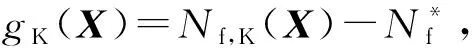
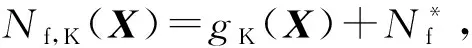
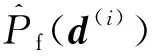
步骤16：利用步骤15的结果和SQP算法搜索得到下一步的设计点d(i+1)。

步骤17：判断SQP算法是否收敛，若未收敛则令i=i+1，返回步骤12。否则输出优化结果d(i+1)，结束优化设计过程。

6 仿真结果

6.1 盘心疲劳寿命可靠性优化

由涡轮盘的热固耦合分析结果可知，涡轮盘盘心的最大应力主要受到离心力影响，而离心力主要与转动速度以及转动惯量有关，因此，涡轮盘盘心优化的主要思路是通过改变涡轮盘形状，降低转动惯量，从而降低盘心最大应力或应变，增加盘心的疲劳寿命可靠性。

涡轮盘盘心疲劳寿命可靠性优化设计选取设计变量d=[uX10,…,uX14]，设计变量的设计域如表4所示，选取正态分布的随机变量X=[X10,…,X14]，其均值为d，标准差为0.1 mm。求解该可靠性优化模型，获得的最优方案与涡轮盘的初始方案比较如表 4和表 5所示。

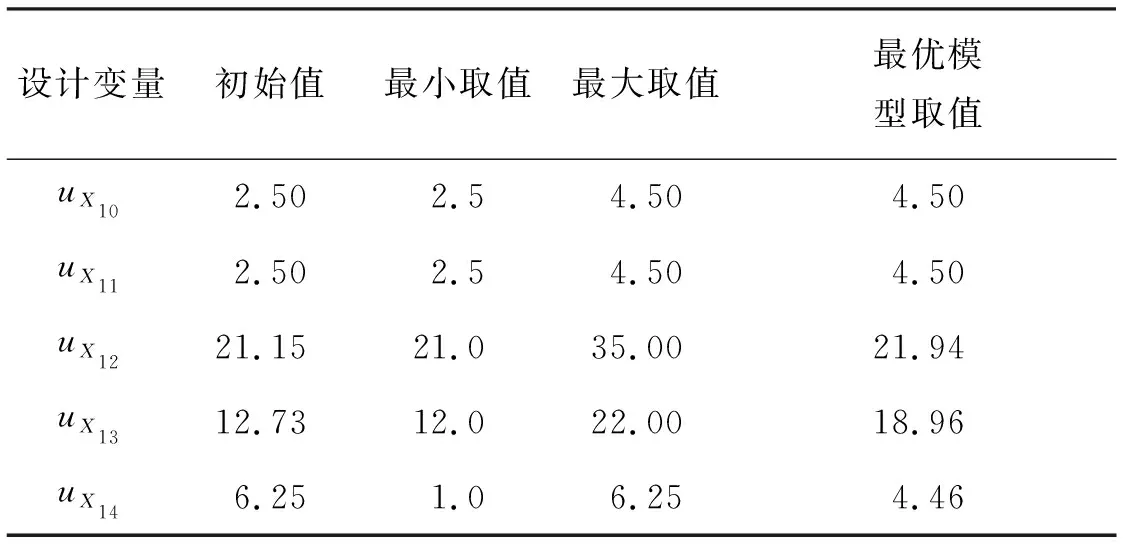
表4 涡轮盘盘心优化设计变量Tab.4 Optimization design parameters of turbine disk center 单位：mm

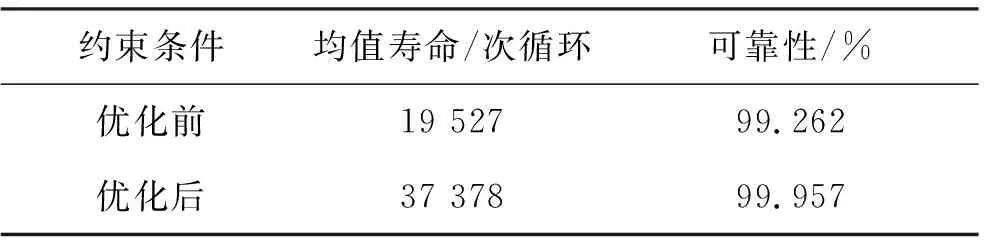
表5 涡轮盘优化前后疲劳寿命可靠性对比Tab.5 Comparison of fatigue life reliability of turbine disk before and after optimization

表6中给出的转动惯量(或质量)测量对象为对称化简后的涡轮盘模型，局部最大应力指的是环境变量取均值且不考虑模型尺寸误差的情况下，有限元分析获得的局部最大应力。由表 5和表 6的结果可知，优化后的模型相比于优化前的模型，转动惯量更小，从而导致离心力减小，局部最大应力减小，疲劳寿命增加。本文在涡轮盘盘心疲劳可靠性优化中，所得优化方案平均降低了约5%的涡轮盘转动惯量与离心力，平均降低了约13%的盘心最大应力，从而使得盘心结构的疲劳寿命均值由19 527次循环提高到37 378次循环，增幅达到91.4%，疲劳寿命可靠度则由优化前的99.262%提高到了优化后的99.957%。

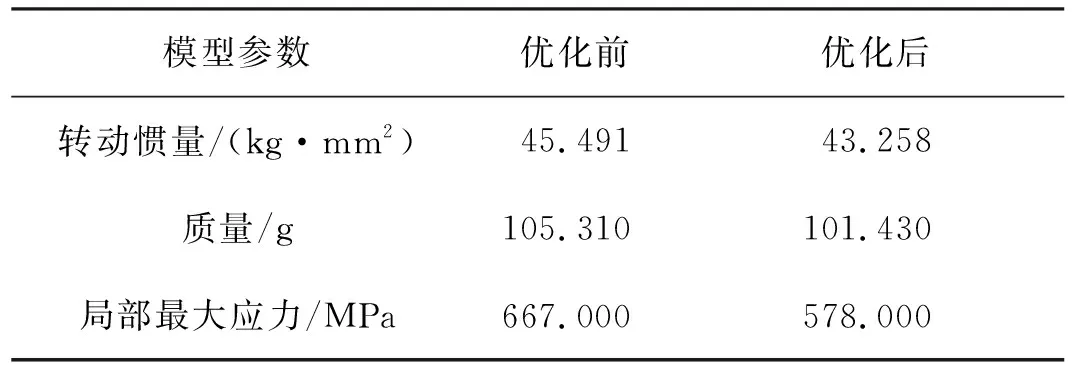
表6 优化前后模型对比Tab.6 Comparison of fatigue life reliability of turbine disk model before and after optimization

6.2 榫槽疲劳寿命可靠性优化设计结果

榫槽存在应力集中现象，榫槽处的最大应力与榫槽的应力集中系数有关。因此，涡轮盘榫槽优化的主要思路是改进榫槽的构型，减小榫槽的应力集中系数，从而降低局部应力应变，增加榫槽的疲劳寿命可靠性。

榫槽的最大应力点位于榫槽开口结构的底部，因此本文在榫槽疲劳寿命可靠性优化设计中选择榫槽底部的三个参数{X7,X8,X9}为正态分布的随机变量，取它们的均值{uX7,uX8,uX9}作为设计变量，并假设标准差为0.1 mm。其余的榫槽剖面参数{X1,…,X6}作为环境随机变量，标准差为0.1 mm。设计变量的取值范围如表7所示。

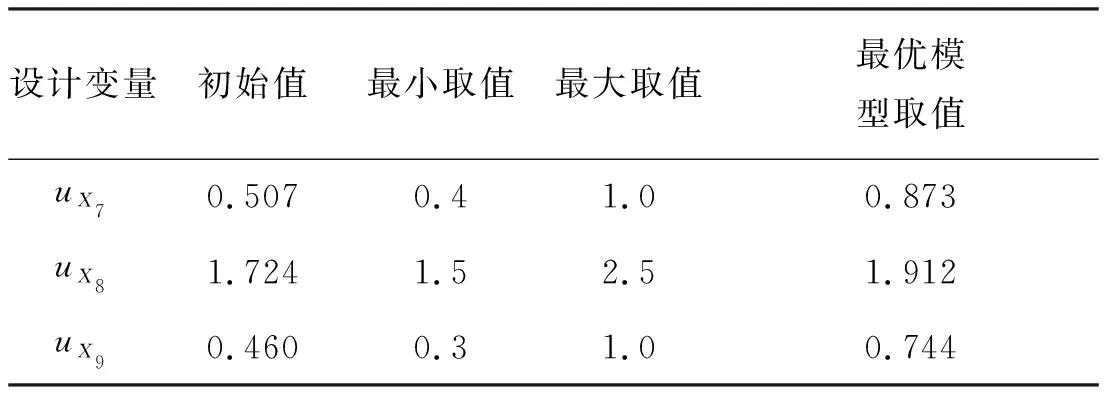
表7 涡轮盘榫槽优化设计变量Tab.7 Optimization design parameters of turbine disk mortise 单位：mm

求解上述模型，获得的最优方案与涡轮盘的初始方案比较如表7和表8所示，优化前后结构分别如图 8(a) 和图 8(b)所示，应力分布如图 9(a) 和图 9(b)所示。

表8 涡轮盘榫槽优化前后疲劳寿命可靠性对比Tab.8 Comparison of fatigue life reliability of turbine disk mortise before and after optimization

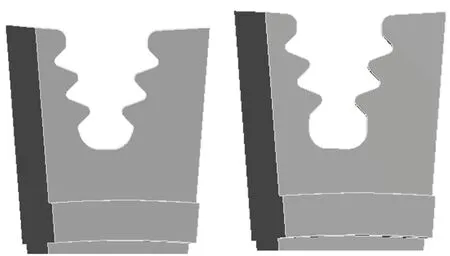
(a) 优化前(a) Before optimization (b) 优化后(b) After optimization图8 榫槽结构Fig.8 Structure of turbine disk mortise

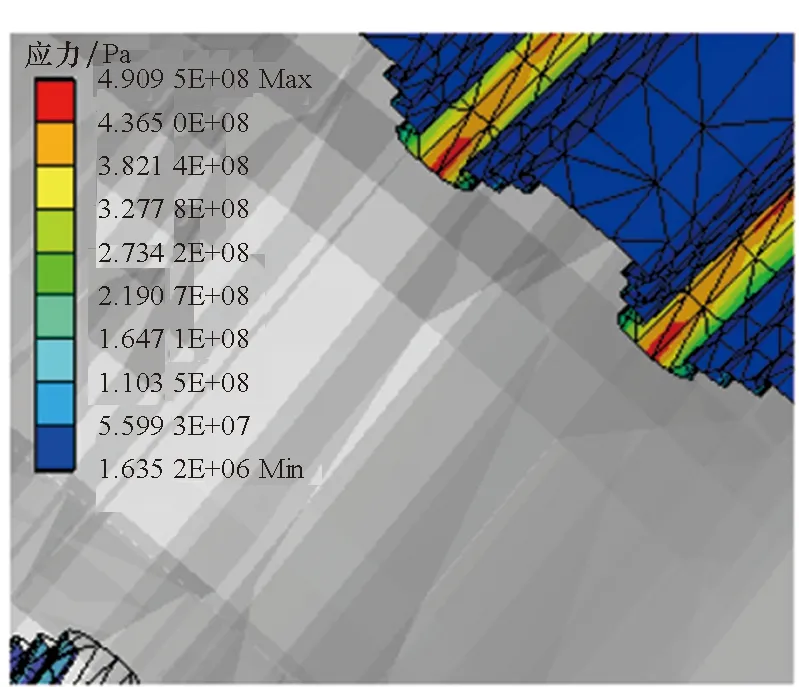
(a) 优化前(a) Before optimization

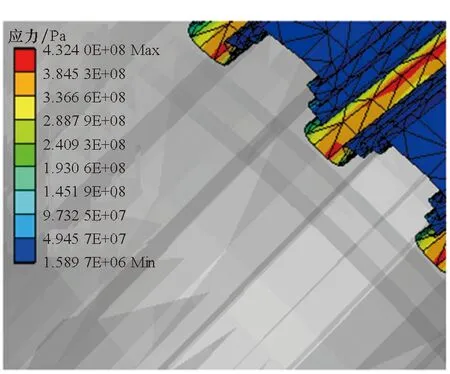
(b) 优化后(b) After optimization图9 榫槽应力分布Fig.9 Stress distribution of turbine disk mortise

由于榫槽存在应力集中现象，榫槽的疲劳寿命主要受榫槽的形状影响。由于优化前榫槽的应力集中部位为榫槽的底部，因此优化的主要过程为调整榫槽的形状，降低应力集中，以减少榫槽的最大局部应变。对比优化前后榫槽的形状，可以看出优化后榫槽底部的开口更为平滑，形状近似圆形，应力集中现象也没有优化前那么突出。本文在涡轮盘榫槽高低周复合疲劳可靠性优化中，所得到的优化方案平均降低了约12%的榫槽最大应力，从而使得涡轮盘榫槽结构的高低周复合疲劳寿命均值由42 824次循环提高到73 047次循环，增幅达到70.6%，可靠度也由优化前的99.413%增加到优化后的99.975%。

6.3 涡轮盘系统疲劳寿命可靠性优化设计结果

本小节将盘心和榫槽构成的涡轮盘系统进行可靠性优化设计，同时考虑涡轮盘盘心和榫槽的疲劳寿命可靠性，即将涡轮盘的盘心与榫槽看作一个串联系统，则涡轮盘的寿命可靠性约束如下

(18)

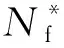
涡轮盘系统疲劳寿命可靠性优化包含设计变量{uX7,…,uX14}。设计变量的取值如表4和表7所示。求解上述模型，获得的最优方案与涡轮盘的初始方案比较如表 9所示。

表9 涡轮盘系统可靠性优化前后疲劳寿命可靠性对比Tab.9 Comparison of fatigue life reliability of turbine disk system before and after optimization

将涡轮盘系统可靠性优化获得的结果分别与盘心、榫槽单模式疲劳寿命可靠性优化对比，如表10和表11所示。由对比结果可以看出：系统可靠性优化获得的结果与单模式疲劳寿命可靠性优化获得的结果的差异很小，由此可以看出榫槽优化与盘心优化互相之间影响很小。涡轮盘盘心优化的主要思路是通过改变涡轮盘形状，降低转动惯量，从而降低盘心最大应力或应变，而改变榫槽剖面尺寸对于涡轮盘离心力影响很小；涡轮盘榫槽优化的主要思路是改进榫槽的局部构型，减小榫槽的应力集中系数，从而降低局部应力应变，而改变涡轮盘剖面尺寸对于榫槽应力集中的影响也很小。通过以上分析，可以认为涡轮盘系统疲劳可靠性优化与盘心、榫槽单模式疲劳寿命可靠性优化获得的结果是一致的。将二者进行对比，盘心、榫槽单模式疲劳寿命可靠性优化精度较高，原因是单模式的优化设计扩展空间中变量数量较少，Kriging模型的精度较高。

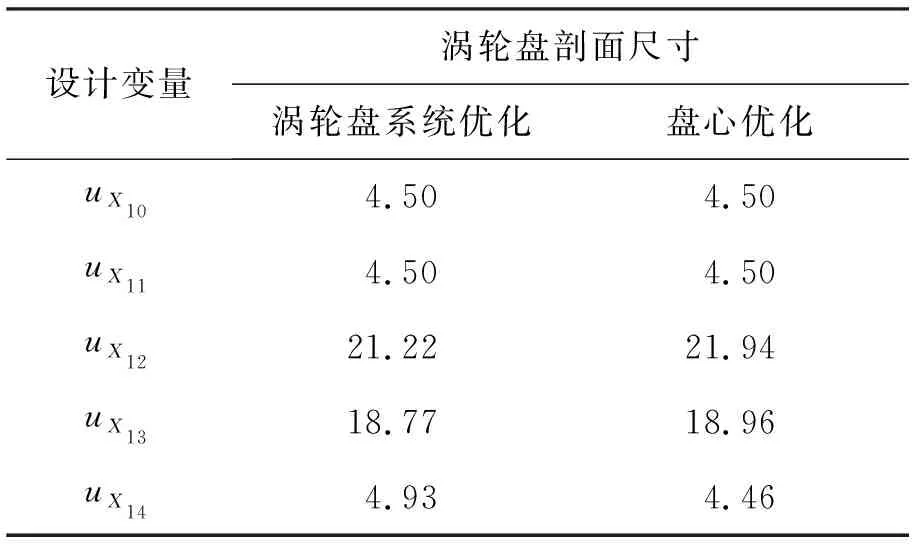
表10 涡轮盘系统可靠性优化与盘心单模式疲劳可靠性优化结果对比Tab.10 Comparison of turbine disk system with turbine disk center for optimization results of fatigue reliability 单位：mm

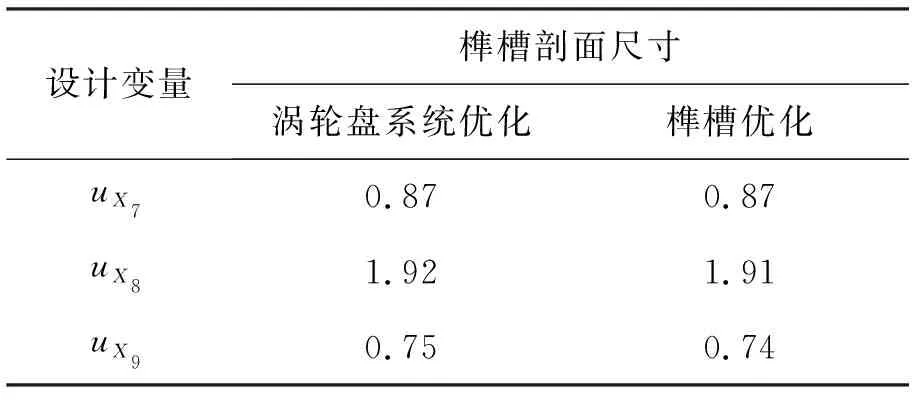
表11 涡轮盘系统可靠性优化与榫槽单模式疲劳可靠性优化结果对比Tab.11 Comparison of turbine disk system with turbine disk mortise for optimization results of fatigue reliability 单位：mm