LWT-FLP去噪算法在FBG传感器信号处理中的应用
2023-03-09河南工业贸易职业学院信息工程学院河南郑州市451191李彩霞
(河南工业贸易职业学院,信息工程学院,河南郑州市,451191)李彩霞
1 引言
在分布式光纤光栅(FBG)传感器检测方法中,最终检测结果的精确程度很大程度上取决于信号处理的精度,在复杂场合这一特征异常显著。测量结果的有效性也有可能受传感网络设计好坏的影响。关于这方面的研究,相关学者深入分析成果显著[1-2]。需要注意的是,前向线性预测(Forward Linear Prediction,FLP)算法以及小波变化常被单独使用在研究过程中[3]。FLP算法的目的为对当前时刻的陀螺信号进行预测,具体计算方法为先前陀螺信号与对应权重相乘。
LWT-FLP算法则综合了前向线性预测算法及提升小波变换的优势,发挥出更高的使用价值。在去噪方面,LWT-FLP算法展现出突出优势,该算法首先要将光纤陀螺信号分层处理,需进行提升小波变化,然后再累积处理高频噪声,在此基础上采用FLP算法对高频系数进行处理,经过此环节后则需完成白化处理[4],重构FBG传感器信号为最后环节的重点,该过程获取的信号在各频域内均已完成去噪处理。对试验结果进行分析发现,FBG传感器输出信号通过此算法可将噪声影响高效去除,这也充分验证在去噪方面,LWT-FLP算法确实发挥最佳作用。
2 LWT-FLP去噪算法
2.1 前向线性预测算法
当前陀螺信号的估计值为:
前向预测误差最小化需以最小均方值理论为依据,为保证代价函数取得最小值权重选择必须适合。将权重迭代公式通过最小均方值理论调整为:
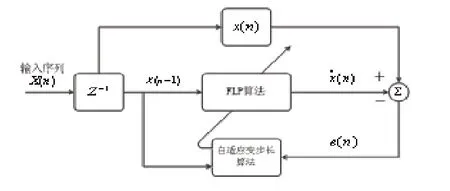
图1 基于自适应的FLP算法结构
2.2 LWT-FLP算法计算流程
LWT-FLP去噪算法作为一种新的高效去噪算法,其充分结合了前向线性预测(FLP)算法以及提升小波变换(LWT)的优势,去噪效果表示更佳。以下为该算法的详细计算步骤:①单支重构各节点的提升小波系数,分解尺度设为N。c(t)、d(t)分别为重构后低频系数和高频系数;②保留低频系数c(t),累加处理高频系数d(t),即采用灰化处理的操作方式来处理由提升小波分解的高频系数;③采用FLP处理上述获取的提升小波高低频系数。对步骤②中描述的灰化后的提升小波高低频系数进行FLP处理。由于预测误差在初始阶段相对较大,为确保能有效降低预测误差数值,步长选择需较为谨慎,该阶段大步长作为最佳选择;稳态输出精度可通过选择小步长得到有效提高,在这之前需确保预测误差降至一定范围内;④采用累减处理经FLP处理的高频系数d(t),同时确保在此之前该系统由提升小波分解获得;⑤提升小波重构。重构N层高低频系数,该系数由步骤④中白化处理获取,加速度计输出信号可通过LWT-FLP算法去噪获得。图2为LWT-FLP算法的结构图。
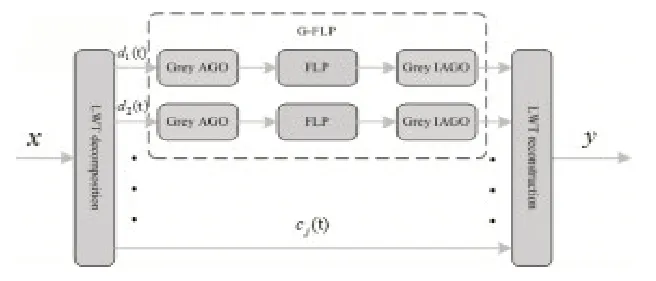
图2 LWT-FLP算法流程图
3 实验结果分析
3.1 信号采集实验方案
FBG加速度数据采集实验是LWT-FLP算法验证首要开展环节。对此需对管壁振动加速度、轴向应变,管道内部流体压力脉动进行逐一测量,数据显示其管子壁厚和管道外径分别为1mm厚、12mm长。充液管在自由状态下的轴向和横向振动特征作为本实验的研究要点。因此按照图3所示的布置图,将测点、相应尺寸的管道以及FBG加速度传感器布置在测试管道上[5]。
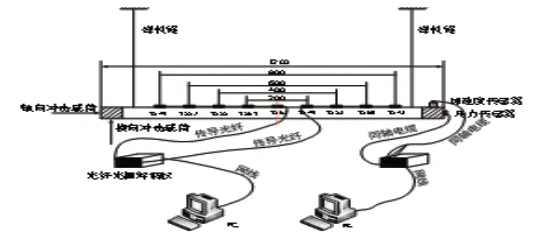
图3 直管试验装置图
用堵头封闭被测试管道的两端,将液压油充入管内,用激振锤来横向和轴向激励管路一端,管道振动加速度信号以及管内流体压力测量设备分别为加速度传感器及压力传感器[6]。
3.2 LWT-FLP去噪算法传感器信号处理结果
在管路一端采取力锤完成横向激励,管道轴向应变和横向振动加速度的检测设备分别为FBG和加速度传感器,力锤敲击信号需随时进行记录,在测量过程共有5次敲击,图4为处理前后加速度和FBG时域波形对比情况。
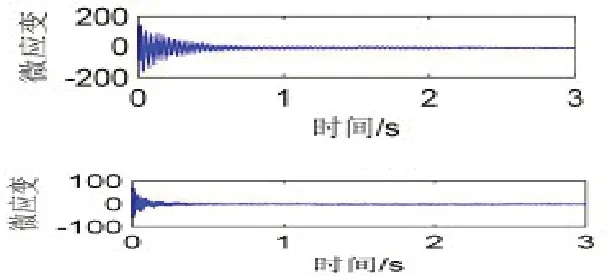
图4 处理前后FBG信号
在对比分析后,发现信号经FBG处理后展现出显著的去噪效果,且与处理前具有相似的变化趋势,这意味着在稳定性和准确性性能方面,FBG传感器可代替标准电磁流量计使用,具有相同功能,因此对照现场使用设计要求,超声波FBG传感器均可满足。
3.3 结果对比
不同算法的去噪效果如图5所示。经对比发现,LWT-FLP算法相比于G-FLP算法及FLP算法这两种传统算法,去噪效果更佳。该结果主要原因是原始数据不平稳特征被消除,加速度计数据则通过提升小波完成多尺度变换;采用灰化处理方式对高频数据进行累加操作,FLP的预测精度得到显著提高,原始数据的规律性更明显。

图5 不同算法去噪效果对比图
计算上述去噪结果的方差和均值,具体数据如表1所示。经对比得出,加速度计输出信号经LWT-FLP算法去噪后,不论是方差还是均值相比原始结果下降幅度都很大,意味着去噪效果十分显著。综上所述,LWT-FLP算法在去噪方面,与GFLP及FLP传统算法相比,确实表现出较强的优越性。

表1 不同算法去噪结果均值和方差对比图
4 结论
为了提高传感器信号处理的精度,提出了一种新的去噪LWT-FLP去噪算法,并在FBG传感器信号处理上应用,信号经FBG处理后展现出显著的去噪效果,且与处理前具有相似的变化趋势,FBG传感器可代替标准电磁流量计使用,具有相同功能。LWT-FLP算法相比于G-FLP算法及FLP算法这两种传统算法,去噪效果更佳。加速度计输出信号经LWT-FLP算法去噪后,不论是方差还是均值相比原始结果下降幅度都很大。
