How to estimate isotope fractionations of a Rayleigh-like but diffusion-limited disequilibrium process?

Zi Xuan Guan · Yun Liu

Abstract The Rayleigh distillation isotope fractionation(RDIF) model is one of the most popular methods used in isotope geochemistry.Numerous isotope signals observed in geologic processes have been interpreted with this model.The RDIF model provides a simple mathematic solution for the reservoir-limited equilibrium isotope fractionation effect.Due to the reservoir effect,tremendously large isotope fractionations will always be produced if the reservoir is close to being depleted.However,in real situations,many prerequisites assumed in the RDIF model are often difficult to meet.For instance,it requires the relocated materials,which are removed step by step from one reservoir to another with different isotope compositions(i.e.,with isotope fractionation),to be isotopically equilibrated with materials in the first reservoir simultaneously.This ‘‘quick equilibrium requirement’ is indeed hard to meet if the first reservoir is sufficiently large or the removal step is fast.The whole first reservoir will often fail to re-attain equilibrium in time before the next removal starts.This problem led the RDIF model to fail to interpret isotope signals of many real situations.Here a diffusion-coupled and Rayleigh-like (i.e.,reservoir-effect included) separation process is chosen to investigate this problem.We find that the final isotope fractionations are controlled by both the diffusion process and the reservoir effects via the disequilibrium separation process.Due to its complexity,we choose to use a numerical simulation method to solve this problem by developing specific computing codes for the working model.According to our simulation results,the classical RDIF model only governs isotope fractionations correctly at the final stages of separation when the reservoir scale (or thickness of the system)is reduced to the order of magnitude of the quotient of the diffusivity and the separation rate.The RDIF model fails in other situations and the isotope fractionations will be diffusion-limited when the reservoir is relatively large,or the separation rate is fast.We find that the effect of internal isotope distribution inhomogeneity caused by diffusion on the Rayleigh-like separation process is significant and cannot be ignored.This method can be applied to study numerous geologic and planetary processes involving diffusion-limited disequilibrium separation processes including partial melting,evaporation,mineral precipitation,core segregation,etc.Importantly,wefindthatfarmoreinformationcanbeextracted through analyzing isotopic signals of such ‘‘disequilibrium’’processes than those of fully equilibrated ones,e.g.,reservoir size and the separation rate.Such information may provide a key to correctly interpreting many isotope signals observed from geochemical and cosmochemical processes.

Keywords Isotope fractionation · Reservoir isotope effect · Rayleigh-like distillation process · Diffusional isotope effect · Numerical modeling · Disequilibrium process

1 Introduction

The isotope fractionations occurred during separation processes often involve the reservoir effect.Importantly,if the size of a reservoir is limited,tremendously significant isotope effects will appear at the end of the separation process.Numerous important geologic and planetary processes are related to such reservoir isotope effects,e.g.,partial melting,evaporation,mineral precipitation,and core segregation.To deal with such isotope effects,the Rayleigh distillation isotope fractionation (RDIF) model has been widely applied to those processes.For instance,the RDIF was used as the theoretical basis for quantitative interpreting isotope fractionations during crystallization and melting processes in igneous rock systems(Morse 2006),determining the natural gas genesis,source rock type,maturity,and calculating the potential gas rate of the source rock (Clayton 1991;Kinnaman et al.2007),studying the evaporation isotope effects in water for obtaining information of the humidity and temperature factors on the surface of the water (Stewart 1975;Bar-Matthews 1996;Worden et al.2007),determining the extent of volatiles loss from samples such as tektites,chondrites,and rock samples from the terrestrial planets(Ritcher et al.2002;Wimpenny et al.2019),etc.

Traditionally,the RDIF model refers to a process of isotope fractionation in an open system,in which the products produced by a reaction or a separation process are in equilibrium with the system (or the first reservoir),and then are removed from the first reservoir immediately after they are formed.The products will be relocated to the second reservoir and isolated,i.e.,they will not be interacting with the first reservoir.After the removal of the products,the RDIF model requires the first reservoir to reach isotopic homogeneity immediately.Therefore,with the repeating of the product-removal process,the isotope composition of the whole first reservoir will be continuously changed.If the size of the first reservoir is limited and when its materials are almost running out,the consequence of such a separation process will be prominent,i.e.,it will always produce extremely large isotopic fractionations in the first reservoir compared to its initial value.

There are three assumptions used in the RDIF model:(1)The two-phase separation is assumed in an equilibrium way;(2)The separation is assumed to be unidirectional,i.e.,there are no backward interactions;(3) The first reservoir is assumed to keep isotopically homogeneous all the time,i.e.,it can re-attain homogeneity or equilibrium in time before the next removal starts.However,these prerequisites,especially the third one,are often difficult to meet in real situations.If the first reservoir is large enough,it will be very difficult for isotope exchange reactions to occur thoroughly for the whole system in time.The third assumption will always fail easily when the systems are silicate melts or solids.Under such circumstances,the non-equilibrium or heterogenous distribution of isotopes within the first reservoir is inevitable.Consequently,the RDIF model will fail to explain the isotope effects,and the actual isotope fraction will be much smaller than the RDIF model’s prediction.

In this study,we try to quantitatively explain those isotope effects involving reservoir effects and disequilibrium separation processes.Under such circumstances,the final isotope fractionation results are caused by the Rayleigh-like repeating separation processes and the internal isotopic heterogeneities are controlled by the diffusion rates of different isotopologues.Previous studies have shown that isotope fractionations can be produced by the diffusion coefficients differences between different isotopes(e.g.,Altabet and Francois 1994;Richter et al.2003;Richter et al.2006;Jones et al.2008;Zhang et al.2010).However,many experimental results suggest that the RDIF will not happen if the diffusion rates in the silicate melts are too slow(Davis et al.1990;Wang et al.1999).We find that only under extreme situations the isotope fractionations can be assigned to the standard RDIF model,but for most cases,the final isotope fractionations are indeed governed by the combined effects of the Rayleigh-like separation process and the diffusion-driven isotope distributions.

2 Methods

In this paper,taking the process of mineral precipitation from a solution or a silicate melt as an example,we consider the phenomenon of isotope fractionation under the influence of both the diffusion effect and the Rayleigh-like separation reservoir effect.Mineral precipitation is a common case of two-phase separation in nature.The crystal and the solution or melt are equilibrated with each other at their interface.Inside the reservoir,from the contact interface to the deep part of the solution the solutes(solved materials) exchange themselves by diffusion.Therefore,the isotope ratio of the removed part (or the precipitate)depends on the isotope ratio at the interface but not the total isotope ratio in solution if the solution part is sufficiently large.

The ‘‘isotopologue’’ refers to molecules that differ only in their isotopic composition,e.g.,H2and HD are two different isotopologues.The difference between two isotopologues’ diffusion rates controls the isotope fractionation between the interface and the deep part of the solution.

We use the classical continuous diffusion equation to describe the thermodynamic phenomena in the studied system and assume that the diffusion of isotopes follows Fick’s law.The function controlling concentration gradients of isotopologues in the liquid or molten phase should be.

whereCis the concentration of each isotopologue,Dis the diffusion coefficient of each isotopologue,μ is the surface flux of each isotopologue,C｜t=0is the concentration at the starting time,are the gradients at the interface and depth of the reservoir.Here it is assumed that the interface is at boundaryx=h.At the boundary,it is assumed that the system meets the standard Rayleigh isotope fractionation conditions,e.g.,the isotope fractionation near the two sides of the interface reaches equilibrium,and the isotope fractionation factor is the apparent fractionation factor(α).If the real-time total flow μ（t）is known,the flow of different isotopologues at the interface can be calculated.

These equations assume that there is only a concentration gradient along thex-axis in the system.This can better approximate the situation encountered in the physical simulation in the laboratory.At the stage of planetary accretion,the system is closer to a 3D or spherical model.In these cases,the differential equation will be slightly different.In particular cases,the differential equation for particular spatial configurations must be established to predict the isotope effect.For the example to be discussed in this paper,it is a reasonable assumption that there is only a concentration gradient along thex-axis in the system,so here only a one-dimensional case is shown.

Assume the fractionation factor at the boundary is α,then there should be

where μAand μBis the flow of each isotopologue;CA（h）andCB（h）is the concentration of each isotopologue at boundaryx=h.Thus,the boundary conditions of both isotopologues depend on total surface flux and the fractionation factor α:

where μtis the total surface flux at timet.Together with the initial conditions,the equations above(Eqs.1,2 and 3)fully describe the behavior of different isotopologues in the RDIF model.These equations are independent of different isotopologues,so they can also be used to describe the distribution of different trace elements.By assuminghis infinite,Eq.(3) can be transformed and deduced out an analytic or exact solution (Wang et al.1999).Under such an assumption,the isotope composition of the materials in the deep reservoir will keep constant,but the isotope compositions close to the interface will be continuously changing and depend on the ratio of the diffusion rate and the separation rate.Especially,the materials close to the surface will have a constant gradient of isotope composition.In this study,we further investigate the cases whenhis not infinite.Since the boundary conditionx=his continuously changing in the process,it is not easy to solve these equations analytically.We have to solve them by using a numerical simulation method.

2.1 Numerical experiments

Figure 1 shows the schematic diagram of the simulated process.For ease of calculation and comparison,it is assumed that α is a fixed and known factor.Note that this coefficient may be a function of temperature,pressure,and composition of the solution in real situations.If all the conditions are known,our calculation method can also handle the case where α constantly changes during the fractionation.In this section,α is treated,or assumed,as a constant that does not change during the fractionation,so it will be easier to discuss how different parameters affect the diffusion.

Transforming the original differential equations to difference equations,wherexis theX-axis coordinate,tis time,Cis the concentration of each isotopologue andDis the diffusion coefficient:

whereC（x，t+Δt）depends onC（x，t-Δt）,C（x，t）andC（x，t+Δt）,for nodes that are not on boundary.

Assuming the initial condition to be

then the boundary condition onx=0 is

which means

Thus,C（0，t）depends onC（Δx，t）.

For boundary condition onx=h（t）=L-vt,

which means

where μ（t）is the surface flux of each isotopologue,Lis the initial thickness,C（L-vt，t）depends onC（L-vt-Δx，t）and μ（t）.

For simplicity of calculation,we simply assume the boundary of this system always moves with a constant speedv.Then,

For isotopologueAandB,

In conclusion,with this numerical method,we can calculate the concentration of isotopologues iteratively.For each Δt,the concentration in the center depends on the concentration at the last Δt.The concentration at the boundary depends on both the adjacent concentration and the flux μt.

With the removal of a node at boundary,its matter is added to the new boundary node.There would be small numerical errors as the boundaryh（t）=L-vtmoves in this way(Fig.1).We use a small time-step and an average concentration on determining μtto minimize the error.

Fig.1 Schematic diagram of the simulated process.The first reservoir is the solution or the melt with solutes in it and as shown as the‘Remaining Matter’’.The precipitated mineral is the second reservoir and as shown as the ‘‘Empty/Never Return’’.The orange cycles are‘nodes’’or‘‘micro-elements’’to represent a very small amount of materials at certain positions.From the left to the right,the decrease of nodes represents the process that materials are removed from the first reservoir continuously until it is almost running out.μ is the surface flux of each isotopologue and it relates to the isotope fractionation occurred at boundary place(x= h).The flux is zero for all isotopologues at the boundary place at the bottom side.Whenever time Δt passes,the most inner nodes inside of solution are first calculated.Then other inner nodes are calculated.Then the real-time μ is calculated.After that,the boundary nodes are calculated.If the boundary moves,the matter of the boundary node is added to the new boundary node,which would cause some errors (Inherited Errors)

During the simulation,the variation of the isotope concentration between adjacent micro-elements (or nodes)may be small when the time and space are differentiated.In practice,the diffusion coefficient and fractionation factor are usually pretty small,and the difference value of the concentration may exceed the precision limit of floats and doubles.Therefore,we have adopted high-precision numbers (Multiple Precision Floating-Point,MPFR) for all floats,which minimizes the systematic error caused by insufficient calculation precision at the cost of computational multiplication.

3 Results

In order to investigate the effect of each parameter on isotope fractionation,the following conditions as the basis for comparison are set: a 100 cm long transversely homogeneous melt,which was converted to another phase in an approximatively Rayleigh-like fractionation condition in 50,000 years.The initial ratio of the two isotopologues considered is 5:100,and the fractionation factor (α)at the interface is 1.05.The diffusion coefficient of the two isotopologues in the melt is close to about 1.0 cm2/year(3.17×10-12m2/s),which approximates the diffusion coefficient of a species in a molten silicate.Other environmental factors,such as ambient pressure,temperature,and composition of other substances in the melt,are ignored in the calculations.These factors may affect the absolute isotope fractionation factor,the rate of phase change,or the rate of diffusion.The discussion excludes the complicated influencing factors behind the variables to simplify the model and uses a control variable method to discuss the impact of these variables on the fractionation process.

Given these conditions,we can simulate the change in the isotope ratio at different locations in the melt over time by calculating the isotope ratio at each time at each point.This simulation provides a set of curves representing the real-time spatial distribution of isotope ratios.These curves are compared to the theoretical curve of the standard RDIF model to verify how variables may affect RDIF.

3.1 The effect of diffusion coefficients on isotope fractionation

As shown in Fig.2,the diffusivity has a significant impact on the fractionation result,when the chemical equilibrium inside the remaining matter(or the first reservoir)cannot be reached by diffusion.Blue lines are the spatial distributions of isotope composition based on our calculation along the length of the remaining matter.Following the separation process,the remaining reservoir becomes smaller and smaller and the blue lines become shorter and shorter.The purple dashed lines are invariant and show the results of the RDIF model.The red ‘‘+’’ character is the mean isotope composition value of the remaining reservoir based on our numerical simulation.The green line is the regression line fitting those red mean values.With the increase of diffusion rates(i.e.,from left-top to right-bottom of Fig.2),the results will eventually approach the curve of RDIF model.

If we define a critical valueDcrit=L·v,whereLis the length of remaining matter,vis the separation rate.When the diffusion coefficient is two orders of magnitude smaller thanDcrit,the remaining matter’s internal isotope ratio is almost no longer affected by the external fractionation occurring at the boundary (Fig.2,left-top inlet).

Fig.2 Spatial distribution of isotope ratios (RBA=CB/CA) over time.In Figs.2,3,4,5 and 6,the horizontal coordinates are the Length (or thickness)of the system,and the vertical coordinates are isotope ratios.Diffusion rate is 0.01 cm2/year(left-top);Diffusion rate is 0.10 cm2/year(right-top);Diffusion rate is 0.20 cm2/year(left-bottom);Diffusion rate is 1.00 cm2/year(right-bottom).The blue lines are the spatial distribution of isotope ratios for different separation stages.The red dashed line with markers is the mean isotope ratio of each stage.The green dashed line is the regression line for Rayleigh-like fractionation,and the purple dashed line is the ideal Rayleigh fractionation line

When the diffusion coefficient is approximately the same order asDcrit,diffusion,and Rayleigh fractionation work together on the isotope fractionation result.WhenDcritis much smaller than the diffusion coefficientD,the interior of the system is always approximately equilibrium.Only at that time,the system can be approximately treated as the ideal RDIF model.

3.2 The effect of length on isotope fractionation

The size of the reservoir is described by a single length(or thickness) variable.With all the other variables held constant,the length variable is changed from 100-5000.The deviation of the simulated results from the ideal RDIF model gradually increases as the length increases (Fig.3).

Fig.3 Spatial distribution of isotope ratios over time with fixed separation rate (1 cm/500 year).Length 100 cm (left-top);Length 500 cm(default) (right-top);Length 2000 cm (left-bottom);Length 5000 cm (right-bottom).The blue lines are the spatial distribution of isotope ratios for different separation stages.The red dashed line with markers is the mean isotope ratio of each stage.The green dashed line is the regression line for Rayleigh-like fractionation,and the purple dashed line is the ideal Rayleigh fractionation line

3.3 The effect of separation rate on isotope fractionation

As shown in Fig.4,as the separation rate is greatly increased,the entire fractionation process is much closer to a stripping process than a conventional Rayleigh fractionation process.In the initial stage of the whole process,the isotope ratio distribution outside the remaining matter is a fixed shape.The average isotope ratio of the residue decreases approximately linearly with the decrease of the remaining matter.

Fig.4 Spatial distribution of isotope ratios over time,with different separation rate.Separation rate 1 cm/4 year(left-top);Separation rate 1 cm/20 year (right-top);Separation rate 1 cm/100 year (left-bottom);Separation rate 1 cm/500 year (right-bottom).The blue lines are the spatial distribution of isotope ratios for different separation stages.The red dashed line with markers is the mean isotope ratio of each stage.The green dashed line is the regression line for Rayleigh-like fractionation,and the purple dashed line is the ideal Rayleigh fractionation line

3.4 The effect of fractionation factor on isotope fractionation

On the other hand,as shown in Fig.5,the fractionation factor does not significantly influence the deviation of the simulated results from the ideal RDIF model.

The diffusion coefficient,thickness,and separation rate determined the relative proportion of the diffusion effect and the Rayleigh fractionation effect on the isotope ratio.For isotope fractionation factors in this range:0.8＜α＜1.2,the calculation shows thatmeansD＜0.1Lv,whereDis the diffusion coefficient;Lis the thickness;vis the rate at which the thickness decreases with time.Under this situation,the effect of diffusion will become quite significant.And,withwhich meansD＜0.5Lv,the effect of diffusion will start to be observed.

3.5 On diffusivity differences of isotopes

Richer et al.(2003)summarized the diffusivity differences of isotopes as follows,where β is a parameter to be determined from the experimental data.The reported max value of β is for the lithium isotope system:βLi=0.215.Assuming that=1.0337,our calculations show isotopes’ diffusivity difference has little impact on these Rayleigh-like fractionations with a max simulated Δαregressed＜0.00001 (Fig.5).

3.6 Elemental partition

This model can also be used to simulate elemental partitioning.In Fig.6,we use the logarithm of concentration as theY-axis to show the simulation experiment’s concentration result.The distribution of elements in a Rayleighlike but disequilibrium process exhibits similar behavior to those of isotope fractionation cases.In addition,diffusion effects can influence elemental partition more significantly than isotope fractionation.This finding agrees with the important issue raised by element partition results of many previous studies on disequilibrium partial melting processes (e.g.,Qin 1992;Van Orman et al.2002;Liang et al.2013;Liang and Liu 2016).Similarly,significant disequilibrium melting results will occur when the chemical exchange between a residual mineral and partial melt is too slow compared to the rate of melting.

4 Discussion

To test this model,we have studied several specific cases.

4.1 Volatile loss

The isotope fractionation signals during evaporation can be used to estimate the extent of the loss of volatiles.The RDIF model is often used in this estimation.There are many examples showing that the observed isotope fractionation results mismatched the theoretical estimation based on the Hertz-Knudsen equation (Richter et al.2002;Richter 2004;Richter et al.2007) and the RDIF model.People have suggested that those discrepancies are caused by several reasons including the saturated vapor pressure,vapor species,and disequilibrium process,etc.Here,the disequilibrium situation will be tested.

Wimpenny et al.(2019) presented the results of Zn isotope analyses about experimentally heated soil samples.They heated soil samples as well as those environmentally derived fallout melt glasses,and australite tektites to deepen the understanding of the kinetic effects of zinc isotope fractionations during thermal-driven evaporation.

The analysis of the major and trace elements of molten glasses produced during the heating of rhyolitic and arkosic soils shows that isotope fractionation becomes more and more significant as temperature and time increase.They assumed that the initial zinc isotope ratio in rhyolitic and arkosic soils was similar to the upper continental crust(UCC) value.The experimental results and the RDIF model are used to obtain an isotope fractionation factor(α)of 0.99879 ± 13.This factor is significantly different from the theoretically predicted value (i.e.,0.985) based on the Hertz-Knudsen equation(Richter et al.2002;Richter 2004;Richter et al.2007).

We bring the conditions like those of the experiment of Wimpenny et al.(2019) into our simulation model,assuming that the temperature factor in the experiment uniquely determines the diffusion coefficient and the separation rate,and using the enrichment factor to estimate the evaporation factor.These simplifications and approximations will affect the reliability of the final results to a certain extent.Rooting Wimpenny et al.‘s work,all samples’ evaporation time was not exceeding 120s,while the enrichment factor was possible below -90.Based on the work of Baker and Watson(1988)and Koepke and Behrens(2001),Wimpenny et al.(2019) estimated Zn diffusivities of 3×10-6cm2/s at 1600 °C and 2×10-5cm2/s at 2000 °C.

For various samples at various temperatures in the experiment,different simulation conditions are used for numerical simulation.The fitting results show that the disequilibrium separation process itself could cause the experimental results.Figure 7 shows the results of Rhyolite soil heated to about 2200 °C as an example.The pattern of such spatial isotope distribution is related to the cases with small diffusion rate (e.g.,Fig.2.left-top inlet) or fast separation rate (e.g.,Fig.4.left-top inlet).The simulation conditions in this fitting are a diffusion coefficient of about 2×10-6cm2/s,a total evaporation time of about 240 s,and a sample diameter of about 3 mm.In this fitting,the diffusion coefficient is slightly less than the estimated value of Wimpenny et al.(2019).Under such conditions,the isotope fractionation occurring at the boundary place will not have a visible effect on the inner isotope ratio during an extensive range of separation stages(as shown in Figs.2,3 and 4).Correspondingly,the isotopic composition of the whole remaining system changes almost linearly before half of the evaporation process.It can be seen clearly that such experimental results are not appropriate to be interpreted by the RDIF model.

4.2 CAI-like liquid evaporation

Experiments on molten Type-B CAIs exposed to high vacuum suggested that the enrichment of heavy isotopes of magnesium in the residue exhibited a Rayleigh distillation fractionation curve (Richter et al.2002).However,the experimentally fitted fractionation factor does not meet the theoretical expectations based on the Hertz-Knudsen equation.The best-fit fractionation factor is much smaller than the theoretically expected value.It is also in line with our numerical simulation of the diffusion-driven and Rayleigh-like disequilibrium separation processes.

Fig.7 Comparison between our calculation results and experimental data (Wimpenny 2019).The blue lines are the spatial distribution of isotope ratios for different separation stages.The red dashed line with markers is the mean isotope ratio of each stage.The green dashed line is the regression line for Rayleigh-like fractionation.Red diamond is experimental data from Wimpenny et al.For simulated data,evaporation factor is ratio of residual substances to total substances.For experimental data,evaporation factor is determined by enrichment factor

Based on experimental conditions,Richter et al.(2002)built a model based on the Hertz-Knudsen equation to simulate the experimental results.Their model includes the relationship between saturated vapor pressure and temperature,oxygen fugacity and melt composition.It also considers the diffusion effect in the melt and the evaporation rate affected by the surrounding gas.They believe that if the magnesium isotope anomaly in the TYPE-B CAIs comes from a thermal process and the original Mg isotope composition in the solar system is about even,then this should mean that the loss of Mg in the process may be between 0 and 50%.

We bring the experiment of Richter et al.(2002)into the model described in this article and recalculate their simulation.As mentioned above,only the assumption of the condensed phase being in the one-dimensional direction is considered in the model.At the same time,only the behavior of the Mg isotopes in the system is considered.Also,the rate of evaporation is assumed to be constant.These simplifications are used to make it easier for people to understand the isotope fractionation produced by this model.The results of our model are compared with the actual experimental results provided by Richter et al.(2002).Our calculations meet almost the same shape as the curve of experimental data (Fig.8).

Under the conditions of time and thickness in the experiment,when the diffusion coefficient is 6×10-12m2/s,the simulation can obtain an apparent fractionation factor,which matches the experimental result.As shown in Fig.8,the influence of the diffusion effect is quite pronounced under this experimental condition.When the total evaporation of magnesium is low,the fractional distillation at the boundary will not affect the internal isotope ratio.The isotope ratio near the boundary takes on a fixed shape and moves inward as magnesium evaporates.Therefore,the initial isotope fractionation value has a linear relationship with the evaporation of magnesium.As the residual magnesium decreased,the fractional distillation at the boundary began to affect the internal isotope content.At this time,the Rayleigh fractionation effect began to take effect.Therefore,considering only the overall isotope ratio and fitting with the Rayleigh model,the best fitting fractionation factor closer to 1 than the actual boundary fractionation factor will be obtained.

Fig.8 Comparison between our calculation results and experimental data (Richter 2002).The left is the calculation results with D=6×10-12m2/s.The red dashed line with markers is the mean isotope ratio of each stage.The green dashed line is the regression line for Rayleigh-like fractionation,and the purple dashed line is the ideal Rayleigh fractionation line.The right is the experimental data from Richter et al.It’s said that FMg=0.5δ25Mg+0.25δ26Mg.The purple dashed line is the ideal Rayleigh fractionation line with

4.3 Crystallization of magma

This model can also be used to simulate the crystallization process of magma.Maner IV et al.(2019) used the RDIF model to analyze the garnet crystal composition in granite igneous rocks.Previous studies have shown that as the crystallization process progresses,the ratio of iron to manganese in garnets decreases,and the manganese content in garnets increases (Cerny et al.1985).The garnet’s Mn content gradually increases from biotite granite to pegmatite,garnet muscovite granite (Miller and Stoddard 1981).However,experiments on the crystallization of garnet from silicon melt have shown that manganese is more compatible with garnet than iron at moderate pressure and temperature (650-750 °C,200 MPa) (Icenhower and London 1995).Maner IV et al.believed that manganese’s compatibility in other mafic phases(biotite,cordierite,and tourmaline) was lower than that of iron,and the Rayleigh fractionation’s effect had controlled the fractionation mode of garnet in granitic igneous rocks.Thus,it can explain the emergence of spessartine-rich garnets in the last stage of granite magmatism.

However,various elements diffuse slowly in the melt at moderate temperatures.According to the data from Zhang et al.(2010),the diffusion coefficient in silicon melt satisfies ln(D)=ln(D0)-E/RT,whereDis diffusivity,D0is the preexponential factor,E is the activation energy,R is the gas constant,and T is the absolute temperature.At moderate temperatures (650～750 °C or about 1000 K),the diffusion coefficients of Mg,Fe,and Mn are about ln(D)=-35～-40.We imitated the conditions of Maner IV et al.and simulated the change of MnO/FeO in the melt according to the distance between crystals (based on the backscattered electron image (BSEI)) and the partition coefficient measured by their experiment.As in Fig.9,it

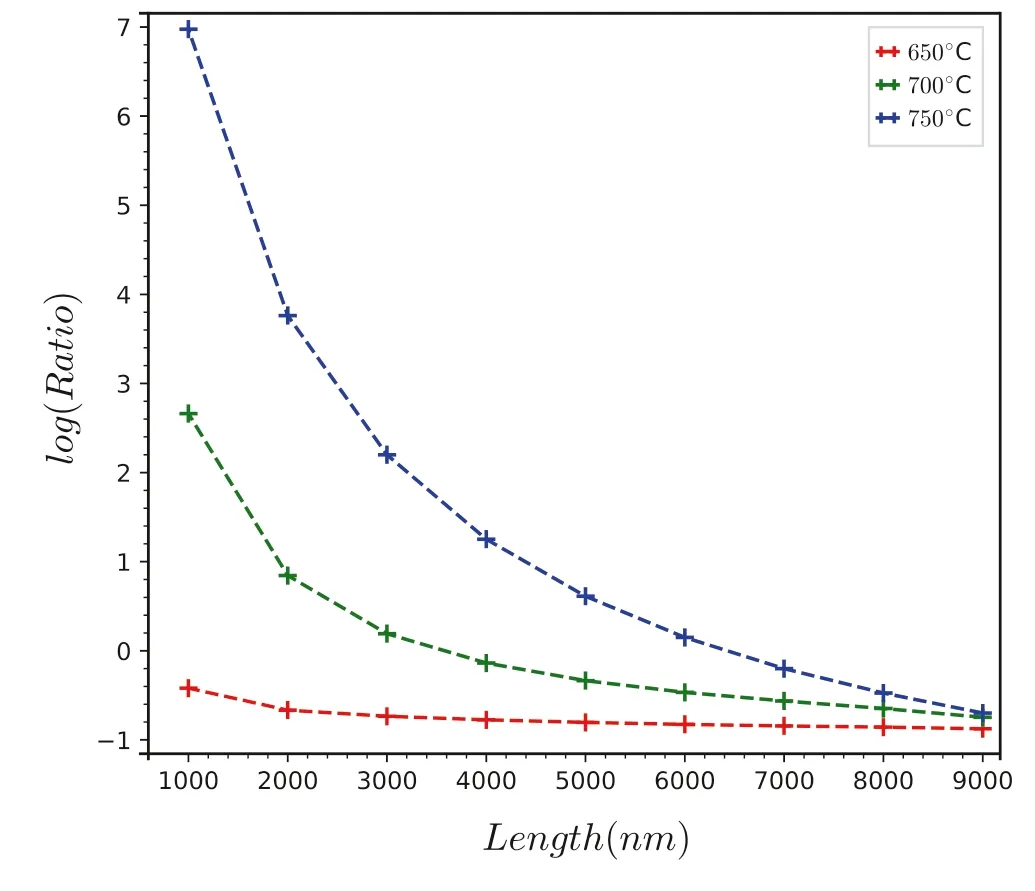
Fig.9 Simulation for a disequilibrium process of the MnO/FeO ratios of melt resulting from a Rayleigh-like crystallization of tourmaline.The red dashed line with markers is the mean Mn/Fe ratio in the melt of each stage at 650 °C.The green dashed line with markers is the mean Mn/Fe ratio in the melt of each stage at 700 °C.The blue dashed line with markers is the mean Mn/Fe ratio in the melt of each stage at 750 °C.The crystallization of tourmaline is the most effective driver of the melt composition to the high MnO/FeO ratios and MnO content that would foster the crystallization of spessartine(Maner IV et al.2019)

4.4 D/H ratio of Mars

It has long been observed that the D/H ratio of the Martian atmosphere and meteorites is much higher than that of the Earth’s oceans (Kurokawa et al.2014;Villanueva et al.2015).This observation may be due to a process similar to Rayleigh fractionation caused by water loss from the surface of Mars.However,modern observations also show that the hydrogen isotope distribution on Mars is not uniform.Some basins and terrain depressions show relatively higher enrichment,while the enrichment of high-altitude areas is relatively low.(Villanueva et al.2015).Therefore,both the diffusion effect and the Rayleigh fractionation process are likely to play an essential role in the loss of water on Mars.The modern observed Mars D/H,based on the results of our numerical simulation experiments,is likely only to indicate the Rayleigh process in the final stage of water loss.These data are difficult to estimate the amount of water on Mars in the past.This means that the water that was once on Mars may have been much more than people expected today.

4.5 Evaporation experiments of synthetic forsterite

Davis et al.(1990) conducted the evaporation experiment of synthetic forsterites (Mg2SiO4).The experimental results show that almost no isotopic fractionation occurs by evaporation in the solid state (1750 °C).The isotope fractionations of O,Mg,and Si in the liquid state(＞1900 °C)are slightly smaller than the results calculated by the theory based on the Hertz-Knudsen equation.It is thought that the influence may be caused by the diffusional effects.Wang et al.(1999) conducted a solid-state simulation experiment in the temperature range of 1500-1800 °C and measured the near-surface gradient of isotope ratio.Based on their derived semi-infinite model,the diffusion coefficient of Mg in the solid state and the corresponding isotope fractionation factor at the interface were deduced.The evaporative isotope fractionation factor obtained by the semi-infinite model fitting is smaller than that obtained by Davis et al.(1990) using the classical Rayleigh distillation fractionation model.

Using the model suggested in this paper and bringing in the experimental conditions used in Davis et al.the time and space scale of the experiment and the isotope fractionations obtained from the experiment,and also assumed that at the surface the Mg isotope fractionation factor is close to the theoretical Mg isotope fractionation factor α=,it can be deduced that the diffusion coefficients of Mg in liquid under experimental conditions are 2.4×10-9m2/s at 1900 °C and 8.0×10-9m2/s at 2050 °C.

According to previous experiments,the diffusion coefficient of Mg element varies greatly in different systems.At the same temperature,the diffusion coefficient between the fastest diffusing andesite system and the slowest diffusing Na2O-CaO-Al2O3-SiO2system can differ by about three orders of magnitude (Zhang et al.2010).The fitting Mg diffusion coefficient results at 1900 and 2050 °C [i.e.,ln(D)=-19.8,ln(D)=-18.6] are consistent with those extrapolated ones based on olivine dissolution experiments[i.e.,ln(D)=-19.99 ± 1.88,ln(D)=-19.21 ± 1.84](Zhang et al.2010;Chen and Zhang,2008).It shows the results of our model are reasonable.

5 Conclusion

The influence of internal heterogeneity caused by diffusion on the Rayleigh-like separation fractionation must be considered.Regardless of the scale of the system and whether the effect of diffusion can be ignored,Rayleighlike fractionation always occurs,unlessD≫L·v.It is proved that bringing the ideal interfacial fractionation factor (α) to the results of this Rayleigh-like fractionation does not yield the correct reaction factor.Also,the regression fitting of isotope ratios at different stages did not yield correct interfacial fractionation factors.

According to the calculations in this study,the RDIF model may fail in predicting the bulk isotope ratio during the earlier stages.The dominating effect can be diffusion when the system has a relatively large scale,a fast separation rate,and a low diffusivity.In these systems,the standard RDIF model cannot give good approximate and will give a relatively small interface isotope fractionation factor.In the late stages,however,with the reduction of the system’s scale,the isotopic behavior will be more like the standard RDIF model.

Also,the fitted apparent fractionation factor is affected by the diffusivity,separation speed,system thickness,and ideal interfacial fractionation factor.The larger the diffusivity,the slower the separation speed,and the smaller the system thickness,the closer the apparent fitting fractionation factor is to the ideal interfacial fractionation factor.Otherwise,the fitted α will be closer to 1.0.It means that the theoretical isotope fractionation factors based on the theory of Hertz-Knudsen (e.g.,Richter et al.2002) cannot be used for such situations.Even if the diffusion rate is slightly less than the one that can meet the perfect Rayleigh distillation model,the isotope fractionation factor will be significantly different from the one based on the Hertz-Knudsen equation.On the other hand,the α obtained by regression can be used to estimate the degree of deviation from the Rayleigh fractionation model.

AcknowledgementsThis work is supported by the Strategic Priority Research Program (B) of CAS (No.XDB41000000),Pre-research Project on Civil Aerospace Technologies No.D020202 funded by the Chinese National Space Administration (CNSA) and Chinese NSF projects (No.42130114) and we thank Yi-Ning Zhang for helpful discussions.

Declarations

Conflict of interestOn behalf of all authors,the corresponding author states that there is no conflict of interest.