考虑乘客风险等级的网约车拼车调度优化模型
2023-03-08陈静怡袁鹏程
陈静怡,袁鹏程
(上海理工大学 管理学院,上海 200093)
0 引言
网约车的快速发展正在悄悄改变着人们的出行方式,但是在为乘客出行提供便利的同时,也增加了道路的通行压力,造成了一定程度的交通拥挤。而网约车拼车运营模式可以将两个及以上路径相似的乘客分配给同一辆车,在车辆的容量限制内接送更多乘客。但是,在2020 年初,新型冠状病毒肺炎疫情突然爆发,由于该病毒具有极强的传染性且传播速度快,以往承担高运量乘客运输任务的公共交通成为具有较高病毒传播风险的载体。为了降低病毒在车内的传播风险,部分城市采取了调整公共交通运营时间及线路、降低车内人员数量等措施。例如武汉市在疫情爆发期暂停运营全市的公交、地铁和长途客运,为了保障社区居民的应急出行,武汉市交通运输局共征集6000 辆出租车和网约车,为居民应急出行提供服务。但是,在疫情期间,传统的网约车拼车调度方式暴露了管理缺陷,若不同风险等级的乘客被分配到同一辆车上会增加病毒交叉传播感染的风险,因此本文在传统的网约车拼车模型中考虑了乘客风险等级因素,在进行车辆匹配时禁止不同风险等级的乘客同乘一辆车。
目前有较多国内外学者对拼车问题进行了研究。车辆共乘问题(The Ride-Sharing Problem)是指具有相似行程和时间的乘客通过分摊油费、过路费等出行费用的方式共乘一辆车。Chen 等[1]使用自动驾驶汽车解决拼车问题;Ma 等[2]对峰时定价策略下的拼车用户均衡问题进行研究,通过定量分析得到了拼车可以降低出行者出行成本、有效缓解交通拥堵的结论。拼车问题(The Carpooling Problem,CPP)是基于私家车车主在往返工作场所途中想要接载同事的背景下提出的,这种出行方式成为减少拥堵地区私家车使用的一种可行方案。Guo 等[3]针对该问题提出一种基于蚁群算法的混合方法(HAC),用于解决多目的地的拼车问题。拨号叫车问题(The Dial-A-Ride Problem,DARP)最早是为老年人和残疾人提供的非盈利性质的门对门交通服务,通常以花费最少为目标。Cordeau[4]对DARP 问题的混合整数规划公式和分支切割算法进行介绍,并提出新的有效不等式来解决此问题。共享出租车问题(The Shared-Taxi Problem)可以最大限度地减少汽车中的空座,降低车辆运营成本以及乘客的出租费用。Hosni等[5]针对该问题提出一种拉格朗日分解法用于解决乘客分配问题以及规划出租车的最佳行驶路线。乘车匹配问题(The Ride Matching Problem)是一个多对多的问题,一名乘客可以在多辆车之间换乘,而一辆车可以搭载多名乘客。Masoud 等[6]设计了一种分解算法,通过解决多个较小问题来解决原始乘车匹配问题以达到最优。
疫情的突然爆发引起了众多学者对突发公共卫生事件下交通发展与管理的关注,目前针对疫情状态下交通问题的研究主要集中在两个方面:一方面是学者对疫情期间非常态下的交通应急管理研究,文献[7-10]分别从突发公共卫生事件下的交通管理对策、抗疫交通管理、非常态下的交通系统规划以及后疫情时代下的城市交通发展趋势等方面展开研究。针对疫情背景下大运量的公共交通管理研究,吴楠等[11]分别从疫情防控、刚性出行需求和公共交通客流回归等方面对疫情后武汉市的公共交通运营提出相应的应对策略;张宇等[12]建立了基于SEIR 模型的交通工具疫情传播模型与沿线路疫情传播模型,对新冠疫情通过交通线路向外传播扩散的过程进行了完整描述;李健等[13]提出一种面向传染病疫情防控的公共交通运行决策支持系统框架,其研究成果对公共交通的疫情防控具有实用价值;刘海平等[14]将室内病毒通过飞沫在空气中传播的理论应用于公共汽车车内空间,有针对性地提出公共汽车交通疫情防控应对策略。另一方面是学者对突发公共卫生事件下的交通需求及出行行为的研究,文献[15-17]分别对疫情期间公共交通系统的通勤客流、交通出行行为和城际交通运输需求进行分析。郑晏群等[18]依据疫情爆发时期不同交通出行方式的客流数据,分析了疫情爆发给不同交通模式带来的影响;吴娇蓉等[19]对疫情期间乘客的出行偏好进行调查分析,发现在疫情持续期间,民众对交通出行方式的暴露风险感知会影响合乘选择行为;高永等[20]对东北某市新冠疫情爆发前后一段时间内的网约车数据进行分析,发现受疫情影响,网约车的订单数量和司机出车数量均大幅减少,且与疫情的确诊人数呈正相关关系。
对上述文献进行综合分析后发现,非常规状态下的交通出行相关研究大多针对大运量的公共交通和轨道交通,而针对小运量交通,例如出租车、网约车和私家车的应对策略研究较少。传统的拼车模型主要考虑如何缩短乘客间的绕路距离、如何实现车辆收益增加与乘客出行费用减少的双赢局面,但在疫情反复出现的情况下,低风险乘客和高风险乘客若同乘一辆车会加速疫情的传播与扩散,增加交叉感染的风险。因此,为了优化新冠疫情背景下的拼车服务,本文提出考虑乘客风险等级的网约车拼车优化模型,对于低风险乘客,可为其提供正常的拼车服务,而高风险乘客禁止与他人同乘,接送高风险乘客的车辆在将乘客送达目的地后,需要前往防疫消毒点完成车辆消毒后才能重新接单。该措施可以有效防止因拼车导致病毒在车内传播,并确保其他乘客在拼车出行期间的安全。
1 问题描述
考虑乘客风险等级的网约车拼车调度优化问题场景如下:在城市某一区域内,有许多车辆和乘客分布在不同位置,疫情期间通过网约车平台提交拼车出行需求的乘客中,既有低风险乘客也有高风险乘客,每名乘客的出行需求包括上、下车点的位置坐标、乘车时间窗和乘车人数。每辆被派出接送乘客的网约车最大承载量一定,每辆车从其自身的车辆位置点出发前往乘客的上车点为其服务。网约车平台在对车辆进行派单时,依据乘客的风险等级采取不同的拼车方案。对于低风险乘客,网约车平台按照常规状态下的拼车方案进行分配,以保障车辆的总收益最大;对于高风险乘客,网约车平台在进行派单时要禁止此类乘客与他人同乘,同时运送过此类乘客的车辆要安排其前往最近的防疫消毒点进行消毒。网约车拼车场景如图1所示。

Fig.1 Scene of online ride-sharing under the epidemic situation图1 疫情状态下的网约车拼车场景
图1 展示的拼车场景中同时存在低风险乘客和高风险乘客,其中有3 名低风险乘客,2 名高风险乘客和2 个防疫消毒点。虚线圆圈内的数字表示节点编号,其中编号1-3分别表示3辆车的位置节点,节点编号4-6对应低风险乘客1-3,节点编号7、8 对应高风险乘客4、5,节点编号4-13表示5 名乘客的上下车位置节点,符号P1+、P1—分别对应节点编号4、9,表示乘客1 的上车点及其对应的下车点。为了保证路径约束的完整性,更加符合网约车实际运送情况,本文设置了虚拟车辆场站。图中虚线表示车辆与车辆场站之间的虚拟路径,假设车辆从车辆场站出发,完成运送任务后返回车辆场站,车辆与车辆场站之间的距离为0。场景图中既有低风险乘客也有高风险乘客,车辆1 运送高风险乘客4,车辆出发前往乘客的上车点(节点7),将其送往对应的下车点(节点12),之后前往防疫消毒点(节点14)进行消毒,具体的车辆行驶路径为1-7-12-14;车辆2运送参与拼车合乘的低风险乘客1~3,车辆出发依次前往乘客的上车点再将其送往目的地,具体的车辆行驶路径为2-4-5-6-11-10-9;车辆3 运送高风险乘客5,车辆出发前往乘客的上车点(节点8),将其送往对应的下车点(节点13),之后前往防疫消毒点(节点15)进行消毒,具体的车辆行驶路径为3-8-13-15。
2 模型建立
2.1 模型假设
为了简化问题,提出以下基本假设:接送乘客的车辆车型一致,不考虑车辆类别,车辆的最大承载量一致;不考虑乘客上、下车时花费的时间;任意节点之间的车辆行驶距离与行驶时间已知,车辆在接送乘客过程中匀速行驶,不考虑堵车和道路突发事件等,忽略道路交通的影响;一辆车可以服务多名乘客,但是每名乘客只能由一辆车提供服务,且中途不考虑车辆换乘情况;所有车辆都要从起始车辆场站出发到达终点车辆场站;区域内的网约车均接受运送高风险乘客,考虑到运送高风险乘客的车辆在完成运送任务后需要空驶前往消毒点进行消毒,因此凡是运送高风险乘客的网约车均可获得政府的额外补贴。
2.2 符号说明
在某一区域内有一些车辆和乘客分布在不同位置,假设在此区域内的乘客都接受拼车服务。nG表示要服务的低风险乘客数量;nR表示要服务的高风险乘客数量;nP表示所有乘客数量,包含低风险乘客和高风险乘客;nH表示在网约车平台中等待调度的车辆数量;nC表示区域内的防疫消毒点数量。用有向图G=(V,A)表示配送网络,其中表示区域内的所有节点,VO、VT表示车辆的起点和终点,意味着所有车辆都要 从VO出 发,最终回 到VT。A={
(1)参数。Qmax表示车辆的最大载客量;qi表示节点i处的乘客数表示车辆h在访问节点i后的载客量;Qh表示车辆h的载客量;dij表示从节点i到节点j的距离;ei表示节点i的最早开始服务时间;li表示节点i的最迟开始服务时间;tij表示从节点i到节点j的行程时间;c表示车辆运送乘客每km 的成本花费;f表示乘客接受车辆服务每km 所需支付的费用;W表示车辆产生的固定成本。
(3)变量。为车辆h在节点i的开始服务时间为0-1 变量,若车辆h经过弧
2.3 目标函数
不同于常规状态下的网约车拼车调度优化问题,在疫情期间的网约车拼车调度优化问题要考虑到运送高风险乘客的特殊性。为了提高车辆运送高风险乘客的积极性,政府应给予运输此类乘客的车辆一定的补贴,以达到总社会效益最大化的目标。因此,本文将从网约车平台角度出发,在满足乘客出行需求的前提下使总社会效益达到最大化。总社会效益与车辆运输收入、政府补贴费用、车辆运输成本和车辆固定成本4 个方面有关,具体目标函数如式(1)所示:
目标函数包含内容如下:
(1)车辆运输收入C1。此项收入中只考虑车辆在运营期间服务乘客时所获得的收益,不考虑网约车运营平台的补贴等其他收入,车辆运输收入只与被服务乘客上车点与下车点的距离以及乘客接受车辆服务每km 所需支付的费用有关,计算公式如式(2)所示:
(2)政府补贴费用C2。为提高网约车疫情期间运送高风险乘客的积极性,政府根据车辆服务高风险乘客的里程进行额外补贴,其中包括乘客的出行距离和车辆前往防疫消毒点的空驶里程,计算公式如式(3)所示:
(3)车辆运输成本C3。车辆运输成本是指车辆在运营期间产生的成本费用,只与车辆行驶距离和车辆行驶每km 的成本花费有关,此项不考虑车辆折损费用、维修费用和车辆保险等费用,计算公式如式(4)所示:
(4)车辆固定成本C4。车辆的固定成本包括车辆运营过程中产生的折损费用、维修费用和车辆保险等费用,固定成本与车辆行驶里程无关,计算公式如式(5)所示:
2.4 数学模型
本文构建的模型基于文献[4]中的拨号叫车问题,该问题最早是为老年人和残疾人提供非盈利性质的门对门交通服务,其在约束条件限制下,为指定了起始点和目的地的n名乘客设计车辆路线和时间窗,并规划m条车辆路径,以容纳尽可能多的乘客,一般在规划时以花费最小为目标。而本文构建的考虑乘客风险等级的拼车模型在该问题基础上增加了拼车乘客之间的约束、防疫消毒点约束等。与该问题的目标不同,本文从网约车平台角度出发,以车辆总收益最大化为目标,车辆总收益与车辆运输收入、政府补贴费用、车辆运输成本以及车辆固定成本有关。模型需要满足访问顺序约束、乘客唯一性约束、时间变量和负载变量一致性约束、车辆路径持续时间约束、时间窗约束、容量限制约束和特殊路径约束。基于以上内容构建的考虑乘客风险等级的拼车模型如式(6)-式(25)所示:
其中,式(7)是记录乘客是否被服务的约束;式(8)、式(9)保证每辆车的行驶路线从起始车辆段出发,在终点场站结束,设置此约束是为了方便构建模型,在文章中通过设置成本权值的大小使此约束不再是强约束;式(10)-式(12)是乘客唯一性约束,表示所有乘客最多可以被服务一次,乘客可能被服务,也可能不被服务,若一辆车服务了某个乘客,则其必须从上一个节点到达该乘客所在节点,并从该名乘客所在节点到达下一个节点。任何被服务的乘客都在其上车点上车并在其对应的下车点下车;式(13)是车辆的消毒站点约束,保证消毒站点可以为多辆车提供服务;式(14)、式(15)保证只有接送过高风险乘客的车辆才可以到消毒站点消毒;式(16)-式(18)表示高风险乘客不能进行合乘;式(19)、式(20)是时间变量和负载变量的一致性约束;式(21)是车辆路径持续时间约束,车辆路径持续时间不能超过车辆在路径上的最大持续时间;式(22)是时间窗约束条件,表示车辆在节点处的开始服务时间要在最早开始服务时间与最迟开始服务时间之内,以满足乘客的时间窗要求;式(23)是车辆容量限制约束;式(24)、式(25)是0-1决策变量。
3 算例分析
3.1 算例描述
由于缺少与拼车调度优化模型相关的经典算例,本文根据模型的需要对数据进行合理假设,利用MATLAB 软件随机生成车辆点、乘客点以及防疫消毒点的位置坐标和时间窗等相关数据。在算例中共有20 名乘客,其中高风险乘客5 名,低风险乘客15 名,提供拼车服务的车辆共有5辆。假设存在两个虚拟节点,分别作为提供拼车服务车辆的起点和终点,车辆与乘客点的位置坐标都是随机且独立、均匀分布在[0,100]×[0,100]的区域内,用节点间的欧几里得距离表示行程时间tij和行程距离dij。乘客接受车辆服务所需支付的费用f为10 元/km,车辆运送乘客的运输成本c为1 元/km。将车辆的固定成本W设置为15 元,每辆车的最大载客量Qmax=3,车辆场站的坐标设为原点(0,0)。各个节点位置坐标以及最早开始服务时间和最迟开始服务时间的数据信息如表1所示。
3.2 算例结果
为了更好地比较是否考虑乘客风险等级对网约车调度优化模型产生的影响,将传统网约车拼车问题即未考虑乘客风险等级的网约车拼车服务视为未优化方案,将考虑乘客风险等级的网约车拼车服务视为优化后的方案。本文基于区域内提出拼车请求的乘客点数据和提供服务的车辆数据对未考虑乘客风险等级的网约车拼车模型进行求解,未考虑乘客风险等级的网约车拼车模型是在DARP模型基础上,将目标函数替换为社会总效益最大。利用Lingo 软件进行求解,得到未优化的车辆行驶路径如表2所示。
为了能够客观地比较优化前后车辆路径的变化,在原有算例数据中添加防疫消毒点的相关数据,将区域内原有乘客划分为高风险乘客与低风险乘客两类,乘客的其他相关数据保持不变,得到一个包含5 辆车、15 名低风险乘客和5 名高风险乘客的节点数据以及时间窗要求的算例。利用Lingo 软件求解考虑乘客风险等级的网约车拼车调度优化模型,得到如表3所示的优化后的车辆行驶路径。
对比优化前后的车辆行驶路径可以发现,在对乘客进行风险等级划分后,以车辆2 的行驶路径为例,优化后的方案中不同风险等级的乘客7 与乘客18 不再同乘一辆车;以车辆5 的行驶路径为例,优化后的方案中车辆在将编号为19 的高风险乘客送往下车点后,前往防疫消毒点48 进行消毒,符合模型中的条件约束。但是对比表2 可以看出,优化后的车辆空驶距离增加,例如车辆5 的空驶距离从4.3km 增加至11.2km,车辆运输成本也相应增加。考虑到运送高风险乘客会增加车辆的空驶距离,为了提升车辆运送高风险乘客的积极性,政府应给予运送高风险乘客车辆一定的补贴。本文在同一算例场景中对不同补贴金额下车辆的行驶路径进行分析,得到结果如表4 所示。政府对运送高风险乘客的车辆补贴为r,当r=0(即没有补贴)时,场景中5 辆车里只有一辆车运送高风险乘客,其他4 辆车运送的均为低风险乘客;当r=5 时,在同样的场景中,有两辆车运送高风险乘客;当r=10 时,在同样的场景中,有3辆车运送高风险乘客。

Table 2 Vehicle driving path without considering passenger risk level表2 未考虑乘客风险等级的车辆行驶路径

Table 3 Vehicle driving path considering passenger risk level表3 考虑乘客风险等级的车辆行驶路径
从上述算例结果可知,当不同风险等级的乘客在同一拼车场景中时,根据本文构建的考虑乘客风险等级的网约车拼车模型对车辆与乘客进行分配,得到的结果中没有出现不同风险等级的乘客同乘一辆车的情况,且参与拼车的低风险乘客数量均满足车辆的最大载客量;运送高风险乘客的车辆每次只运送一名乘客,以车辆5 运送编号为19 的高风险乘客的行驶路径为例,具体车辆行驶路径为:车辆5—乘客19 的上车点(25)—乘客19 的下车点(45)—防疫消毒点(48)—车辆5 终点,从其行驶路径中可以看出,在将乘客送往对应的下车点后,车辆会前往防疫消毒点进行消毒;不同金额的政府补贴会影响乘客与车辆的匹配结果,补贴金额越高,车辆运送高风险乘客的数量越多。在设定的场景中,不论是低风险乘客还是高风险乘客,最终得到的分配结果均符合模型中的设定,通过此小规模算例可以证明本文所构建模型的有效性。
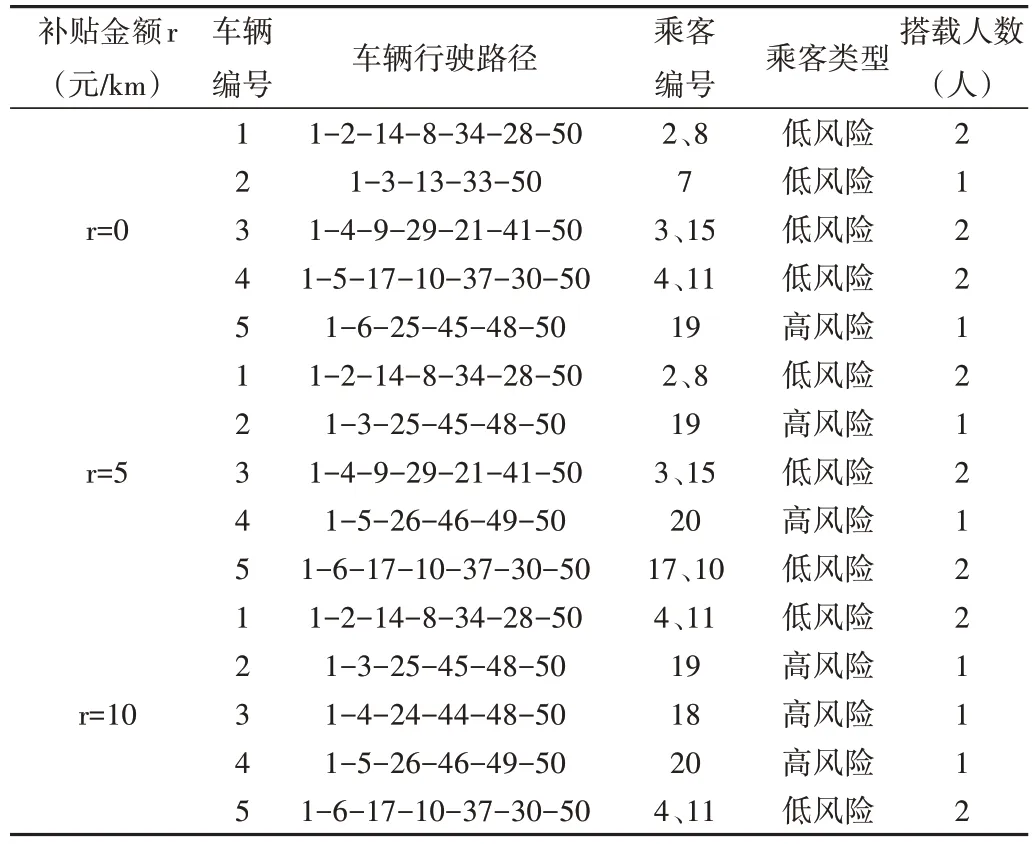
Table 4 Driving routes of vehicles under different subsidies表4 不同补贴金额下车辆行驶路径情况
4 结语
新冠病毒疫情的反复影响着人们的日常生活,导致居民每一次出行都处于风险之中。本文构建了基于乘客风险等级的拼车调度优化模型,并综合考虑了拼车场景中同时具有低风险乘客和高风险乘客时的拼车方案,利用Lingo 软件对算例求解,通过比较考虑乘客风险等级的车辆路径和未考虑乘客风险等级的车辆路径两个方案验证了模型的有效性,可为疫情下的网约车拼车优化问题提供理论依据。当拼车场景中同时具有低风险乘客和高风险乘客时,运用该模型对乘客进行分配,能够根据乘客风险等级提供不同的拼车方案,以此降低乘客在拼车出行过程中感染病毒的风险。同时作为疫情期间的应急保障车辆,政府应给予网约车一定的补贴。本文对不同金额政府补贴下车辆运送高风险乘客的数量进行对比,发现不同的补贴金额会影响车辆是否接送高风险乘客的决定。若补贴过低,可能会出现车辆接送高风险乘客的积极性不高,保障服务达不到预期效果;若补贴过高,可能会出现车辆抢单的情况,造成政府资金的浪费,因此政府补贴金额的标准如何确定将作为下一步的研究方向。
