洪水波周期性对堤防稳定性影响的数值模拟

杨 菁

(南昌市城市防洪事务中心，江西 南昌 330000)

1 研究方法

1.1 灵敏度分析

本文应用灵敏度分析方法确定对堤防状态影响最大的洪水波参数。分析可分为三个阶段，分别计算灵敏度比、灵敏度评分和总相对灵敏度。

灵敏度比ηSR可以描述为模型输出的百分比变化除以输入变量的单位变化，如式(1)：

(1)

式中：f(xL,G)为利用给定输入参数xL,G的变化值后得到的输出变量值；f(xm)为利用给定参数的参考值xm后得到的模型输出参考值。

对于每一个考虑的参数，本文计算了四个灵敏度比。可以分为两类：局部和全局。对于局部类别，输入参数值xL在随机集的一个小区间内变化。在全局灵敏度比中，给定参数xG的输入值在随机集的整个范围内变化(如图1)。

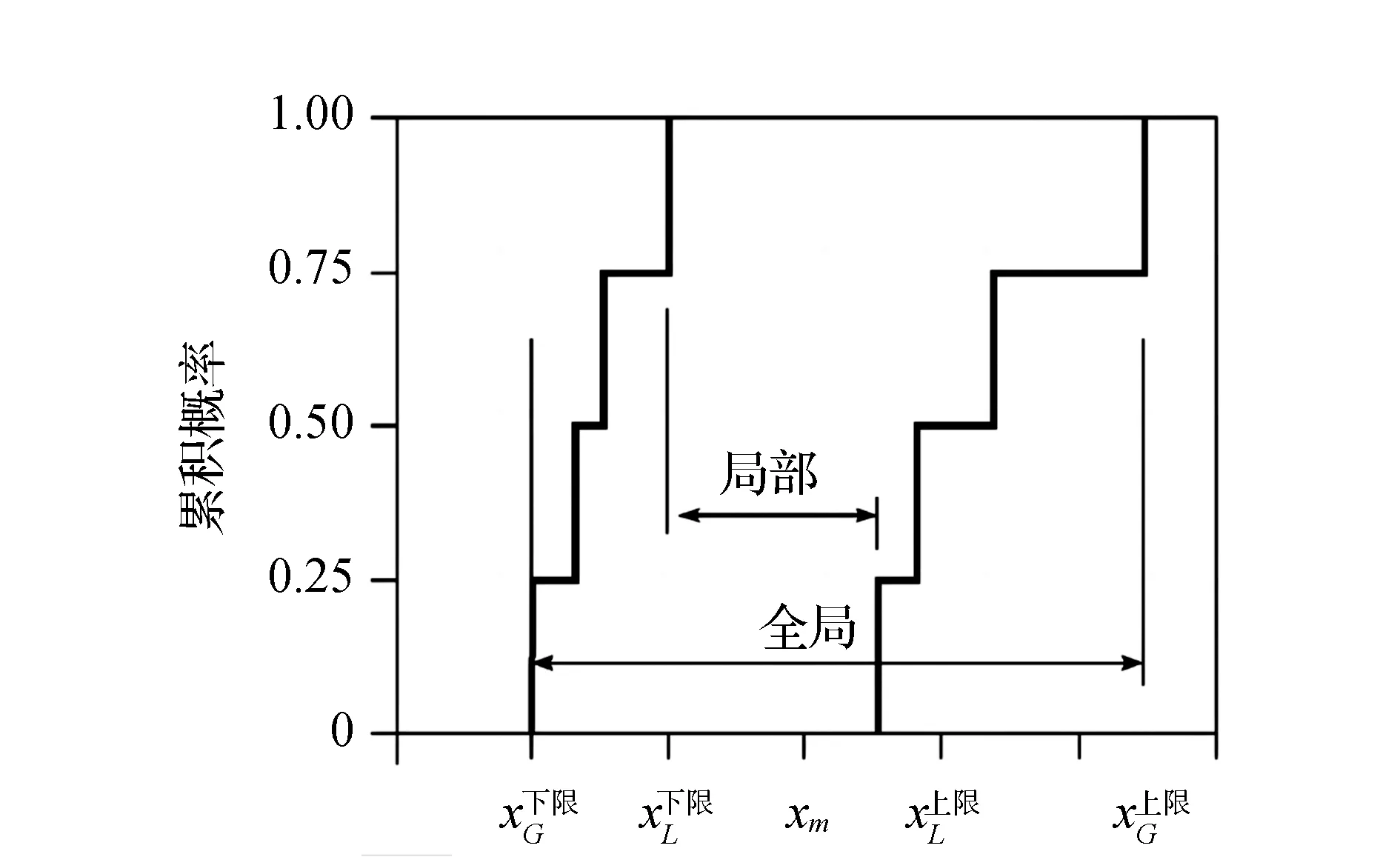
图1 局部和全局范围区间的灵敏度比图示

灵敏度评分ηSS是评估给定模型不确定性的一种方法，可以通过对输入参数中的灵敏度比值进行归一化和加权来获得。如式(2)：

(2)

归一化过程使灵敏度评分独立于给定参数的输入值单位。灵敏度评分ηSS,i(i=1,2,…,N)是针对考虑的所有N个基本参数计算的。

每个输入变量的总相对灵敏度α(xi)计算为每个输入参数ηSS,i在位移、力、孔隙压力或安全系数等相应结果上所有灵敏度评分(局部和全局范围)的总和。可以写为公式(3)：

(3)

一旦确定阈值，总相对灵敏度可用于确定哪些参数对安全系数有显著影响。通常认为5%～10%的阈值是合适的。

1.2 洪水波周期性建模

利用二维显式有限差分软件FLAC[1-7]对洪水路堤状态的影响进行了数值模拟。该软件允许执行机械—流体和流—热耦合过程用于堤防稳定性建模。

(1)地质模型描述。本文对建造的实验路堤进行数值计算。与实验路堤横截面一致的假定数值模型几何结构如图2所示。假设模型的材料参数如表1所示。

图2 用于数值计算的地质模型几何结构(单位：m)

表1 材料参数

(2)洪水过程灵敏度分析说明。在灵敏度分析中，研究了两种类型的洪水过程：单次洪水波和双次连续洪水波。两个参数区间是独立确定的。第一组是通过对研究流域历史洪水的分析确定的。第二组是在已有经验和文献研究[8-9]的基础上对水位变化速率和水位高度应用了某些限制值。

(3)数值计算。对于上述洪水过程的灵敏度分析，需要21个确定性模型。在每个模型中，采用每个参数局部和全部范围区间的下限或上限。其余4个参数的值用参考值固定。数值模拟的结果为假定数值模型中每个计算节点上的孔隙压力分布和垂直位移。对所有21个洪水过程开发情景的值进行处理，以确定5个基本参数中哪一个最重要，对输出变化影响最大。

2 洪水波参数灵敏度分析结果

对堤坝上单次洪水波和双连续洪水波进行了洪水波参数灵敏度分析。图3～图9显示了所有计算节点的分析结果，表明了基本洪水波参数对路堤内孔隙压力分布和垂直位移的影响。这些曲线图对应于上述灵敏度评分值(见式(2))，还给出了与总相对灵敏度(见式(3))相对应的孔隙压力分布和垂直位移的灵敏度分析结果。在曲线图中，灵敏度评分和总相对灵敏度值小于10%。

2.1 单次洪水波后的灵敏度结果

对21种情景进行了不同持续时间的洪水过程数值模拟。洪水波模型的持续时间从9～14 d不等。使用孔隙压力和垂直位移分布的灵敏度评分以及总相对灵敏度进行灵敏度分析，结果分别如图3～图5所示。

图3 单次洪水波参数对孔隙压力分布的灵敏度评分值

图4 单次洪水波参数对垂直位移分布的灵敏度评分值

图5 单次洪水波参数的总相对灵敏度值

对孔隙压力场和垂直位移建模以获得灵敏度评分值分布，可以观察到水位上升速率对其没有影响。这也反映总相对灵敏度值实际上<5%。孔隙压力模拟结果的灵敏度评分表明，影响最显著的洪水波参数是连续洪水波后的水位和时间间隔。但在一些路堤区域，水位下降速率和持续时间也是显著值。对堤防垂直位移进行了相同计算，结果表明，可以观察到水位下降速率和持续时间影响的区域。图5显示，当接受10%的阈值时，堤防稳定性分析中有四个最重要的参数，即高水位持续时间、高水位下降速率、连续洪水波之间的时间间隔和水位。

2.2 双连续洪水波后的灵敏度结果

将洪水波参数灵敏度分析的研究扩展到双洪水波的情况。这种分析能够估计低水位持续时间参数对路堤内孔隙压力和垂直位移值分布的实际影响。与单次洪水过程的情况一样，不同的洪水波模拟持续时间适用于所有21种情景。在这种情况下，洪水过程的最短情景时间为18 d，而最长情景时间为28 d。图6～图8分别给出了使用孔隙压力和垂直分布的灵敏度评分以及双洪水波周期的总相对灵敏度分析结果。

图6 双连续洪水波参数对孔隙压力分布的敏感性评分值

图7 双连续洪水波参数对垂直位移分布的敏感性评分值

图8 双连续洪水波参数的总相对灵敏度值

灵敏度分析在双连续洪水波模型中的应用结果也表明，水位上升速率对堤防状态影响不显著。其值是固定的，不应包括在洪水波情景的确定中。双连续洪水波影响的灵敏度分析表明，水位下降速率和高水位持续时间对孔隙压力结果的影响大于单次洪水波的计算结果。这是第一次洪水波造成的现有饱和度的结果。图9显示了单次洪水波和双连续洪水波计算的总相对灵敏度值之间的差异。

图9 单次洪水波和双连续洪水波总相对灵敏度值的差异

差值图表明，四个参数对剩余饱和度都很敏感。两种情景下差异的位置通常在路堤的同一部分。在所有四个重要的洪水过程参数中，水位曲线图达到最高值。相对于其他参数来说，在路堤的最大面积上计算出的单次洪水波和双连续洪水波的水位总相对灵敏度值差异也很明显。

3 结 论

(1)灵敏度分析方法对于检测对垂直位移和孔隙压力分布影响最大的路堤位置非常实用。

(2)对单次洪水波情景和双连续洪水波进行灵敏度分析，得出了关于洪水波参数重要性的相同结论。两种类型的情景(单次洪水波、双连续洪水波)都表明水位上升速率对堤防状态影响不显著。确定了对堤防状态影响最大的洪水波四个重要参数为高水位持续时间、高水位下降速率、连续洪水波之间的时间间隔和水位。

(3)灵敏度分析检测了总相对敏感度值的最大差异，得出两种情景下差异的位置通常在路堤的同一部分，即为路堤内最易受到连续洪水波影响的区域。