基于ARIMA-GM 的石油价格预测模型及实证分析

杨岚清

（新疆财经大学 统计与数据科学学院， 新疆 乌鲁木齐 830012）

0 引言

石油的用途主要用作燃料油和汽油，其价格变化在很大程度上作为市场信号会影响到其他相关行业产品价格水平。客观分析和预测未来石油价格，对于把握我国石油经济走向十分重要。目前灰色预测被广泛用于各领域之中，根据前人预测方法的回顾，预测的算法众多，如多元线性回归、时间序列分析、支持向量机、神经网络等。在时序变化下短期预测，采用灰色预测所需样本少，不需计算均值、方差等特征量。目前灰色预测被广泛用于各领域之中，陈磊等[1]将GM（1，n）应用于电力负荷预测方面；蒋红霞等[2]通过全信息新陈代谢的GM（1，1）灰色预测模型对双流县方面进行了预测；在石油价格预测方面，多尝试于使用不同的模型以求更准确的预测，针对单一模型预测精度不高等问题，本文基于GM预测与ARIMA 模型进行预测工作，构建ARIMA-GM模型。

1 ARIMA-GM 混合模型介绍

ARIMA 是一种用于时间序列分析和预测的经典方法，ARIMA 全称为自回归综合移动平均模型（Autoregressive Integrated Moving Average Model）。其本质是对原始时间序列进行数据拟合，然后利用该拟合模型对未来时间序列进行预测。综合考虑自回归过程、移动平均过程和差分处理后建立的模型，得到ARIMA（p，d，q）模型，这是ARIMA 模型的基本形式。其中，p、d、q 分别表示AR、I、MA 的阶数。GM灰色预测是一种基于灰色系统理论的预测方法，灰色理论是建立在非随机的少样本数据上进行研究的，它是从黑箱计算机模型的观念出发，奠定了处理小样本非线性问题的基础，用建立数据之间的数量联系和质量关联模型的方法，来对样本数据进行分析和预测。在GM（1，1）模型中，基于时间段数据序列，通过GM（1，1）微分方程，建立规律序列。根据规律序列推理出等周期累加生成序列，然后分别求得半平均值和邻值平均值，从而预测未来一定周期内的数值。它通过对时间序列数据的特性进行分析，建立相应的灰色模型，预测未来一定周期内的数值，具有较好的预测精度和可解释性[3-4]。

ARIMA-GM混合模型是将灰色系统理论与自回归移动平均模型相结合，用于时间序列的预测。相比于自回归移动平均模型模型，混合模型具有以下优势：

1）对于小样本的预测具有更好的鲁棒性：ARIMA模型需要很多数据点才能拟合出准确的模型，而混合模型运用灰色系统理论可以在少量数据点的情况下进行预测，具有更好的预测鲁棒性。

2）对于非线性趋势的时间序列具有更好的适应性：混合模型还特别适用于非线性趋势的时间序列预测，比如呈现出指数增长或下降趋势的数据。

3）可以解决样本数据的不平衡性：在现实中，由于各种原因，往往出现时间序列数据中的贫瘠区域。针对这种情况，ARIMA 模型可能会出现过拟合或欠拟合现象，导致预测效果不佳，混合优于ARIMA 模型，具有较好的适应能力[5-6]。

4）混合模型可以克服ARIMA 模型的一些限制，对于小样本、非线性趋势或不平衡数据的时间序列预测方面具有优势，因此在石油价格预测等方面也有一定的应用价值。模型公式为：最终预测值=α*ARIMA 预测值+β*GM 预测值，其中，α 和β 取值范围分别为［0，1］，α+β=1。

2 实证分析

2.1 预测数据

本文实证研究数据部分选取了2020 年9 月—2022 年7 月的国际市场主要原油现货平均价格（欧佩克价格）进行分析和预测。在石油价格时间序列分析的实践中，如果一个时间序列并不是白噪声序列，就可能存在可以被分析或预测的模式和关联，可以进行进一步研究分析检验是否为白噪声序列。

2.2 数据描述性统计

根据国家统计局发布的数据，2022 年我国石油消费量为7.1 亿t 标准煤，同比增长3.6%。据国际能源署（IEA）统计，2019 年我国石油消费占全球消费量的14.3%，而进口石油占全球进口量的20.2%。

图1 是对2018—2023 年石油月价格的刻画分析。2018—2023 年间石油价格出现了较大波动。值得注意的是，2018 年石油价格持续上涨，最高价达到79.39 美元/桶，但自同年11 月份起开始下跌，至2019年4 月份降至70.72 美元/桶。接下来至2020 年5 月份，全球经济停滞，原油需求大幅下降，导致全球油价暴跌，2020 年4 月份油价最低，降至仅有17.66 美元/桶，之后虽然有所回升，但波动仍然明显。2021 年10月—2022 年3 月，则出现了第二次缓慢但稳定地上涨，最高价达到113.61 美元/桶，而后价格再次下滑。截至2023 年3 月，石油价格降至78.45 美元/桶。

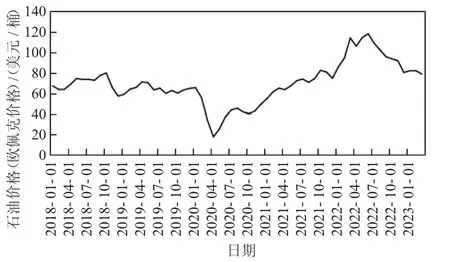
图1 石油月价格刻画

2.3 ARIMA 模型预测结果及分析

2.3.1 ARIMA 模型DF 残差检验

首先针对序列进行白噪声检验和残差检验。取2020 年9 月—2022 年3 月的数据建立模型，剩余的4 个月作为模型的预测实验。自动匹配拟合优度最高的模型及模型参数，检验通常需要进行残差分析。残差分析是评估模型拟合效果的一种常用方法，可以用来检查模型是否存在误差和随机波动。在ARIMA 模型中，一阶差分后的序列数据应当是平稳的，因此需要检查残差序列是否存在随机波动和自相关性。对于ARIMA 模型需要进行残差分析来检验模型的拟合效果和统计显著性。本文中Df是指残差的自由度，Df计算公式为：N-p-1，其中N 表示样本的数量，p 表示回归模型中变量的数量。用于计算残差标准误，以评估模型的拟合效果和预测精度。

系统基于AIC 信息准则自动寻找最优参数，模型结果为ARIMA 模型检验表，如表1 所示，从Q 统计量结果分析可以得到：Q6 在水平上不呈现显著性，不能拒绝模型的残差为白噪声序列的假设，同时模型的拟合优度R2为0.895，模型表现优秀，模型基本满足要求。得到的结果不能拒绝模型的残差为白噪声序列的假设意味着模型能够很好地利用已有数据对未知数据进行预测，并且残差的序列已经被有效地拟合。同时模型的拟合优度R2为0.895，这意味着该模型能够解释大约89.5%的数据方差，表现较为优秀。

2.3.2 ARIMA 预测结果及分析

2022 年4 月—7 月的石油预测价格如表2、图2所示。

表2 ARIMA 预测结果

将ARIMA 模型的预测值与真实值进行对比，在2022 年4 月份的预测值117.12 与真实值105.64 之间的误差为10.91%，在2022 年5 月份的预测值120.629 与真实值113.93 之间的误差为5.89%，在2022 年6 月份的预测值124.139 与真实值117.72 之间的误差为5.46%，在2022 年7 月份的预测值127.648 与真实值108.55 之间的误差为17.63%。平均误差为9.95%。这表明ARIMA 模型预测结果与真实值之间存在一定的误差。其中一些误差可能是由于模型中未捕捉到的外部因素造成的，也可能是由于训练数据集本身的缺陷导致的。因此，接下来构建更优模型进行预测，并根据需要进行相应的修正和改进。

2.4 GM模型预测结果及分析

2.4.1 GM（1，1）模型级比检验

取2020 年9 月至2022 年3 月的数据建立模型，剩余的4 个月作为模型的预测实验。针对石油价格这一时间序列数据，序列值是指时间序列中各个时间点的数值，而级比值则是序列值之间的比率也称为相对大小。级比值通常用于识别和测量不同时间点之间的变化幅度。在石油价格时间序列中，本文将最早的序列值定义为基期（即100%），并将其级比值设置为1。然后对于后续的序列值，其级比值是相对于基期的值。表3 为石油价格GM 预测GM（1，1）模型级比值表。

表3 展示了序列值和级比值。若所有的级比值都位于区间（e-2/(n+1)，e2/(n+1)）内，说明石油价格数据适合模型构建。若不通过级比检验，则对序列进行“平移转换”，从而使得平移转换后序列满足级比检验。结果显示，原始数据并没有通过级比检验，因此进行平移转换，即在原始值基础上加入平移转换值114.00，最终平移转换后的数据级比检验值均在标准范围区间［0.913，1.095］内，意味着本数据适合进行GM（1，1）模型构建。

2.4.2 GM模型构建

一般后验差比值C 值小于0.35 则模型精度高，C值小于0.5 说明模型精度合格，C 值小于0.65 说明模型精度基本合格，如果C 值大于0.65，则说明模型精度不合格。从表4 分析可以得到，后验差比值为0.089，模型精度高。采用处理后的时间序列数据进行模型拟合，以寻找最佳拟合参数。拟合表记录了不同参数下的模型误差和拟合精度指标结果，用于寻找最佳的模型参数。

表4 GM 模型构建值

2.4.3 GM预测结果及分析

表5 展示了灰色预测模型的拟合结果表。相对误差值越小越好，一般情况下小于20%即说明拟合良好。模型平均相对误差为6.108%，意味着模型拟合效果良好，说明灰色预测模型能够较为准确地拟合数据，并对未来趋势进行预测。

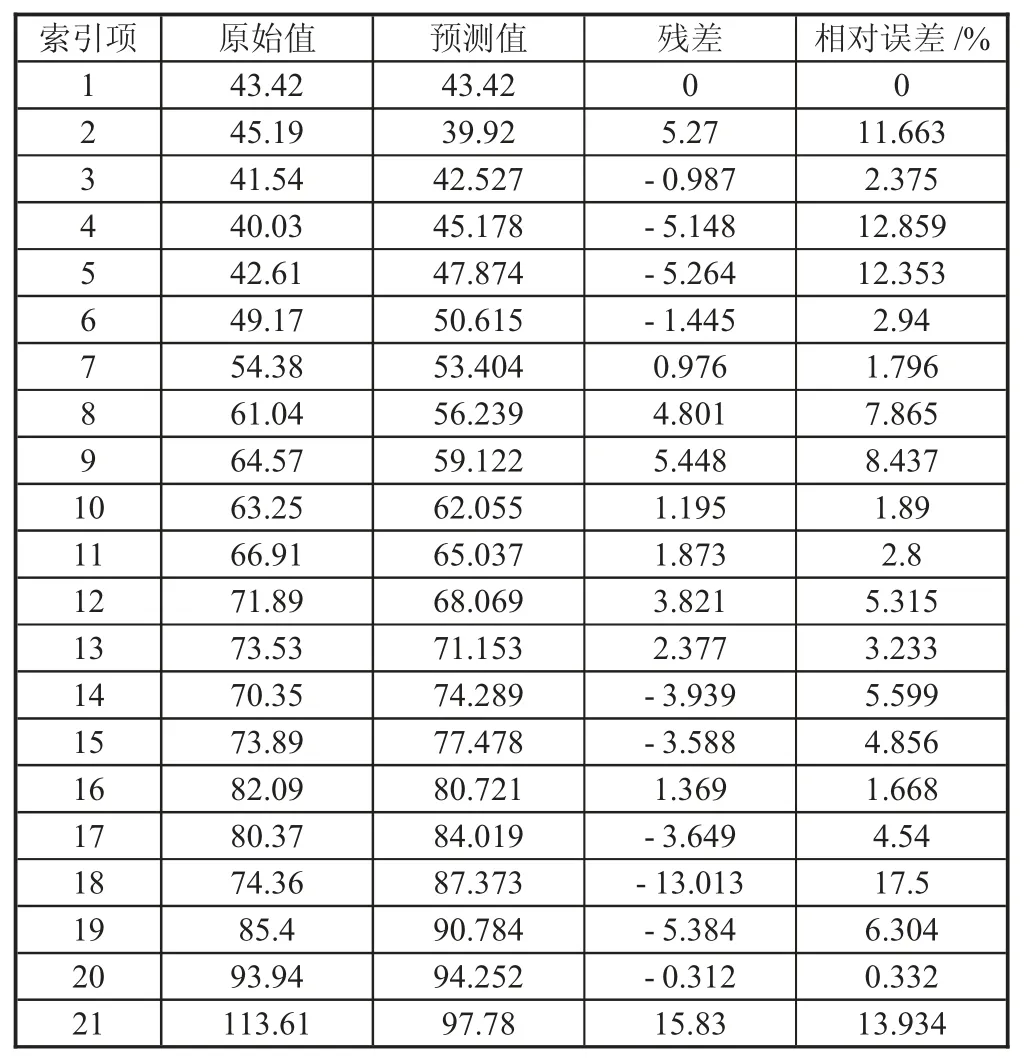
表5 GM 预测模型的拟合结果表

从表6、图3 可以看出，使用GM 模型预测了油价未来四期的值，并将预测值与真实值进行了对比。根据对比结果，可以发现预测值与真实值之间存在一定的误差。平均误差的计算公式为（预测值- 真实值）/真实值×100%。在这个问题中，平均误差的计算结果为-3.99%。向后2 期、向后3 期和向后4 期的平均误差分别为-8.08%、-7.64%、3.64%。综合平均误差为5.79%。通过对比可以发现，预测值与真实值之间的误差存在一定的波动。但其预测误差相对较小。这意味着GM 模型能够从历史数据中得出较为准确的预测结果，并且在实际应用中，这种误差是可以接受的，其预测效果是否长期稳定还需要进行更深入的研究和实证分析，需要持续监测预测值与真实值之间的误差，及时对模型进行修正和改进，提高预测精度和稳定性。

表6 GM 预测结果

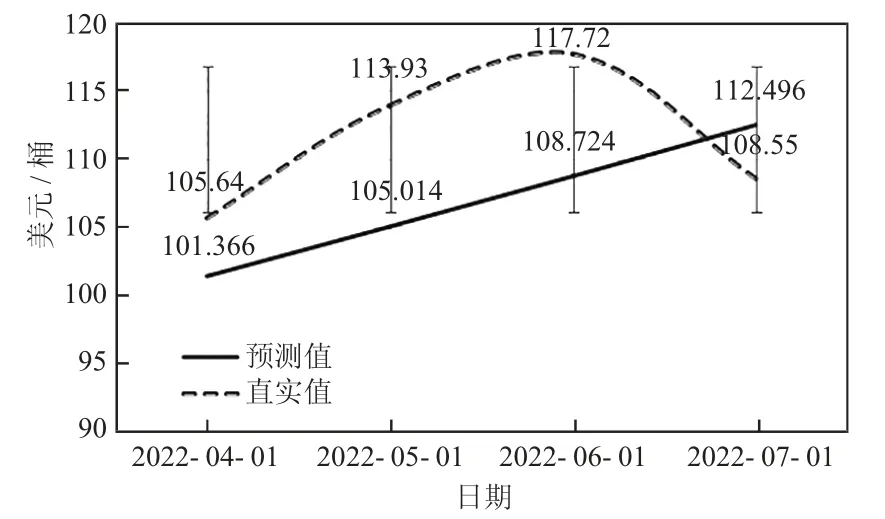
图3 GM 真实值与预测值对比

2.5 ARIMA-GM混合预测模型

采用加权法将ARIMA 和GM的预测结果进行综合，加权公式为：综合预测值=0.3*ARIMA 预测值+0.7*GM预测值。得到的后4 月的综合预测值如表7所示。

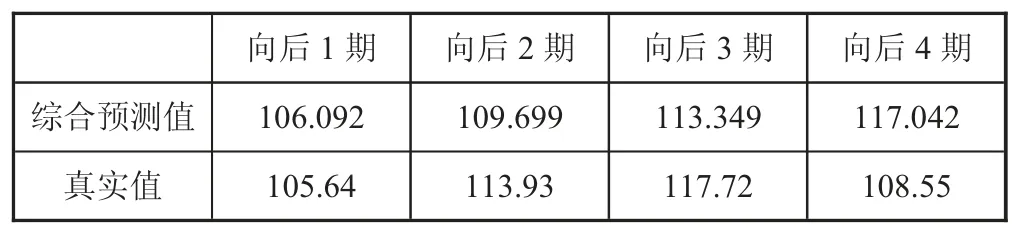
表7 混合模型预测结果

根据提供的表格数据比较预测值和真实值可以发现，在向后1 期和向后4 期，混合模型的预测值分别高于和略低于真实值；而在向后2 期和向后3 期，混合模型的预测值分别低于和略高于真实值。此外，对以上数据进行进一步分析，可以计算出预测误差。以向后1 期为例，预测误差为0.43%，其余三期的预测误差也很小，都在1.5%以内。这说明综合预测模型相对于单一模型拥有更低的预测误差，具有更好的预测能力。

综合预测模型的平均预测误差仅为3.92%。混合模型预测值与真实值之间的吻合度更高。通过图4 可知，也能够看出混合模型的预测值与真实值之间的吻合度更高，这也验证了混合模型的预测效果较好的结论。混合模型综合预测模型预测了油价未来四期的值。比较预测值和真实值可以发现，整合后的综合预测模型的预测误差较小，平均预测误差仅为3.92%。这说明综合预测模型在预测未来油价方面比单一模型更准确。此外，混合模型还可以灵活地根据实际情况选择最佳模型进行预测，提高了预测的准确性和可靠性。

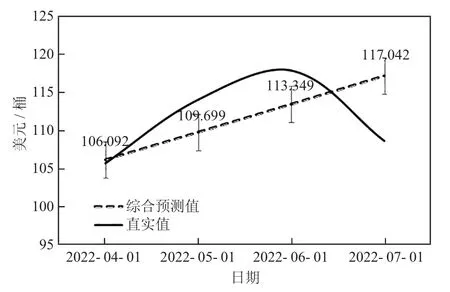
图4 综合预测结果对比

同时由图1 可知，2018—2023 年的月度数据的时间序列预测过程中，长期趋势较不稳定，并存在周期波动混合模型还考虑了历史数据的不均匀性和不确定性因素，从而提高了预测精度。混合模型根据历史数据的自相关性、季节变化和白噪声等特征，建立了合适的模型结构，以捕捉时间序列的长期趋势、周期性和残差等信息。

3 结论

提出了基于ARIMA-GM 的石油价格预测方法，考虑了时间序列自身特性和对石油价格的多种影响因素，并对国际市场主要原油现货平均价格（欧佩克价格）进行了预测实证分析.实验结果表明，ARIMA-GM方法可以对石油价格的预测误差大幅降低，预测精准度提高。然而，石油市场行为的不确定性和复杂性依然存在，需要通过进一步的研究和解决，才能更好地实现石油市场的可持续发展。