构网型储能变流器并网系统SISO环路增益建模与重塑控制

郭小龙 杨桂兴,2 张彦军 周 毅

构网型储能变流器并网系统SISO环路增益建模与重塑控制

郭小龙1杨桂兴1,2张彦军1周 毅3

（1. 国网新疆电力有限公司，乌鲁木齐 830063； 2. 新疆大学电气工程学院，乌鲁木齐 830046； 3. 四川大学电气工程学院，成都 610065）

储能变流器是连接储能介质与电网的核心装备，当变流器控制参数与电网阻抗不匹配时，易出现失稳现象。为了分析构网型（GFM）储能变流器的并网稳定性，本文提出一种功率同步环主导的单输入单输出（SISO）环路增益模型，结合频域控制理论中的幅值、相位裕度实现对GFM储能变流器并网系统小干扰稳定裕度的量化分析，结果表明GFM储能变流器在弱电网下具有良好的稳定性，但是在强电网下系统稳定裕度不足；因此，提出一种基于虚拟阻抗的GFM储能变流器并网系统环路增益重塑控制策略，并研究虚拟电阻、虚拟电感对系统抗噪声干扰、稳态运行点及稳定性的综合影响规律，给出参数的整定建议。最后，通过Matlab/Simulink仿真模型证明了理论分析的正确性和有效性。

构网型变流器；储能；小扰动稳定性；虚拟阻抗

0 引言

为实现我国“双碳”目标，越来越多的风电、光伏等新能源接入电力系统，在其提供优质、绿色能源的同时，由于新能源发电的强波动性和强随机性，也带来了新能源消纳难的问题[1]。

为了解决绿色电力的消纳和存储问题，越来越多的储能电站投入运行，如电化学储能电站[2]、抽水蓄能电站[3]、飞轮储能电站[4]等。其中，储能变流器是连接储能装置与电网的核心装备。早期，储能系统主要采用锁相环同步型的跟网型（grid-following, GFL）变流器并入电网，通过公共连接点（point of common coupling, PCC）处的电压定向，实现储能变流器的单位功率因数运行[5]。然而，已有研究指出采用GFL变流器的储能系统存在两个缺点：①GFL变流器对外呈现电流源特性，并且通常工作在最大功率输出模式，不具备对电网电压、频率的主动支撑能力[6]；②此外，在弱电网条件下，锁相环与电网阻抗交互，易引发振荡[7]。因此，为了增强储能系统对电网的主动支撑及在弱电网下的稳定运行能力，已有研究提出采用构网型（grid- forming, GFM）变流器的储能系统[6]。

目前，GFM变流器主要的控制方式包括下垂控制、虚拟同步机和虚拟振荡器控制[8]。文献[9]将采用GFM变流器的储能系统与同步发电机进行类比，指出GFM储能可模拟同步发电机，对外呈现电压源特性，具备调频、调压能力。在GFM储能并网系统稳定性方面，文献[10]针对采用虚拟同步机的储能并网系统，建立正负序阻抗模型，指出采用GFM变流器的储能并网系统对弱电网的适应能力更强。文献[11]建立GFM变流器dq阻抗模型，并基于简化后的环路增益模型指出GFM变流器在强电网条件下无法稳定运行。然而，无论是正负序阻抗模型还是dq阻抗模型都属于多输入多输出（multiple input multiple output, MIMO）模型，难以像单输入单输出（single input and single output, SISO）模型那样量化参数对GFM储能并网系统稳定裕度的影响。

此外，为了增强GFM变流器在强电网下稳定运行的能力，已有研究提出了多种改进的控制方法。文献[12]通过在GFM变流器的功率同步环节中引入锁相环，提出混合同步控制策略，但是锁相环的引入会恶化GFM变流器在弱电网下的适应能力。文献[13]和文献[14]分别提出GFL与GFM虚拟并联的控制策略及基于∞控制的同步控制策略，用以实现不同电网强度下的最优控制，但是其算法较为复杂。相较于上述方法，将虚拟阻抗控制引入GFM变流器控制中用以增强GFM变流器在强电网下的稳定性，具有明确的物理意义且实现简单[15]。其中，虚拟阻抗控制参数的合理选取是确保该方法可行的重要前提。

针对现有研究的不足，本文首先针对GFM储能变流器并网系统，建立其单SISO环路增益模型，研究不同电网阻抗对GFM储能变流器并网系统小干扰稳定裕度的影响规律；其次，提出一种基于虚拟阻抗的GFM储能变流器并网系统环路增益重塑控制策略，并研究虚拟电阻、虚拟电感对系统抗噪声干扰能力、稳态运行点及稳定性的综合影响规律，给出参数的整定建议；最后，通过Matlab/Simulink仿真模型研究理论分析的正确性和有效性。本文研究对新型电力系统中储能并网系统的稳定控制及参数整定具有一定的参考意义。

1 构网型储能并网系统简介

本文的研究对象为图1所示的构网型储能并网系统，储能介质采用锂电池。锂电池组经串并联后，通过Buck-Boost双向变换接入DC-AC并网变流器，交流侧采用0.4kV/35kV变压器并入电网。由于DC-AC变流器具有隔离作用，且直流侧具有较大的支撑电容，因此可将DC-DC模块等效为理想的直流电压源。在充/放电模式下均保证中间直流环节电压为700V。

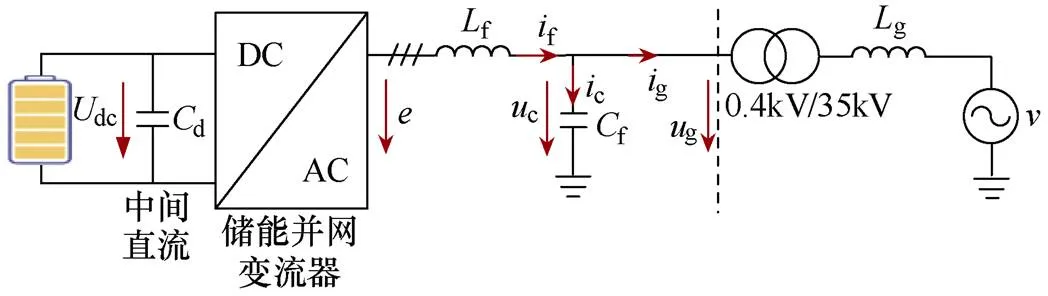
图1 构网型储能并网系统

图1中，储能并网变流器采用GFM控制，其控制框图如图2所示，主要包含功率同步环、交流电压环、电流环和PWM调制环。当储能运行于放电模式时，直流侧电压由前级Buck-Boost变换器控制，后级采用定功率控制。当储能运行于充电模式时，直流侧电压由DC-AC变换器通过直接功率进行控制。交流电压环用以确保并网点电压幅值恒定。

图2中，dcref和dc分别为直流侧电压参考值和实际值；g为公共连接点交流电压，其在dq坐标系的d轴、q轴分量分别为gd和gq；g、f分别为网侧电流、变流器侧电流，它们在dq坐标系下的d轴、q轴分量分别为gd、gq和fd、fq；为DC-AC变流器输出端口电压，其在dq坐标系下的d轴、q轴分量为d和q；ref和分别为有功功率参考值和实际值；为无功功率实际值；为功率同步环输出相位；LPF为低通滤波器，PI为比例积分控制器。此外，GFM储能并网系统参数见表1。

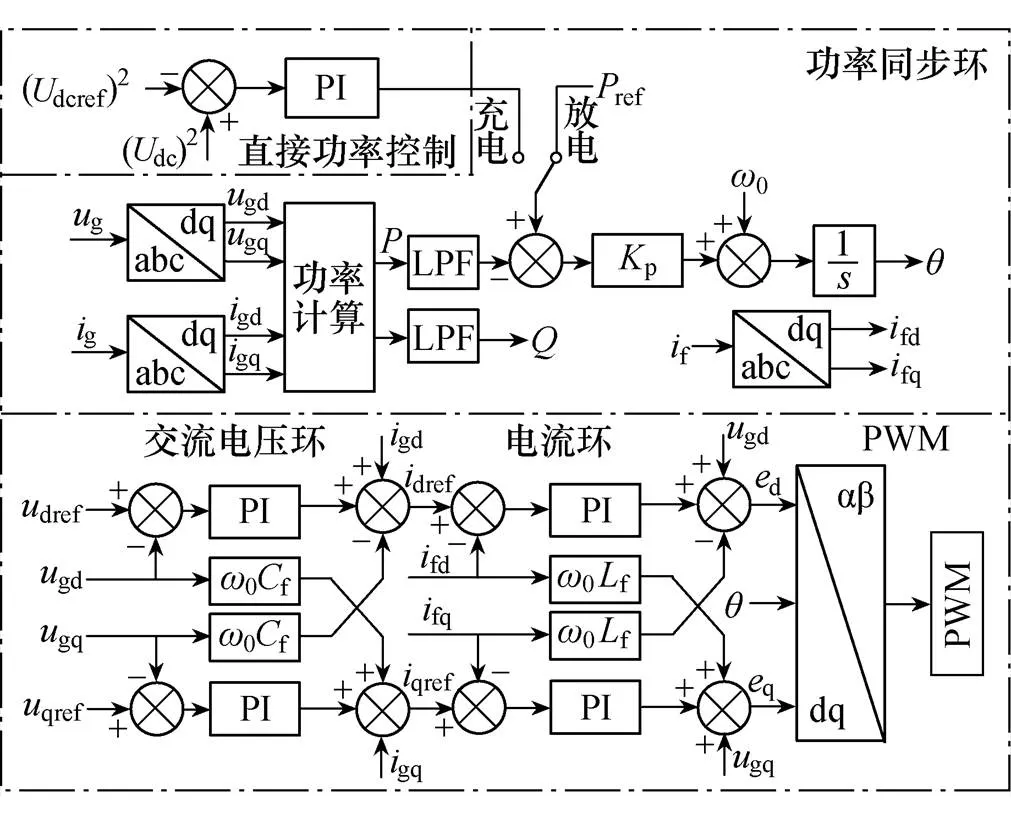
图2 GFM储能变流器控制框图

表1 GFM储能并网系统参数

2 GFM储能变流器并网系统SISO环路增益模型

2.1 功率同步环建模

假定功率同步获得的相位与实际并网点处的相位差为Dq。由实际并网电压相位进行dq变换后的dq坐标系记为系统dq坐标系，在后文的叙述中用上标s表示；利用功率同步环捕获相位进行dq变换后的dq坐标系记为控制dq坐标系，在后文用上标c表示。在GFM储能变流器中的功率同步环节输出相位与实际相位的误差Dq可以表示为

式中：LPF()为功率同步环中的低通滤波器传递函数；D为线性化后的有功功率小扰动量。

不同坐标系下的电压、电流的关系为

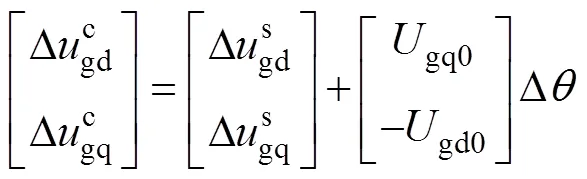
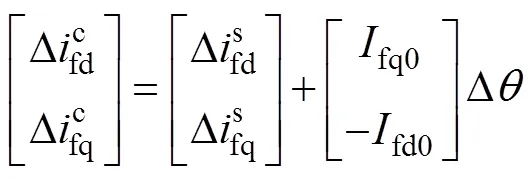
式中：gd0和gq0为公共连接点电压d轴、q轴的稳态值；gd0和gq0为网侧电流的d轴、q轴稳态值；fd0和fq0为变流器侧电流d轴、q轴的稳态值；d0和q0为变流器端口电压d轴、q轴稳态值。

2.2 交流电压环建模

GFM储能需要对并网点的电压进行控制，交流电压环结构框图如图2所示，其小信号数学模型的表达式为

其中

式中：avc为电压环PI控制器；0为基波角频率。

2.3 电流环与PWM建模

GFM储能变流器电流环采用dq电流解耦控制，内环模型为

其中

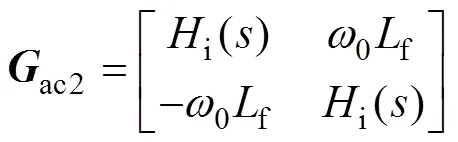
式中，i为电流环PI控制器。

2.4 SISO环路增益建模

根据上述建模可以看出，在dq坐标系下，电压环与电流环的模型均为2阶矩阵，为MIMO系统，而功率同步环的小信号模型则为SISO模型。进一步观察发现，功率同步环的小信号模型的输入为有功偏差，输出为相位偏差。其中，有功偏差为

根据式（8）可以看出，若式中的电压、电流扰动可由相位扰动表示，则联合式（1）即可基于功率同步环构成GFM储能并网系统SISO环路增益模型如图3所示。

由图3可知，建立其SISO环路增益模型的关键在于求取传递函数p。

结合式（2）～式（7），可将所有控制dq坐标系下的电压、电流扰动转化至系统dq坐标系下。进一步基于电路关系，在系统dq坐标系下，网侧电流可以表示为

其中

式中：g、C和L分别为网侧阻抗矩阵、滤波电容导纳矩阵和滤波电感阻抗矩阵；为单位矩阵。

同样依据电路关系，可将网侧电压、变流器端口电压及变流器侧电流均用网侧电流表示，即

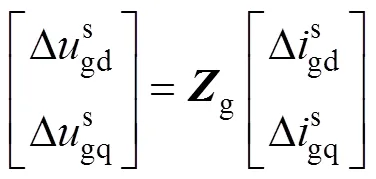
联合式（8）～式（12）可以获得传递函数p，有

其中

综上所述，根据图3，GFM储能并网系统SISO环路增益模型的闭环传递函数为

3 GFM储能变流器并网系统SISO环路增益重塑控制

第2节提出的GFM储能变流器并网系统SISO环路增益模型包含电网侧阻抗参数、储能变流器电路参数及其各个控制环参数。因此，可以利用其开环传递函数，分析不同参数对系统幅值、相位裕度的影响规律。本文选取网侧不同电感、电阻，以及功率同步环系数进行稳定性影响规律的分析。

3.1 网侧电感对并网系统稳定裕度的影响规律

保持网侧等效电阻不变，设置网侧等效电感分别为1mH、10mH和20mH，用以模拟不同强度的电网。等效电感越大则代表其电网强度越弱。绘制出不同网侧电感g下GFM储能并网系统稳定裕度如图4所示。图4中，GM为幅值裕度，PM为相位裕度。

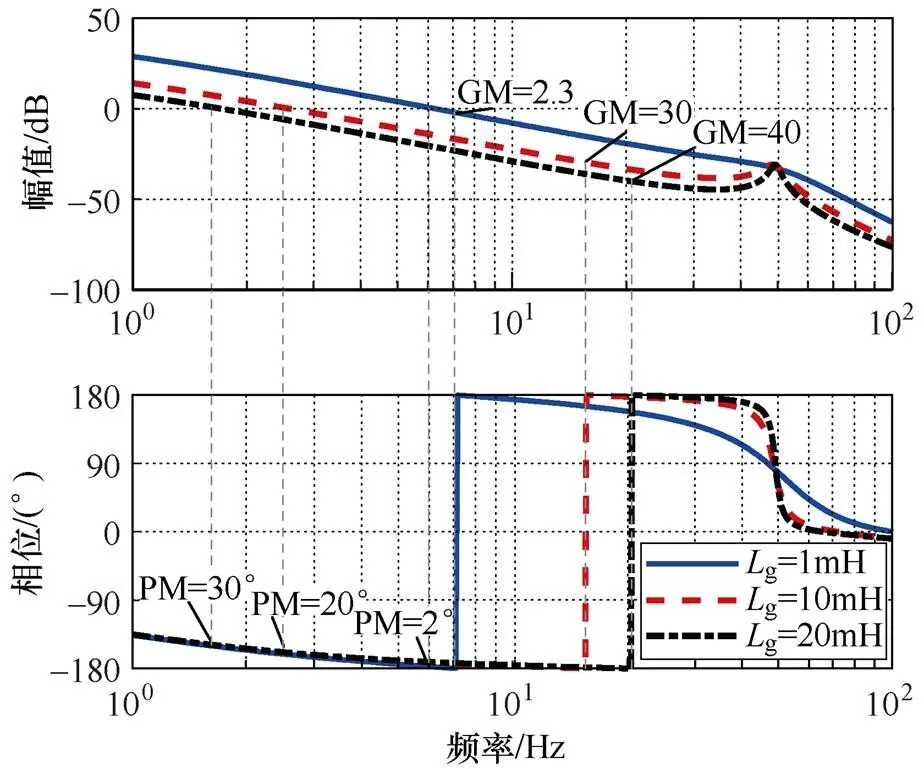
图4 不同网侧电感下GFM储能并网系统稳定裕度

从图4可以看出，随着网侧电感的增加，GFM储能并网系统的幅值和相位裕度均增加，表明GFM储能并网系统在弱电网条件下具有更好的稳定性。当电网侧等效电感为1mH时，虽然系统具有正的幅值裕度，但是其相位裕度接近0°，表明GFM储能并网系统在强电网条件下由于裕度不足，易出现不稳定现象。

3.2 网侧电阻对并网系统稳定裕度的影响规律

在强电网条件下，改变网侧电阻，分别设置0.3W、1W和2W三组参数，绘制不同网侧电阻下GFM储能并网系统稳定裕度如图5所示。

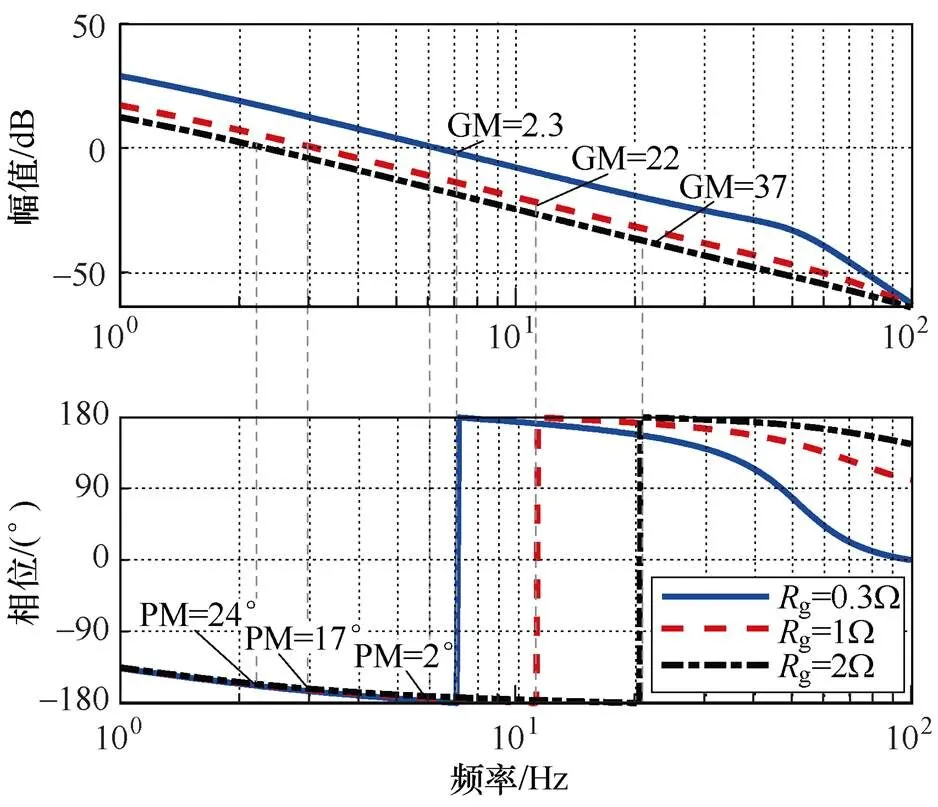
图5 不同网侧电阻下GFM储能并网系统稳定裕度

由图5可以看出，随着网侧电阻的增加，系统的幅值裕度和相位裕度均有所提升，这表明在网侧电感较小的条件下，通过增加网侧电阻可以增强GFM储能并网系统的稳定性。

3.3 功率同步环系数对并网系统稳定裕度的影响规律

由于设计GFM储能变流器电压环、电流环带宽时一般大于功率同步环带宽，因此电压环、电流环控制参数对系统低频段的稳定性影响较小。此处着重讨论不同功率同步环系数对系统稳定裕度的影响。分别在g=10mH和g=1mH的电网电感条件下，使功率同步环系数由0.001变化至0.005，不同功率同步环系数下GFM储能并网系统稳定裕度如图6所示。

图6 不同功率同步环系数下GFM储能并网系统稳定裕度

由图6可以看出，无论是在强电网条件下，还是在弱电网条件下，功率同步环系数的增加都会导致系统的幅值和相位裕度减小。尤其是在强电网条件下，当p=0.001时，GFM储能变流器并网系统的幅值裕度仅有2.3dB，当进一步增加p时，系统的幅值裕度由正变负，将会出现严重的失稳现象。因此，选择较小的功率同步环系数有利于GFM储能变流器并网的稳定性。

3.4 基于网侧电流比例微分反馈的SISO环路增益重塑控制

通过3.1～3.2节的理论分析可以看出，增加网侧电感和电阻均有助于提升GFM储能并网系统在强电网条件下的稳定性。但是在实际系统中，一方面，线路的电阻和电感很难控制；另一方面，增加实际的电阻、电感会增加额外的损耗。因此，可以借鉴虚拟阻抗的思想，通过改变GFM变流器控制环的结构来实现等效的网侧阻抗提升。含虚拟阻抗的GFM储能并网系统如图7所示。

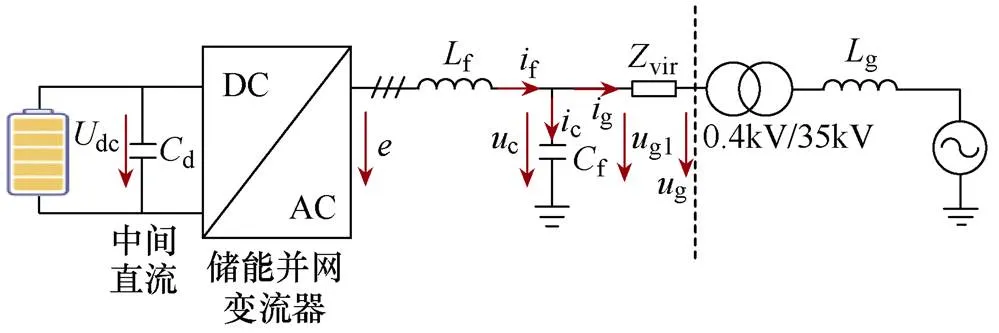
图7 含虚拟阻抗的GFM储能并网系统

从图7可以看出，将GFM变流器中控制电压由原来的g移动至g1后，网侧阻抗可等效为g+vir，从而实现网侧等效阻抗的增加。根据电路关系，可知g与虚拟公共连接点电压g1的关系为

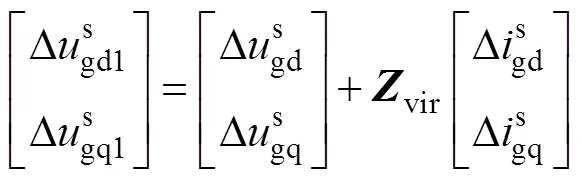
其中

式（15）对应的虚拟阻抗控制框图如图8所示。

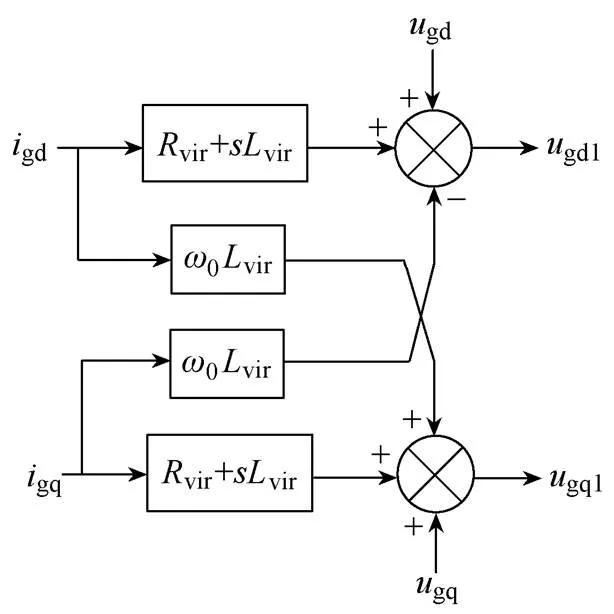
图8 虚拟阻抗控制框图

将图2中的网侧电压信号更换为虚拟阻抗控制的输出电压，即可实现含虚拟阻抗控制的GFM储能变流器控制结构。由图7可以看出，虚拟阻抗的本质是通过引入网侧电流的比例微分反馈，实现控制意义上的“阻抗”特性。因此，通过设置vir与vir即可实现图4和图5中类似的SISO环路增益重塑。

3.5 虚拟阻抗参数对系统的影响

由上述分析可知，增加虚拟电阻和虚拟电感均可有效提升系统的小干扰稳定裕度。从稳定裕度的角度来说，需设置较大的vir和vir。然而，较大的vir和vir也会给系统带来不利影响。

首先，在模拟虚拟电感时需要引入电流的微分反馈，但微分反馈会放大系统的高频噪声。虽然可以通过串联低通滤波器形成不完全微分来减少其负面的影响，但是低通滤波器的惯性会引入控制延时，因此低通滤波器的带宽不能设置得很低，仍然有部分高频噪声会被放大，从而导致控制器无法正常工作。因此，在实际选取时，vir不能太大。

其次，由于虚拟电阻、电感与实际串联接入的阻抗具有等效作用，采用虚拟阻抗控制后会改变系统的稳态运行点，由于网侧电压和输出有功被设置为固定值，虚拟阻抗参数的变化主要影响输出无功电流的大小。根据前文的参数设置，假定实际的网侧阻抗为0，将vir的变化范围设置为0.3～2W，将vir的变化范围设置为1～20mH。在vir和vir构成的参数空间中，绘制GFM变流器稳态无功电流如图9所示。

图9 不同虚拟阻抗参数下GFM变流器稳态无功电流

从图9可以看出，在虚拟电感相同的情况下，增加虚拟电阻会明显增加GFM变流器稳态运行时的无功电流输出，占用储能容量；在虚拟电阻相同的情况下，增加虚拟电感会降低稳态无功电流。因此，从无功电流输出的角度来看，虚拟阻抗参数在配置时应优先选择增加虚拟电感，并辅以较小的虚拟电阻。

综上所述，虚拟阻抗参数在配置时应遵循以下原则：①首先，通过SISO环路增益模型，在给定裕度下给出可行的vir和vir选择方案；②评估控制系统抗噪声能力，确定微分系数vir的上界；③根据无功电流稳态水平确定最大vir所对应的vir。由此，实现虚拟阻抗参数对系统稳定裕度、控制系统抗干扰性能及无功电流稳态水平的平衡。

4 仿真研究

为了证明本文研究的正确性，在Matlab/Simulink中搭建GFM储能变流器并网系统，其参数与表1相同。

4.1 网侧阻抗对系统稳定性的影响

设置g=0.3W，g=10mH为对照组，改变电网电阻和电网电感时，网侧电流波形如图10所示。

图10 不同电网阻抗下网侧电流波形

在1s时，当电网电感由10mH减小至1mH，用以模拟强电网时，从图10（a）可以看出，网侧电流快速发散，最终产生大幅振荡，系统失稳。这与理论分析的减小电网电感会使系统小扰动稳定裕度降低的结论一致；从图10（b）可以看出，当电网电阻由0.3W降低为0.1W时，网侧电流同样失稳，这与基于SISO环路增益模型分析得出的影响规律一致。

4.2 功率同步环系数对系统稳定性的影响

为了研究功率同步环系数对系统稳定性的影响，在g=10mH的工况下，将p从0.001增加至0.005，对应的网侧电流波形如图11所示。可以看出，当p增大后，系统出现发散失稳，这与前文理论分析中p增大会降低系统稳定裕度的结论一致。

图11 不同功率同步环系数下网侧电流波形

4.3 虚拟阻抗控制对系统性能的影响

为了研究虚拟阻抗对系统的影响，引入vir= 0.5W和vir=1mH的虚拟阻抗。在不同电网阻抗下，含虚拟阻抗控制的GFM储能变流器并网系统网侧电流波形如图12所示。

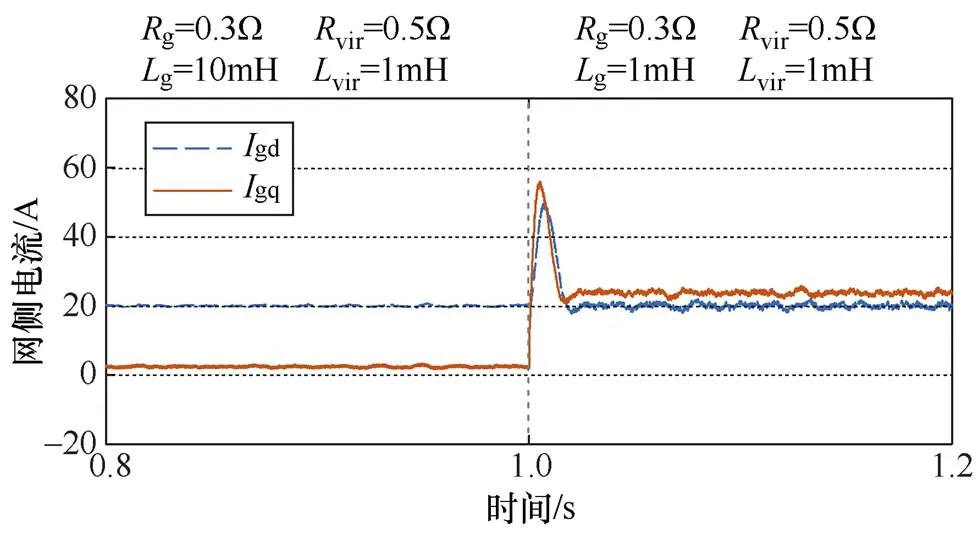
图12 含虚拟阻抗控制的GFM储能变流器并网系统网侧电流波形

由图12可以看出，引入虚拟阻抗控制后，在不同电网阻抗下，系统均能稳定运行。当电网电感由10mH降低至1mH时，无功电流由2.2A增加至23A，实现强电网下公共连接点的电压稳定。

在上述案例的基础上，考虑改变虚拟阻抗参数对系统性能的影响。不同虚拟阻抗参数下GFM储能变流器并网系统网侧电流波形如图13所示。

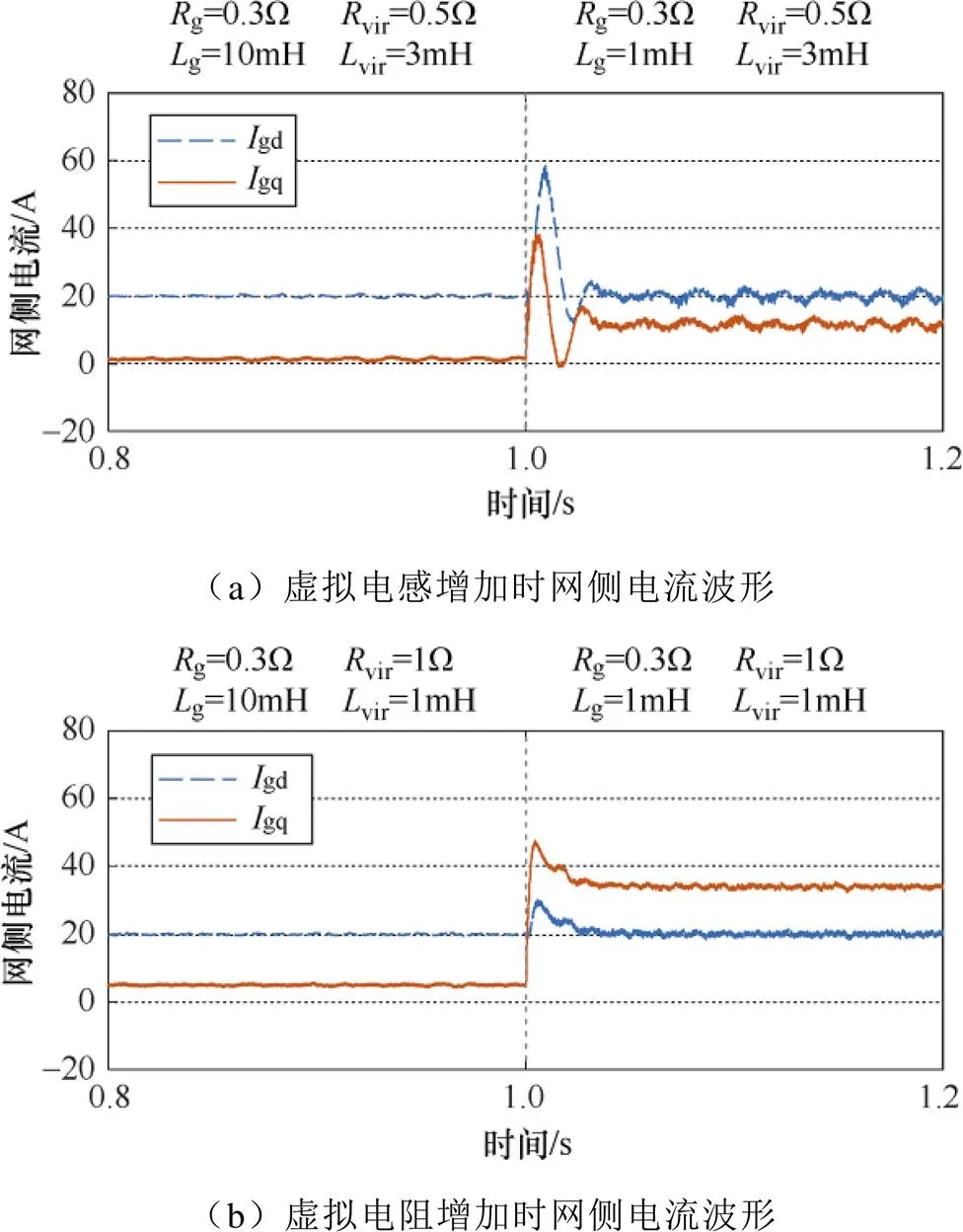
图13 不同虚拟阻抗参数下GFM储能变流器并网系统网侧电流波形

图13（a）中，将虚拟电感增加至3mH，可以看出，在不同电网阻抗下，系统仍可稳定运行。相较于图12所示的网侧电流波形，由于电流微分反馈对噪声的放大作用，导致网侧电流波形的抖动加剧，尤其是在强电网条件下；此外，由于虚拟电感的增加，网侧无功电流的稳态值由23A降低至11A。该仿真结果与第3节的理论分析结果一致。

图13（b）中，将虚拟电阻增加至1W，可以看出，在不同电网阻抗下，系统均可稳定运行。对比图13（b）和图12，可以看出，虚拟电阻增加后，稳态无功电流由23A增加至33A，与前文的理论分析一致。

5 结论

本文建立了GFM储能变流器并网系统SISO环路增益模型，实现了电网阻抗对系统稳定裕度的量化分析，并在此基础上提出了一种基于虚拟阻抗的环路增益重塑控制策略，给出了虚拟阻抗参数的整定方法，得到结论如下：

1）本文所提的GFM储能变流器并网系统SISO环路增益模型可实现系统幅值、相位稳定裕度的量化分析，结果表明，GFM储能变流器在弱电网条件下具有更高的小干扰稳定裕度，而在强电网条件下易出现失稳现象。

2）采用基于网侧电流比例微分反馈的虚拟阻抗控制策略可增强GFM储能变流器在强电网下的适应能力。虚拟电阻、电感参数的选取可参考以下原则：在保证系统具有足够稳定裕度的前提下，选择较小的虚拟电阻；在保证系统具有一定的抗噪声能力的前提下，选择较大的虚拟电抗。这种选取方法可以在保证系统稳定的条件下，尽量减小GFM无功电流输出值，减小储能系统容量的占用率，增加储能系统有功出力的空间。

此外，考虑稳定裕度、抗噪声能力、最小无功电流输出等多目标约束下的GFM储能变流器自适应虚拟阻抗控制方法将是下一步研究的重点。

[1] 丁俊, 王欣怡, 邵烨楠, 等. 新型电力系统的影响因素分析[J]. 电气技术, 2022, 23(7): 42-45.

[2] 谢小荣, 马宁嘉, 刘威, 等. 新型电力系统中储能应用功能的综述与展望[J]. 中国电机工程学报, 2023, 43(1): 158-169.

[3] 安冬, 魏蔓. 抽水蓄能电站励磁系统水泵工况并网流程分析[J]. 电气技术, 2020, 21(11): 110-113.

[4] 张玮亚, 王紫钰, 汤文杰, 等. 飞轮储能系统双向准谐振软开关DC-DC变换器的研究[J]. 电气技术, 2016, 17(12): 20-24.

[5] SALEEM K, ALI Z, MEHRAN K. A single-phase synchronization technique for grid-connected energy storage system under faulty grid conditions[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 12019-12032.

[6] 许诘翊, 刘威, 刘树, 等. 电力系统变流器构网控制技术的现状与发展趋势[J]. 电网技术, 2022, 46(9): 3586-3594.

[7] WEN Bo, BOROYEVICH D, BURGOS R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.

[8] LU Minghui. Virtual oscillator grid-forming inverters: state of the art, modeling, and stability[J]. IEEE Transactions on Power Electronics, 2022, 37(10): 11579-11591.

[9] CHAUHAN P J, REDDY B D, BHANDARI S, et al. Battery energy storage for seamless transitions of wind generator in standalone microgrid[J]. IEEE Transa- ctions on Industry Applications, 2019, 55(1): 69-77.

[10] LI Gaoxiang, CHEN Yandong, LUO An, et al. An enhancing grid stiffness control strategy of STATCOM/ BESS for damping sub-synchronous resonance in wind farm connected to weak grid[J]. IEEE Transactions on Industrial Informatics, 2020, 16(9): 5835-5845.

[11] HUANG Liang, WU Chao, ZHOU Dao, et al. A simplified SISO small-signal model for snalyzing instability mechanism of grid-forming inverter under stronger grid[C]//2021 IEEE 22nd Workshop on Con- trol and Modelling of Power Electronics, Cartagena, Colombia, 2021.

[12] HARNEFORS L, SCHWEIZER M, KUKKOLA J, et al. Generic PLL-based grid-forming control[J]. IEEETransactions on Power Electronics, 2022, 37(2): 1201- 1204.

[13] LIMA L A M, WATANABE E H. Hybrid control scheme for VSC presenting both grid-forming and grid- following capabilities[J]. IEEE Transactions on Power Delivery, 2022, 37(6): 4570-4581.

[14] HUANG Linbin, XIN Huanhai, DöRFLER F.∞- control of grid-connected converters: design, objec- tives and decentralized stability certificates[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 3805-3816.

[15] ME S P, ZABIHI S, BLAABJERG F, et al. Adaptive virtual resistance for postfault oscillation damping in grid-forming inverters[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 3813-3824.

Modeling and reshaping control of single input and single output loop gain of the grid-forming energy storage converter grid-connected system

GUO Xiaolong1YANG Guixing1,2ZHANG Yanjun1ZHOU Yi3

(1. State Grid Xinjiang Electric Power Co., Ltd, Urumqi 830063; 2. School of Electrical Engineering, Xinjiang University, Urumqi 830046; 3. College of Electrical Engineering, Sichuan University, Chengdu 610065)

The energy storage converter is the core equipment in connecting the energy storage system and the grid. However, the interaction between the converter control loops and the grid impedance easily causes small-signal instability of the system. In order to clarify the interaction stability between the grid-forming (GFM) energy storage converter and gird, this paper proposes a power synchronization loop dominated single input and single output (SISO) loop gain model. Based on concepts of traditional magnitude and phase margins in frequency-domain control theory, small-signal stability margins of GFM energy storage converter grid-connected system are quantitatively depicted. The results indicate that the GFM energy storage converter has enough stability margin under the weak grid, but it has insufficient stability margin under the strong grid. Therefore, a loop gain reshaping control based on virtual impedance in the GFM energy storage converter is proposed. Impacts of parameters in virtual impedance control on noise immunity, steady-state operation point and stability of the system are studied for tuning these parameters. Finally, the correctness and effectiveness of the theoretical analysis are verified by the simulation model in Matlab/Simulink.

grid-forming converter; energy storage; small-signal stability; virtual impedance

国家电网新疆电力有限公司科技项目（SGXJ0000TKJS2200419）

2022-10-26

2022-12-03

郭小龙（1983—），男，博士，正高级工程师，主要研究方向为电力系统及其自动化。