辐流式二沉池的流场仿真及评价指标的构建

蒋竹荷,蒋剑虹*,樊 佳,陶 霞,唐清畅,姚 望

(1.中机国际工程设计研究院有限责任公司,中国 长沙 410007;2.湖南省水处理过程与装备工程技术研究中心,中国 长沙 410007;3.长沙市水处理过程与装备技术创新中心,中国 长沙 410007;4.湖南大学环境科学与工程学院,中国 长沙 410082)

在城镇污水处理过程中,二沉池设置于曝气池之后,是活性污泥法处理系统重要组成部分。其沉淀效果直接影响出水水质和回流污泥浓度。与其它形式沉淀池相比,周边进水周边出水辐流式二沉池具有水力负荷、固体负荷和回流污泥浓度高等优势[1,2]。但同时,该形式的二沉池运行效果对配水及其导流装置的水力设计敏感度极高[3,4]。若设计不当,则极易出现配水不均,后续引发短流、二次流和异重流等一系列不利的水流流型及流态,导致二沉池容积利用率低,进而引发翻泥、跑泥、出水水质和回流污泥浓度无法达到设计要求。

目前,二沉池的流场特性及其优劣程度主要依靠在投入运行的池体内进行物理实验测量。常用的方法有流速测试法及示踪剂法[5,6]。这些方法均耗时长,且费用昂贵。而使用CFD模型则可以在任意阶段对二沉池进行模拟分析,并依据模拟结果对流场表现进行评估。王乐对二沉池固液分离及其模拟机理进行了研究,通过与实验结果对比,阐述了不同模拟方法对流场结构模拟的影响[7]。Griborio等人利用CFD模型对拟建圆形初沉池做了潜在水力风险点的甄别,并基于此进行了设计优化,解决了配水不均匀及短流等问题[8]。Wilson等人利用经校准的不同尺度的3D-CFD模型,并结合2D-CFD模型对美国某污水处理厂内已建圆形周进周出二沉池进行了配水均匀性、絮凝潜力(G值)及出水SS的评估[9]。朱贻鸣等人则使用CFD模型比较了不同负荷、不同回流比对二沉池内部的流场变化和污泥质量浓度分布的影响,以此计算出该池最佳表面负荷[10]。

目前,针对沉淀池的CFD模拟研究集中在建模方法及理论,或针对某个特定池体的评估及优化,存在实际操作成本高和通用性不强的问题。本研究以湖南某污水厂周进周出辐流式二沉池为研究对象,分别使用VOF两相流和单相流的3D-CFD模型评估其配水均匀性及池内水力条件,并提出一套快速、可靠的CFD模型构建方法及其评估体系,为二沉池设计及运行优化提供科学依据。

1 研究方法

1.1 CFD模型

1.1.1 控制方程 考虑到二沉池水力半径大,且池内流体为非牛顿流体,具有流变特性,使池内流场结构湍流特征明显。因此,选用描述湍流的雷诺斯托克斯方程(Navier-Stokes Equations,N-S方程)作为本次数学建模的控制方程。其在理想流体欧拉方程的基础上,加入了流体粘度这一关键影响因素。

本研究不考虑传热过程,因此,略去了能量守恒方程,并选取描述不可压缩、牛顿型流体的N-S方程来描述流体的流动。

质量守恒:

∇·u=0,

(1)

动量守恒:

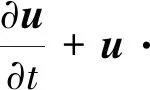
(2)

1.1.2 湍流模型 由于雷诺时均的N-S方程并不封闭,即方程组的未知数大于方程数,因此,需引入湍流模型(即:湍动能方程及湍流耗散率方程)来进行“湍流封闭”。考虑到二沉池中雷诺数变化大、壁面对流体流动影响强,在众多湍流方程中,选取能够描述宽雷诺数范围、同时较为准确描述近、远离壁面的k-ωSST湍流模型[11]。

湍动能方程:

(3)

湍流耗散方程:

(4)

F1=tanh(arg1),

(5)

(6)

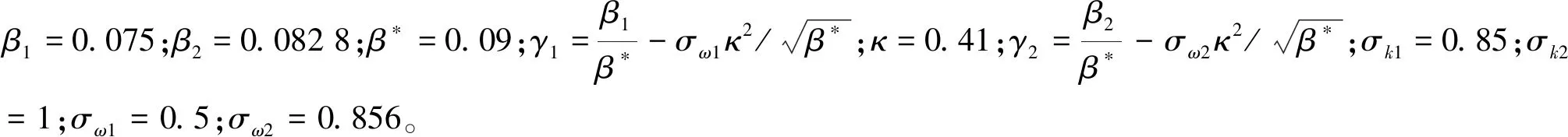
1.1.3 多相流模型 由于本研究目的为评估辐流式二沉池内的流体流型以及水流流速在池体内的分布,不涉及污泥沉降效果,因此无需考虑污泥这一相[7,12]。针对二沉池配水均匀性问题,由于水头损失为影响配水均匀性的重要因素,且自由液面的位置对于明渠流动阻力影响大,因此应在建模时采用VOF模型。而对于池内流场评估,综合考虑计算成本等因素,仅考虑水这一相。

1.1.4 模型几何及网格划分 以湖南省某污水处理厂周进周出辐流式二沉池为研究对象。该池直径30 m,池深5 m,池底坡度为0.01。进水采用牛角型配水廊道,靠近进水口的廊道宽度最宽,远离进口的廊道宽度最窄。59个配水孔均匀分布在配水廊道底部,直径为100 mm。该池的设计规模为1.5×104(m3·d-1),污泥回流比为80 %。水力负荷为1.35 m3/(m2·h),固体负荷为152.78 kg/(m2·h)。本研究分别对现状方案和优化方案建模,两个CFD模型的几何形式见图1和图2。

图1 配水几何模型: (a) 现状方案;(b) 优化方案

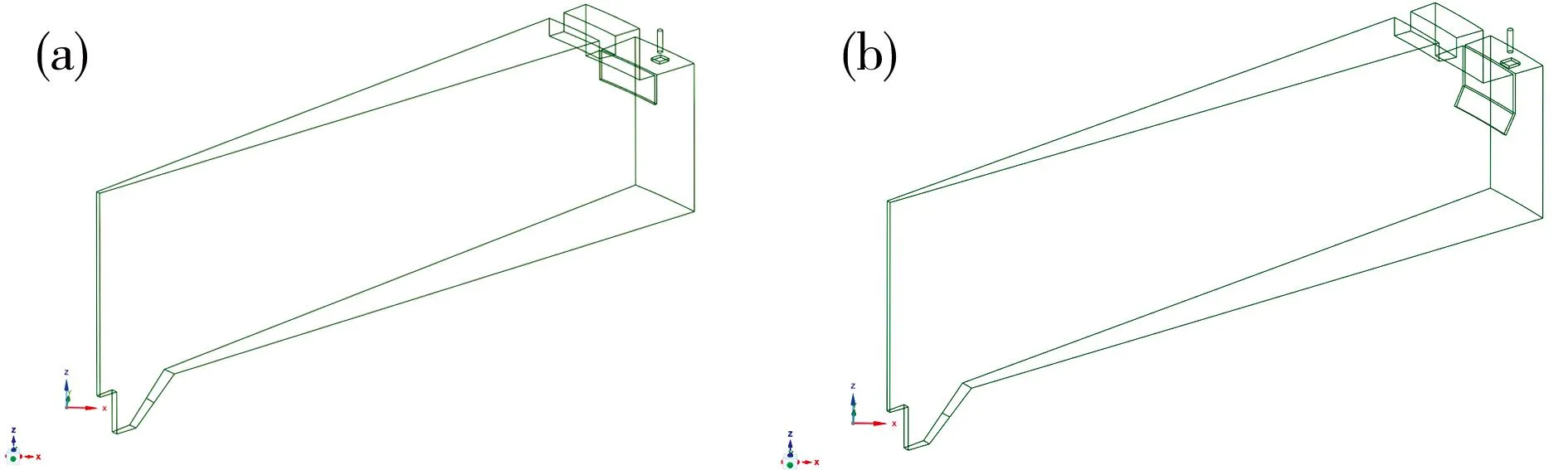
图2 流场几何模型(a) 现状方案;(b) 优化方案

图3 流程池径比示意图

经网格无关性测试,本研究使用的CFD模型网格尺度为0.01 m～0.25 m,网格划分为六面体中心、多面体包围的形式。所有壁面均添加了3层壁面层。最终配水几何模型及流场几何模型的总网格数量分别约为200万个和40万个。

1.1.5 边界条件及数值求解 本研究使用压力基求解,选用有限体积法离散方程,SIMPLEC半隐式算法求解控制方程式。计算求解均选取二阶迎风格式,两模型边界条件如表1所示。

表1 周进周出辐流式二沉池CFD模型模拟的边界条件

1.2 流场评价指标

设计周进周出辐流式二沉池时,选取的水力负荷以及沉淀时间均基于一种理想的水力条件假设。这种假设认为,进水完全均匀地沿池周向池内配水;沿半径方向水流流动性好,无流速极低的区域;且颗粒完全按设计沉淀时间发生沉淀。但在实际运行中,辐流式二沉池普遍存在配水不均、池中心存在清水区、沉淀时间偏低等情况,影响沉淀效果,导致实际运行出水与设计出水偏差较大。因此,有必要针对这3个方面提出评价指标,以科学、定量分析实际与理想水力条件的偏差大小。

1.2.1 配水均匀性 二沉池理想的进水条件为通过每一个配水孔的流量完全相等。此时,过孔流量由下式表达。

q_ideal=Q/n,

(7)

式中,q_ideal是理想配水条件下通过配水孔的流量,m3·s-1;Q是进入沉淀池配水廊道的水流流量,m3·s-1;n是配水孔的数量,个。真实情况下的配水受诸多因素的影响,通过每个孔的水流流量用qi表示。此时,引入过流偏差的概念:

Diff=(qi-q_ideal)/q_ideal×100%,

(8)

式中,Diff表示过流偏差,%。它可用来衡量每个孔真实通过的水流流量与理想流量的差距。该值不宜超出±15 %。若该值在±5 %以内,则认为配水均匀性好[4]。

1.2.2 流程池径比 沉淀池纵断面上理想的水流轨迹应如下图黑色箭头所示。

为量化沉淀池纵剖面上的流程有效长度,本研究提出流程池径比的概念:

旧学院入口处的建筑顶部，有一个巨大的穹顶，穹顶部分是1887年修建的，与原有的院落型建筑完美地结合在一起，可谓画龙点睛的一笔。穹顶上还有一座镀金雕像，名为“青春”，是苏格兰雕塑家约翰·哈奇森的作品。

(9)

式中,F表示流程池径比,%;L1为经配水孔进入池体的水流由池壁流至池中心方向最远处所经过的路程长度,m;L2为水流由池中心向出水堰流去过程中所经过的路程长度,m;D为池体直径,m。

流程池径比可用于评估二沉池整体水力设计的合理程度。F接近100%时,表示进入二沉池的水流流束能够在池体下半部分均匀扩散,沿径向流至池中心,池中心无静滞区(又称死水区)、无短流。F越小,则入流在池内的水力表现越偏离上述情况,池体容积利用率越低。当F小于60%时,认为此时二沉池水力设计不合理,需要重新校核设计参数,如:配水廊道的宽度变化、配水孔直径、配水导流装置及径深比等。

1.2.3 沉淀时间比率 为量化实际停留时间和理论沉淀时间的偏离,本研究提出沉淀时间比率(η)概念,具体为有效沉淀时间与理论沉淀时间的比值:

(10)

(11)

2 模型验证

2.1 实验材料与方法

通过比对模拟结果与文献中的实验结果,测试1.1节中的建模方法是否够准确反映:(1)水流通过孔口引起的水头损失;(2)正常运行的辐流式沉淀池内的流速场。选取Idelchik[13]实验中与本研究配水孔口相同直径孔口在不同流量下的过孔水头损失数据,以验证配水模型的准确性。选取Ramin[14]等在丹麦某污水厂内辐流式二沉池获得的固定半径上的位置、不同水深处水平流速的实验数据,以探究以水为介质的单相流CFD模型与实际运行的二沉池内水平方向流速的差距程度。

2.2 模型验证结果

水流通过孔口产生的水头损失模拟结果见表2,误差控制在10%以内,说明本研究模拟方法可以准确反映水流通过孔口的流动特征,并准确描述由其产生的水头损失。

表2 过孔水头损失模拟验证结果

以距离池中心3 m处为例,该位置不同深度水流在水平方向(即模型中的X方向)速度的模拟值与实测值比对见图4。由图4可知,模型能够准确地描述二沉池纵向上的流速大小及方向的变化趋势,也能准确地描述速度的最大值,最大流速值的模拟误差为1.5%。由图4还可知,模型中流速发生剧烈变化的位置比真实情况偏高,这是由于水比活性污泥混合液比重更低。

图4 Ramin二沉池半径方向3 m处流速随水深的变化模拟与实验值对比

3 结果与讨论

3.1 配水均匀性

为评估现状二沉池的配水均匀性及其优化效果,使用1.2.1节的评估方法对现状及优化后方案模拟结果进行计算整理,结果如图5所示。图中,横坐标由1至59表示沿进水廊道宽度由宽至窄、均匀布置于廊道底部的配水孔口,纵坐标表示各孔口模拟得到的过流流量与理想配水条件下的过流流量的偏差百分比。其中,虚线表示现状方案,实线表示优化方案。

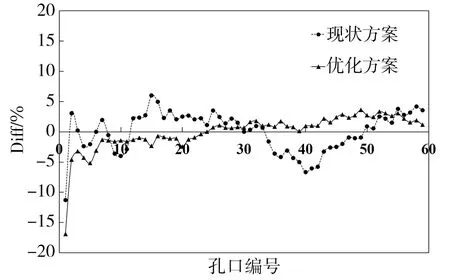
图5 模拟二沉池配水均匀性结果

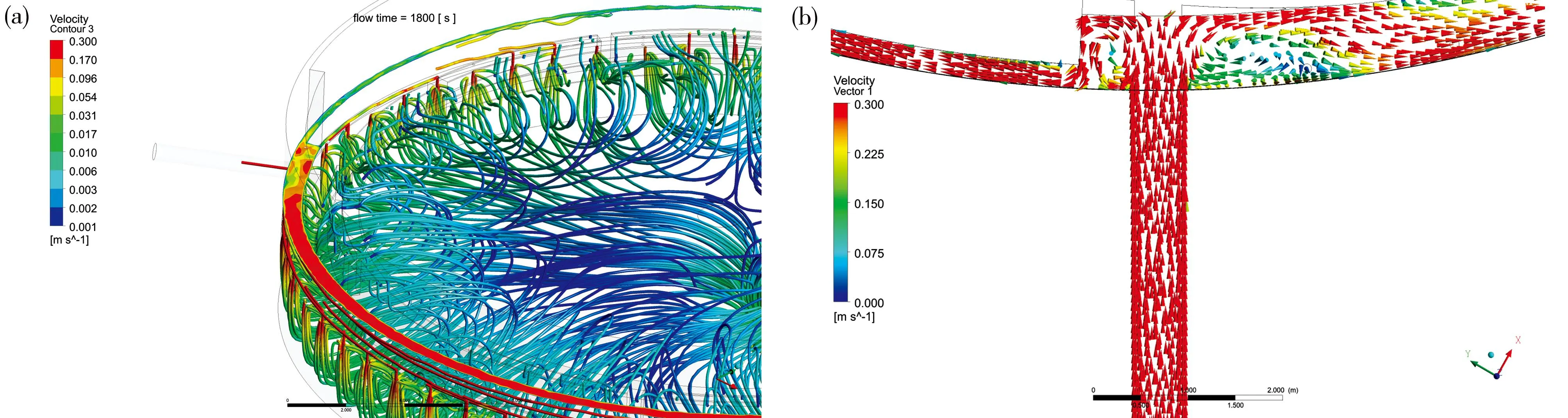
图6 配水模型的模拟结果:(a) 三维流线图叠加自由液面速度云图;(b) 配水廊道中间水深处速度矢量图

为减小配水廊道宽度突然变化引起的配水均匀性波动,优化方案将廊道最宽与最窄处封堵,变为设计中经典的牛角形配水廊道。对于该种形式的配水槽,其设计理念为:(1)廊道内各点处水流流态为缓流,即各点处弗劳德数 (Fr) 小于1;(2)从进水端至配水槽末端,在底部坡度不变的条件下,每个配水孔出流量相等,因此需要廊道内各点水面高度(Hi)保持恒定,进而推得廊道宽度(Bi)需逐步减小。

优化方案的配水均匀性见图5实线。与现状(图中虚线)对比,配水均匀性得到极大提升,认为该形式配水廊道达到设计目标。但值得注意的是,第一个孔口流量比理想值偏低了16.8%,这说明在进水流速较高的情况下,第一个孔口处绝大多数水流撞击廊道壁后反弹向左右扩散。

3.2 流场特征及优化

采用1.1节中所述方法建立的CFD模型对现状二沉池横断面上的流速场做可视化处理,结果如图7 (a) 和(b)所示。由图7 (a)可知,池内有明显伴有旋流作用的辐流流型。结合图7 (b)可看出,水流在池深方向的上部斜向下进入沉淀区,与配水孔正下方处的流速相比较,此处流速未发生明显降低,导致该斜向下流束湍流作用强(不利于沉淀)、触底流速高(极易卷起沉泥);池中心有较大范围的静滞区,说明此处流体难以参与到与周边流体的传质,不利于沉淀;该池有短流,容积利用率不高。

一般认为周进周出式二沉池的流场流态可以通过调整配水系统、池体几何(如:半径、池深)以及底坡等优化[1]。本优化方案主要针对配水廊道下方的配水导流装置。由图7 (c)和 (d)可知,通过调整导流板的形式、位置、方向及尺寸,辐流式沉淀池流场整流效果明显。对比图7 (a)和 (c),整流后的沉淀区流线平顺、整齐,池中绝大部分的辐流流型清晰。对比图7 (b)和(d),整流后经配水孔进入沉淀池的水流在导流板和池壁间充分扩散、消能,进入沉淀区的流速相较于配水孔处流速有明显降低,紊流现象不明显,形成有利于沉淀的水力条件。

3.3 流场优化效果

采用本研究提出的评估指标定量表征优化方案的改进效果,结果见表3。

由表3可以看出,现状方案的流程池径比及沉淀时间比率都不理想,优化配水导流装置后流程池径比提升了35.4%,沉淀时间比率提升了39.0%。研究结果表明,周进周出辐流式二沉池的流场表现对配水导流装置十分敏感,可以通过优化配水,明显提升沉淀池的处理效果。

4 结论

本研究对实际运行中的某厂二沉池进行了CFD模型的构建、验证、模拟及分析。提出了一套适用于评估沉淀效果的水力评价指标,并对现状及优化方案进行了流场评价。结论如下:

1)VOF模型及适应本池几何特征的网格划分策略可以准确模拟明渠内的自由液面位置及过孔流速,可用于评估配水均匀性。经验证,模型的模拟误差在10%之内。

2)以水为流体的单相流CFD模型和湍流模型可以描述二沉池内部流场流态。经验证,模型可反映二沉池半径不同位置处流速随水深变化的趋势,最大流速值的模拟误差在5%之内。

3)研究提出流程池径比、沉淀时间比率可以较客观量化评价不同直径的二沉池的沉淀水力性状,具有较好的实际应用价值。

4) 通过优化现状二沉池配水廊道的几何形状可有效提升二沉池进水的均匀性,有利于提高沉淀池的容积利用率及沉淀效率。配水均匀性可控制在±5%以内。

5) 周进周出辐流式二沉池的流场表现对配水导流装置十分敏感,通过优化配水导流装置可形成有利于沉淀的水力条件。本研究案例优化后二沉池的流程池径比及沉淀时间比率可分别提升35.4%和39.0%。