基于空间管理器和适配器的可重构设备在线放置

彭晶晶，闵阳阳，范 平

(1.湖北科技学院 计算机科学与技术学院，湖北 咸宁 437100；2.内蒙古工业大学 纺织工程系，呼和浩特 010000)

0 引言

处理器(微处理器和数字信号处理器等)是当前大多数高性能计算平台的核心。它们提供了一个灵活的计算平台，能够执行大型类应用程序。微处理器的每个组件的功能是固定的。应用程序是通过解码来自软件的指令流并操作存储在内存层次结构中的数据来执行的。因此，相同固定的硬件可以用于许多通用应用。然而，顺序指令解码和执行、内存访问瓶颈和固定的控制架构限制了所使用处理器所能达到的性能。专用集成电路(AISC,application specific integrated circuits)提供了一种解决通用处理器性能问题的替代方案。ASIC是为专门应用而设计的，因此，每个ASIC对于高度受限的应用程序集都具有固定的功能和优越的性能。然而，大多数应用都有不断更新的算法，需要支持新兴的标准。因此，ASIC限制了架构的灵活性，并限制了任何功能和算法的后期设计优化和升级；采用可重构计算的新计算模式确保了可扩展性和性能之间的权衡。可重构计算利用可以在运行时进行调整的硬件，以促进更大的灵活性，而不影响性能。可重构体系结构由于其适应性，可以利用应用程序中可用的细粒度和粗粒度并行性。与传统微处理器相比，利用这种并行性获得重要的性能优势。硬件的可重构性允许对每个应用程序中的特定计算进行硬件适配，以实现比软件更高的性能。复杂的功能可以映射到架构上，从而实现更高的芯片利用率，减少指令获取和执行瓶颈。

大多数计算任务都具有较高的计算需求和实时吞吐量限制。除了大量的精细计算之外，还有复杂的数据，这些数据在单个应用程序和不同应用程序之间是不同的。一般用途的架构，如微处理器和数字信号处理器，通常不能维持所需的计算和数据流吞吐量。可重构计算正在成为满足应用程序性能和可扩展性同时需求的新范式。与通用体系结构相比，自定义体系结构以匹配应用程序的计算和数据流的能力表明了其优越性。在低级的算法中，有规则的、重复的计算操作于大量具有可预测数据依赖性的数据集上进行。在较高级的算法上，计算具有不规则的依赖性。这些应用特点与可重构架构的优势有重要的关联。

现代可重构设备允许对一部分器件进行重新配置，而其余部分则保持不变，从而在可重构设备的部分空间上分配任务并执行任务。运行时的空间分配(也称为临时放置或在线放置)是可重构计算的核心部分，但目前许多研究都没有专门针对这一目标进行，这在一定程度上是由于可重构设备的制造商通常没有提供无条件部分重新配置功能以及部分重新配置的工具。随着这类设备在市场上的出现，需要对在线放置进行深入的研究。对于在线放置问题，必须解决2个子问题：

子问题1：确定放置由新模块(或新组件，这两个名词表示相同含义，有时也说成任务，文中叙述交替使用这3个说法)实现的新任务的潜在位置集合。

子问题2：按照一组给定的准则选择放置新模块或新组件的最佳位置。

关于在线放置的大多数研究[1-3]都采用空闲空间管理器来解决子问题1，把设备上的空闲空间表示为一组空的矩形。文献[1]研究了一维路由结构和二维路由结构的表示模型，重点研究了针对这两种表示模型的任务调度，并针对可重构系统，提出了硬模块和软模块的在线和离线启发式放置方法。这些方法可以在内部或外部进行，所提出的在线放置算法能比实际中常用的在线放置算法快约15～30倍。对于离线放置，提出了一种基于模拟退火和贪婪方法的放置算法，并表明了其放置要优于在线算法生成的放置，仿真实验验证了算法的性能和运行效率；文献[2]为了提高可重构计算的效率和多任务系统中的在线模块定位，提出了在现场可编程门阵列(FPGA，field-programmable gate array)上的多任务处理方法，即一种新的多阶段任务到可重构硬件映射的方法，并提出了一种新的适配算法作为在线放置的一部分，实验结果表明能够显著减少重新配置的开销；文献[3]提出了一种可重构FPGA在线任务放置的快速最大空矩形(MER, maximal empty rectangle)枚举算法。在每个任务都利用矩形资源的假设下，该算法可以通过MER列表来管理FPGA上的空闲空间。在分配或删除任务时，根据任务及其分配位置选择一系列MER并将其分割成段。通过处理这些段，MER列表可以以较低的内存消耗快速更新。在FPGA上证明了MERS数的上限，分析了算法的时间复杂度和空间复杂度，最后用实验验证了该算法的有效性；文献[4]针对可重构平台上可用系统门数量的增大，以及这些资源的管理和它们在应用程序和用户之间的共享问题，提出了在可重构操作系统中来管理这些资源，给出了操作系统的一组可行组件和一种可行的软件架构，提出了一些性能指标来衡量操作系统实现的质量如区域分割、算法性能和应用性能，最后实现了一个可重构平台上的操作系统；文献[5]针对多任务操作系统的可重构资源管理，提出了一种管理模型和在线调度算法。具体实现是把任务分配给基于块划分的可重构器件。同时在在线调度器和放置器运行2个函数fSPLIT和fSELECT来实现任务在可重构器件上的配置和调度。仿真结果表明，提出的资源管理模型和调度算法不仅能够实现任务集平均响应时间的最小化和有效调度，而且相比于其他调度算法，还能获得更高的资源利用率；文献[6]针对多叉树任务数据流图的划分映射问题，基于粗粒度行并行可重构架构，提出了一种行列剪枝映射算法，分析和比较了二维没有跳变近邻点点互连和行并行互连的可重构单元阵列的映射性能。实验结果表明，该算法可以减少执行时间；对于放入组件，根据放置策略(最佳适配(BF，best fit)、第一适配(FF,first fit)等)[7-9]选择其中一个空矩形，把任务放置在所选择的矩形内，并计算出新的空矩形集合。这种方法(空闲空间分割)的主要缺点是：每当一个新的任务被放置时，空矩形集增加非常快，从而使得寻找一个合适的位置(子问题2)变得困难；此外，到达的任务被作为独立实体处理，因此，通信方面又被忽略了；文献[10]提出了一种任务驱动的嵌入式可重构异构计算平台，通过集群构建的方式，对多个分布式的、承载各种不同异构计算资源的嵌入式计算板卡统一调度管理。利用容器化技术，构建任务驱动的、可重构的任务执行的虚拟计算环境。开发了基于B/S模式的平台可视化用户界面，实现了用户对平台的随遇接入和全网资源可见；文献[11]提出了一种可重构单元的二维任务放置方法。结合包括当前任务与其邻接任务在时间上的重合度，当前任务与其邻接任务的边长的重合度，以及当前任务对其它空闲块的影响程度，依次计算当前任务的长、宽分别沿每个空闲块的每两条相邻边放置时的合适度，选出所有空闲块的所有位置中合适度最大的位置作为当前任务的最终放置位置，可使任务放置更为紧凑合理，减少可重构单元中的碎片，提高可重构单元的空间利用率；文献[12]针对异构系统中可重构计算的任务调度问题进行了研究。通过分析FPGA的硬件结构的主要单元，结合异构系统中可重构计算系统的架构，提出了带有路由资源考虑的FPGA通信架构模型。通过分析现有可重构资源管理策略，提出了基于任务顶点划分矩形的资源管理策略，通过状态矩阵维护跟踪可重构资源的实时信息，并根据任务顶点划分最大空闲矩形；文献[13]提出通过将新到达的硬件任务放置在己布局硬件任务的顶点处，通过对可重构芯片内部计算单元进行编码来迅速判断新任务是否可放置在该顶点。如果硬件任务无法放置，可以通过旋转该硬件任务再进行判断，以提高可重构芯片空间的利用率，并有效地减少布局开销；[14]基于Xilinx设计套件提出了一种放置器架构，适用于异构可重构逻辑体系结构的灵活、快速和无约束的定向放置，特别适合异构FPGA，使得应用程序设计人员能够利用部分动态重新配置的优势，通过动态调度硬件预取来加速应用程序。

基于以上放置策略存在的各种不足，本文提出了一种新的策略在可重构设备上在线放置组件。一方面，利用空矩形集比放置矩形(任务)集增长更快的原理，因而更适合于管理设备上已占用的空间，而不是空闲空间；另一方面，在实际应用中，每个任务都以某种方式与其环境进行通信的，这种通信是以任务的输入到输出的形式进行，因此，任务之间的通信路由在放置策略中起着重要的作用，所以本文在寻找子问题2的解中充分考虑了路由成本的优化。实验结果表明，本文提出的在可重构设备上的在线放置策略，本文提出的空间管理器和适配器相比于目前常用的几种放置方法不仅有更低的复杂度，而且有更低的适配时间。

1 系统模型

在讨论在线放置问题之前，先给出本文要研究的系统模型的相关定义和假设。

假设一个可重构设备R是在一组配置为H行和W列的矩形阵列中的可重构处理元件(PE， processing element)上产生的，这些PE可以某种方式连接在一起。

本文的动态重构模型是在一个调度器、一个在线放置器和一个可重构设备上建立的，如图1所示。调度器管理任务，并决定何时执行任务，然后把任务提交给放置器，放置器尝试将任务放置到设备上，即为该任务分配一组PE。如果放置器不能为新任务找到一个位置，那么该任务将被发送回调度器，调度器可以决定稍后发送它或将另一个任务发送给放置器，在这种情况下，我们说任务被拒绝了。由于本文主要针对系统中的放置器部分进行研究，所以关于调度器的设计不在本文的研究之列。对于要放置到可重构设备上的每个任务来说，我们进一步假设一个矩形模块的实现是可用的，其边界上有输入和输出端口，这个实现存储在一个模块数据库中，并将按需检索。

图1 一种可重构设备的多任务处理系统

我们定义任务特征如下：

定义1 任务特征：给定一组任务T={t1,t2,…,tm}，一个任务tk∈T的特征是4-元组(ak,ek,wk,hk)，其中ak是任务tk的到达时间，ek是任务tk的执行时间，wk是使用PE的任务tk的对应模块的宽度，hk是使用PE的任务tk的对应模块的高度，我们令：

tk=(ak,ek,wk,hk)

(1)

一个任务的到达时间是放置器从调度器接收该任务的时间，它与该任务是否被放置或拒绝无关。在每个时间点，放置器包含一组动态的任务(DST, dynamic set of task)，DST由正在运行的任务和要放置到设备上的新任务构成，PE从DST中动态地插入和移除。

此外，我们还假设任务是不可抢占的(因为配置开销很高,尽管这一假设并不影响放置方法)，运行模块也是不可替换的。由于我们感兴趣的是任务和它们的环境之间的通信，所以不仅要考虑不同任务之间的连接，但要考虑任务和设备边界之间的连接，这对于具有离片通信的任务来说是有用的；对于一个给定的DST，我们定义一组动态连接(DSC,dynamic set of connections)，DSC的一个元素或者是两个任务之间的一个连接，或者是一个任务与边界设备上的一个位置之间的连接。

定义2 任务通信：给定一个DSTT和在可重构设备R边界上的一组位置(引脚,pins)P，我们定义动态通信集为T和(T∪P)之间的边集。

边(p,q)∈C的权值wpq是连接两个元素p∈T和q∈(T∪P)的总线的宽度。

在定义了任务特征、DST和DSC之后，我们在接下来的内容中来阐述本文的在线放置策略是如何实现的。

2 方案实现

2.1 空间管理器

如引言中所述，放置问题的第一部分是确定可以放置新模块/组件的全部可能的位置。

解决这个子问题的最简单的方法是采用Brute Force算法[15-17]。对于要放置的每个新模块/组件c，Brute Force算法通过扫描设备上的所有位置来解决第一个子问题。对于每个位置p=(xp,yp)，算法检查在c和放置模块之间是否会发生重叠，如果组件c要放置在位置p上。

在解决了子问题1之后，通过计算第一步中找到的每个位置的放置成本来计算最佳放置位置，并选择最好的一个作为最优解。

Brute Force算法需要O(H×W×n)的时间来求解子问题1，其中H是可重构设备的高度，W是宽度，n是硬件上运行的任务数。

文献[3,18-19]提出将空闲空间仅存储为最大矩形，这种方法的复杂度是O(n2)。对于大型可重构设备来说，H和W都比n大，因此采用文献[3]的方法要优于Brute Force方法。然而，在文献[3]的方法中，采用二叉树来管理空矩形，这对于通过删除和插入模块来保持更新就非常复杂，因为在某些情况下需要改变树的许多节点。因此，本文提出一种更简单和更快的方法，其复杂度为O(n)。与文献[3]的方法相反，本文提出管理设备占用空间，而不是空闲空间，主要是基于设备上的空矩形集的增长速度比放置组件集要快得多，因此算法将更快地使用已占用的空间来查找可以放置新组件的空闲位置集。

不失一般性，我们考虑组件放置相对于其左下角的位置，首先定义一个新组件的不可能放置区域(IPR，impossible placement region)。

定义1 相对于放置模块的IPR：对于要放置在设备上的一个新组件c和已放置组件c′，c相对于c′的不可能放置区域(IPR)Ic′(c)是不与c′重叠的c不能放置的区域。对于一个已放置组件集C′来说，c的不可能放置区域IC′(c)是不与C′的一个元素重叠的c不能放置的区域，即：

IC′(c)=∪c′∈C′Ic′(c)

(2)

定义2 相对于设备的IPR：相对于设备的不可能放置区域IR(c)是不与该设备的外部区域重叠的c不能放置的区域。

定义3 不可能和可能的放置区域：一个新组件c的IPR是由IC′(c)和IR(c)来确定的，即：

I(c)=IC′(c)∪IR(c)

(3)

通过从设备区域减去运行组件的IPRs和设备的IPRs，就得到c的可能放置区域(PPR,possible placement region)P(c)。如果U是设备上的全部位置集，则有：

P(c)=U-I(c)

(4)

对于一个要放置到设备上的具有高度hc和宽度wc的新组件c以及一个已放置的组件c′，c相对于c′的不可能放置区域(IPR)Ic′(c)是通过计算组件c′的大小为hc-1的左部边缘和大小为wc-1的底部边缘来确定的，如图2所示。

图2 相对于已放置模块的新模块的IPR

通过集成这个边缘和运行任务的区域，就可以得到放置新模块(即由这个运行任务产生的)的不可能区域。然后，确定出全部运行模块的这些边缘，从而得到全部已放置模块产生的不可能区域；此外，可重构设备的边界也有两个边缘，显然，当新模块到达以供放置时，必须重新计算每个已放置模块的边缘。

如前所述，计算出相对于设备和每个已放置组件的IPR，就可以得到IPR集，如图3所示。子问题1的解可以通过从总的设备区域减去IPR集来得到。由于需要计算运行模块的扩展边缘和相对于设备的两个区域来求解子问题1，因此算法需要的计算复杂度是O(n)。

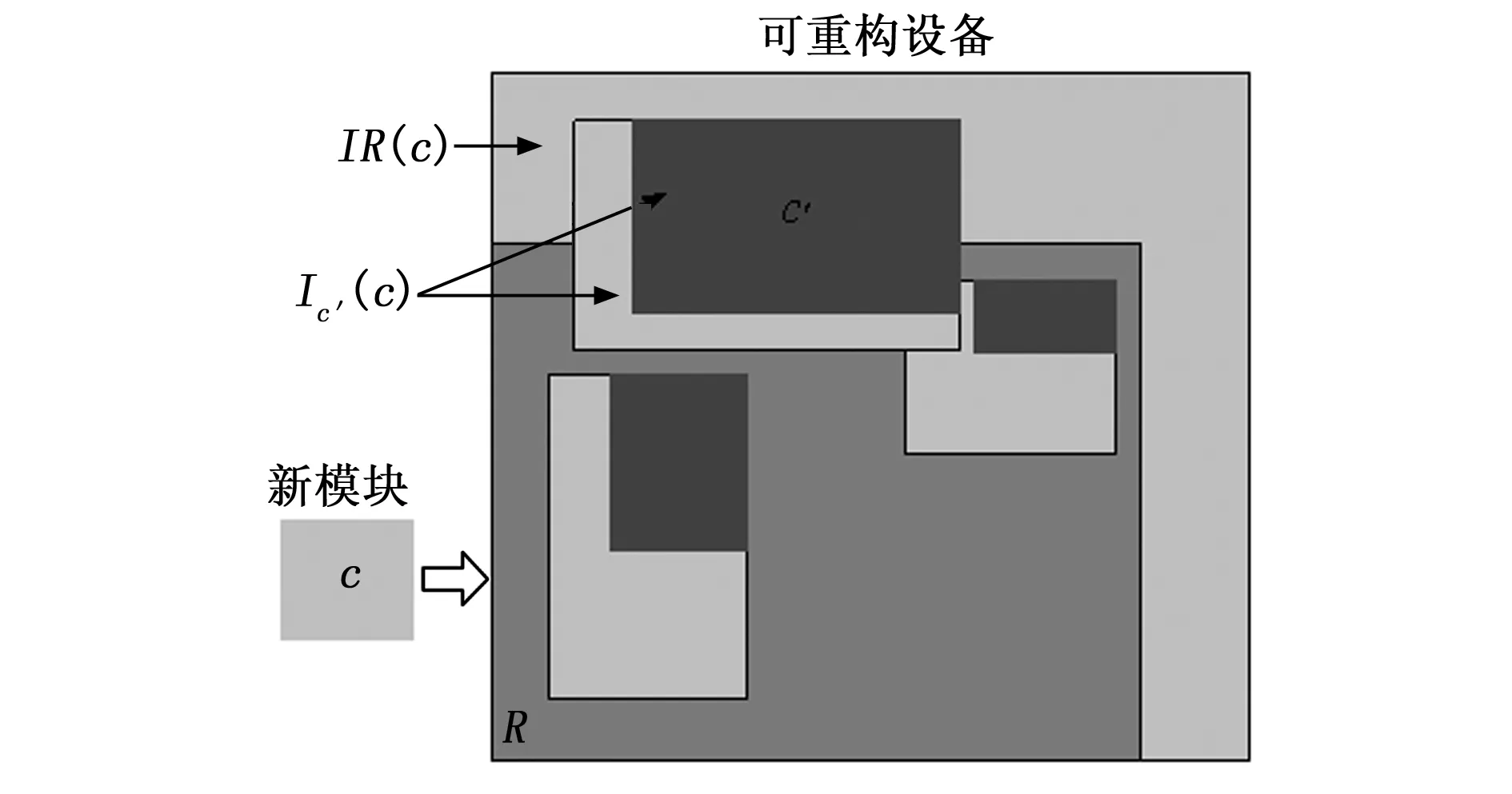
图3 新模块的不可能位置区域

2.2 适配器

在线放置的第二个子问题即子问题2是从可能放置区域集合中找到放置新模块的最佳位置。一种简单的方法[15-16]就是由扫描所有可能的放置位置和计算每个位置的放置成本构成，然后选择最佳的一个位置。这种简单低效的方法需要的复杂度是O(|PPR|*n)，其中n是放置组件的数量，因而Brute Force方法作为一种在线放置算法来说代价太高了。因此，本文首先计算能得到最佳放置成本的点popt，而不是计算出每个点的放置成本，然后选择其中最佳的一个点。如果popt位于PPR内，则就得到了子问题2的解，否则，就寻找最靠近popt的点(popt位于PPR内)，并选择它作为最佳放置位置。

为了确定最佳点，我们首先确定成本函数，这个成本函数应当通过最佳点来使其最小化。最重要的成本函数之一就是路由成本[20]，所以我们的主要目标就是以一种组件之间通信最优的方法来放置组件，这个目标可以通过将连接的组件放置在彼此附近来达到；此外，具有片外/离片连接的组件也应当放置在设备的边界上，而不是远离它们所使用的引脚。

我们定义最小化成本为放置在设备上的组件的通信成本，用距离和总线宽度来衡量，将这种成本称为路由成本，并定义如下：

定义1 路由成本：对于两个模块i和j来说，定义它们之间的路由成本Cost(Rij)如下：

(5)

换句话说，两个模块之间的路由成本就是它们之间的加权距离。为了计算路由成本，我们采用组件的中心点而不是采用左下角点作为参考点，对于模块i，它是由数据对(xi+wi/2,yi+hi/2)定义的，其中(xi,yi)定义i的左下角位置，wi定义i的宽度，hi定义i的高度。如果在两个模块i,j之间没有通信，则wij以及它们之间的路由成本将为零。当我们已有(n-1)个放置模块时，并希望放置第n个模块，那么应当使这个模块对于其他已放置模块的路由成本最小化，根据定义1，得到：

(6)

式中，xn和yn为变量，其他参数是固定的。由于xn和yn是相互独立的，所以式(6)可以写成下列式(7)和式(8)：

(7)

(8)

式(7)的值是xn的函数，则为了最小化，我们必须找到这个函数对xn的偏导数为零的点，即：

(9)

(10)

以同样的方法，可以计算出yn的最佳值为：

(11)

在找到放置新模块的最佳点之后，必须检查该点是否属于PPR集。当该点不在PPR集中时，我们将寻找接近最佳点最近可能位置(NPP, nearest possible position)。如图4所示，在IPR中有4个接近最佳点的点，我们把最接近的一点选择为NPP。如果这一点也是不可行的，则重复前一步，直至找到最近的可行点。图5为覆盖最佳点的不可能区域，以及如何设法确定接近可能的点。

显然，最优化的路由成本会大大降低适配器的适配时间。

图4 接近最佳点的可能点

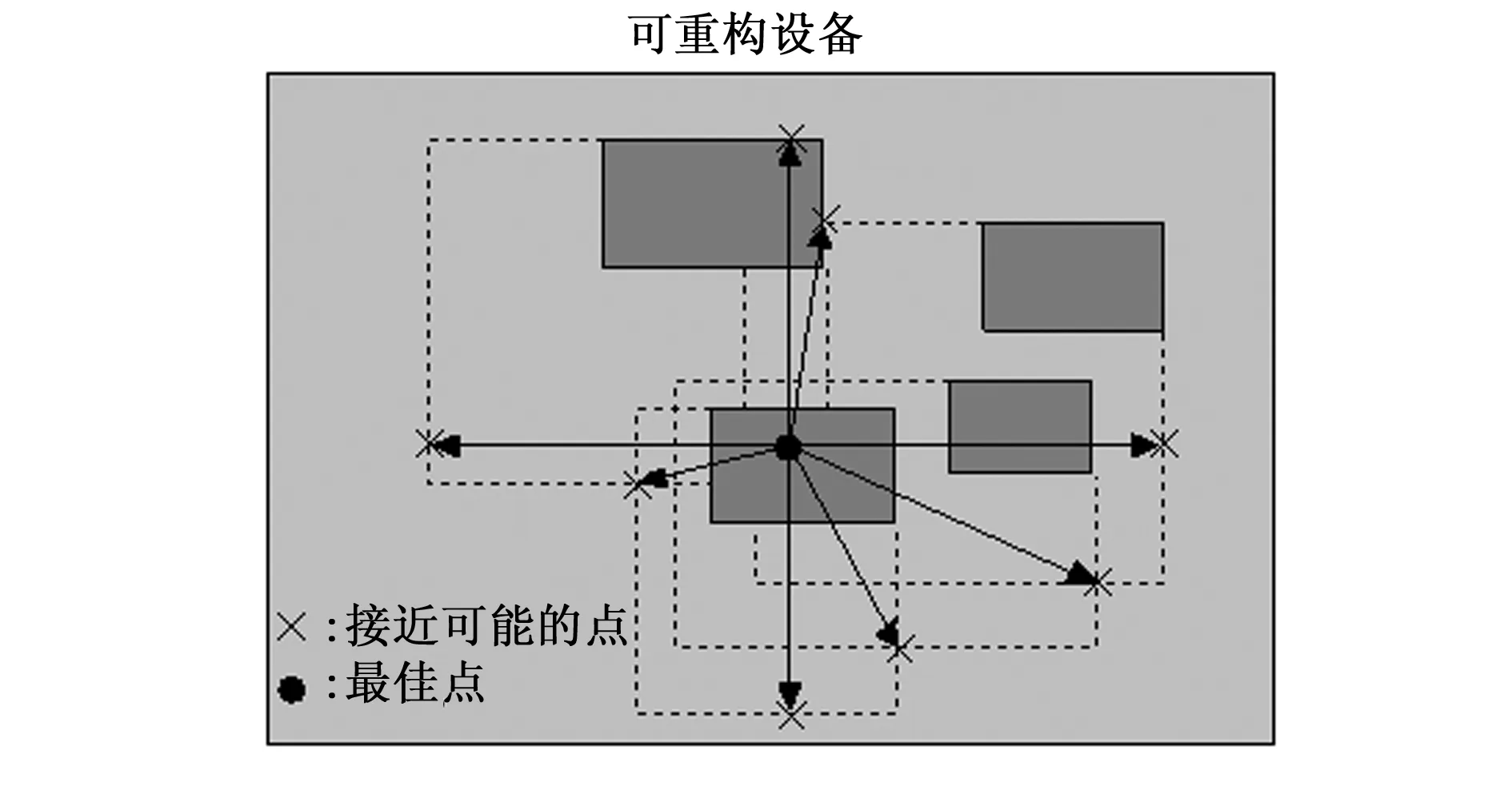
图5 确定接近最佳点的可能点

为了找到NPP，根据每个重叠区域，采用一个接近可能位置的列表。在最坏的情况下，全部不可能区域覆盖这个最佳点，而且列表中的点数目将是O(n)，那么NPP就可以在O(n)时间内计算。 NPP算法的实现步骤伪代码如下：

计算最佳点(新组件)：

if 最佳点是可用的 then

把新组件放置在这个最佳点上

从表6可以看出，2012—2016年青岛市总的就业人数不断增加。2012—2016年青岛市第一产业的就业比重呈现逐年递减趋势，但趋势比较平缓；第二产业的就业人员比重同样呈现逐年递减趋势，其中2013—2014年就业人员比重减少最多；第三产业的就业人员比重在逐年递增，尤其2014年第三产业就业人员的比重增加最大，这是第二产业就业人员大量向第三产业转移的结果。通过分析三次产业就业结构可以看出，2012年青岛市的工业化发展水平属于工业化后期，2013—2016年属于工业化中期。

else

计算NPP:

1.找出所选点所在的边缘外的4个接近点

2.插入这些点到最佳点列表中

3.从接近点列表中选择最接近最佳点的点

4.if 选择的点是可用的 then

把新组件放置在这个最佳点上

else

从接近点列表中删除它,并重复NPP计算步骤

2.3 数据结构

为了实现本文提出的在线放置算法，首先使用一个大小为O(n)的链表(n为运行任务数)来存储在可重构设备上要放置的和正在运行的模块。

算法使用的第二个数据结构是具有与可重构设备尺寸相同的二维矩阵，它代表设备的总状态，因此它的每个元素都给出了一个PE的状态，这意味着当一个点(PE)被一个模块占用时，矩阵中对应的元素将有一个指向相关模块的指针，否则，矩阵中的点指示点为空；此外，为了识别PPR，将在此矩阵上应用扩展和删除边缘的效果。采用矩阵可以访问每个元素并仅在1个计算步骤中获得其状态。另一种需要较少内存的替代数据结构是使用链表，但在这种情况下，必须解析运行模块列表来获取每个元素的状态，其复杂度在每一步是O(n)。正如前面提到的，这里使用矩阵，因此计算速度更快；

算法实现的第三个数据结构是一个动态二维矩阵，它表示每对运行模块之间的通信带宽，其维度大小与运行的任务数相同。该通信矩阵用于选择放置一个新模块的最佳位置，因为需要通信宽度来计算并使放置新模块的路由成本最小化。为了找到放置一个新模块的最佳或接近最佳的点，使用一个链表来保存接近最佳的点，我们总是从这个列表中选择最接近最佳点的点，而且将在上述矩阵中检查这个点，看该点是否是可用的位置，如果是，那么就得到NPP，否则这一点就被一个运行模块或它的边缘所占用；然后，从运行模块的每个边界插入最接近的点到这个列表，并将所选择的点移除；同样在这个列表中，将搜索的踪迹存储起来，因为为了确保不选择运行模块中的一个接近点(它已经覆盖了先前的一个选择的接近点)。如前所述，在最坏的情况下，我们将在这个列表中得到3n个接近的点，因此计算NPP的复杂度是O(n)。

3 方案性能评价

正如前面所讨论的，本文所提出的空间管理器的复杂度是O(n)，而文献[15-16]和文献[3,17]的放置方法的复杂度分别是O(H×W×n)和O(n2)，因此本文提出的空间管理器比一般的空间管理器更优更快。

为了比较采用不同适配方法的性能，把本文提出的适配器即最近可能位置(NPP,nearest possible position)与最佳适配(BF，best fit)和第一是配(FF,first fit)两种策略[7-8]进行比较，比较指标是不同适配方法的适配时间。对此，芯片的尺寸分别设定为56×84(mm2)和80×120(mm2)的二维PE阵列，分别类似于Xilinx Virtex XCV 800和 XCV2000E FPGA设备，针对不同的任务大小和形状，实现一个具有随机生成任务集的系统模型，这对于宽度和高度在不同间隔内均匀分布的任务是精确的。得到的对于具有不同任务大小即[20,40]和[20,30]时的运行结果，分别如图6和图7所示，也得到了近似方形的任务即[28,30]范围的运行结果，如图8所示。

图6 任务大小为[20,40]时不同适配方法的适配时间

图7 任务大小为[20,30]时不同适配方法的适配时间

图8 任务大小为[28,30]时不同适配方法的适配时间

从图6、图7和图8可见，本文提出的适配器在不同大小和形状的任务下都得到了最小的路由成本，从而有最小的适配时间，而BF适配方法得到了最大的路由成本即最大的适配时间；还可看到，在近似正方形任务的情况下，FF适配方法可以得到与本文方法相近的结果，但在全部情况下都比本文提出的适配器方法需要更多的适配时间；另一方面，FF适配方法在路由成本方面比BF适配方法要优。而且当采用更大的芯片尺寸时，本文提出的适配器比FF和BF表现更好，因为它有更多的空间来找到最佳位置。

4 结束语

可重构计算是一种新的模式，与传统计算相比，它具有更高的性能和更高的可扩展性。许多应用程序具有与可重构计算的优势相匹配的计算特征。本文对可重构计算的不同方面作了介绍，概述了可重构计算的显著特征及其分类和体系结构；重点讨论了在可重构设备上的在线放置技术，提出了一种新的空间管理器和适配器用于在线放置。与其他在线放置方案相比，本文所提出的空间管理器保存已占用空间的信息，而不是空闲/自由空间的信息，具有更低的复杂度；同时还考虑了适配器中任务的路由成本，从而得到更低的适配时间；最后采用实验评价了本文所提出的适配器算法和现有的适配器算法的比较。

关于未来的研究，我们打算开发一种框架，使得设计人员在临时放置和通信成本的仿真方面能够直接采用有效的模块来实现；此外，还将研究本文的方案在嵌入式系统环境中的实现。