基于时空融合图的共享单车需求预测系统

马云鹤，王玉玫，赵宇帆

(华北计算技术研究所，北京 100083)

关键字：共享单车系统；需求预测；时空融合图；自注意力；图卷积网络

0 引言

随着近年来共享经济的发展，共享单车因其便利和低碳环保的特性被广泛应用于城市公共交通。其能够有力地解决短途出行问题，被誉为解决大众交通中“最后一公里”的好帮手，有效缓解了城市道路交通拥堵问题[1]。

共享单车系统可以分为无桩和有桩两种。在无桩共享单车系统中，共享单车被分散在城市的各个街道，用户可以在运营区域内任意一点借用和归还共享单车。相比之下，有桩系统可以更好地对共享单车进行管理与维护。此外，在包含共享电动单车的有桩系统中，站点可以作为共享电动单车的充电站。因此，有桩共享单车系统一直在市场中占有重要地位[2]。

有桩共享单车系统也有一些缺点，其中最主要的是每个站点的共享单车分布不均衡，进而导致用户可能面临无车可借和无桩可还两个问题。这种共享单车分布不均的问题，主要是由用户出行行为的相似性和集中性导致的[3]。用户通常早上出门上班，这时位于居民区的共享单车需求量大，可能会导致无车可借;相反，位于工作区的共享单车在早上过剩，可能会造成无桩可还。晚上的情况则正好相反。这两种情况都会导致共享单车在城市中不同时间、不同站点的分布不均衡。针对这种分布不均衡的问题，主要通过使用搬运车在站点之间人工搬运的方式解决。同时也需要一个精确的需求预测模型，来解决共享单车的调度问题。

共享单车的需求预测问题是一个典型的时空数据预测问题，其数据分布在连续空间上的固定时间点和空间点，具有时间相关性和空间相关性，以及两个维度耦合在一起的时空动态相关性[4]。因此，挖掘非线性时空数据中复杂的时空特征是处理时空数据预测问题的关键点。

为此，本文提出了一种新的基于时空融合图的注意力网络模型。该模型使用图1所示的时空融合连接方式，将不同时间片的相同车站节点进行连接，形成一张大的时空融合图，在此基础上采用Transformer[5]的网络结构进行预测，并重新实现了其中的基本算子，主要有：为解决时空融合后节点数量倍增导致的计算量平方增长问题，我们将传统的自注意力机制替换为基于概率稀疏[6]的自注意力机制；将全连接层替换为相邻时间片的图卷积层，以增强模型的图结构表达能力；此外，为补充一些外部特征，在位置嵌入(position embedding)部分除传统的相对时间关系嵌入外，还增加了空间位置、天气、绝对时间等特征。

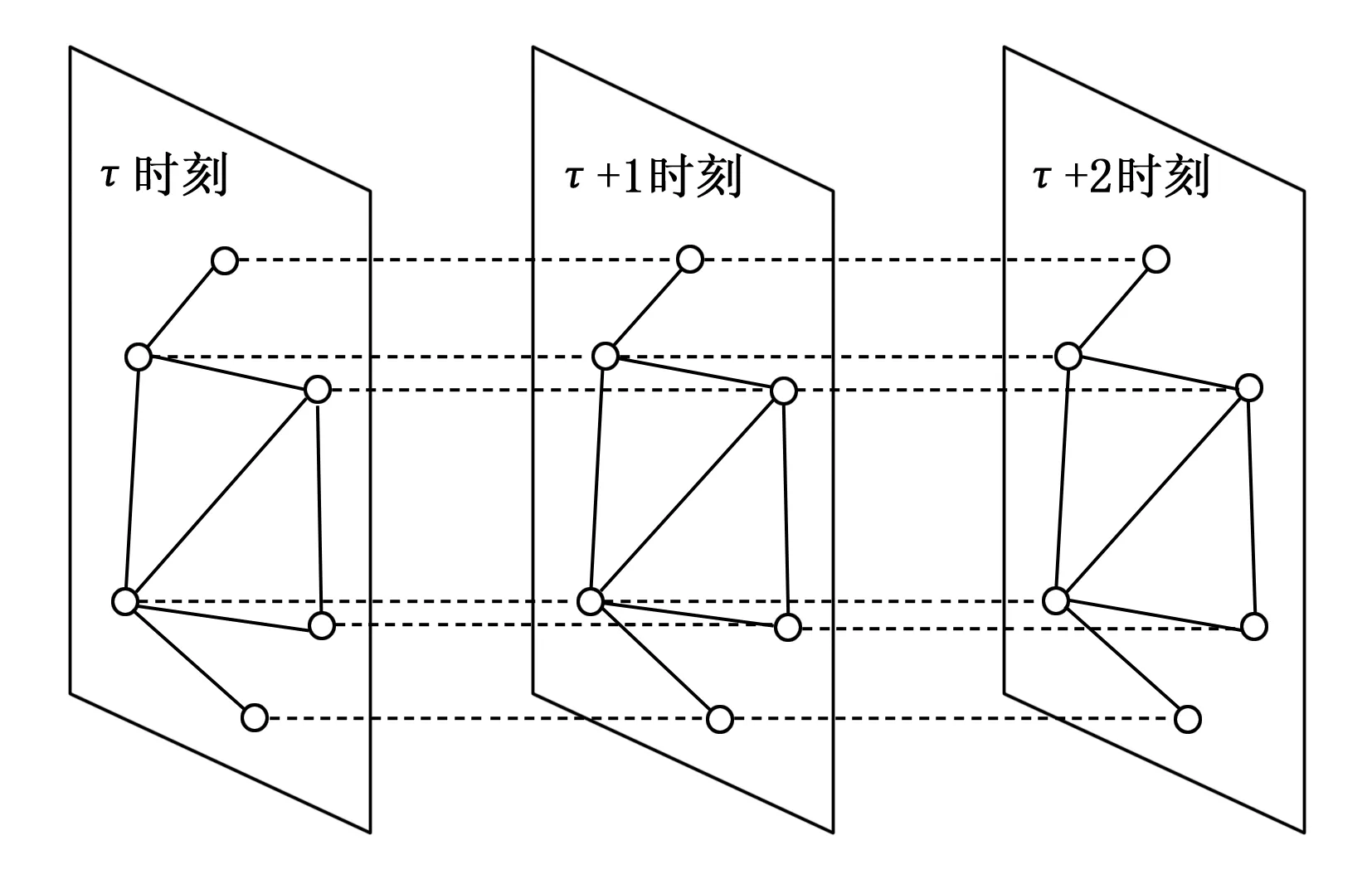
图1 时空融合图

1 共享单车系统时空需求预测概述

1.1 共享单车系统

作为共享经济的重要组成部分，共享单车系统因其低碳、环保、操作方便、健康等优点在全球许多城市得到普及。共享单车系统的发展主要可以分为三代，分别是：1)免费共享单车系统，即早期欧洲的共享单车系统，其特点是小规模、非盈利，主要关注社会和环境问题；2)投币押金式共享单车系统，即对单车增加硬币存取锁装置，共享单车设有固定的存放地点，用户在使用过后也需要在指定区域归还；3)基于“互联网+”的共享单车系统，即以互联网、GPS等技术为基础，由企业运营的线上支付的共享单车系统。

当前对共享单车系统的研究主要从4个方向展开，分别是：系统设计、系统预测、系统操作与系统建议。

系统设计包括站点数量、站点位置、站点容量、站点的共享单车数量等的设计。显然，随着站点数量及其容量的增加，对共享单车重新平衡的需求将减少。然而，这样的增加会给共享单车系统运营商带来成本。因此，在系统设计阶段，需要对成本和需求进行合理的平衡。

系统预测主要包括数据收集以及预测共享单车在空间和时间维度的需求。共享单车的需求预测过程是相当复杂的，涉及用户流动性建模和跨空间和时间域的交通预测。除了正常的时间和空间维度的行为预测之外，还需要对突发的社会事件或交通事故进行及时的反应和预测，这种影响也会在时空维度进行传播。

系统操作指的是为了解决站点内共享单车分布不均的问题，企业需要对共享单车分布失衡的站点内的单车数量进行重新平衡。在再分配过程中，通常使用大型卡车运输共享单车，根据站点内单车的过多和不足情况，在不同的站点存取单车。系统预测的工作可以发现潜在的不平衡，很大程度上决定了再分配的效果。

系统建议是指运营系统可以向用户提出一些出行建议，主要包括两方面，一是附近可以租用或归还的站点信息；二是可以在站点的选择上给出建议，例如当两个共享单车站点对用户来说代价相等时，系统可以建议用户将共享单车归还到共享单车数量较少的站点，以增加整个系统的均衡性，提高长期服务水平。

在以上四个方向当中，系统预测是系统操作和系统建议的前提，是共享单车系统的关键点与难点，也是本文研究的重点。

1.2 时空数据预测

时空数据是对连续空间中多个研究对象的动态变化过程进行采样获得的信息，反映了连续空间中变量随时间的变化趋势。时空数据主要具有以下特点：一是时空动态性，这也是时空预测中最重要的一点。这意味着在预测时空序列时，既要考虑时间维度的依赖性，又要考虑空间维度的依赖性，且随着时间的推进，空间维度的相关性也会动态变化[7]；二是高维性。时空数据除了具有时间和空间两个维度，还有属性维度等多维特征。因此在时空序列的预测中，可以利用时空维度以外的多维属性特征来捕获附加信息，例如天气、是否工作日等；三是海量性，时空序列数据来源广泛、积累时间长，对海量时空序列数据的有效处理是时空序列预测的重要目标。

传统的时间序列预测问题常用的算法有自回归移动平均模型(ARMA，autoregressive moving average model)、自回归综合移动平均模型(ARIMA，autoregressive integrated moving average mode)[8]以及季节性自回归综合移动平均模型(SARIMA，seasonal ARIMA)等。随着机器学习方法的成熟，越来越多的研究者专注于建立基于大量历史数据的非线性时间序列预测模型的研究，经典的模型有基于核方法的支持向量回归(SVR，support vector regression)[9]、随机森林(RF，random forests)[10]和迭代决策树(GBRT，gradient boosting regression tree)[11]等。

近年来，深度学习在很多领域取得了巨大突破，循环神经网络(RNN，recurrent neural network)被广泛用于解决时间序列预测问题。然而对于较长的时间序列，梯度消失等问题限制了RNN的预测精度。为了解决这些问题，研究者提出了长短期记忆网络(LSTM，long short-term memory)[12]及其变体门控循环单元(GRU，gate recurrent unit)[13]，通过在RNN的基础上添加多个阈值门来平衡记忆和遗忘。受到自然语言处理领域中注意力机制的启发，一些研究人员[14]将注意力机制引入基于LSTM的编解码框架，在编码器和解码器之间，采用一个注意力层来转换编码的交通特征，以对过去和未来的时间步骤之间的直接相关性进行建模。

在空间维度上，常使用卷积神经网络(CNN，convolutional neural network)来捕获非线性的空间相关性。ConvLSTM[15]模型是全连接LSTM的一个扩展，它使用CNN和LSTM分别对空间和时间的相关性进行建模。ST-ResNet[16]是一个基于CNN残差网络的城市人流预测模型，其利用深度残差网络在时空网格数据的建模能力来捕获时空相关性。

但CNN只能捕获网格结构数据上各位置的局部空间相关性。近年来，图卷积网络(GCN，graph convolutional network)逐渐兴起，以共享单车站点为代表的典型空间数据源都具有天然的图结构，通过设计基于图的空间数据表示方法，可以提取网格结构无法描述的特征。DCRNN[17]将GCN引入到时空数据预测中，它采用扩散图卷积网络来对空间特征进行提取，采用RNN来提取时间相关性。STGCN[18]在使用图卷积的同时加入了CNN来捕获时间依赖性。ASTGCN[4]在时间和空间两个维度都使用注意机制来捕捉动态的时间相关性和空间相关性。WaveNet[19]设计了一个自适应矩阵，以将节点及其邻居之间的影响变化考虑在内，其使用扩散卷积对时间相关性进行建模，使得感受野指数级增加。

虽然GCN能在一定程度上解决CNN存在的问题，但上述工作都是分别对时间和空间特征进行建模，忽略了时空动态相关性，即，一个区域的交通状态除了与该区域的历史状态相关外，也可能与其他区域的历史状态相关。为此，ST-3DNet[20]将三维卷积引入时空预测领域，可以有效地从空间和时间两个维度混合提取特征，其使用两个组件来分布处理局部时间特征和长期时间特征。STSGCN[21]和STFGNN[22]均使用时空融合图的方式，同时提取时间和空间的动态特征。这种在时空融合图的基础上进行特征提取的方式可以直接捕获时空依赖关系，也是本文中模型的思想来源。

具体到共享单车的需求预测问题，文献[23]以套索回归、岭回归、随机森林和迭代决策树等机器学习模型，探讨了共享单车短期需求预测的主要影响因素，并进行了比较分析。文献[24]提出了新型基于站点聚类的共享单车需求预测算法，通过构建单车转移网络计算站点活跃度，将距离相近和用车模式相似的站点聚合到一个聚簇中，利用多特征LSTM对向量内的特征信息进行学习和训练。文献[25]采用时空图卷积神经网络作为预测模型，在频谱域卷积中使用切比雪夫多项式来降低网络的复杂度，在空间域卷积中以门控图结构作为空间维度的信息传递模型。而在本文中，提出了一种新的基于时空融合图的注意力网络模型，可以更充分的捕获共享单车系统的时空动态相关性，为系统预测提供算法支持。

2 符号与问题定义

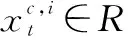
3 基于时空融合图的自注意力网络

本文提出一种基于时空融合图的自注意力网络，以解决共享单车的需求预测问题，整体架构如图2所示。其本质上仍是编解码器架构(Encoder-Decoder)，其中编码器由多个编码层组成，解码器也是由相同层数的解码层组成。Transformer在时间序列预测领域的成功证明了这种网络结构的时间特征提取能力。

图2 基于时空融合图的注意力网络模型

在本文网络模型中，编码层由概率稀疏自注意力和相邻时间片图卷积两个模块组成，其中自注意力模块主要计算每个节点与其他部分节点的相关性；图卷积模块主要为增强模型对复杂过程的表达能力，特别是在图结构下的表达能力。解码层在编码层的两个模块的基础上，增加了概率稀疏跨注意力模块，用来将编码器的信息传递给解码器。此外，在每个模块之后增加了残差连接和层归一化操作。残差连接可以在一定程度上解决网络层数过深带来的梯度消失和权重矩阵退化的问题；层归一化则可以规范优化空间，保证数据特征分布的稳定性，加速模型收敛。

在编解码器之外，我们还将天气特征、空间位置特征、相对时间特征、绝对时间特征等多个外部特征通过嵌入的方式与模型内部的维度统一，并与输入数据相加，以补充输入数据的时空位置信息以及外部特征。模型的输入由τ个时间片内所有节点的全部特征构成，输出为τ+1时刻的空间图结果，然后递归地执行τp次即可得到待预测的全部结果。

3.1 时空融合图的构建

以图3所示的时空图为例，其中存在三种不同的相关性。空间相关性指的是时空图中的每个节点可以直接影响同时刻的邻居节点，这种影响来源于实际的空间依赖关系；同时，由于时间序列中的相关性，每个节点也可以直接影响下一时刻的同位置节点，这表现为时空融合图中的时间相关性。此外，由于某站点的借车数据可以影响到其相邻站点的还车数据，即每个节点可以直接影响下一时刻的邻居节点，故时空图中还存在直接的时空相关性。这三种不同相关性的存在是因为时空图中的信息传播同时在空间和时间两个维度上发生。

图3 时间相关性、空间相关性与时空相关性

由于骑行的空间距离和时间范围的局限性，这些复杂的时空关联通常被局部化，称为局部的时空相关性。此外，由于某一属性的区域内的节点具有一些共性，以及时间的周期性规律，时空数据整体上也表现会出全局的时空相关性，如住宅区上午上班时的借用情况可能与工作区晚上下班时的借用情况类似。

因此，本文通过建立时空融合图的方式对原始数据进行建模，时空融合图把相邻时刻的相同节点进行连接。如图1所示，时空融合图使得原先τ个时间片的包括N个节点的空间图变为一个包含τ×N个节点的时空融合图。图4为时空融合图的邻接矩阵，其中A为空间图的邻接矩阵，I为单位矩阵。在此时空融合图上使用图卷积操作，即可同时提取每个节点的时间和空间两个维度的特征；使用自注意力机制，即可计算任意两个不同时空位置的节点的相关性，这就使得我们的模型具有强大的时空动态特征提取能力。

但与此同时，节点倍增也带来了时间复杂度和空间复杂度的平方级增长，这就需要我们采取一些优化策略，具体而言，我们的模型通过采用概率稀疏注意力机制和相邻时间片的图卷积操作，来降低时空复杂度。

图4 时空融合图的邻接矩阵

3.2 概率稀疏自注意力机制

注意力机制[26]是自然语言处理中基于编解码器的翻译系统的改进，被广泛用于包括计算机视觉、语音处理等其他领域。随着Transformer的提出，自注意力机制逐渐成为了研究热点，其通过计算序列中不同位置的相关性，来提取序列的时间特征。然而，其在计算自注意力时的时间复杂度和空间复杂度均为O(n2)，其中n为节点个数，在处理大量节点问题时具有一定的局限性。

为此，Informer[6]提出了一种新的概率稀疏自注意力机制，其时间和空间复杂度均为O(nlog(n))，以解决长序列时序预测(LSTF，long sequence time-series forecasting)问题。具体而言，在传统的自注意力机制中，每一对输入都会进行注意力的计算，导致在处理长时间序列时计算量过大。研究中发现注意力映射图(attention map)的高激活值较为稀疏，且激活值服从长尾分布(long-term distribution)，即序列中的某个元素一般只会和少数几个元素具有较高的关联性。概率稀疏自注意力的核心思想就是找到这些重要的Q向量，从而只计算这些Q向量的注意力值，来提高计算效率。

LSTF与时空融合图面临的都是大量节点场景，因此，我们在时空融合图上采用概率稀疏自注意力机制，以降低时空节点相关性计算时的复杂度。

3.3 相邻时间片图卷积

GCN可以分为空域和频域两种类型，频域中的一种简化形式[27]为:

(1)

(2)

其中：N(u)为节点u的一阶邻居。

可以看出，对于此GCN而言，某个节点的特征值仅与其一阶邻居有关。因此，在对时空融合图的节点进行一次图卷积操作时，只需要考虑其空间图中的一阶邻居和其前后两个时间点，此时可以捕获图3中的空间相关性和时间相关性；在对时空融合图进行两次图卷积操作时，即可捕获时空相关性。

此外，由于两次图卷积只涉及到二阶邻居节点的消息传递，采用相邻五个时间片的时空融合图的图卷积结果与采用全部时间片的时空图的图卷积结果相同。因此，在实际进行时空融合图卷积时，我们将时空融合图重新划分为多个具有五个时间片的小型时空融合图，在此基础上进行图卷积操作，以进一步降低计算量和内存占用。

3.4 多特征嵌入

自注意力机制只能计算节点之间数据的相关性，而忽略了节点在时空图中的位置相关特征。因此，Transformer中采用位置嵌入的方式，补充提供每个数据的相对时间信息。而在本文中，除了传统的时间特征需要嵌入外，还需要对空间图中的节点位置关系进行嵌入操作，对包括绝对时间特征、天气特征在内的外部特征进行嵌入操作。具体而言如下：

相对时间嵌入采用Transformer中的位置嵌入函数。对于τ时刻的任意节点:

PEpos,2i=sin·(pos/100002i/dmodel)

(3)

PEpos,2i+1=cos·(pos/100002i/dmodel)

(4)

其中:pos为相对时间位置，dmodel为输入到嵌入层的维度，i∈[0,dmodel)表示嵌入层的第i个维度。

空间嵌入即为空间图嵌入，目的是得到网络中节点的低维向量表示。具体而言，对空间图中的每个节点v∈V，计算一个dmodel≪|V|维度的向量。在本文模型中使用Node2vec[28]算法来计算图嵌入，相比于Deepwalk中图的随机游走策略，Node2Vec通过调整随机游走的概率，使得图嵌入的结果在“同质性”和“结构性”中进行权衡。

对于天气与绝对时间特征，采用一个简单的全连接网络，将每个时间点的天气与时间特征计算出一个dmodel维度的向量。

通过对以上多种特征进行融合，得到一个综合嵌入，然后将其与原始数据相加，作为编解码器的输入。

4 实验

4.1 数据集与数据处理

本文使用2019年芝加哥市Divvy共享单车系统数据集(https://divvy-tripdata.s3.amazonaws.com/index.html)，以及对应时间的芝加哥天气数据(https://mesowest.utah.edu/cgi-bin/droman/download_api2.cgi?stn=KMDW)进行实验，使用过去24小时的数据预测未来24小时的数据。数据集按季度分为四组，每组的前60%作为训练集，中间20%作为测试集，最后20%作为验证集。

共享单车站点流量数据每30分钟统计一次，因此每个站点每天包含48组数据，此外，使用滑动窗口的方式生成连续时间序列段。例如Q1共有90天，即4 320个时间点，使用滑动窗口得到4 225个长度为96的连续时间序列段；进一步将前面的2 535个序列段作为训练集，中间845个序列段作为测试集，最后845个序列段作为验证集。

在构建空间图时，如果共享单车站点之间的距离超过10 km[29]，则认为共享单车站点之间不存在连接；反之，则认为存在连接。

Divvy数据集共有691个共享单车站点，我们将其中分布较为集中的137个站点产生的数据集记为Divvy(S)，将完整数据集记为Divvy(L)，以验证本文的模型具有较好的全局时空相关性的捕获能力。

4.2 基准方法与评价指标

在本节中，我们将本文的模型与以下六种现有的时空预测方法进行对比，以验证我们模型的有效性。

SVR[9]：一种监督学习算法，利用线性支持向量机进行回归。

LSTM[12]：RNN的一种变体，用于时间序列预测的长短期记忆网络。

ConvLSTM[15]：全连接LSTM的一个扩展，它使用CNN和LSTM分别对空间和时间的相关性进行建模。

DCRNN[17]：采用扩散图卷积网络和基于seq2seq的GRU对交通图序列数据进行预测。

ASTGCN[4]：通过空间注意机制和时间注意机制来模拟空间和时间的动态相关性。

STSGCN[21]：提出了一种新的卷积运算，可以同时捕获时空相关性。

我们采用平均绝对误差(MAE，mean absolute error)作为模型的损失函数，采用均方误差(RMSE，root mean square error)和MAE作为评价指标，具体公式如下：

(5)

(6)

4.3 实验结果与分析

将我们的模型与以上基准模型在Divvy(S)和Divvy(L)的四组数据集上进行对比，实验结果如表1和表2所示。

表1 不同模型在Divvy(S)上的预测结果对比(Q1-Q4)

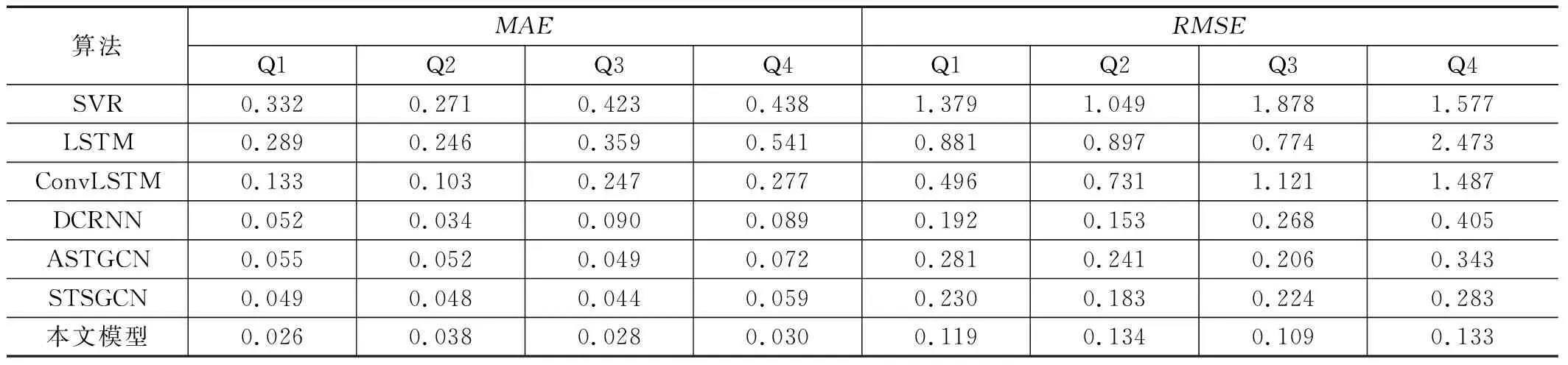
表2 不同模型在Divvy(L)上的预测结果对比(Q1-Q4)

从中可以看出，我们的模型在所有数据集上的两个指标都达到了最佳。其中，适用于时间序列预测的LSTM与SVR由于缺少对空间相关性的捕获能力，结果较差。ConvLSTM是应用于空间网格数据的模型，在输入时将原始数据重构为网格格式的数据；其余模型则是基于空间图数据的模型，采用的是邻接矩阵作为输入。基于网格的模型由于无法捕获图结构中更加丰富的空间信息，其效果差于采用基于图的模型。而在几个基于图的模型之中，DCRNN没有考虑时空中的动态相关性，ASTGCN考虑到了时间动态相关性和空间动态相关性，STSGCN在ASTGCN的基础上，进一步考虑局部时空动态相关性，而我们的模型更进一步，通过在时空融合图上使用自注意力机制，可以捕获全局时空动态相关性，实验结果也验证了我们的特征提取能力。

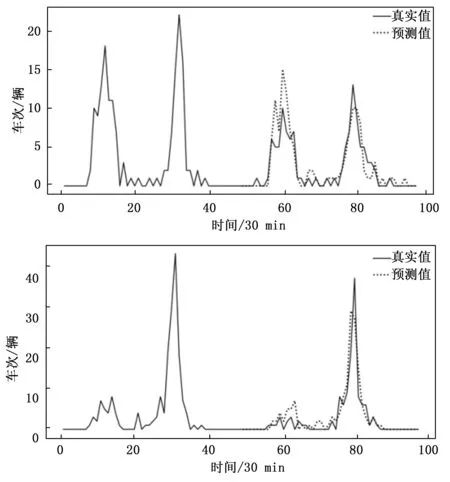
图5 模型在两个测试用例上的预测情况

通过两张表的对比可知，我们的模型在Divvy(L)上较Divvy(S)有最为明显的提升，这是由于区域内节点具有某些共性以及时间的周期性规律，导致时空数据整体上表现出的全局时空相关性。这也显示了在较大空间图上，这种全局时空动态相关性的重要性。

图5为我们的模型在Divvy(L)数据集的第173号站点和482号站点的两个测试用例上的预测情况，从中可以看出，我们的预测结果与真实数据有较强的一致性。

5 结束语

共享单车作为一种新的公共交通形式，极大地丰富了人们的出行方式。然而，在实际应用中，由于用户出行习惯的相似性和集中性，常常会导致各个站点的共享单车分布不均衡，使得用户面临无车可借及无桩可还的问题。为此，本文提出了一种新的基于时空融合图的注意力网络模型，采用Transformer网络结构进行预测，并重新实现了其中的基本算子，以捕获站点之间的时空动态相关性。实验表明，我们的模型在Divvy真实数据集上的表现优于以往的模型。在未来的研究中，我们将对时空融合图进行更细化的设计，考虑时间边和空间边的异质性，更加针对性地设计时空融合图的嵌入方式。