基于超状态隐马尔可夫模型的智能电能表非侵入式故障远程检定

荆臻，王莉，杨梅，王者龙，王晓泳

(1.国网山东省电力公司，济南 250002； 2.山东省计量科学研究院，济南 250000)

0 引 言

电能在输配电过程中每年会产生接近10%的损耗，给电网企业带来巨大经济损失[1-2]。电网系统中的电能损失包括技术性损失(Technical Loss，TL)，即有系统本身导致的不可避免的损失，与非技术性损失(Non-Technical Loss，NTL)，即人为因素造成的损失[3]。其中，引起非技术性损失的一个主要因素是使用了计量误差较大的智能电能表，这可能是由设备自然老化或者对电表的恶意操纵(如窃电行为)引起的[4-5]。除了经济上的损失，智能电能表的计量误差和故障还可能导致电网规划和扩建的决策偏差。而在微电网调度等高实时性要求场景下，电表故障也是重要的安全隐患[6]。随着智能电网系统中新成分的增加和复杂程度不断上升，高效的智能电表故障自动检测和定位具有较高的实际意义。

针对这些问题，基于超状态隐马尔可夫模型(Super-State Hidden Markov Model，SSHMM)提出一种智能电表非侵入式故障远程检定方案，该方法依赖于部署在用户端的智能电能表与一个云数据中心。本文方法不仅能检测智能电能表中的实际故障，还可以预测最有可能出现故障的电能表，从而为电力运营商的进一步决策提供参考。

1 方法原理

对智能电能表的故障检定已经存在大量研究，典型的有聚类[7]，决策树[8]，随机森林[9]，神经网络[10]以及这些方法的组合或集成模型等[11]。这些方法往往都蕴含着可用数据量大的隐含假设，而在真实场景下，由于数据获取困难或数据隐私安全等原因，实际上可用于模型训练的数据量并不总是足够的。并且，对于故障检定这类问题，还存在着样本分布严重不均，即正样本(故障情形)数远低于负样本(正常情形)数的困境[12-13]。基于这些原因，本文设计了一种新的处理手段，将一定区域中央电能表计量(作为总耗电量)与单个智能电能表的读数进行比较。该方法可以在具有较少的电能表计量数据的添加下检测出电能表故障。

1.1 超状态隐马尔可夫模型

超状态隐马尔可夫模型(SSHMM)基于经典的隐马尔可夫模型(HMM)。HMM已在非侵入式负荷监测，电能质量分析等领域得到了较多应用[14-15]。在HMM中，总是假设有一组不可直接观测或测量的状态变量，如图1中的图模型所示。

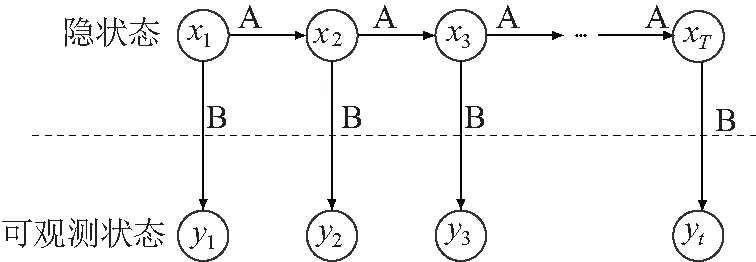
图1 隐马尔可夫模型的概率图表示Fig.1 Probabilistic graphical representation of hidden Markov models

一般的HMM模型形式为：

λ=(X,Y,A,B,p)

(1)

式中X={x1,…,xN}是一组内部状态(隐状态)向量；对应地，Y={y1,…,yN}是一组可观测状态向量；A∈RN×N与B∈RN×M分别为状态转移矩阵(描述N种内部状态中一种状态转化为其他状态的概率)与输出概率矩阵(描述可观测状态的M种不同取值出现的概率)，向量p描述了初始时刻处于各个状态的概率分布[16](图中未绘出)。

在超状态的HMM即SSHMM中，允许将若干个单一状态组合成一个超状态，每个超状态的定义都是明确的，且可以重新分解为构成其的单一状态。在故障检定问题中，可以作这样的定义：X为一组超状态，xi为第i个超状态，Y为一组总用电量向量，yt为t时刻的中央电能表计量值。由于每个超状态代表单个电表计量的一个唯一组合，因此X的维数由每个用户节点馈线的额定供电和所用电能表设备的分辨率决定。

1.2 模型的训练

在使用SSHMM时必须已知初始概率、输出概率和转移概率，这些变量可以通过设备的参数、使用时间等数据来赋予一个预设值，但更合理的做法是从实际数据中估计。首先，通过一定时间内的用电量数据得到一个近似的用电概率质量函数(Probability Mass Function，PMF)，定义为：

(2)

(3)

搜索到最大值后，所有的概率值将进行分箱操作，每个“箱子”中标记了该组的最大概率值。由于最大值一般是非等距分布的，因此每组概率的特征既包括概率之和，也包括了左右边界，即：

(4)

与：

(5)

式中H(n)表示第n个最大值；L(n)和R(n)分别表示其所在组的左右边界，注意位于最左端和最右端的组也被限制在合理范围内。反复按照式(3)与式(4)计算，就可以得到所有组的左右边界位置。

假设设第m个用户所在的“箱子”为K(m)，故超状态k可以由K(m)中的各状态组合得到：

(6)

于是得到了用于故障检定的SSHMM模型：

(7)

式中pt(n)是系统在t时刻处于超状态n的概率；St表示t时刻实际的超状态；A为各超状态之间的转移概率矩阵；矩阵B描述了当观测到yt时系统处于St超状态的概率。

1.3 单个电能表的状态推断

根据1.2中的方法，基于一部分的历史数据便可以估计出SSHMM的转移概率矩阵等参数，此时的“超状态”实际上指大量用户节点处部署的智能电表的工作状态的组合。由于超状态是可分解的，利用Viterbi自适应算法便可以方便地推断出单个电能表的运行状态估计，在云数据中心中实现对智能电能表的非侵入式远程故障检定[18-19]。根据Viterbi算法，基于当前和最后一次测量值，电能表处于超状态i的概率为：

pt-1(i)=B(i,yt-1)pt-2(i)

(8)

实际应用中通常采取一阶马尔可夫假设，因此pt-2(i)可假定为常数，记为p0，从而在t时刻，式(8)可以写成

(9)

采用极大似然估计(Maximum Likelihood Estimation，MLE)，可以取令pt(i)最大的i作为电表在t时刻的超状态。该计算过程的时间复杂度为Ο(c·lgN)，其中c为超状态的数量。

相比传统方法，SSHMM方法的一个显著优势是不要求所有节点都部署智能电表，而是以非侵入的方式实现用电量估计。

2 实验分析

2.1 实验设置

使用了两个公开的数据集：ECO数据集[20]，包含8个月时长内60个家庭的高分辨率智能电能表计量数据，以及REFIT数据集[21]，包含2年内2 000个家庭的电能表计量数据。实验中使用的计量包括有功功率、电流、电压等。所考虑的智能电能表状态在计量上表现为6种类型[22-23]：(1)无异常状态，计量值可视为真实用电量；(2)计量值始终为常数；(3)计量值相对真实用电量以恒定的倍数α放大/缩小；(4)计量值相对真实用电量以非恒定的倍数放大/缩小；(5)计量范围故障，即计量值被限制在某个最大值M以下；(6)计量值存在随机噪声，但相比真实用电量平均下降/上升了β个单位。

两类方法：基于统计的方法与基于模型的方法用于比较本文模型的实际效果。统计方法基于离群点检测，即将超过给定阈值的点判定为异常。阈值通常取平均值偏离k个标准差，在随机选择的3周数据中，ECO数据集上的k值最佳取值为1.65，REFIT数据集的最佳取值为1.30。一般来说，样本所选择的数据时间跨度越大，k值也相应地变大，以适应数据中的固有偏差。

图2显示了ECO数据集中随机抽取的8名用户在20天内平均用电量的偏移情况，k值设置为1.30。图中标出了平均值与被认为是“正常”用户所容许的用电量上下界，因此4号与5号用户的电能表计量被算法判断为异常，其电表存在故障的概率较大。

图2 基于离群点检测的故障电表识别示例Fig.2 An example of novelty discovery based smart meter fault detection

基于统计的方法显然是最直接的一类方法，其缺陷也是显而易见的，即只能检测出使电表计量出现严重偏差的故障，如(3)类故障。而对于更为复杂的(4)类故障，电表的计量值尽管在任意时刻都存在误差，但在总体上统计特征(如均值)依然保持不变，则在图1中将不会表现为离群点。类似地，离群点检测方法对于检测(5)类、(6)类故障通常也是无效的。

基于模型的方法假设了各个用户在长期上看用电量总是在总体上占据稳定的份额，因此可以对于任意用户，可以使用其他用户同期的用电量对该用户的用电量基于一定的模型(如线性模型)进行预测，根据预测值与真实值的偏差判断电能表计量是否存在误差。

2.2 实验结果

评估SSHMM方法的性能需要考虑几个因素的影响，包括：(1)训练数据量，用所覆盖的天数表示；(2)计量数据的分辨率；(3)所使用的电表计量指标；(4)模型的稳定性，表征模型在每次检测任务前都需重新训练的必要性，通过模型在若干天后的数据上性能下降的程度来体现。

在REFIT数据集以1～5周和100天为时间步长分别训练SSHMM模型，并比较模型在故障检测任务上的平均F1值，结果如表1所示。尽管从直观上理解，训练集中的数据量越大，模型的性能应该越好，但由于故障检测问题的特殊性，当数据量较大时，模型在优化时会倾向于“掩盖”异常，即学习到了训练集中与均值偏差较大，但被标记为正常的样本特征，这样反而降低了泛化能力。综合考虑模型泛化效果和复杂程度，本文认为以2周作为训练步长是较合理的方案。

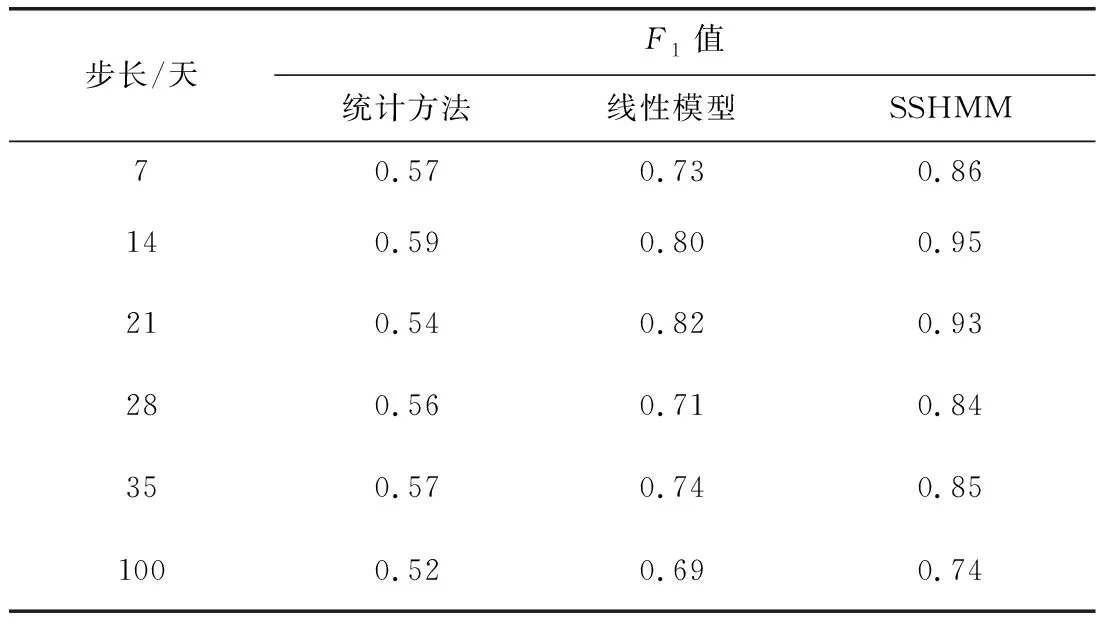
表1 随训练时间步长的模型性能变化Tab.1 Variation of performances of models with time step length of training data

图3给出了步长取14天时SSHMM方法对故障类别划分的混淆矩阵，可以看出，模型在正常电能表与5种故障状态的识别任务上都表现出相当优秀的效果。

图3 SSHMM模型在故障分类任务上的混淆矩阵Fig.3 Confusion matrix of SSHMM model in fault classification task

表2显示了分辨率对于SSHMM模型检测效果的影响(步长取14天)，通过实验发现，15 min为最适宜的分辨率。

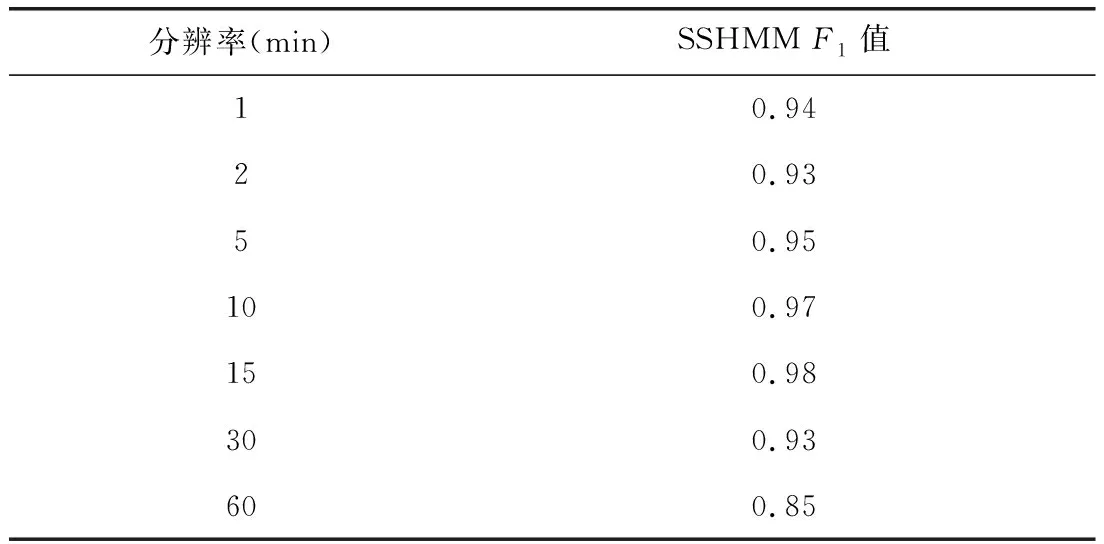
表2 随计量数据分辨率的SSHMM模型检测性能变化Tab.2 Variation of fault classification performances of SSHMM model with temporal measurement resolution

表3给出了以14天步长、15 min分辨率一次训练后的模型对于一段时间后的数据的泛化效果。可以看出，SSHMM方法在训练完成后在100天后的样本上依然具有不错的效果。这说明SSHMM故障电表检测模块可以稳定地部署在云数据中心上，而无需频繁地训练，这无疑是该方法的一大优势。

表3 SSHMM模型在后续数据上的检测性能Tab.3 Performances of SSHMM model on subsequent data in fault classification task

3 结束语

文中介绍了一种超状态隐马尔可夫模型(SSHMM)的智能电能表故障远程检定技术。相比传统方法，SSHMM方法对智能电能表安装量需求更低，并且可以以非侵入的方式实现远程的故障电表识别。实验结果表明，SSHMM方法在检测准确率上可以满足实际需求，且稳定性较高，适合部署在智能电网云平台上，具有一定实际意义。