含风光储联合发电系统的主动配电网无功优化
2023-03-02孙浩锋章健熊壮壮廖晓辉吴龙
孙浩锋,章健,熊壮壮,廖晓辉,吴龙
(1.郑州大学 电气工程学院,郑州 450001; 2.国网山西省电力公司晋城供电公司,山西 晋城 048000)
0 引 言
随着太阳能、风能等分布式能源的发电技术及利用效率的日益提高,分布式电源(Distributed Geneaion,DG)在配电网中渗透率也越来越高。但是太阳能及风能等分布式电源的不确定性会给配电网的电能质量带来诸多影响,如配电网电压产生畸形、造成电网中频率与电压的波动与偏差及短路电流升高等[1]。实际上,不同类型的分布式电源在时间上存在很强的互补性,可以通过互相弥补来解决能源间歇性的缺点,所以若将不同类型的分布式电源联合发电,这样既能相互弥补降低波动性,又能减少其不确定性对配电网的冲击。在联合发电方面,好多学者对此作了相关研究,如在光电、风电上纳入了储能装置,形成了光储、风储发电系统,利用储能装置调节作用,来减少分布式电源出力的波动性。文献[2]考虑了光储系统内对配电网有功及无功的调控作用,较传统配电网无功优化增加了光储系统有功、无功控制变量,以网损及电能质量为目标,对多场景进行优化对比。但是其没有考虑负荷的时序性和随机性,只是对配电网进行了静态无功优化;文献[3]针对DG出力和负荷的时序及随机性,建立二层规划优化模型,但其并未涉及分布式电源联合发电。在风光储联合发电系统(Wind-Photovoltaic-Energy Storage Hybrid System,WPESHS)方面,文献[4]建立了风、光联合出力的概率模型并添加储能控制策略,探讨了不同储能配比、风光装机配比对其可信容量的影响及风光联合接入时的互补效益;文献[5]针对风光储系统连续供电方面进行研究,以蓄电池作为储能设备进行优化配置,并建立蓄电池内部模型,通过仿真分析对比确定模型的准确合理性。总的来说,大多文献是对风光储联合出力模型的可靠性进行研究,没有分析风光储联合发电系统对配电网网损及电能质量的影响。
在传统配电网中,为了降低网络损耗、保证电能质量,大多采用无功优化装置。而对于含离散变量的主动配电网无功优化这一非凸非线性规划问题,在数学上缺少有效的求解方法。针对这一问题,文献[6]基于罚函数与内点法的结合,将含离散变量的非线性整数规划问题转化为连续整数规划问题;文献[7-8]利用二阶锥松弛技术对优化模型进行转换,将含离散变量的规划问题扩展为混合整数二阶锥规划(MISOCP);此外,很多文献基于二阶锥规划利用不同的优化变量使建立的目标函数最小,文献[9]基于多种主动管理措施,以投资费用最小进行规划分析,运用二阶锥规划模型进行算例验证;文献[10]以补偿电容为优化变量,将经济效益最大作为目标函数,使用二阶锥规划模型对结果进行检验;文献[11]先将电网分区,以无功补偿装置为优化变量,使用二阶锥规划方法验证其优化模型的可行性。
文中考虑分布式电源出力及负荷用电的时序性及随机性,对含WPESHS的配电网进行分时段无功优化,通过协调优化分布式电源出力及优化控制无功补偿装置来降低配电网网络损耗以及减小节点电压偏差,利用凸松弛技术将主动配电网无功优化模型转换为含离散变量的MISOCP模型。在IEEE 33节点系统上进行仿真,对比分析不同分布式电源发电类型及配置无功优化装置的情况下,配电网功率损耗及电压偏差的情况。
1 WPESHS的数学模型
风光储联合发电是利用风电、光电时空的不互补性及储能系统对功率的平抑作用的发电方式,可平滑其输出功率,减少对配电网的冲击,从而改善电能质量提高系统稳定性[12]。
1.1 风光机组数学模型
风力、光伏出力具有不确定性,其输出功率的数学模型是随时间变化的随机概率模型。文中为简化WPESHS模型,以某日某地的风力、光伏有功出力预测序列为基础,为使总有功功率输出适应配电网需求,对储能装置进行充放电。
风力、光伏的出力约束方程为:
(1)
(2)

1.2 储能装置数学模型
对于储能装置,它在WPESHS中起调节作用,适应配电网负荷需求。当配电网可用出力能够满足负荷功率需求时,储能装置处于充电状态;反之,储能装置会补充发电[4]。通过储能装置的调节作用来适应当前负荷用电。
图1所示为储能系统的调控策略。
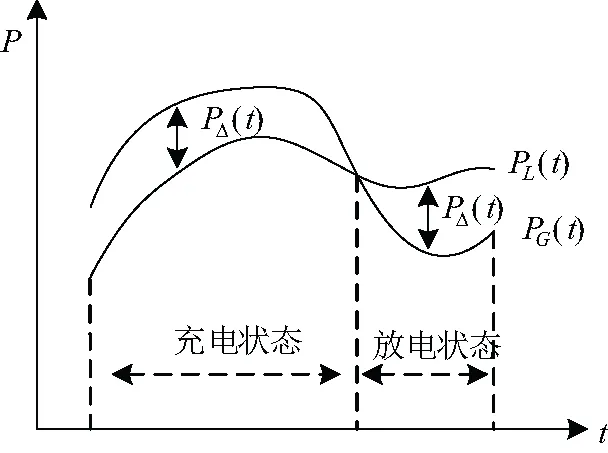
图1 储能装置充放电控制示意图Fig.1 Schematic diagram of charge and discharge control for energy storage devices
图1中PG(t)为配电网可用出力曲线;PL(t)为负荷用电曲线;PΔ(t)为可用机组出力与负荷功率需求差值,即PΔ(t)=PG(t)-PL(t)。
储能装置功率约束方程为:
(1)当0≤PΔ(t)≤PE.max时,为充电状态。
(3)
(2)当-PE.max≤PΔ(t)<0时,为放电状态。
(4)
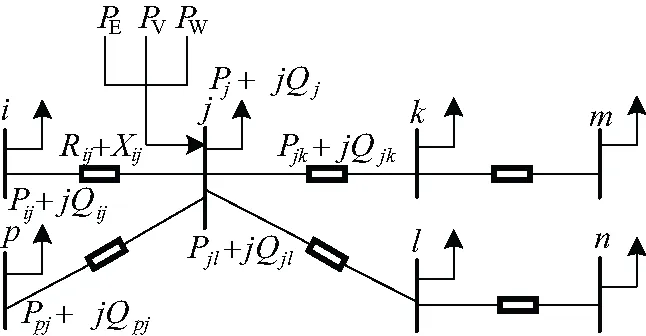
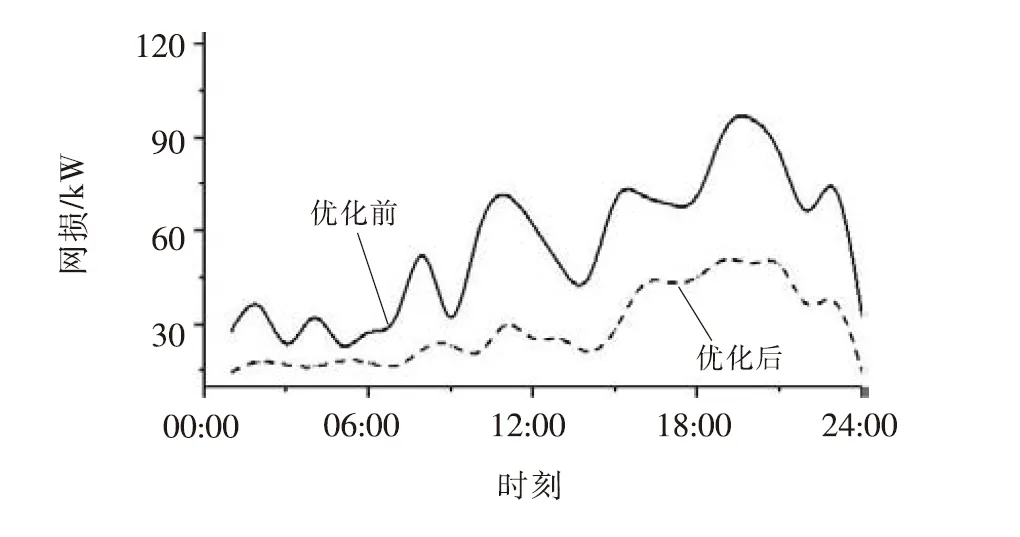
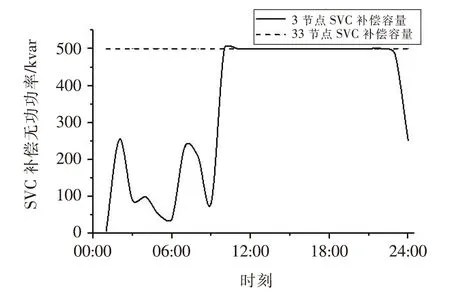
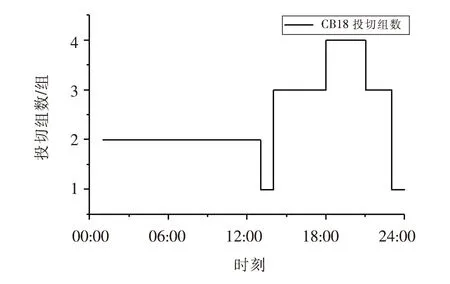
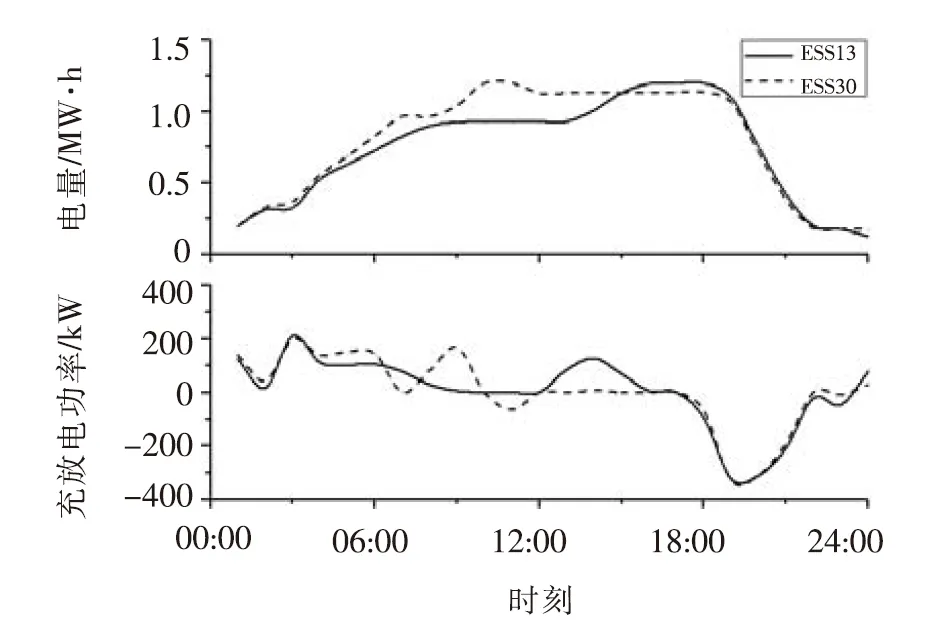
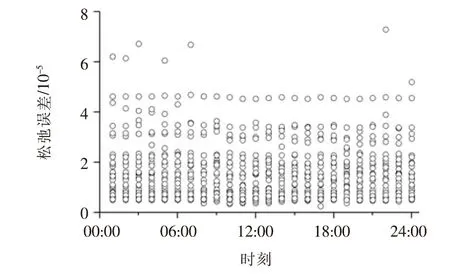
(3)当PE.max 式中E(t)、E(t-1)分别为在t、t-1时刻储能装置的容量;Emax为储能装置的最大储能容量;δ为储能装置自放电系数;ηc、ηf分别为储能装置充、放电效率;PE.max为储能装置最大充放电功率。 (1)辐射状配电网的Distflow[13]支路潮流方程 配电网DistFlow潮流模型如图2所示。 图2 含风光储发电系统的辐射状配电网Fig.2 Radiation distribution network with wind-photovoltaic-energy storage generation system 支路潮流方程如下。 对于节点j: (5) 对于支路ij: (6) 式中: Pj.DG.t=Pj.V.t+Pj.W.t+Pj.E.t (7) Qj.DG.t=Qj.V.t+Qj.W.t (8) 式中ψ(j)为以j为支路末端节点的首端节点集合;φ(j)为电网中以j为支路首端节点的末端节点集合;Pij.t、Qij.t为t时刻支路ij的有功、无功功率;Pj.DG.t、Qj.DG.t分别为WPESHS发出的有功、无功功率;Iij.t、Uj.t分别为t时刻支路ij电流和节点j电压;Rij、Xij为支路ij的电阻与电抗;Pj.V.t、Pj.W.t、Pj.E.t为t时刻节点j的光伏、风电及储能装置的有功出力;Qj.V.t、Qj.W.t为t时刻节点j的光伏与风电的无功出力;Pj.d.t、Qj.d.t为t时刻节点j负荷的有功、无功功率;Qj.com.t为t时刻节点j的无功补偿功率。 (2)配电网的运行安全约束 (9) 式中Uj.min、Uj.max、Iij.max分别代表节点电压的上下限和支路电流限值。 (3)主网关口约束 (10) 式中Ps.min、Ps.max、Qs.min、Qs.max分别为主网关口节点的有功、无功功率输出限值。 (4)分布式电源约束 (11) -Pj.E.max≤Pj.E.t≤Pj.E.max (12) (1)分组投切变压器(Capacitor Banks,CB)运行约束: (13) (14) (2)静止无功补偿装置(Static Var Compensator,SVC)运行约束: QSVC.min≤QSVC.t≤QSBC.max (15) 式中QSVC.min、QSVC.max为SVC补偿的上下限值。 文中以系统网络损耗最小及节点电压偏差最小建立多目标优化函数,通过控制无功补偿装置来使目标函数最小,多时段目标函数为: F=min(floss,fΔU) (16) (17) (18) 式中Ploss为系统一个调度周期的有功网损;Iij,t、Ui,t为t时刻支路电流及节点电压;Rij为支路阻值;ΔU为系统一个运行周期的节点电压偏差之和;UN为额定电压。 对于上述多目标函数,文中使用层次分析法分配权重将其处理为单目标函数,因为两目标量纲不同,所以对上述目标函数进行归一化处理。 f′loss=Ploss/Pmax (19) f′ΔU=ΔU/ΔUmax (20) 式中Pmax为未接入任何优化装置的网络损耗,ΔUmax为节点电压一周期内的最大电压偏差之和,对于提高电压质量目标来说,其各节点电压偏差取值范围简单取为(0,5%),所以得最终单目标优化函数为: (21) 式中η1、η2为权重系数,反应对电网运行损耗及电能质量的偏好,也称偏好因子,且η1+η2=1,运用层次分析法计算得η1=0.634,η2=0.366。 主动配电网优化问题实质上是一个非凸非线性规划问题,且考虑到优化装置的离散性。文中利用二阶锥规划(Second-Order Cone Programming,SOCP)对优化模型进行处理。 标准形式[14]如下: (22) 式中 变量x∈RN;系数常量b∈RM、c∈RN、AM×N∈RM×N;K分为如下两种形式。 标准二阶锥: (23) 旋转二阶锥: (24) (25) 根据文献[15],可将式(25)松弛为: (26) 然后做等价变换,化为标准二阶锥形式: (27) 用上述变量替换以上潮流方程相关项有: (28) 松弛后的数学模型为: (29) 由于优化装置的离散变量的介入,原本二阶锥凸规划扩展为MISOCP。 文中使用MATLAB编写程序,以Yalmip为平台调用Cplex求解器进行求解。使用如图3所示的IEEE 33节点配电网系统进行无功优化模拟分析,该系统以辐射状运行,电压等级为12.66 kV,全网负荷功率为3715+j2300 kVA。配置参数为:节点13和30接WPESHS,风电机组容量为600 kVA,光电机组容量为400 kVA,储能装置充放电容量范围为0~400 kW·h,最大储能容量为1 200 kW·h,充放电效率为0.938 1。无功优化策略为:在节点3和33接入SVC(SVC3,SVC33),节点5和18接入分组投切电容组(CB5,CB18),参数选择依照文献[16]。 图3 IEEE 33节点图Fig.3 IEEE 33-node diagram 采用某地典型DG出力曲线及日负荷曲线,为了简化模型,文中以1 h为步长,输入24个风光发电离散功率序列,根据归一化处理的日负荷曲线计算得出33节点的24 h负荷曲线,如图4所示。 图4 分布式电源出力及负荷用电曲线Fig.4 Curve of DG output and load demand 为了验证含WPESHS的配电网无功优化模型对配电网网损及电压质量的改善作用,文中以一天作为优化周期,选用4种情景下的配电网进行优化模拟,情景A:不含分布式电源;情景B:含风、光单独发电系统;情景C:含风光互补发电系统;情景D:含WPESHS的配电网。 表1为对4种情景的优化仿真结果,其中包括24 h的网损之和、弃风弃光量、平均节点电压偏差及降损率。 表1 4种情景的优化结果Tab.1 Optimization results of 4 scenarios 与情景A相比,情景B的网损量降低50.66%、平均节点电压偏差降低0.9%,而情景C分别降低59.05%和1.05%,可见为当风电、光电机组纳入辐射状主动配电网,电源的接入会影响到主动配电网馈线中的功率流动,并且风电、光电会提供一定的无功功率,可以适当减少网络损耗减少电压偏差。 与情景A相比,情景D周期内的网损量及平均节点电压偏差分别降低63.33%和1.09%,均高于情景B、C的减少量,表明同时加入储能控制变量在降损调压方面效果更佳。这是因为从图4风光出力曲线图可看出,分布式电源的峰值与负荷用电峰值不在同一时刻,对于没有接入储能装置的情景B、C在风光出力最多时会由于负荷轻而弃风弃光,对于接入储能装置的情景D由于储能装置的调节作用,配电网能合理利用分布式电源,更好的降低网络损耗并提升电压水平。 在弃风弃光方面:1与情景B相比,情景C的弃风弃光总量减少1 360.957 7 kW,可见利用风光互补性的发电方式,能降低其出力波动,增加电网对DG的消纳能力,减少弃风弃光;2与情景C相比,虽弃风弃光有所改善,但仍有一定量的弃风弃光,而情景D的弃风弃光量基本为0,可见利用风光机组的互补性,虽然能有效降低出力的波动,但其出力调节能力有限,而再加入储能装置,利用储能变量的调节作用,在整个运行周期内合理调配资源,进而能更好的提高电网的消纳能力。以上几点说明,文中含WPESHS的配电网优化模型的合理性。 (1)优化前后结果对比 图5为对含WPESHS的配电网进行无功优化前后24 h的网损图。从图中可得,在以上优化策略下,网损降低效果十分明显,并且在重负荷的时间段(07:00-22:00)降损效果尤为明显。 图5 优化前后网损图Fig.5 Network loss graph before and after optimization 图6为优化前后节点30的电压变化曲线。从图中可知,优化后电压与优化前相比有明显上升,且优化前后电压峰谷差分别为0.018、0.013,优化后的电压波动性降低、平稳性提高。可见文中的优化策略是可行且有效的。 图6 优化前后30节点电压变化曲线Fig.6 Voltage change curve of 30-node before and after optimization (2)优化控制策略分析 文中系统总负荷在3 715 kW,而每个接入点的DG有功总和为1 000 kW,由于此渗透率下,过电压情况不明显,所以SVC主要为容性补偿。如图7所示,SVC3不同时段的补偿容量可看出,在轻负荷时段(0:00~7:00),SVC3无功补偿容量较少,而在重负荷时段(10:00~23:00),SVC3补偿处于较高水平。如图3所示,节点33为配电网的末端节点,根据辐射状配电网运行的特点,节点离变电站越远其电压水平越低,所以SVC33补偿容量一直处于较高水平。 图7 两组SVC的补偿容量Fig.7 Compensation capacity for two sets of SVCs 图8为CB18投切控制策略,CB由于严格的操作次数限制,CB18在负荷较轻时段保持较低的补偿,而在分布式电源出力较少且负荷用电较多的时段(14:00~21:00)有效调整其投切组数。 图8 CB18的投切组数Fig.8 Number of cast-cutting groups for CB18 图9为两组储能装置的电量及充放电控制策略,在负荷较轻且分布式电源出力较多时段(00:00~18:00),节点电压偏高,网损较少,这时ESS会吸收分布式电源发出功率以便在重负荷时释放电能,降低运行周期的总损耗。并且在储能装置出力较多时段(18:00~22:00),在此时段无功补偿装置CB投切组数也处于较高水平。 图9 ESS电量及充放电功率Fig.9 Electric quantity and charge and discharge power of ESS 为了检验二阶锥松弛后式(26)的精确性,定义松弛偏差指标ΔDij.t: (30) 图10为二阶锥松弛偏差的散点图。明显,松弛后的偏差是非常小的在10-5量级左右,文中使用的二阶锥松弛是可行的。 图10 松弛误差散点图Fig.10 Scatter for relaxation deviation 文章主要对含WPESHS的主动配电网,以网损电压偏差最小为目标函数,建立无功优化模型,通过SOCP对优化模型进行求解。结果显示,文中建立的含WPESHS的配电网优化模型,能发挥其对配电网的无功补偿及有功调控的作用,有效降低网络损耗及减小电压偏差,并一定程度的增强了配电网对DG的消纳能力。并且相比其他DG发电系统,其调压降损效果能为明显。此外,对文中采用的二阶锥规划进行松弛准确性校验,结果显示,二阶锥凸规划在精确性有良好的特性。2 主动配电网动态优化模型
2.1 配电网的运行约束

2.2 无功优化装置运行约束
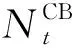
2.3 目标函数
3 二阶锥规划
3.1 二阶锥模型
3.2 无功优化模型的SOCP松弛
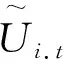
4 算例分析
4.1 算例参数

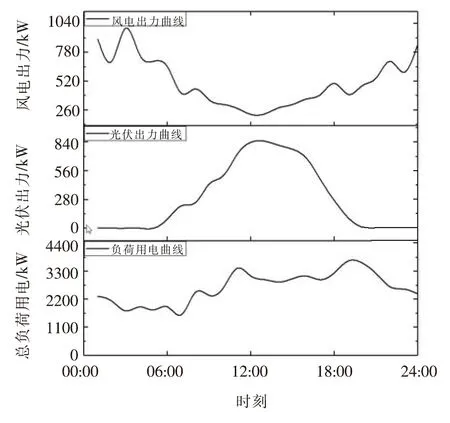
4.2 多种情景优化结果分析

4.3 含WPESHS的配电网优化控制策略

4.4 松弛准确性
5 结束语
