一种面向电力物联网的认知D2D网络能效资源分配算法
2023-03-02黄兴张文杰李曦张瑜李保罡贾惠彬
黄兴,张文杰,李曦,张瑜,李保罡,贾惠彬
(1.国网辽宁省电力有限公司,沈阳 110004; 2.华北电力大学(保定) 电子与通信工程系,河北 保定 071000)
0 引 言
随着智能电网与电力物联网技术的发展,电力设备间互通互联及互操作成为智能电网发展的新趋势。高效的通信方式是实现电力物联网通信与设备间信息化控制的关键问题。第五代移动通信系统的低延时、大容量和高可靠等特点越来越受到智能电网的青睐[1-3]。而认知无线电与D2D通信结合形成的新型基于认知的D2D网络,用户可通过发现附近可复用的蜂窝用户频谱,并且获得临近增益和信道复用增益,从而提高数据传输容量和可靠性,在5G移动通信技术方面发挥着重要作用[4]。
然而,D2D通信也带来了新的问题和挑战,因为蜂窝用户的链路资源被重用,并且不能忽略内部干扰。在实际的认知D2D通信场景中,设备的电池寿命对通信质量也有一定的影响。目前,关于认知D2D网络资源分配的研究主要集中在频谱效率优化、吞吐量及能效等。文献[5-6]提出了一种传输速率最大的自由分配算法,没有考虑用户之间的竞争关系。针对系统总速率最大化的问题,文献[7]提出了一种基于博弈论的资源分配算法。建立了博弈模型,证明了在一定条件下博弈具有唯一的纳什均衡点,并且提出了一种不完全信息重复博弈者决策的学习方法。文献[8]考虑D2D用户具有能量收集能力,研究认知D2D网络下行用户总吞吐量最大化的联合功率控制和信道分配策略。针对认知多播D2D网络,为了减小蜂窝用户对D2D用户分簇组的干扰影响,文献[9]研究了系统总容量最大的信道分配与功率控制算法。为了实现在基站接入模式和D2D 模式下进行灵活的选择式接入,文献[10]提出了一种进化论方法研究D2D 用户接入蜂窝网络的模式问题,来实现D2D 用户总用户数据速率最大的资源分配问题。针对认知D2D 全双工通信网络中存在的频谱资源共享导致的干扰问题,文献[11]提出了D2D用户速率最大的资源分配算法,从而提高了系统的谱效和传输速率。考虑完美的信道状态信息,文献[12]提出了一种能效最大的资源分配算法,但是该方法没有考虑干扰功率约束,无法保证蜂窝用户的通信质量。基于博弈论,文献[13-14]研究了认知D2D 网络能效最大化的资源分配问题,在用户通信干扰门限约束下实现能效和谱效的均衡。
然而,由于信道时延、随机无线电环境干扰、量化/重构误差等因素的影响,使得系统获得完美的信道状态信息是不切实际的。因此需要提前将这些参数不确定性的影响考虑到资源分配算法中,保证算法的鲁棒性,降低中断概率,保证数据传输的可靠性。尤其满足智能电网控制业务对数据传输高可靠性和低延时等要求。
基于上述分析和存在的问题,本文研究认知D2D网络鲁棒能效最大的资源分配问题。首先,考虑D2D用户最大发射功率约束、蜂窝用户最大功率约束和干扰功率约束,建立下垫式频谱共享模式下认知D2D网络上行传输的资源分配模型。其次,考虑蜂窝用户干扰中断约束,基于最小最大概率机和辅助变量法,将原非凸优化问题转换为凸优化求解。然后,基于凸优化理论,获得鲁棒资源分配问题的解析解。最后,仿真结果表明,该方案具有很好的性能,可以为电力物联网通信架构设计提供参考。
1 系统模型
如图1所示。
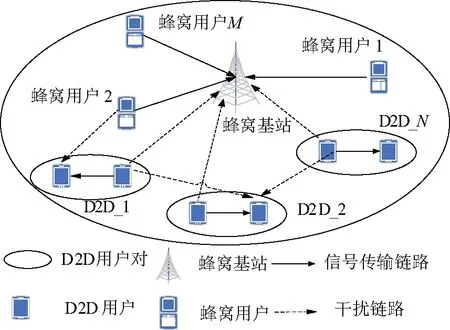
图1 多用户下垫式认知D2D通信网络Fig.1 Multi-user underlying cognitive D2D communication network
本文使用的是一个频谱共享模式下多用户下垫式(underlay)认知D2D通信系统。此系统有1个蜂窝基站,M个蜂窝用户,N对D2D用户,且用户集合分别定义为∀m∈{1,2,…,M}和∀n∈{1,2,…,N}。蜂窝系统频谱资源被划分成多个子信道,且每个蜂窝用户利用一个正交的子信道进行上行数据传输,这样避免了蜂窝用户之间的同层干扰影响。假设每对D2D用户具有频谱认知能力,灵活地实现模式选择和资源调度,提高蜂窝频谱资源的利用率。由于是基于下垫式频谱共享模式,因此D2D用户在复用蜂窝用户频带资源的时候需要控制其干扰功率不超过特定的门限值,且假设所有无线信道服从瑞利分布。
假设任意的D2D用户对n共享第m个蜂窝用户的频带资源进行数据传输。考虑蜂窝用户对D2D用户的干扰和其他D2D用户对当前D2D用户的干扰,因此第n个D2D用户接收机的信干噪比为:
(1)
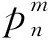
(2)
定义每对D2D用户的电路功耗为pc,则所有D2D用户的总功率消耗为:

(3)
进一步考虑到需要对每个蜂窝用户的通信质量进行保护,有如下干扰功率约束:
(4)

考虑到D2D用户电池容量的限制,其发射功率不能无穷大,因此传输功率满足如下约束:
(5)
式中pmax为第n个D2D用户能够提供的最大发射功率。
为了使得D2D网络能效最大,同时满足每个蜂窝用户的通信质量,考虑上述分析结果,基于能效最大的资源分配问题为:
(6)

2 鲁棒资源分配算法
考虑信道估计误差的影响,实际的信道增益可以用如下加性不确定性模型描述:
(7)
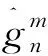
(8)
式中ξm为蜂窝用户m的中断概率门限值。显然该问题是一个NP-hard问题,难以直接获得资源分配问题的解析解。
2.1 中断概率转换
针对中断概率约束,已经有很多常用的方法来进行处理,例如,松弛概率积分法[15]和伯恩斯坦近似不等式方法[16]。然而,上述方法都需要知道不确定参数的概率统计分布模型。但是在实际的认知D2D网络中,由于不存在用户间合作情况,因此很难获得该统计分布信息。另外,由于无线信道的随机性,也使得提前假设某一特定的概率分布模型失效。因此,需要引入新的机制来解决该问题。
最小最大概率机能够很好的解决上述问题。最小最大概率机是一种处理中断概率的优化方法,该方法只需要估计误差的均值和方差信息,并不需要这些参数服从某一特定的概率分布。基于这一特点,可以有效解决统计模型未知的中断概率转换问题。基于最小最大概率机方法,任意中断约束可以描述为如下形式:
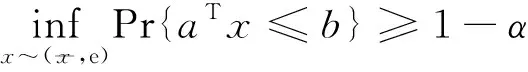
(9)
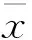
(10)
其中:
(11)

(12)
结合式(11)和式(12)可以得到:
(13)
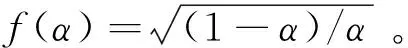
(14)
式(14)为约束式(9)等价的闭式形式,且第一项为估计值,第二项为估计误差带来的摄动项。
(15)
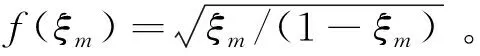
(16)
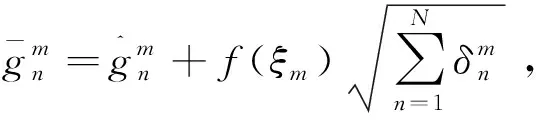
2.2 凸优化问题转换
目标函数是分数形式,该问题是在凸约束条件下的非凸优化问题,基于Dinkelbach方法[17],目标函数可以等价为:
(17)
式中η为D2D用户总的能效且η≥0。由于速率函数中发射功率耦合关系,基于连续凸近似方法[18],传输速率可以近似为如下等价凸形式:
(18)

因此目标函数式(17)可以等价为:
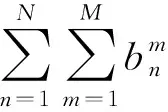
(19)
因此,结合式(16),式(19)和式(8)可以得到如下凸优化问题:
(20)
式(20)是一个凸优化问题,可以利用凸优化理论[20]获得资源分配的解析解。
2.3 鲁棒资源分配算法求解
利用拉格朗日原理可以求解问题(20),构建优化问题式(20)的拉格朗日函数为:
(21)
式中λm≥0和βn≥0为拉格朗日对偶变量。式(21)可以等价描述为:
(22)
因此,对于每个D2D用户而言有:
(23)
根据拉格朗日对偶原理和式(21),对偶问题为:
(24)
其中对偶函数D(λm,βn)的表达式为:

(25)
根据KKT条件和次梯度更新方法[21],可以得到资源分配算法的解析解如下:
(26)
(27)
(28)
(29)
式中s1和s2为迭代步长;[x]+=max(0,x);t为迭代次数。当设置合适的步长因子,能够保证算法快速收敛[22]。
3 仿真结果
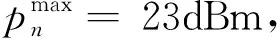
图2给出了在不同用户数量下的认知D2D网络用户的能效的关系。从图中可以看出,系统总的能效随着D2D用户数量的增加而增大。但是当D2D用户成倍的增大时,系统的能效并不跟随成倍增加。其原因是因为多个D2D用户之间的同频干扰会增加当前活动用户的干扰,从而使得原存在网络的用户信干噪比有所降低。另外,本文鲁棒算法比传统非鲁棒算法的能效要高。随着中断概率门限的增大,本文算法的能效逐渐增大。因为大的中断概率门限意味着干扰功率约束中的有效传输功率减小,从而对蜂窝用户提供更好的保护性能。

图2 用户能效与D2D用户数量之间的关系Fig.2 Relationship between user energy efficiency and the number of D2D users

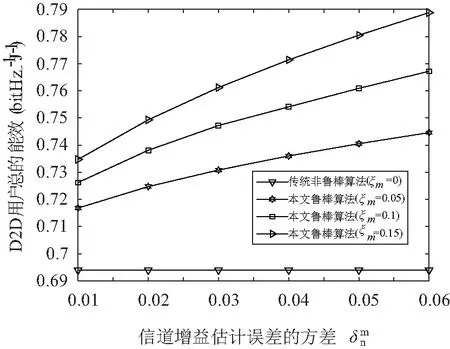
图3 D2D用户总能效与中断概率门限的关系Fig.3 Relationship between the total energy efficiency of D2D users and the outage probability threshold

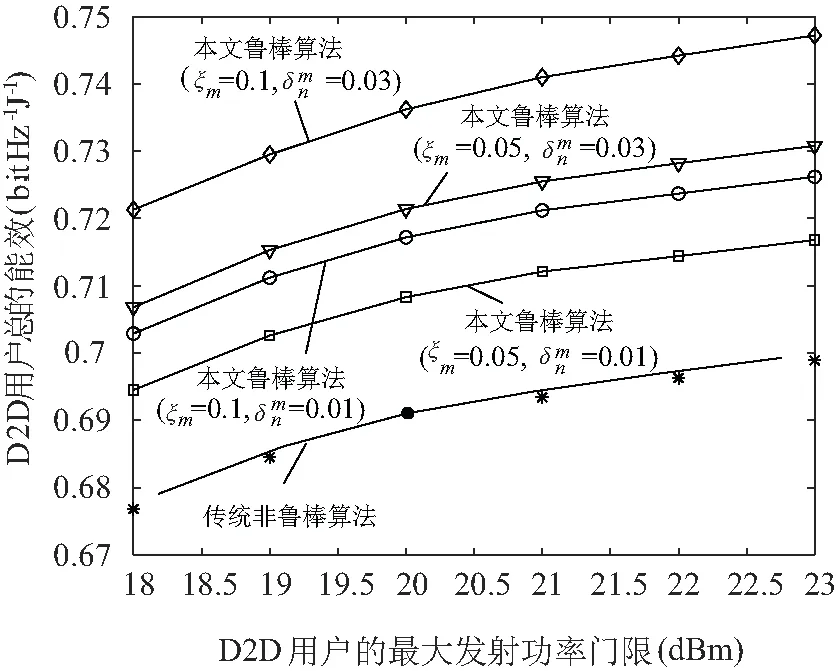
图4 在不同发射功率下不同算法能效性能对比Fig.4 Comparison of energy efficiency performance of different algorithms under different transmission powers


图5 D2D用户能效与最大干扰功率门限的关系Fig.5 Relationship between D2D user energy efficiency and the maximum interference power threshold

表1 算法性能差异对比Tab.1 Algorithm performance difference comparison
4 结束语
为了提高认知D2D网络的在电力物联网应用中的能量效率和鲁棒性,本文考虑不完美CSI的影响提出了一种D2D用户总能效最大的鲁棒资源分配算法。考虑D2D用户最大发射功率约束和蜂窝用户共道干扰约束,建立能效最大的资源分配模型。基于最小最大概率机、Dinkelbach方法和连续凸近似方法解决非凸优化问题。再利用拉格朗日对偶原理求解所转化成的凸优化问题。仿真结果表明本文所提的算法具有较好的能效并且能够保证蜂窝用户的通信质量。该方案可应用于配电物联网,可实现监测装置间收发机的快速互联交互,也可用于配电自动化系统,提高数据传输的可靠性与能效。
