试验设计及参数优化的LS-SVR显著性因子筛选①
2023-03-01崔庆安
崔庆安, 崔 楠
(1. 上海海事大学经济管理学院, 上海 201306; 2. 武汉大学经济与管理学院, 武汉 430072)
0 引 言
高质量产品是企业赢得竞争优势的关键.在工业4.0时代,随着制造过程复杂化以及顾客需求日益苛刻,对质量优化的要求也日渐提高.传统方法基于经典线性模型,难以描述复杂的质量形成规律,优化结果仍有较大提升空间.因此,形式灵活的机器学习模型被引入到质量优化.然而此类模型具有“黑箱”特性,虽然可以实现全局建模,但内部结构解析程度低,难以对质量形成规律给出有说服力解释,显著影响了使用者信心.如何增强该类模型应用于质量优化的可解释性,是亟待解决的科学问题.事实上,即使在机器学习范畴,“可解释性(interpretability)”也是当前研究难点[1, 2].对于制造过程,质量优化主要途径之一是参数优化,即通过选择合适的加工工艺参数值,使产品质量特性达到最优.而机器学习模型应用于参数优化的瓶颈,是如何根据模型解释各工艺参数对质量特性影响的显著程度,进而识别关键工艺参数,降低质量优化难度与成本.
制造业实际中,由于过程噪声影响,工艺参数与质量特性之间呈统计相关而非确定性函数关系,因此很难建立精确数学模型.目前多是通过试验设计(design of experiments,DOE)[3]获取样本集,拟合工艺参数与质量特性之间的经验回归模型,而后寻优得到质量特性优化值及对应参数值.在试验设计建模及参数优化中,工艺参数被称为“因子”,质量特性被称为“响应”,首先需确定“因子—响应”回归模型的基本形式.因子试验,响应曲面分析(response surface methodology,RSM)[4]等等,采用一阶、二阶多项式模型,这是一种局部模型,对于较为复杂的作用关系(例如响应存在多个极值,因子与响应高度非线性相关)效果有限[5, 6].为此,研究者采用非参数模型[7],试图在可行域全局范围内近似“因子—响应”的作用关系.此类模型形式灵活,其前提假设弱化为响应的光滑变化,而不要求与因子线性相关.Vining和Bohn[8]最早将核函数回归(kernel function regression,KFR)应用于印刷过程质量优化;此后采用非参数模型进行实验设计建模的研究逐渐丰富[9, 10].除KFR外,高斯过程回归(Gaussian process regression,GPR)或Kriging模型也被引入试验设计建模,用于无重复误差的计算机试验[11].也有研究者将上述模型应用于实际过程的质量预测与参数优化[12].近年来,研究者还将机器学习中的人工神经网络(artificial neural networks,ANN)与试验设计结合[13],利用样本数据训练权值并拟合作用关系模型[14].KFR,GPR,ANN优势在于其较强的非线性拟合能力,但此类模型均是基于“经验风险最小化”,即认为拟合性能好则预测性能也好.这是一种大样本渐进性理论,只有样本量足够大,预测性能才与拟合性能一致[15],较典型的是ANN的“过拟合”现象.由于试验设计样本量较为有限,上述模型效果也受到限制.虽然可以通过改善训练过程来降低“过拟合”,但是目前并没有非经验性方法来确保得到预测性能好的模型.
作为改进,支持向量回归机(support vector regression,SVR)[16]被引入到试验设计建模及参数优化.SVR是目前最佳的小样本机器学习工具,基于“结构风险最小化”,能够平衡拟合误差与模型复杂度,在有限样本下取得较好预测性能,更适合于试验设计建模:崔庆安和何桢[17]给出了SVR应用于试验设计建模及参数优化的基本框架,验证了SVR相对于KFR,ANN的优势.孙林和杨世元[18]利用正交设计建立铣削表面粗糙度的SVR模型,得到稳健优化结果.向国齐和殷国富[19]针对两杆结构,提出基于SVR和粒子群算法的稳健优化方法,与经典RSM,ANN和Kriging对比说明了SVR优势.曲兴田等[20]提出基于SVR和粒子群的焊点布置优化方法.Zhou等[21]分析了SVR,径向基函数,GPR在稳健性优化中的应用,验证了此类模型对于多项式的优势.
上述研究表明,非参数和机器学习模型形式灵活,应用于复杂作用关系过程的试验设计建模及参数优化优势明显;然而这种灵活性也带来了“可解释性”差的弊端[8],较难提供类似于经典线性模型的推断性统计解释,很大程度上降低了使用者对模型的信任,主要表现之一就是难以实现显著性因子筛选(factors screening).显著性因子是指在统计意义上对响应有影响的因子,而非显著性因子引起的响应变化则较小,与随机波动区别不明显,将非显著性因子剔除可以简化作用关系模型.在实际制造中,只需控制显著性因子(对应为关键工艺参数),而允许其他工艺参数在较宽范围波动,从而降低制造难度和成本.
线性回归模型是“因子—响应”结构形式,表现为因子及其系数加权和,各因子(或交互作用)以分立形式存在,可以借助系数的显著性检验来判断因子显著性.此类研究较为成熟,包括部分因子设计与超饱和设计[5],贝叶斯方法[22],序贯分支方法[23]等等.然而对于非参数和机器学习模型而言,其结构的“可解释性”差是本质问题;表现为所有因子在模型中以整体样本点而非分立形式存在.这是一种“样本点—响应”结构,难以直接考察因子影响.例如KFR,GPR,SVR模型结构为核函数及其系数加权和,所有因子作为样本点,整体由核函数进行映射变换,很难转化成“因子—响应”结构.而对于ANN,其复杂的网络联结以及非线性激励函数映射,使因子与响应之间的影响变得更加难以探查和解释.
目前基于非参数和机器学习模型进行显著性因子筛选的成果还很少.而与之相关的,对于复杂作用关系过程的显著性因子筛选研究可分三类:其一是直接应用线性模型.刘丽君和马义中等[24]将序贯分支方法应用于供应链仿真,考虑位置与散度效应筛选显著性因子;施文等[25]研究了基于动态效应的序贯分支方法.但是序贯分支方法以多项式模型为基础,且假设各因子对于响应的影响方向已知,并不完全适用于非参数或机器学习模型.此外,Xue和Wang等[26]利用偏相关分析识别舰载机陆下沉速度的关键影响参数,并利用Kriging建模,但识别依据是线性显著性,而且需在模型拟合之前进行.其二是根据非参数和机器学习模型特点,直接从样本点角度考察显著性.崔庆安[27]采用SVR拟合过程作用关系模型,利用因子可行域内的支持向量比率,来识别显著性样本点.该研究者[28]进一步基于最小二乘SVR进行序贯设计及建模,构造了样本点显著性检验的正态分布统计量.此类方法虽然可以识别出显著性样本点,但是并未单独识别出各因子显著性.其三,在计算机试验中,可采用灵敏度分析识别关键因子.即改变各因子水平,根据响应协方差计算Sobol指数,较大者即对应关键因子.该方法只能给出各因子的相对重要度,难以判断其统计显著性.Kleijnen[29]采用序贯分支方法对Kriging模型进行变量筛选.Denimal等[30]将GPR或Kriging模型拓展到随机误差情形,对于此类过程,Sobol指数较难区分因子或噪声影响.如何利用非参数和机器学习模型,从统计显著角度检验因子显著性,仍然值得深入研究.
本研究将开展试验设计条件下的机器学习模型的显著性因子筛选研究.考虑到SVR模型在样本量有限时的优良性能,将其选作基础回归模型,利用推断性统计检验,从该模型的“样本点—响应”结构中直接筛选显著性因子.进一步地,采用最小二乘SVR(least squares support vector regression,LS-SVR)代替标准SVR进行研究.与标准SVR相比,LS-SVR的拟合值是观测值线性组合,更有利于构造推断性统计量[31].本研究首先介绍LS-SVR基本原理;而后提出基于重复观测样本集的LS-SVR模型拟合不足的近似F-检验方法;进而提出两阶段的显著性因子筛选方法;最后通过仿真与实证说明方法的有效性.
1 理论简介
LS-SVR是一种回归估计方法.设p维变量x=[x1,…,xp]T∈X与一维随机变量y∈Y之间存在未知依赖关系y=f(x)+ε,其中ε~N(0,σ2)为随机误差.回归估计就是利用来自于总体(X,Y)的训练样本集={(xi,yi),i=1,…,n}去拟合f(x).根据f(x)形式及拟合方法不同,形成各类回归模型.例如多项式形式的线性模型
(1)
LS-SVR将f(x)的形式设定为
f(x)=wTφ(x)+b
(2)
其中φ(x):Rp→H是非线性映射函数,w是权值向量,改变φ(x)可得不同f(x)形式.利用样本集进行估计,建立LS-SVR模型的优化函数为
s.t.yi=wTφ(xi)+b+ξii=1,2,…,n
(3)
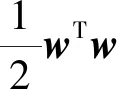

(4)
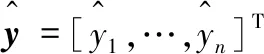
(5)
由于Ω、Z-1、c仅与xi有关,于是L与y无关,则Ly是y的线性组合或称线性光滑(linear smoother),有利于推断性统计:设E(y)=μ,Var(y)=σ2I,则E(Ly)=Lμ,Var(Ly)=σ2LLT,E(yTLy)=σ2trace(L)+μTLμ.
2 方法研究

2.1 LS-SVR模型拟合不足的近似F-检验方法
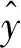
1)重复观测的样本集与LS-SVR拟合模型.设x共有m个不同水平,有xi=[xi,1,…,xi,p]T,i=1,…,m.在每个xi处各有ni次重复试验,其观测值为yi,j,j=1,…,ni;假设ni个yi,j独立同分布即yi,j~N(f(xi),σ2),则建模样本集可表示为
(6)
(7)

(8)
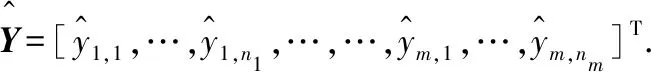
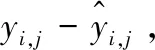

定义SSPe为“纯误差平方和”,表示重复观测值与其平均值之差的平方和
=(Y-MY)T(Y-MY)=YT(I-M)Y

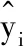
SSRes=SSPe+SSLof
上式即为残差平方和的分解等式,在此基础上,可以发展出相应的显著性检验方法.
3)拟合不足均方与纯误差均方比值的近似F-分布.由定义,SSRes、SSPe和SSLof均为半正定二次型,其对应矩阵为ARes=I-2L+L2、APe=I-M和ALof=M-2L+L2.根据二次型理论,SSPe和SSLof的自由度分别为dfPe= tr(APe)=n-m和dfLof=tr(ALof)=m-tr(2L-L2).将平方和除以自由度,即可得纯误差均方MSPe、拟合不足均方MSLof
MSPe=SSPe/dfPe;MSLof=SSLof/dfLof
(9)
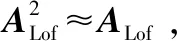
F0=MSLof/MSPe~FdfLof,dfPe,λLof,λPe
(10)

E(MSPe)=σ2+ET(Y)APeE(Y)/tr(APe)
(11)
E(MSLof)=σ2+ET(Y)ALofE(Y)/tr(ALof)
(12)
可以证明ME(Y)=E(Y)②,则易证ET(Y)APeE(Y)=0及λPe=0、E(MSPe)=σ2,于是MSPe可以作为σ2的无偏估计.
4)LS-SVR拟合不足的显著性检验及方差分析表.该检验的原假设H0和备择假设H1可设为

F0=MSLof/MSPe~FdfLof,dfPe
(13)
而当模型拟合不足时,根据半正定二次型性质,有ET(Y)ALofE(Y)>0因而E(MSLof)>σ2,E(MSLof)>E(MSPe).式(14)中,将有可能出现较大的F0,其显著性P-value为
P-value=Prob.{F0>Fα,dfLof,dfPe}
(14)
其中α是某个显著性水平值(例如0.05).由此可得拟合不足检验的方差分析表:
式(13)中,当ni增大时,n将增大,dfPe=n-m也将增大;但是dfLof=m-tr(2L-L2) 的变化与ni的相关性不高:因为m与ni无关,而tr(2L-L2)与2L和L2的接近程度有关,受不同样本点数目m影响较大,与单个样本点重复次数ni无关.对于F-分布而言,当第二自由度(即dfPe)增大时,反映其不对称性的指标“偏斜”将减少,显著性检验的稳健性将增加,因此增加重复试验次数将有利于显著性检验.但是ni也不能无限制增加,还需受到实验成本与时间约束.
2.2 基于拟合不足检验的LS-SVR模型显著性因子筛选
1)利用两阶段的LS-SVR模型考察因子的显著性.其一是对初始LS-SVR模型的拟合不足检验,此时所有因子x1,…,xp均参与建模.根据样本集0拟合出初始的LS-SVR模型M(0),其中xi=[xi1,…,xip]T,i=1,…,m.如果由式(13)和式(14)来计算出的P(0)-value<0.05,则有较强理由认为M(0)存在拟合不足.此时应该重新选择和优化模型的超参数,或者增加新的建模样本点,重新拟合模型,直至拟合不足不显著为止.
其二是改变参数建模的因子组合,拟合新的LS-SVR拟合模型,再进行拟合不足检验考察各因子(组合)的显著性.对于x=[x1,…,xp]T若需考察其中某个因子xk的显著性,一个比较直观的思路,是将xk从x中移除,形成新的因子组合x(-k)=[x1,…,xk-1,xk+1,…,xp]T及建模样本集
(15)
而后拟合新的LS-SVR模型M(-k).如果M(-k)拟合不足,则说明不能将xk移除,其对y有显著影响.而这种显著性的大小,可以用P(-k)-value来表示.该值越小,说明因子xk的移除对模型影响越大,因而xk也就越显著.若需考察因子组合xc=[xc1,…,xck]T,{c1,…,ck}⊂{1,…,p}的显著性,可将xc从x中移除,而后拟合新的LS-SVR模型进行拟合不足检验.还可根据各因子(组合)P-value值的相对大小进一步比较其显著性.

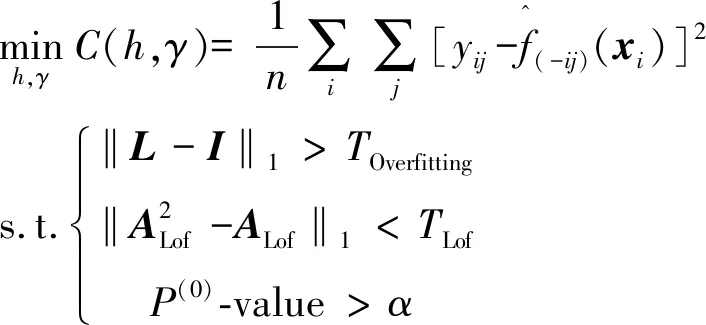
(16)
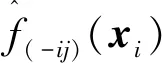
其二,关于M(-k)超参数的选择.LS-SVR模型结构主要由h2、γ以及样本集来确定,可以依样本集分布而光滑变化.仅仅根据样本集(-k),改变h2、γ也可得到某个拟合模型M′(-k).但是与M(0)相比,M′(-k)的h2、γ和xi均发生了变化,不论其拟合不足的显著性如何,均不能看作是仅仅由于将xk移除而导致的.为反映xk移除对于M(0)的影响,恰当做法是将M(0)的h2、γ直接应用于M(-k).由于样本观测值yi,j在(-k)与M(0)中保持一致,此时变化的只有因子组合,由含有xk的xi变为移除xk的如果M(-k)出现拟合不足,则说明不能移除xk,其对于LS-SVR拟合模型而言是显著的.
2.3 显著性因子筛选的实现步骤
根据上述分析,形成试验设计条件下基于LS-SVR拟合不足检验的显著性因子筛选步骤.总体上可以分为初始模型拟合,显著性因子筛选两个阶段.基于研究的聚焦性,假设已经确定了合适的试验设计方式.
阶段I初始模型拟合检验.

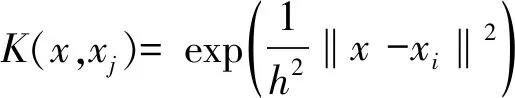
步骤3利用表1和式(13)、式(14)对M(0)进行拟合不足检验,如果P(0)-value<0.05,则说明M(0)存在拟合不足,此时需返回步骤3,重新选择h2和γ,直至拟合不足不显著.

表1 LS-SVR模型拟合不足检验的方差分析表
阶段II显著性因子筛选阶段.
步骤4令k=1,…,p,依次将xk从x中移出,得到x(-k)=[x1,…,xk-1,xk+1,…,xp]T,以及如式(15)所示的新建模样本集(-k),采用和M(0)相同的h2和γ,形成简化后的拟合模型M(-k).
步骤5对M(-k)进行拟合不足检验,计算P(-k)-value,其值越小,说明xk越重要.
步骤6k=1,…,p,重复步骤4、步骤5,将得到的各P(-k)-value由小到大排序P(-1′)-value≤P(-2′)-value≤…≤P(-p′)-value,该序列即是各因子显著性程度由高至低排序.在0.05的显著性水平下,P(-k)-value<0.05对应的xk均可看作显著性因子,其余因子均不显著.

步骤8对比分析步骤6与步骤7的结果,确定可以从LS-SVR模型中移除的不显著因子,得到显著性因子组合以及对应的简化模型M(Red.).
需要说明的是,表1的计算与核函数形式无关,可以适用于各种形式的核函数(例如多项式核,B-样条核等等);但是需要根据其不同的超参数类型,参照式(16)进行约束最优化求解,以使ALof满足近似幂等的条件.
3 仿真研究
利用两个典型仿真函数,考察MSLof与MSPe比值的近似F-分布的经验概率密度曲线与理论概率密度曲线的符合性;对基于拟合不足检验的因子显著性筛选方法进行仿真验证.
3.1 仿真函数
仿真函数I是带有白噪声的Camel函数
(17)
其中ε~N(0,σ2);x1,…,x6∈[-2,2].上式中仅含有x1或x2的部分是Camel函数,已被应用于各类算法仿真[34].fCamel在x1,x2维度上较为显著,如图1所示,而对于因子xt,t=3,4,5,6,其对应系数均为0,本质上不显著性.对于fCamel,一阶、二阶多项式难以实现全局性建模.但若采用高阶多项式,将会导致“维数灾难”.例如6因子六阶多项式,需估计529个系数;若只考虑不超过三阶的交互作用,则需估计101个系数.因此采用LS-SVR进行全局性建模.

图1 Camel函数的3维和2维投影图
仿真函数II是有工程背景的Piston函数,由一系列非线性函数组成链式结构,用于对活塞在气缸内的圆周运动建模[35],其形式为
(18)

3.2 仿真过程
根据仿真函数范围fCamel∈[0, 9.866 7]+ε,fPiston∈[0.164 2, 1.199 1]+ε,各选取两个噪声水平σ以及因子水平组合数m.fCamel仿真:σ=0.5,1.0;m=50,100;fPiston仿真:σ=0.05,0.1;m=50,100.而后在每一(σ,m)组合处各进行10次仿真.每次仿真的因子水平组合由LHS设计生成,表示为x1,…,xm,且规范化至[0, 1]内.对于每个xi,随机生成重复试验次数ni≤3.根据利用式(17)、式(18)生成初始样本集,利用3.3节步骤识别出显著性因子(或因子组合).作为对比,利用LHS设计生成大小为1 000的预测样本集,分别计算初始和简化LS-SVR模型的预测均方误差MSPE.对于相同的xi,ni和σ,固定LS-SVR超参数不变,重复5 000次试验,得到含有随机噪声的响应观测值.根据式(9),计算出5 000个F0=MSLof/MSPe值,由此估计出对应的经验概率密度曲线(采用核估计方法);再根据式(10)计算理论概率密度曲线.
3.3 仿真结果
1)关于近似F-分布的经验与理论概率密度曲线.由上述过程得到fCamel和fPiston各40组经验与理论概率密度曲线,如图2(a)、图2(b)所示.
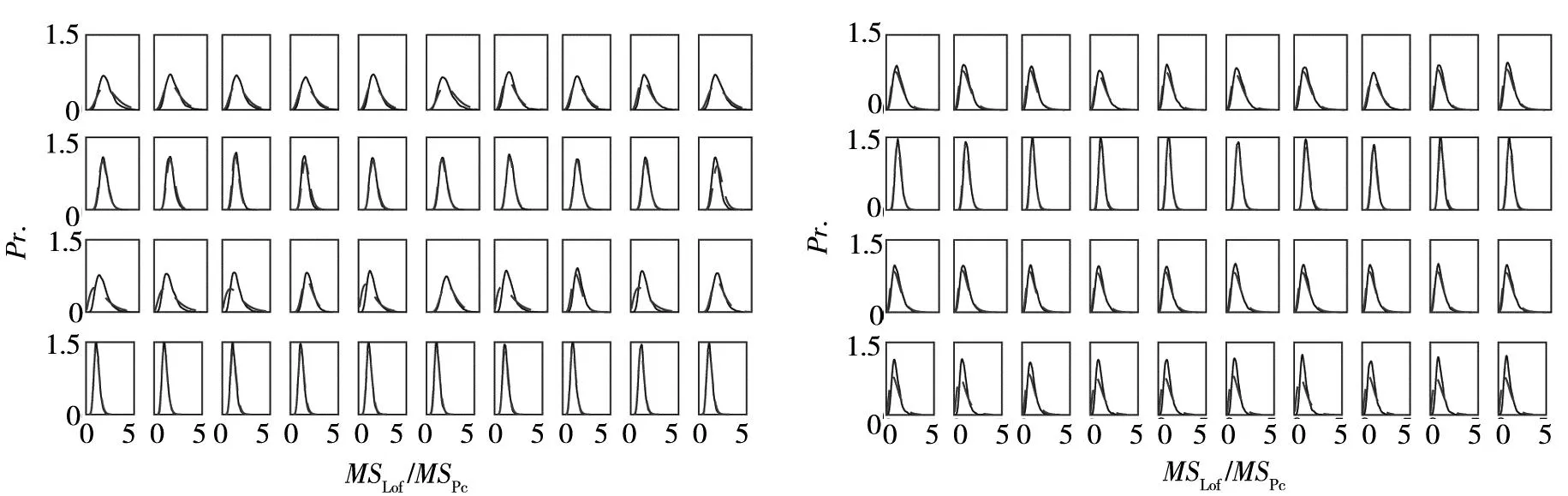
(a) fCamel (b) fPiston
2)关于显著性因子的筛选.表2和表3为fCamel和fPiston仿真的显著性因子筛选,给出了移除某个因子后的LS-SVR模型拟合不足P-value.该值越小,被移除因子对模型影响越为显著.表中还给出了能够被移除的最大因子组合.
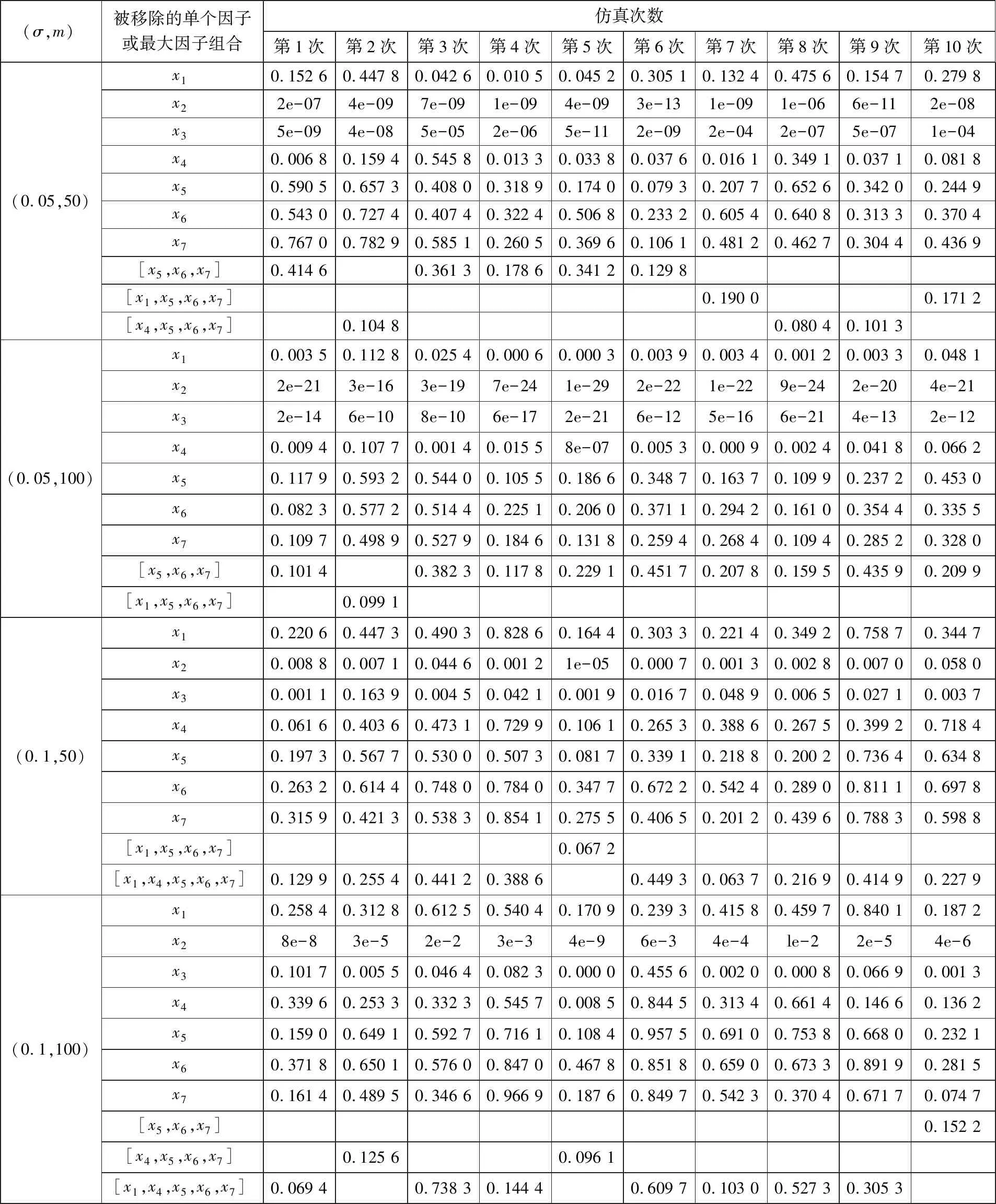
表3 fPiston仿真的拟合不足P-value
以表2的(σ,m)=(0.5,50)为例,设定显著性水平为0.05,第1次仿真,单独移除x1或x2,模型均出现拟合不足,P-value分别为4e-11和9e-17(科学计数法);而单独移除x3、x4、x5、x6中任一个,P-value均大于0.05,不会导致拟合不足.如果将因子组合[x3,x4,x5,x6]移除,拟合不足也不显著(P-value=0.294 9).包含x1或x2的因子组合共45组,将其分别移除后所得P-value最大值为1e-12,拟合不足均为高度显著;而对于所有不包含x1或x2的因子组合(共11组),分别将其移除后P-value均大于0.05,拟合不足均不显著.此时,最大因子组合是[x3,x4,x5,x6],而[x1,x2]即为显著性因子.
为进一步说明,表4给出了fPiston,(σ,m)=(0.05,50)第1次仿真确定可移除的最大因子组合的过程:首先发现因子x1,x5,x6,x7对应的P-value均大于0.05,于是考虑将该因子组合移除;但发现移除后P-value=0.032 6<0.05,因而不能整体移除;而后考虑移除其中3个因子,计算得知,因子组合[x5,x6,x7]对应P-value= 0.414 6,而其他3因子组合P-value均小于0.05,不能被移除.由此可移除的最大因子组合为[x5,x6,x7],对应的显著性因子为[x1,x2,x3,x4].

表4 LS-SVR模型的不显著因子移除过程示意
3)关于简化后的LS-SVR模型的预测性能.为考察移除不显著因子对LS-SVR模型影响,利用表2和表3的样本集,采用拟合均方误差MSE和预测均方误差MSPE来对比初始模型M(0)和简化模型M(Red.)性能,每次仿真均由LHS设计生成一个大小为1 000的测试样本集.而后相同(σ,m)的10次仿真形成一组Box图,fCamel和fPiston各形成4组对比Box图,如图3和图4所示.
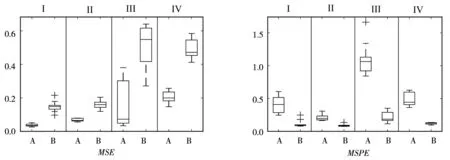
“I”,“II”,“III”,“IV”对应(σ,m)为 (0.5, 50),(0.5, 100),(1.0, 50),(1.0, 100);“A”初始模型,“B”简化模型
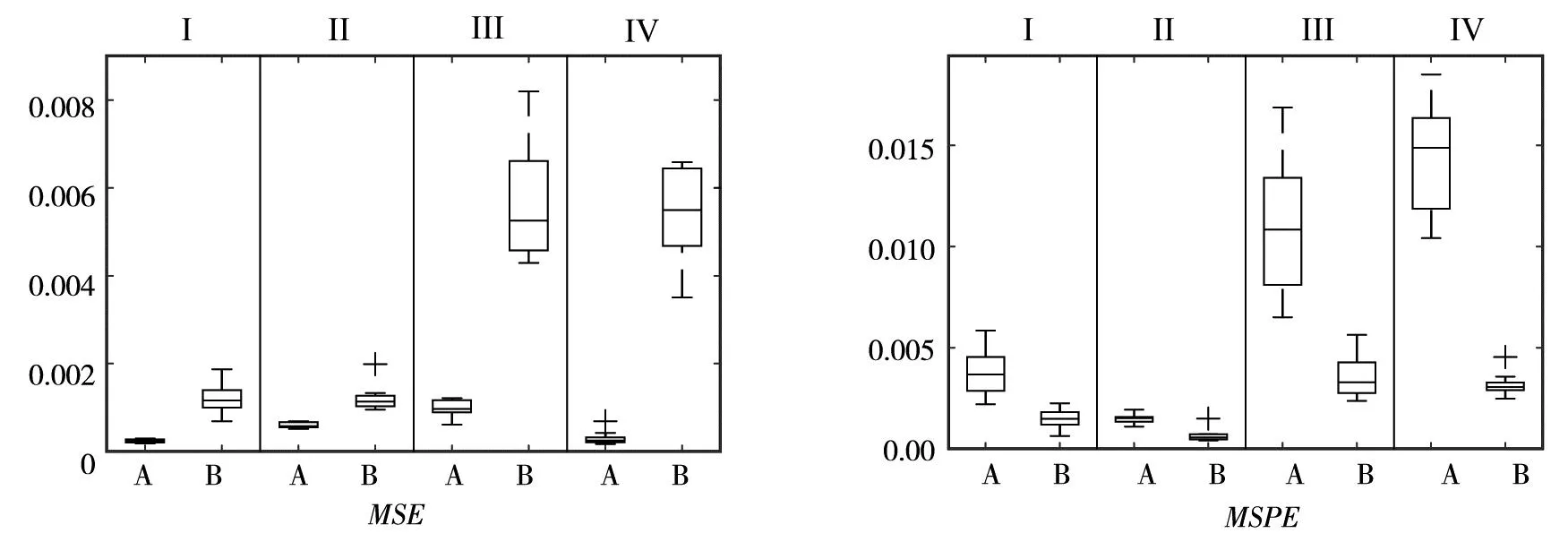
“I”,“II”,“III”,“IV”对应(σ,m)为 (0.5, 50),(0.5, 100),(1.0, 50),(1.0, 100);“A”初始模型,“B”简化模型
4)关于与逐步回归方法的对比.在经典理论中,与显著性因子筛选相关的交叉验证法主要有逐步回归法(step wise regression,SWR)[36],序贯分支法等等.后者无法包含二阶主效应,有可能会引起残差的异方差.因此采用含一阶、二阶主效应以及二阶交互作用效应的线性回归模型,运行SWR方法.其模型为

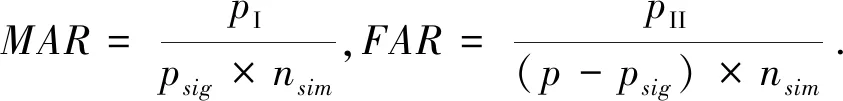

表5 各类方法识别出的显著性因子及漏判率、 误判率对比(fCamel)
4 实证研究
4.1 案例背景
3D打印可以应用于汽车,航空航天,医用材料等领域,是智能制造的代表技术之一[37].熔融沉积成型是使用最为广泛的3D打印技术,其基本原理是将高分子等热熔性材料从喷嘴处挤出,分层堆积凝固形成实体.此过程的工艺参数主要包括层厚、打印速度、喷嘴温度、热床温度、填充率、最短冷却时间等等;质量特性则包括零件的尺寸精度及形状符合度等等.成型过程需经历从固态到熔融,再到冷却成型的复杂变化,使得工艺参数与制成品质量特性之间呈高度非线性相关.对于大多数3D打印制成品而言,翘曲(warping)和飞边(flash)是主要质量缺陷,而通过基于试验设计建模的工艺参数优化,可以较为显著性地降低翘曲程度和飞边长度.然而上述工艺参数的影响大小不一致,在质量优化之前,需要先识别出显著性因子,以降低优化控制的难度.考虑到3D打印过程的强非线性,这里采用所提出的LS-SVR建模和显著性因子筛选方法,再通过遗传算法寻优,得到优化的工艺参数值及质量特性值,并通过试验验证有效性.
试验设备为“Z-603S”型“极光尔沃”牌3D打印机.采用直径1.75 mm的聚乳酸材料进行打印.试验零件为15 mm×15 mm×3 mm的立方体.工艺参数分别为层厚/(mm):x1∈[0.06,0.20],打印速度/(mm/s):x2∈[20,70],喷嘴温度/(℃):x3∈[190,220],热床温度/(℃):x4∈[50,70],填充率/(%):x5∈[20,50],最短冷却时间/(s):x6∈[3,6].质量特性为翘曲/(mm):ywarp和飞边/(mm):yflash,均为望小型.采用游标卡尺进行测量,以制成品水平放置时,其表面距离水平面的最大高度为ywarp,以各条边的最大飞边长度为yflash.
4.2 试验设计样本集获取及显著性因子筛选

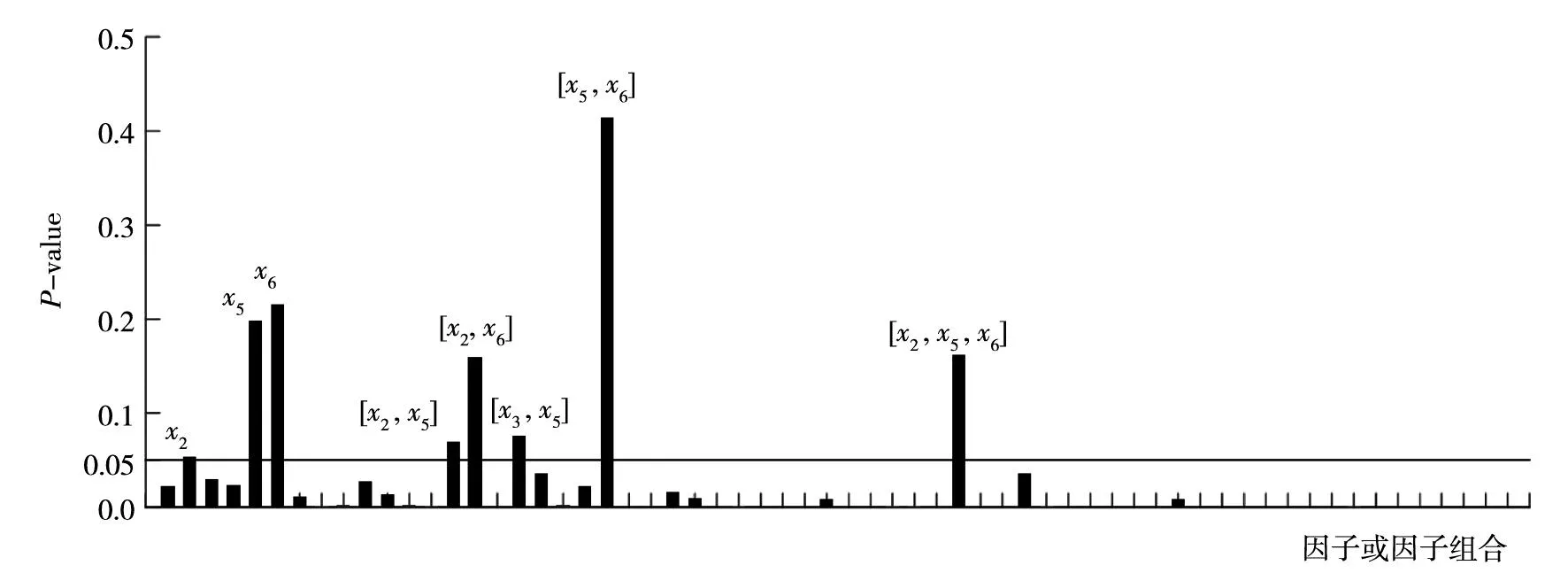
图5 3D打印过程因子(或因子组合)移除后的拟合不足显著性
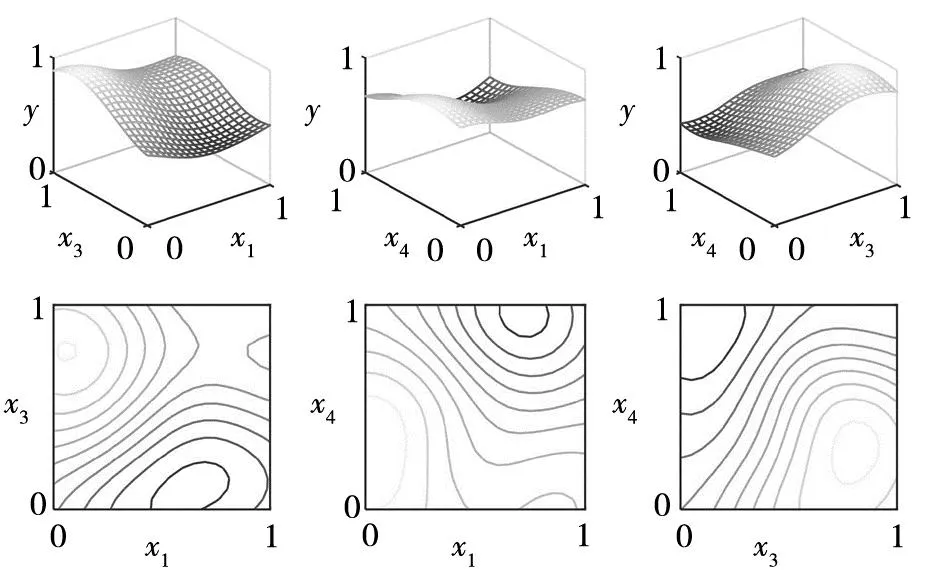
图6 3D打印的简化LS-SVR模型曲面及等高线
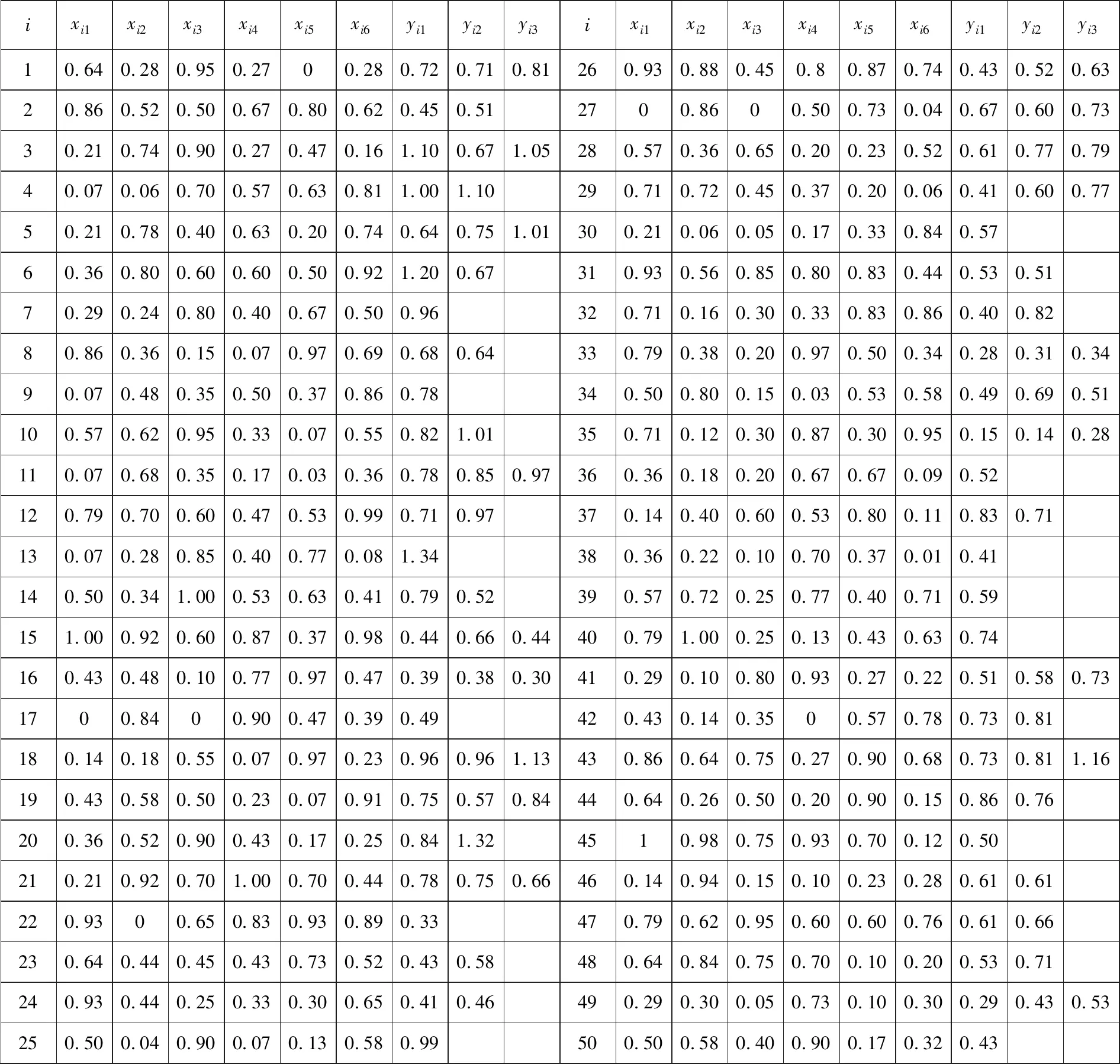
表6 3D 打印试验LHS设计的因子组合及响应值
4.3 质量特性寻优
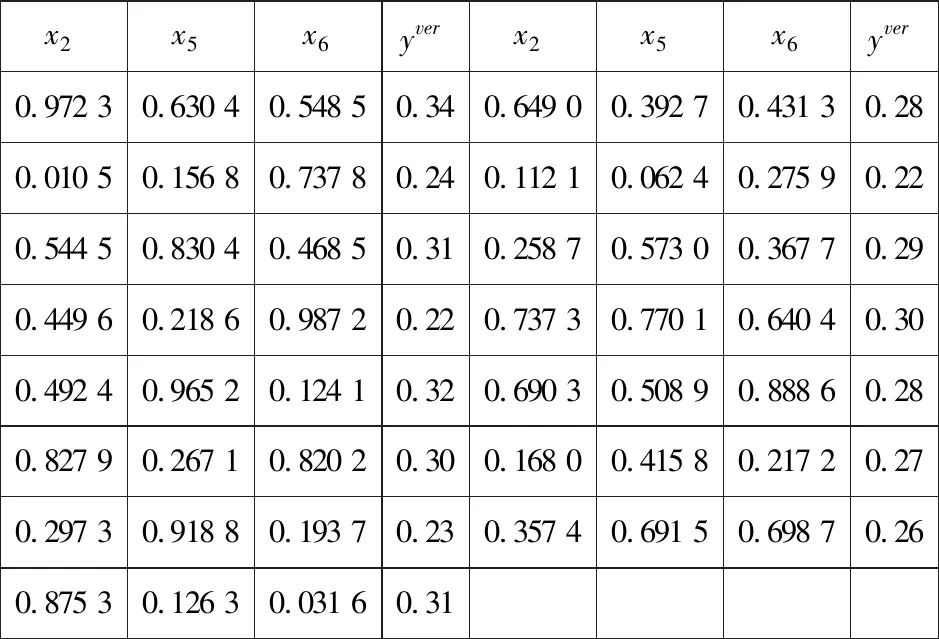
表7 3D打印的简化LS-SVR模型寻优结果验证试验
5 结果讨论
5.1 所提方法的有效性
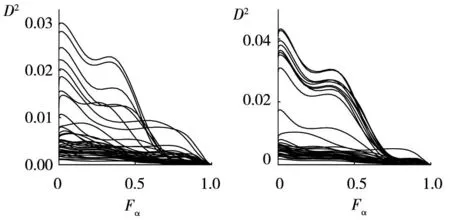
1)非中心F-分布的符合性.从图7(a)和图7(b)可以看出,非中心F-分布的经验与理论概率密度曲线的符合程度较好.
(a)fCamel (b)fPiston
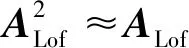
其二,经验与理论概率密度曲线的尾部符合性更高,对于较为显著的拟合不足判断影响较小.拟合不足意味着存在一个较大MSLof/MSPe,对应在曲线右偏尾部位置.图7表明,两类曲线的差异主要集中在最高点附近,而尾部差异不大.作为归一化,采用各概率密度相对于近似F-分布(理论分布)分位数Fα的曲线作为参照,定义
其中ge(Fα)和gt(Fα)表示Fα处的经验和理论概率密度,D2(Fα)表示累积到Fα处的两类概率密度曲线的偏差均方.图7(a)和图7(b)给出了fCamel与fPiston仿真的D2(Fα)曲线.可以看出,当Fα较大(例如>0.5)时,D2(Fα)呈快速减小趋势.
2)显著性因子识别及简化模型结构的一致性.表2和表3说明,所提方法能够有效识别显著性因子,给出可移除的不显著因子最大组合.
其一,所提方法在识别显著性因子方面的一致性较高.fCamel的40次仿真,x1、x2均被识别为显著,其对应的拟合不足P-value均较小;与作为白噪声添加进模型的不显著因子x3、x4、x5、x6对应的P-value有明显差异;40次仿真中,37次(比例为92.5%)识别出了所有不显著因子.fPiston的40次仿真,x2有39次(比例为97.5%)被识别为显著,x3有35次(比例为87.5%)被识别为显著;40次仿真中,能够被移除的最大因子组合均包含[x5,x6,x7].
其二,简化模型的基本结构具有一致性.表2和表3说明,σ和m不同,被移除最大因子组合不同,对应的简化模型也不同.fCamel的(σ,m)=(0.5,50)第1次仿真,得到了含有x1、x2的简化模型;而(σ,m)=(0.5,50)第10次仿真,得到了含有x1、x2、x4的简化模型,但是所有40次仿真,真实的显著性因子x1、x2均被无差别识别并包含于简化模型.也就是说,简化模型基本一致,且描述了初始模型主要特征.对于fPiston,其仿真函数没有特别加入权重系数为0的白噪声因子,但是40次仿真中,x2、x3均包含于简化模型,说明了简化模型结构的基本一致性.
3)简化模型复杂度降低和预测性能改善.直观理解,如果将某些因子移除,模型表现能力将降低.但图3和图4说明,与初始模型相比,简化模型拟合误差增加,但预测误差却明显降低.
其一,简化模型的预测均方误差MSPE降低且波动减小.对于fCamel和fPiston,简化模型的拟合性能降低,表现为拟合均方误差MSE的均值和波动性均有所增加,但是预测均方误差MSPE却优于初始模型,并且其IQR(四分位距)也有明显减小,说明方法预测性能也较为稳定.
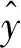
5.2 与经典线性模型显著性因子筛选方法的比较
1)均是以F-分布和方差分析为基础.所提方法基于式(10)的近似F-分布和方差分析,与经典线性模型相比,这也是一种统计检验方法.因此在单次检验中,会由于过程噪声σ影响,得到不同的显著性结果,表2和表3也说明,最终被移除的最大因子组合不完全相同.但在多次重复检验下,某个因子组合将会以较大概率出现,例如表2中的[x3,x4,x5,x6]和表3的[x5,x6,x7],这也是统计检验方法的特点.类似地,经典线性模型中,对于同一个“因子—响应”过程,不同观测值也可能导致不同的显著性因子筛选结果.

3)对于样本量大小的要求不同.经典线性模型的F-分布要求样本量n→+∞.然而试验设计建模样本量一般有限且较小.而所提方法的近似F-分布不以n→+∞为基础,试图在有限样本条件下通过调整LS-SVR超参数h2与γ来获得,具有较强的工程实践现实意义.再者,近似F-分布对于样本量的要求与LS-SVR模型本身的小样本特性是一致的,更有利于体现模型性能,图3和图4也说明,通过近似F-分布剔除不显著因子得到的简化模型,其预测性能得到了较好改善.
4)关于因子效应的“稀疏性”、“交互作用”与“因子组合”的显著性.因子效应的“稀疏性”指试验设计中的重要因子(即显著性因子)是少数的[38].例如析因试验中,只有一部分因子效应呈现为统计学意义上的显著,而其他(尤其是高阶交互作用的效应)不显著.本研究也体现了这一原则,对于3D打印试验,总计6个工艺参数,能够被同时移除的有3个,其余为显著性因子.由于LS-SVR模型的特点,所提方法未涉及各因子间的交互作用.“交互作用”项指线性模型的因子乘积项(例如x1x2).LS-SVR模型中不存在因子乘积项,而实际制造过程也不存在能够单独控制的“交互作用”项.所提方法可以从因子组合整体(而非多个因子简单加和)角度判断显著性,可以较好地适应实际过程参数优化和控制的需要,3D试验也说明了这一点.
5)与逐步回归方法的“漏判率”与“误判率”对比.从表5可以看出,所提方法的MAR与FAR均优于SWR方法.所提方法的MAR在不同m与σ组合下均为0,而SWR方法最高达0.15,意味着在10次仿真中有3个(次)显著性因子未被有效识别出.所提方法的FAR最高为0.075,而SWR方法最高达0.275,是本文方法的3.67倍.此外,当σ增大时,所提方法的FAR均变为0,更适合于工程实践噪声较大的情形.
6 结束语
本研究根据LS-SVR特点,提出了基于拟合不足检验的显著性因子筛选方法,用以在试验设计建模及参数优化中识别关键工艺参数、降低质量改进成本.利用LS-SVR线性光滑估计的特点,将拟合模型残差平方和分解为拟合不足与纯误差的平方和;利用重复性试验,给出了拟合不足与纯误差均方比值的近似F-分布,构造了拟合不足检验的方差分析表;利用移除某个因子(组合)导致的拟合不足显著性P-value的变化,提出了显著性因子的筛选方法;还通过增加满足近似F-分布的约束,给出了LS-SVR模型的超参数选择方法.仿真与实证研究表明,本研究较好地实现了具有“样本点—响应”及核函数结构的机器学习模型的显著性因子筛选,简化了模型形式,改善了预测性能.本研究有助于增强在试验设计建模及参数优化中应用LS-SVR模型的“可解释性”,有利于从因子(而非样本点)角度探究其影响,拓展机器学习模型在质量改进的应用.所提方法也适用于大数据集的因子显著性筛选.一般而言,大数据集缺乏严格的重复性样本集,可以考虑将某一样本点附近较小邻域内的样本点近似作为重复测量.而邻域半径的确定、近似重复性对于显著性检验的影响等等,是需要进一步研究的问题.
