一种新的基于辛空间的密钥预分配方案

陈尚弟 张俊梅

(中国民航大学 天津 300300)

1 引言

无线传感器网络是由若干低成本且资源有限的传感器节点组成的一种分布式传感器网络，无线传感器网络技术是在计算机技术中的突破和创新，作为一种新型的信息收集和处理技术，具有耗能低、成本低、功能齐全等优点，有着非常广阔的发展前景[1]。随着它的广泛应用，网络安全问题也受到人们的重视。节点在部署到目标区域后容易受到敌方攻击，如信息在传输时被窃听、篡改、泄密等。在现代密码学中，信息的保密性主要取决于密钥的保密性，因此如何管理密钥成为一个极具挑战的问题。密钥预分配是指节点在部署到目标区域前就将密钥分配给各个传感器节点。所有的密钥预分配方案分为密钥预分配阶段、共享密钥发现阶段和路径密钥建立阶段。

通常从以下4个方面来分析一个密钥预分配方案是否可行：

(1)网络规模：方案所能支持的最大传感器节点数目。

(2)密钥环大小：每个节点所能存储的密钥量。

(3)连通概率：网络中任意两个节点之间有共享密钥的概率，通常用p表示。

(4)损失概率：当s个节点被捕获时，一条随机链接被破坏的概率，通常用f ail(s)来表示。

若某个节点被敌方捕获，则该节点内存储的所有密钥均被泄露。假设节点Nk被捕，并且节点Na和节点Nb的 共享密钥存储在Nk中 ，此时Na和Nb之间的链接就断开了，Na和Nb之间的链接称为损失的链接。网络的损失概率反映了网络中节点的抗捕获能力，损失概率越大，节点抗捕获能力越弱。fail(1)为 当一个随机节点被捕获时，节点Na和Nb之间的链接被断开的概率。由此可估算fail(s)=1−(1−fail(1))s。f ail(s)也可通过式(1)表达式直接求得

自Camtepe等人[2]首次提出利用组合设计构造密钥预分配方案之后，许多基于组合设计的密钥预分配方案被提出。2010年Pei等人[3]基于有限域上有理正规曲线构造了一个密钥预分配方案，分析了基于该设计下的密钥预分配方案的连通概率和损失概率。2015年Bag[4]将网络分区，每个小区内有普通节点和簇头两种传感器节点，簇头的数量取决于小区的大小。2017年Chen等人[5]基于可分解设计和有限域上辛几何构造了一系列密钥预分配方案。2018年Kumar等人[6]将网络分区，限制每个小区内的簇头数量为3，且将每个小区的通信范围限制在给定小区的 Lee球体区域内。这种做法既提高了节点的抗捕获能力又降低了对节点的存储要求。2019年Akhbarifar等人[7]描述了一种可扩展的无线传感器网络安全模型，并提出了一种基于组合设计的混合密钥预分配方案。提出了无线传感器网络的安全性仿真方法，并与以往的类似方案进行了比较。同年袁琪等人[8]基于w−平衡不完全区组设计构造了一个密钥预分配方案。2020年Pang等人[9]分析了基于正交阵列汉明距离的密钥预分配方案中用于评估连通性和弹性的度量的计算可以简化。随后在文献[10]中给出精确的基于正交阵列的密钥预分配方案的弹性的计算公式。研究了基于正交阵列的广播增强密钥预分发方案的连通性和弹性。同年Choudhary等人[11]提出了一种基于多项式的密钥预分配方案，讨论和分析了不同的密钥分发协议，并提出了基于稀疏矩阵的高度安全的多项式池密钥分发技术，以降低存储和计算复杂度。2021年Belim等人[12]提出了一个广义的密钥预分配方案，密钥材料是基于向量空间元素和向量空间上的对称算子形成的。

近年来国内外对密钥预分配方案的研究很多，但基于各参数未达到最优，本文将在这一方面做研究。本文利用有限域上辛空间中子空间之间的正交关系构造了一个组合设计，并基于该设计构造一个密钥预分配方案。与其他方案相比本方案中节点的抗捕获能力非常好，并且随着网络规模的扩大，方案的连通概率逐渐趋于1。本文创新点为基于有限域上的辛空间构造了一个组合设计，并基于该设计构造了一个密钥预分配方案。基于辛空间构造的密钥预分配方案较少，方法上具有一定的创新性。

2 预备知识

本节介绍组合设计(区组设计)和有限域上辛空间相关知识，其中辛空间的相关概念定理均参见文献[13]。

2.1 组合设计

定义1[14]令X和B是两个不相交的有限集合，I为X与B之 间 的2 元 关 系，即X⊆X×B。D=(X,B,I)为 一个关联结构，X中的元素称为点，B中的元素称为区组，I称为关联结构。设x∈X,B∈B，若(xi,Bj)∈I， 则称点xi与 区组Bj关 联，并记作xiIBj。

当D=(X,B,I)为有限关联结构时，通常记|X|=v, |B|=b。为方便X(B)表示与一给定的区组相关联的点的集合，B(x)表示与一给定的点相关联的区组的集合，并记|X(B)|=k, |B(x)|=r。另用δ表示与两个不同的区组同时关联的点数。

定义2 令v,k,λ,t均为正整数，且v≥k ≥2,λ ≥1,t≤k。D=(X,B,I)是一个关联结构，2元组(X,B)是 一个部分平衡t−(v,k;λ,0)区组设计，如果满足下列条件：

(1) |X| = v 。

(2)对任意的B∈B, |B|=k。

(3)X的任意t元子集要么在B的0个区组中同时出现，要么在B的λ个区组中同时出现。

2.2 辛空间

对于Fq上 的2υ×2υ矩阵T，如果TKTT=K，则称T是关于K的 一个辛矩阵。显然2υ×2υ阶的辛矩阵关于矩阵的乘法构成了一个群，称为Fq上 的关于K的 2υ阶 辛群，记作S P2υ(Fq,K)， 简记为S P2υ(Fq)。

定理4Fq上 2υ维辛空间中，一给定的(m,s)型子空间中的 (m1,s1) 型子空间的数目N(m1,s1;m,s;2υ)是

3 基于辛空间的密钥预分配方案的构造

本节利用辛空间V中的( 1,0)型 子空间和( 2,1)型子空间构造一个组合设计，并基于该设计构造了一个密钥预分配方案。将整个目标区域划分为若干个大小相同的小区域，每个小区有普通节点和簇头两种类型的传感器节点，簇头的计算、存储以及通信能力都优于普通节点。同一小区内的节点或者通过它们之间的共享密钥直接通信，或者通过小区内的簇头间接通信，不同小区内的节点只能通过簇头建立通信。

3.1 部分平衡 2−设计的构造

此时X称为点集，B称为区组集。

对x∈X,B∈B， 定义x与B关 联当且仅当x⊥B。即x与B关 联当且仅当( 2,1)型 子空间x与( 1,0)型子空间B是正交的。

定理5X中任意两个不同的点或者与B中0 个区组关联，或者与 1个区组关联，即λ= 0 或 1。则(X,B) 是一个部分平衡2−(q4+q2,q2;1,0)区组设计。

证明 令x1和x2是X中任意两个不同的点，则x1和x2为V中 两 个不同 的( 2,1) 型 子 空间，并 且dim(x1+x2)=3 或4。

若dim(x1+x2)=3 ，根据2υ维辛空间中存在(m,s)型 子空间的条件，x1+x2是 一个( 3,1)型子空间。 则 (x1+x2)⊥是 一 个( 1,0)型 子 空 间， 故λ=N(1,0;1,0;4) = 1。

若dim(x1+x2)=4 ，则x1+x2是 一 个( 4,2)型子空间，(x1+x2)⊥= { 0} ，故λ= 0。

综上(X,B)是 一个部分平衡2−(q4+q2,q2;1,0)区组设计。 证毕

定理6B中任意两个不同的区组B1和B2至多与一个点同时关联。

证明令B1和B2是B中任意两个不同的区组，则B1和B2为V中两个不同的( 1,0)型子空间，且dim(B1+B2)=2 ， 同理B1+B2或 者是一个( 2,0)型子空间或者是一个( 2,1)型子空间。

如果B1+B2是 一个( 2,0)型 子空间，则(B1+B2)⊥是一个( 2,0)型 子空间，因此δ=N(2,1;2,0;4)=0。

如果B1+B2是一个( 2,1)型子空间，同样地(B1+B2)⊥是一个( 2,1) 型子空间，因此δ=N(2,1;2,1;4)=1。 证毕

由此，本文基于辛空间构造了一个组合设计，并计算了该设计的全部参数。

3.2 基于部分平衡 2−设计的密钥预分配方案的构造

将上述组合设计中的点集与密钥池中的密钥建立一一对应的关系，区组与方案中的节点建立一一对应的关系。与每个区组相关联的点数即为每个节点所能存储的最大密钥量，即密钥环的大小。密钥环即为与一给定的 ( 1,0) 型 子空间正交的( 2,1)型子空间的个数。特别地，基于该设计的密钥预分配方案中任意两个不同的节点至多有一个共享密钥。部分平衡 2−(q4+q2,q2;1,0)设计到密钥预分配方案的对应关系如表1所示。

3.3 方案设计

将整个部署区域划分为若干个大小相同的小区域，Ci表 示网络中第i个小区，每个小区包含普通节点和簇头两种类型的传感器节点。每个小区内的普通节点均采用基于部分平衡2-设计的密钥预分配方案，不同小区内节点所用密钥池各不相同，因此不同小区内的节点无法直接通信。簇头之间采用完全密钥预分配方式分发密钥，即任意两个簇头之间都有共享密钥。本方案中簇头不仅要为同一小区内两个没有共享密钥的普通节点建立间接通信，还要为不同小区内需要通信的两个节点建立间接通信。接下来介绍同一小区内普通节点与簇头如何通信，不同小区内的簇头如何通信。

3.3.1 小区内普通节点与簇头节点的通信方式

由于任意两个普通节点至多共享 1个密钥，方案的连通概率小于1。为使每个小区内没有共享密钥的两个节点也能通信，考虑利用簇头作为中间节点为没有共享密钥的两个节点建立间接通信。如何建立簇头与普通节点之间的通信是一个至关重要的问题。

基本密钥协议的主要思想是节点部署到目标区域之后，需要通信的两个节点通过密钥协商的方式建立它们之间的共享密钥。如节点Na与其通信范围内的节点Nb需 要通信时，Na从密钥列表中随机选择一个密钥ki广 播，节点Nb接 收到ki后随机产生一个密钥kij，随后将密钥kij和其身份标识符j用ki加密之后再发送给Na。节点Na将传回的信息用ki解 密之后就可得到它们之间的共享密钥kij以及身份标识信息。这样节点Na和Nb就协商了一个密钥。

本文方案中每个小区内的普通节点和簇头之间的通信采用基本密钥协议。具体方法如下：在节点部署前预先为每个簇头存储Fq(8)V中的一个1 维子空间，当同一小区内的普通节点和簇头需要通信时，这个普通节点从密钥列表中随机产生一个密钥ki并广播给簇头。由3.2节知，每个密钥与V中一个1 维子空间对应，于是簇头利用ki和 预先存储的1 维子空间生成一个2维子空间，生成的这个子空间就作为普通节点和簇头的共享密钥，记为kij。密钥kij使用ki加密之后再发送给这个普通节点，这样普通节点与簇头就可相互通信。

3.3.2 不同小区内簇头间的通信方式

每个小区内放置3个簇头，且3个簇头所用密钥池各不相同。依据所用密钥池的不同，簇头可分为3类，同类簇头可相互通信，不同类型的簇头无法通信。每个小区内的簇头用 C Hij表示，其中i表示网络中第i个 小区，j表示簇头的类型。例如C H11,CH12和C H13分别表示网络中第1个小区内的3种类型的簇头。假设目标区域被划分为N个小区，则1≤i ≤N, 1≤j ≤3，不同小区内同一类型的簇头

2 −(q4+q2,q2;1,0)部分平衡 区组设计 密钥预分配方案v =|X|=N(2,1;4)=q4+q2 密钥池大小b=|B|=N(1,0;4)=q3+q2+q+1 方案所能支持的最大传感器节点数目k =|X(B)|=N(2,1;3,1;4)=q2 密钥环大小r =|B(x)|=N(1,0;2,1;4)=q+1 包含一给定密钥的节点数目δ =0或1 任意两个节点共享的密钥量

表 1 部分平衡2−(q4+q2,q2;1,0)设计到密钥预分配方案的对应关系采用完全密钥预分配方式分发密钥，所谓完全密钥预分配即为每个簇头存储N−1个 密钥，这N−1个密钥恰好为这个簇头分别与其他N −1个小区内同类簇头的共享密钥。这样任意两个同类簇头均有共享密钥，簇头之间的连通概率为1。但随着小区数量增加，簇头存储的密钥数越来越多，对簇头的存储要求会越来越高。

基于上述考虑将每个小区的通信范围限制在其Lee球体[15]区域内。Lee距离为ρ的Lee球体是由所有与选定小区距离不超过ρ的小区组成的。任意两个小区之间的距离为这两个小区的水平距离和垂直距离之和。因此以Ci为 中心的Lee距离为ρ的Lee球体中有2ρ(ρ+1)个 小区(除Ci)，故小区内每种类型的簇头只需存储2ρ(ρ+1)个密钥。此时每个簇头存储的密钥量远少于未限制小区通信范围之前所需存储的密钥量。例如当目标区域被划分为 9个小区，且Lee距离为1时，图1实线区域为C5的Lee距离为1的Lee球体区域。

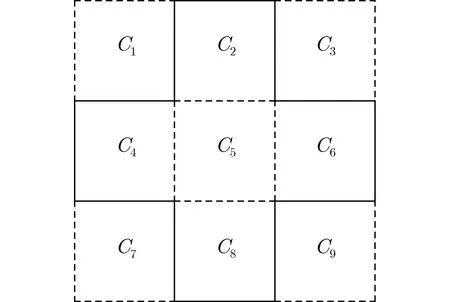
图1 ρ = 1 时C 5的Lee球体区域

4 分析

4.1 小区内的连通概率

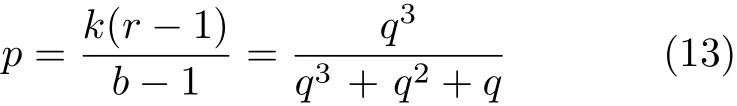
虽然这个方案的连通概率没有达到1，但是随着网络规模的不断扩大，连通概率逐渐趋于1。

4.2 损失概率的估算

网络中的节点易受敌方攻击，当一个节点被敌方捕获时，该节点内的所有密钥均被泄露。损失概率反映了网络中节点的抗捕获能力，损失概率越低，节点的抗捕获能力越强。网络的损失概率分为局部损失概率和全局损失概率。局部损失概率指一个小区内S个普通节点被捕后，任意两个未被捕获的普通节点之间链接断开的概率。全局损失概率指S′个簇头被捕后，任意两个小区之间的链接被断开的概率。

4.2.1 局部损失概率

对于任意一对给定的节点Na和Nb，假设它们之间有一个共享密钥k。由于密钥k存储在r个节点中，捕获除Na和Nb外 其余r−2个节点中的任意一个都会使密钥k泄露，此时节点Na和Nb之间的链接被破坏。 fail(1)为随机捕获一个节点，使得节点Na和Nb之间的链接被破坏的概率。于是

图2为不同网络规模下(q取不同值时)，随着捕获的节点数量逐渐增多，网络的损失概率逐渐增大。且捕获相同数量的节点时，网络规模越大，损失概率越小。

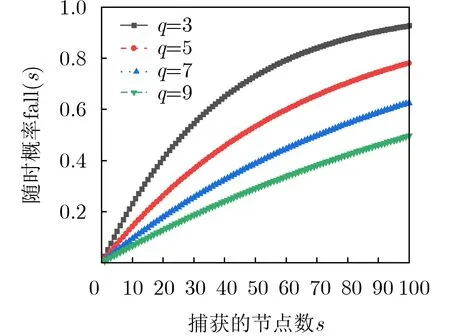
图2 损失概率图

假设一共有S个普通节点被捕获，当目标区域被划分为N个小区时，平均每个小区内有S/N个普通节点被捕获，于是局部损失概率大致估算为

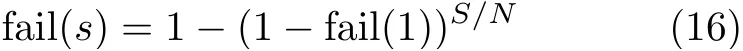
由表2可知，当捕获节点数量较多时，网络中的节点仍然具有良好的抗捕获能力。这表明将整个目标区域分为若干小区的方法极大地提高了网络中节点的抗捕获能力。

表2 当q =4 , q =5 , q =7 , q =8时的局部损失概率

4.2.2 全局损失概率

同Kumar等人[6]一样将小区之间的链接称为主链接，簇头之间的链接称为2次链接。若Ci和Cj是两个不同的小区，则Ci和Cj之间存在一条主链接。假设Ci1,Ci2和Ci3是Ci中 的3个簇头，Cj1,Cj2,Cj3是Cj中的3个簇头。此时有3条2次链接，分别为Ci1和Cj1,Cj2和Cj2,Ci3和Cj3。显然2次链接的数量是主链接的3倍。在估算全局损失概率时只考虑当S′个簇头被捕时主链接的断开情况，全局损失概率数学表达式为

事毕，我侧卧在沙发上，看见月亮高高地挂在客厅落地窗的上方，地板上那片朦胧的金色月光被玻璃拉门的对扇隔档切为两半。

当把每个小区的通信范围限制在其Lee球体区域内时，靠近部署边界的小区的Lee球体区域内所包含的小区数量减少，1个小区至多关联2ρ(ρ+1)条主链接。所以整个网络中至多有Nρ(ρ+1)条主链接。事实上，1条主链接断开当且仅当这两个小区内的3条2次链接都要断开，且捕获一个簇头时至多有 2ρ(ρ+1)条 2次链接断开。当S′个簇头被捕时，可分为下列3种情况：

(1)捕获的S′个簇头中只包含其中1种类型的簇头，则有2S′ρ(ρ+1)条2次链接断开。

(2)捕获的S′个簇头中仅包含其中2种类型的簇头，若类型1簇头有X个，则有2Xρ(ρ+1)+2ρ(S′−X)(ρ+1)条2次链接断开。

(3)捕获的这S′个簇头中包含3种类型的簇头，假设类型1簇头有X个，类型2簇头有Y个，此时有2Xρ(ρ+1)+2Y ρ(ρ+1)+2ρ(S′−X −Y)(ρ+1)条2次链接断开。

只有在第3种情况发生时，才有可能将两个小区间的3条2次链接都断开，才有可能断开1条主链接。实际中无法确定捕获的簇头包含几种类型及每种类型的簇头被捕获的数量，因此无法得到全局损失概率的理论值。但依据簇头所采用的密钥预分配方案，未被捕获的簇头之间的链接不会被断开，故簇头之间的损失概率是极小的。

4.3 节点断开的估算

当捕获的节点数量足够多时，存在未被捕获的节点所含密钥泄露的情况。此时该节点不能再使用， 这类节点称为从网络中断开的节点。考虑至少捕获多少普通节点才能从网络中断开一个未被捕获的普通节点。

因为每个节点都存储q2个密钥，并且任意两个普通节点至多共享一个密钥，因此至少要捕获q2个节点才可能断开小区内的一个普通节点。若整个网络中一共有K个普通节点被捕获，平均每个小区捕获K/N，因此需要满足K/N ≥q2， 即K≥Nq2。

例如当q= 5时 ，网络被划分为9 00个小区，则每个小区有1 56 个节点，每个节点有2 5个密钥。为了断开一个未捕获的节点至少需要捕获22500个节点。实际上，这是一个非常大的数，因此很难将一个节点从网络中断开。

由于簇头采用完全密钥预分配方式分配密钥，因此无论捕获多少簇头都不会使得未被捕获的簇头从网络中断开。

5 与一些其他方案的比较

本节将本文方案与一些其它方案就连通概率、局部损失概率进行比较。因方案设计上的差异，有些方案(除Kumar方案外)并没有区分局部损失概率和全局损失概率，因此比较时将我们方案的局部损失概率和其他方案的损失概率进行比较。图3和图4分别为连通概率和损失概率对比图，表3给出各个方案的参数。表4为符号表。

表3 各个方案的参数

表4 符号表

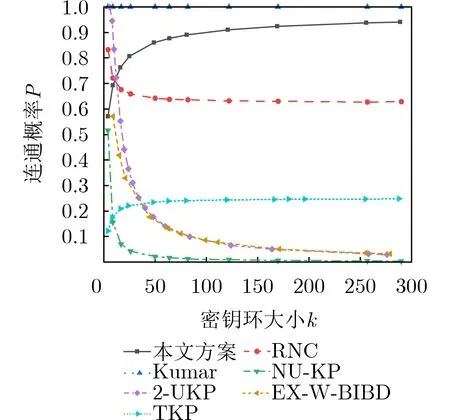
图3 连通概率对比图

Pei等人[3]基于有限域上有理正规曲线构造了一个密钥预分配方案，记为RNC。将射影空间PG(n,Fq)中 的点看作区组设计中的点集，PG(n,Fq)中所有有理正规曲线作为区组集构造了一个强部分平衡设计。当n= 2时，基于该设计下的密钥预分配方案具有良好性能。该方案的连通性随着密钥环的增大而逐渐下降，连通概率劣于本文方案，且随着节点捕获数量的增加，损失概率逐渐趋于1，远高于我们方案的损失概率。

Kumar等人[6]利用对称设计构造了一个密钥预分配方案，也将部署区域划分为若干个大小相同的小区。虽然方案的连通概率恒为1，优于我们的方案，但由图4可知捕获相同数量的普通节点时，该方案的局部损失概率高于我们方案的局部损失概率。且由于该方案簇头之间采用基于对称设计的密钥预分配方案，因此当捕获足够多的簇头时存在未被捕获的簇头从网络中断开的情况，而本文方案无论捕获多少簇头均不会有这种情况。

Bechkit等人[16]基于一种组合设计构造了一个密钥预分配方案，记作NU-KP。由于该方案连通概率较低。于是为了提高方案的连通概率作者将该方案修改进一步提出方案t-UKP。在与t-UKP比较中取t=2。从图3和图4可看到，这两个方案的连通概率以及节点的抗捕获能力均不及本文方案。

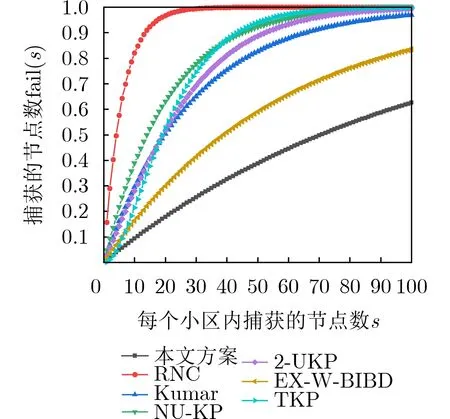
图4 损失概率对比图

袁琪等人[8]基于3维空间构造w-平衡不完全区组设计，并基于该设计构造了密钥预分配方案，记作Ex-w-BIBD。该方案连通概率较差，且损失概率也远高于本文方案的损失概率，方案的各个性能较差。

Ruj等人[17]提出了成对和三重密钥分配，该方案记作TKP。该方案中密钥链大小为k，且4≤k≤q。 方案所能支持的最大传感器数目为2q2。虽然该方案的损失概率较低，但仍然高于我们方案的损失概率，且该方案网络的连通性较差，远低于本文方案的局部连通概率。

图3为本文方案与其他几个方案在密钥环大小相近时，方案的连通概率对比图。其中各个方案的密钥环大小在4,9,16,25,49,64,81,121,169,256,289这些值上下轻微波动。图4为网络规模相近时，本文方案与其他几个方案在捕获相同节点数时，方案的局部损失概率对比图。特别地，RNC中q=4，NU-KP中q=5 ，2-UKP中q=7，Kumar方案中q=9 ，Ex-w-BIBD中q=8 ，以及TKP中q=23。从中可看到本文方案在连通概率逐渐趋于 1时还能保证较低的损失的概率。

6 结束语

本文基于有限域上辛空间中子空间之间的正交关系构造了一个新的组合设计。将目标区域划分为若干个大小相同的小区，每个小区有普通节点和簇头两种传感器节点。同一小区内的节点采用基于有限域上辛空间构造的密钥预分配方案来分配密钥，小区内的节点或者通过共享密钥直接通信，或者通过簇头间接通信。簇头之间采用完全密钥预分配方式分配密钥，不同小区内的节点必须通过簇头建立通信。

与其他方案相比本文方案既降低了网络的损失概率，又保证了在网络规模逐渐增大时网络的连通概率逐渐趋于1，即并没有以严重牺牲网络的连通概率来提高节点的抗捕获能力。此外将网络分区的方法也有效地提高了网络中节点的抗捕获能力，并降低了对方案中所能支持的最大传感器数目的要求。但本方案仍有不足之处，与其他方案相比相同规模下本文方案中每个节点存储的密钥量较多，需要进一步研究和改进。