3D密码的7轮子空间迹区分器

杨 阳 刘文豪 曾 光

(信息工程大学密码工程学院 郑州 450000)

1 引言

2008年，Nakahara[1]在CANS2008上提出3D密码。3D密码可视为3维的AES算法，将 4 ×4的字节矩阵扩展为 4×4×4，分组长度和密钥规模均为512 bit，共22轮。

3D密码设计理念新颖，对它的安全性分析自提出起持续至今。2010年王美一等人[2]提出了9轮3D密码的Square攻击，唐学海等人[3]给出了9轮不可能差分攻击，之后Nakahara[4]将不可能差分攻击提升到10轮。2012年，苏崇茂等人[5]构造出3D密码的5轮中间相遇区分器，给出了10轮中间相遇攻击，Koyama等人[6]于同年给出11轮3D密码的截断差分分析，成功率约为24%。2014年，谢作敏等人[7]给出了11轮3D密码的不可能差分攻击。2015年，任炯炯等人[8]给出了11轮3D密码的中间相遇攻击。2021年，Hou等人[9]利用3D密码的6轮yoyo区分器，给出了实际可行的7轮3D密码算法的密钥恢复攻击。

在关注对3D密码的攻击的同时，可以发现上述攻击使用的区分器轮数均小于7轮。Square攻击使用了5.25轮、6.25轮区分器，11轮3D密码的不可能差分和中间相遇攻击均构造出6轮区分器，且区分优势均为 2−504，区分3D密码与随机函数所需数据量不低于 2252.5。7轮3D密码的yoyo攻击使用了6轮yoyo区分器。为突破现有的区分器轮数，本文研究子空间迹分析方法在3D密码上的应用。

2016年，Grassi等人[10]提出了子空间迹的概念。子空间迹不强调子空间结构在轮函数下的不变性，而是表现了子空间结构在轮函数下变化的规律，进而利用具有一定规律的子空间迹建立区分器。自提出以来，子空间迹主要用于对AES,Midori等SPN密码算法的分析[11]，利用该方法在构造区分器或进行密钥恢复时，不需要S盒的具体信息。

下面描述基于子空间迹的区分器—结构区分器。

2017年文献[12]利用子空间迹，找到了AES的新性质——穷举子空间Di的全部明文对，经过5轮加密，将有固定倍数个密文对的差分属于子空间MJ(子空间Di和MJ将在第3节中定义)。将这样的“n倍”性质与明确子空间迹结合，构造出5轮AES子空间迹结构区分器。同年，Grassi[13]给出了基于AES结构区分器的混合差分攻击。2019年Boura等人[14]给出了结构区分器的构造条件。2020年，Grassi等人[15]利用子空间迹给出9轮AES-128的选择密钥区分器。2021年，Grassi等人[16]对P-SPN结构及Hades结构进行子空间迹分析并给出判断线性层是否易受攻击的工具。

子空间迹分析方法在构造区分器上有独特的优势，往往可以找到轮数更长的区分器。本文将基于子空间的性质，寻找3D密码的7轮区分器。

第2节介绍3D密码算法，定义其子空间并研究子空间传播规律；第3节证明了3D密码两个子空间交集为0，由此给出在选择明文条件下，区分优势最大的6轮3D密码差分区分器，进一步给出首个7轮3D密码的子空间迹不可能差分区分器；第4节介绍兼容、信息集、等价关系的定义及相关定理，说明了3D密码特定子空间与S层的可兼容性，据此给出3D密码的7轮结构区分器；第5节总结成果并提出开放性问题。

2 初步准备

2.1 3D密码算法

3D密码算法的分组规模和密钥规模都是512 bit，迭代轮数为22轮。分组状态表示为64 Byte的形式，可视为4个子块的联结

3D算法采用SPN结构，轮函数依次由非线性变换、行移位、列混合变换、密钥异或这4个变换组成。具体介绍如下。

非线性变换γ。使用AES的8 bit S盒。

行移位θ1, θ2。θ1是 对3D密码的4个子块做AES的行移位变换，θ2是将字节块视为一个整体进行行移位。θ1将式(1)中的状态矩阵变为

密钥异或KeyAdd。将状态矩阵与轮子密钥对应字节进行模2加运算。

密钥扩展算法与子空间迹分析无关，在此不做介绍。记Ek和Ek′分别表示奇数轮和偶数轮加密函数，旨在突出两种行移位变换，不区分圈子密钥。使用Fkm表示m轮3D密码加密函数。a加密一轮的结果为Fk(a)=π·θ·γ·KeyAdd(a)。为保证3D密码算法加脱密相似性，算法在最后一轮省略列混合变换。

2.2 3D密码的子空间与传播规律

3 3D密码的子空间迹不可能差分区分器

本节研究3D密码子空间的交集性质，寻找交集为{0}的两个子空间，构造出区分优势最大的6轮3D密码不可能差分区分器。文献[10]介绍了一种将密钥恢复攻击转化成区分器的技术，能把基于子空间迹区分器的攻击变为新区分器，从而延长区分器轮数。将这种技术应用于3D密码，首次构造出3D密码的7轮子空间迹不可能差分区分器。

3.1 3D密码子空间的交集性质及6轮子空间迹不可能差分区分器

研究子空间的交集性质对子空间迹分析有重要意义，根据迹端点的交集属性，可以得到较长迹的可预测子空间属性，原因是两个子空间的交集经过密码函数时，交集属性被保持。而交集能够降低子空间的维数，故精确地刻画一个子空间是哪些子空间的交集，并以交集的形式进行传播，能有效降低子空间经过密码函数时增长的维数，从而寻找到更长的子空间迹。先定义两个新的子空间。

结合引理2，得到3D密码的一条6轮子空间迹不可能差分

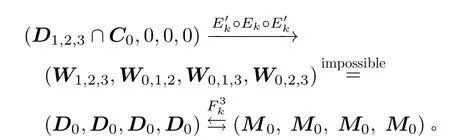
截断不可能差分区分器从终点差分矩阵脱密到中间差分矩阵，再与起始差分加密得到的中间状态产生矛盾。为延长区分器，一般终点差分矩阵只有一个变量，例如3D密码的6轮截断不可能差分区分器[7]，其区分优势为 28/2512≈2−504，与3D密码的6轮中间相遇区分器[8]区分优势相同。

而子空间迹不可能差分区分器在中间矛盾处，利用的是两个子空间交集为{0}的性质，且后几轮为明确子空间迹，维数保持不变，故终点子空间的差分变量更多。上面给出的3D密码的6轮子空间迹不可能差分区分器的区分优势为24×4×8/2512≈2−384，这是目前选择明文条件下区分优势最大的6轮3D密码区分器。

注意到，上面的子空间迹不可能差分区分器与密码规模、S盒和密钥的具体信息无关，即对带一个秘密S盒的3D密码同样有效。

3.2 3D密码的7轮子空间迹不可能差分区分器

根据2.2节给出的3D密码子空间传播规律及引理5得到一条3D密码的子空间迹

为计算区分器的数据复杂度，首先介绍“生日悖论”，寻找所需输入明文的最小数目，以保证在随机情形中以高概率产生碰撞。

给定d值和n个变量，其中至少两个变量具有相同值的概率可以计算为

下面计算该区分器所需数据量及时间复杂度。

实验数据表明，256次碰撞中有63.8%的概率得到正确密钥对应的明文对。当函数为3D密码时，修改该明文对第 0 Byte、第5 Byte以外的值并加密，不会得到碰撞。512次碰撞对应概率为87.8%。

以256次碰撞为区分界限，使用 2193.1个选择明文，将以95%的概率得到256次碰撞，有63.8%的概率将7轮3D密码与随机函数区分开。故该3D密码的7轮子空间迹不可能差分区分器的数据复杂度为2193.1个 选择明文，成功率为9 5%×63.8%=60.6%。

最后给出3D密码的7轮子空间迹不可能差分区分器的具体算法：

离线阶段。建立表格T，存储S(x)⊕02x·S(y)⊕S(z)⊕02x·S(w)=0全部解。

步骤1 随机选择明密对，检测经逆列混合变换后的密文对差分是否属于子空间(IDi, IDi, IDi, IDi)，其中i=0,1,2,3。 若无碰撞且已经使用2193.1个明密对，输出1，否则返回步骤1；若产生碰撞，进入步骤2；

步骤2 排除明文对与表格T中的解异或后的密钥值。若全部密钥被排除，输出0；否则，返回步骤1。

4 3D密码的结构区分器

第3节研究了3D密码子空间交集性质，给出了3D密码的7轮子空间迹不可能差分区分器，下面给出兼容、信息集、等价等概念的定义及相关定理，利用3 D 密码子空间与S 层的可兼容性，得到“n倍”性质并给出3D密码的7轮区分器。现有密码的结构区分器长度均不超过5轮，这是目前轮数最长的结构区分器。

4.1 兼容、信息集与等价关系

令d为S 盒操作在二元域F2上的扩张系数，Q=F2d，对于3D密码，d=8。设SPN密码作用于N个字，每个字的规模等于S盒的规模，则状态矩阵和圈密钥可表示为 QN上的向量，SPN密码的圈函数为R=K ◦L ◦S。

S是字节代替层，对状态矩阵中的比特块做非线性变换，{f0, f1,..., fN−1}为 QN一组基。

L是 QN上的一个F2- 线性双射。Q→Q。

K是轮密钥加操作，将内部状态与轮密钥异或。

定义5(兼容)[14]设V是 QN的子空间，如果V存在一组基在{f0, f1,..., fN−1}上表示为块对角矩阵时，则V与S兼容，并且称这类基为V的兼容基。

根据兼容的定义，文献[14]给出了信息集、等价关系的定义，并证明当存在与S层兼容的子空间时，密码算法有“n倍”性质，可以构造结构区分器，进一步给出结构区分器的构造条件。

根据子空间 (Mi, Mj, Ms, Mt)与S层的可兼容性，结合定理1，容易得到引理6。证明思路是交换碰撞对的某几列，得到等价消息对，结合定理1，等价消息对加密一轮差分相等，即仍然碰撞。

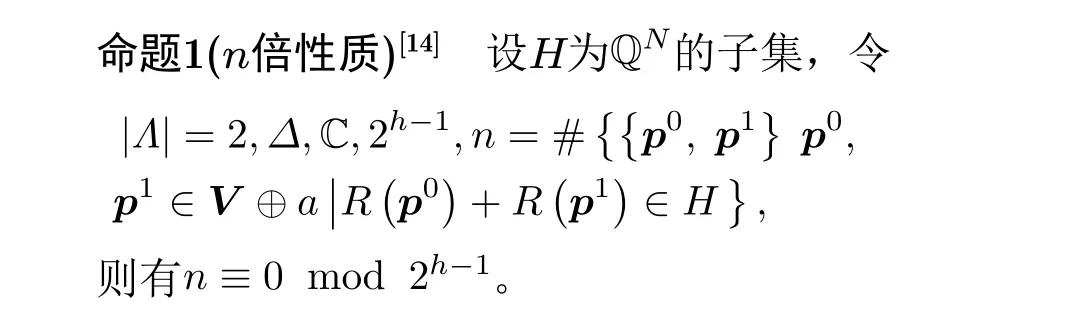
命题1说明当子空间V与S层兼容时，穷举V一个陪集中全部明文对并加密，差分属于同一子空间的密文对个数总是 2h−1的倍数，这种规律被称为密码算法的“n倍性质”。

4.2 3D密码的7轮结构区分器

以碰撞数模 215的数值作为区分依据，定理2说明穷举 (Di, Di, Di, Di)+a全部明文对，7轮3D密码得到的碰撞数模 215为0，而随机函数的碰撞数模 215为0的概率为2−15。区分成功的概率为1−2−15，大于99.99%，且利用的性质与密钥无关。需要3·2128≈2129.6次查表操作，存储复杂度为2128Byte。

5 结束语

本文对3D密码进行子空间迹分析，研究子空间传播规律，首先利用找到的3轮明确子空间迹，结合子空间的交集性质，构造了7轮3D密码的子空间迹不可能差分区分器。然后利用与S层兼容的子空间，给出了3D密码的7轮结构区分器，为基于子空间迹的攻击提供了基础。本文寻找子空间迹不可能差分区分器与结构区分器的方法，适用于任何SPN密码。

在利用子空间迹分析3D密码的过程中，发现其在寻找区分器上拥有优势。首先，截断不可能差分相比与子空间迹不可能差分，前者利用的中间相遇思想是从维数较小的终点差分矩阵脱密，在中间产生矛盾，因此区分优势较小，而后者利用的矛盾是两个子空间交集为{0}，脱密过程是一条明确子空间迹，维数保持不变，区分优势往往更大。结构区分器的原理是当输入子空间与S层兼容时，等价消息对经过一轮加密函数，差分为常数，这是SPN结构密码的新性质，但对明确子空间迹依赖很强，例如AES只有5轮结构区分器，而3D密码存在3轮明确子空间迹，故可以构造7轮结构区分器。

因此能否得到子空间迹区分器与明确子空间迹的关系，给出基于子空间迹攻击的轮数的下界是有待解决的问题。