有限区域同时同频全双工跳频自组网性能研究
2023-03-01段柏宇陈顺轲邵士海
段柏宇 陈 聪 陈顺轲 徐 强 邵士海
(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)
1 引言
无线自组织网络由于其分布式无中心和自组织协同特性,已开始应用于无人机集群、抢险救灾、安全反恐等领域[1–4]。目前,考虑到自组织网络各通信节点通信频率互相配对的需求,大多数自组网采用时分双工(Time Division Duplexing, TDD)的收发模式,节点的接收和发射不能同时进行,既增加了传输时延,又造成频谱低效使用。近年来,随着同时同频全双工技术研究的推进,通信设备在相同频带同时接收与发送数据成为可能[5]。在点对点通信中,同时同频全双工技术与TDD半双工技术相比,理论上频谱利用率最大可提升1倍[6]。但是,全双工自组网由于节点间存在互干扰以及节点自身的残余自干扰,网络容量并不会达到TDD网络的2倍[7]。
近年来,已有文献对自组网网络性能进行了初步研究。文献[8]分析了自动重传请求协议对于定向全双工自组网传输容量的影响,并与半双工网络进行了对比。文献[9]研究了单向与双向通信的毫米波自组网,指出和低频的通信网络相比,毫米波自组网可以支持更高的节点密度以及频谱效率。文献[10]分析了全双工自组网的传输容量,研究表明全双工自组网的传输容量只有在通信节点对间距离较小时,才接近半双工自组网的2倍。文献[11]同样利用传输容量,对非正交多址跳频自组网的下行链路的性能进行了分析。
上述文献主要运用传输容量指标[12–14]分析自组网网络性能,通常假设自组网网络区域无限大,节点个数无穷多;其中,节点位置分布基于随机几何模型,假设服从齐次平稳泊松点过程(Homogeneous Stationary Poisson Point Process, HSPPP),各节点位置等价,受干扰情况一致,仅分析1个节点就可推知网络整体性能。但是,现实中网络区域大小和节点规模都有限(不是无穷大),节点位置不等价,受干扰并不一致(非对称),所以在分析有限区域自组网,特别是小规模的自组网时,需考虑每一个节点的具体情况。
本文主要对区域有限同时同频全双工跳频自组网的网络性能进行分析,并与TDD收发模式的半双工跳频自组网对比:将网络中每对通信节点能成功传输的可达频带利用率之和,定义为网络可达频带利用率,作为衡量网络性能的指标;首先推导出区域内每一个节点在已知分布的条件下,网络可达频带利用率的闭合表达式;然后提出一种降低节点对间互干扰的节点位置优化分布方法,并且与节点均匀分布网络的可达频带利用率进行对比。通过数值仿真结果可知,有限区域全双工跳频网络的性能与频点个数、节点对间通信距离以及节点个数有关;当网络半径取定,对于同一分布,节点个数较少时,有限区域全双工自组网的可达频带利用率才接近半双工网络的2倍,当节点个数较多时,全双工网络的可达频带利用率将会降低,甚至低于半双工网络。
本文结构安排如下:第2节描述有限区域同时同频全双工跳频自组网的网络模型;第3节定义并推导网络可达频带利用率;第4节分析推导不同节点分布下的网络可达频带利用率;第5节通过仿真对网络性能进行分析;结论在第6节给出。
2 网络模型
2.1 通信网络描述
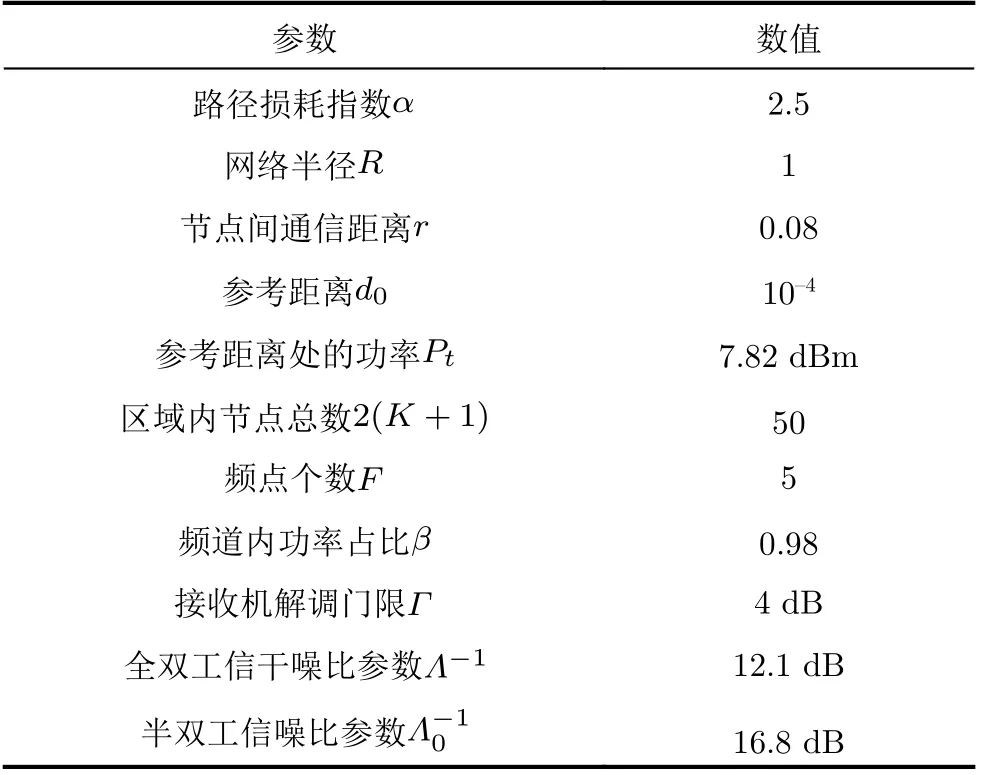
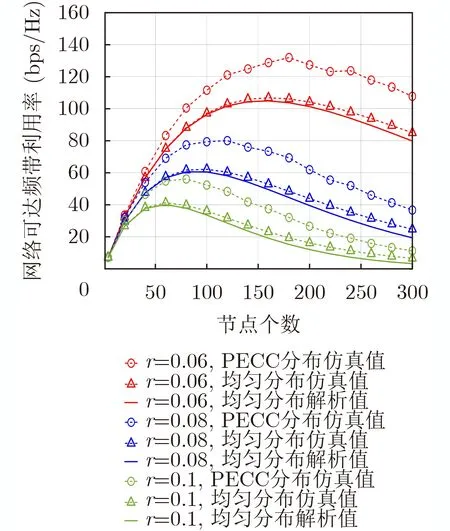
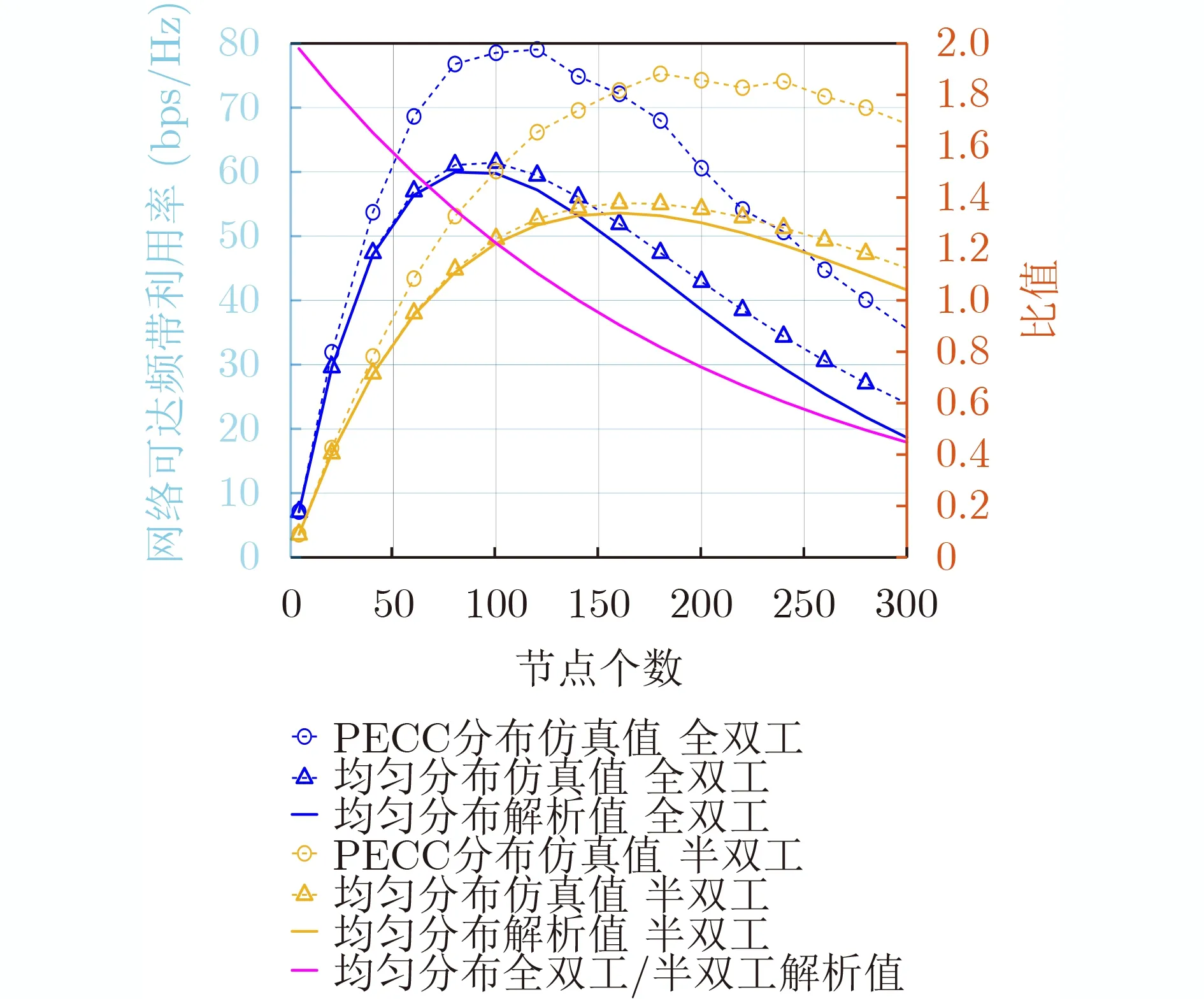
考虑图1所示的有限区域同时同频全双工跳频自组网,网络区域定为半径R的圆。网络中共2(K+1) 个节点,均分为两组:Ψα( 红)与Ψb(蓝),每组均有K+1个 节点。每个节点ak ∈Ψa均存在一个节点bk ∈Ψb与 其配对通信,其中0≤k ≤K。不失一般性,选取Ψa中任意一个节点ak记为a0,作为参考节点,与之配对的Ψb中的节点bk记为b0;每对节点ak与bk的距离记为rk,0 图1 有限区域全双跳频自组网示意图 各节点在网络区域内以一定的位置关系分布,节点对间不经过中继,直接进行同时同频全双工跳频通信。并且,每对节点独立等概地在可用频点表内选择一个频点进行通信。由于全双工设备在干扰抑制后,仍然存在残余自干扰信号[15];因此,对于网络中任意节点接收机,有两种类型的干扰:节点的残余自干扰与节点间的互干扰。 通过上节分析,参考节点a0的接收信号由期望信号、自干扰信号、互干扰信号以及噪声共4部分组成,可以表示为 其中,n(t) 表示加性高斯白噪声;s(t),w(t),I(t)分别表示期望信号、自干扰信号以及互干扰信号。假设网络中各节点发射机的发射功率均为Pt,经参考距离d0衰 减后功率为P0。 令xak(t), xbk(t)分别表示节点ak与bk的发射信号(功率归一化为1,0≤k ≤K)。传输信道考虑大尺度路径损耗与小尺度平坦衰落。 2.2.1 自干扰信号 首先分析参考节点a0的 自干扰信号w(t)。对于同时同频全双工系统,发射机以功率Pt进行信号发射时,发射信号会干扰位于同一通信节点处的接收机,因此接收机需要进行自干扰抑制。令ρ表示自干扰抑制系数(残余自干扰功率与发射功率比值),参考节点a0处经干扰抑制后的残余自干扰信号可以表示为 2.2.2 互干扰信号 2.2.3 期望信号 参考节点a0处的期望信号s(t)可以写为 由于位置不等价,每一个节点受到的干扰不同,在有限区域网络中,需要考虑每一个节点的情况。定义有限区域全双工自组织网络的可达频带利用率为 其中,Γ为接收机的解调门限,本文假设各节点接收机解调门限相等,qn为网络中各个节点的中断概率,是节点间通信失败的概率。中断概率定义为接收机处,信干噪比(Signal to Interference plus Noise Ratio, SINR)小于解调门限Γ的概率,即qn=Pr(SINRn<Γ) , 其中S INRn是网络中各节点接收机处的SINR。对于单个接收机,其信干噪比大于门限时,表示节点成功接收信号,概率为1−qn,此时可达频带利用率为l og2(1+Γ);当接收机信干噪比小于门限时,概率为qn,此时可达频带利用率为0。基于二项分布,可得出单个接收机的可达频带利用率为 ( 1−qn)log2(1+Γ)。由于网络中有 2 (K+1) 个 节点,因此CnFeDt的网络可达频带利用率是网络中各节点的可达频带利用率之和,单位为bps/Hz。因qn与SINR有关,下面给出参考节点a0处 的SINR0 其中,I表示参考节点a0功率归一化的互干扰,Lxy是各节点到参考节点的路径衰落,Λ为白噪声和残余自干扰之和与节点发射机在单位距离处功率的比值。式(10)中r表示节点bk与ak的距离,为减小计算复杂度,后续分析中每对节点bk与ak的距离rk均 设为定值r, 即rk=r,0 对于TDD半双工网络,其网络可达频带利用率与全双工类似,区别仅在于通信链路条数减半,即求和项减半,可以表示为 分析式(12),由于解调门限Γ为定值,计算网 其中,s=Γ/L00, 第3个等号成立是因为|hb0a0|2服从指数分布,最后一个等号是由于Z中I与Λ相互独立。对I的ζk求数学期望,可得 其中,第3个等式成立是因为各信道相互独立,最后一个等号利用了指数分布的性质。将式(16)代入式(14),可以得到q0|L的闭合表达式 由于参考节点a0是Ψa中任意选择的,并且对于Ψb中选择的参考节点b0, 推导也与a0一致,因此,区域内任意节点的条件中断概率均可以表示为式(17)的形式。但是,对于不同的节点,对应的干扰节点分布情况不一致,相应的Lak与Lbk不同,每一个节点的条件中断概率qn|L均需要单独计算。将qn|L代入式(12),可以得到基于节点位置分布的全双工网络可达频带利用率的闭合表达式。 对于半双工的有限区域跳频自组织网络,条件中断概率的推导类似。假设节点ak ∈Ψa为接收机,节点bk ∈Ψb为与ak配对的发射机。同样,以Ψa中任意一个节点记为a0作为参考节点,其受到发射功率归一化的互干扰IHD可以表示为 其中,Λ0=Nn/dα0P0。式(19)与文献[16]中,只考虑瑞利衰落时相似。同样,半双工网络区域内任意接收机节点的条件中断概率均可以表示为式(19)的形式,但每个节点需要单独计算条件中断概率。 若知道各节点在网络中的具体位置或者分布方式,即Lxy的具体长度或是分布已知,便可以利用条件中断概率的闭合表达式求得各节点中断概率qn,代入式(12)得到全双工网络可达频带利用率CnFeDt。 本节分析两种不同节点分布的网络可达频带利用率。一种是典型的节点均匀分布,在该种分布情况下,可以通过第3节的结论,推导出网络可达频带利用率的解析式。此外,本节将提出一种降低节点间互干扰的节点位置优化分布方法,该分布使网络具有较优的可达频带利用率。 考虑所有ak ∈Ψa在圆形网络区域内均匀分布,bk ∈Ψb在 以ak为圆心,半径为r的圆周上均匀分布。由于lak是 任意干扰节点ak到参考节点a0的距离,且参考节点a0也 是任意选择,因此lak是圆内服从均匀分布任意两点间的距离。文献[17]给出了半径为a的圆形区域内,均匀分布的任意两点间距离的概率密度函数。因为节点ak与节点bk间有固定距离r,为了使所有的bk也包含在区域为圆的网络内,节点ak应在半径为R−r的圆内均匀分布,即文献[17]中a=R −r,得 由于参考节点是任意选择的,式(22)给出的中断概率quni的解析式适用于任意一个节点,因此,节点均匀分布下的全双工网络可达频带利用率可以简化为 对于半双工网络,选择Ψa中任意一点为参考接收机a0,bk ∈Ψb为 发射机。考虑参考节点a0与干扰节点bk ∈Ψb,k ̸=0在圆形区域内均匀分布,半双工网络空间平均中断概率的解析式与全双工网络推导类似。 由于均匀分布未优化节点间的互干扰,所以希望寻找一种节点间互干扰最小的分布方式,使网络具有更高的网络可达频带利用率。接收机的SINR越大,中断概率越低,分析单个节点的SINR,当lak与lbk最 大时,互干扰I取得最小值,此时SINR取得最大值。即干扰节点离参考节点最远时,互干扰最小,SINR最大。再考虑网络整体,对于每一个节点ak ∈Ψa或bk ∈Ψb,都需要其余干扰节点距离尽可能大。因此,目标可以转化为寻找一种节点分布,使得每一对节点对之间的最小距离最大,相当于以节点对间的最大互干扰最小为准则,进行节点排布。 通常网络区域半径远大于节点对间的通信距离r,即r≪R, 我们将节点对akbk近似为在网络区域内的点nk,0≤k ≤K。这样可以将求节点对间的最小距离最大近似为求任意点之间的最小距离最大。在半径为R的圆内,求解任意点之间最小距离最大问题的数学模型可以写为:给定N≥2,在半径为R的圆盘内中放入N个点,使得任何一对点之间的最小距离最大,其中N=K+1。这个问题等价于等圆打包(Packing Equal Circles in a Circle,PECC)问题[18]:给定N≥2, 在半径为R的圆盘内放置N个半径为rc尽可能大的圆饼,圆饼间,圆饼与圆盘间互不嵌入。令(xk,yk)表 示nk在笛卡儿坐标系下的坐标,可以写出在半径为R的圆区域内,求解任意点之间最小距离最大的优化问题形式 其中,条件1表示圆饼与圆盘间互不嵌入,条件2表示圆饼之间互不嵌入。PECC问题是经典的NP难度问题,至今,人们只严格证明了N ≤11, N=19时的最优打包[18],其余N的情况只能采用近似求解的算法,通过计算机仿真找到近似解。网站www.packomania.com[19]给出了N≤2600时,通过计算机仿真解出的PECC问题圆饼半径rc及各圆饼的圆心坐标nk。 上述模型成立的基础是假设节点对akbk可以近似为在网络区域内的点nk。然而节点对间有固定的通信距离r,不能完全近似为一个点。因此需要考虑节点对akbk整体在网络区域内的分布。下面给出PECC节点分布方法,以nk为 圆心,半径r/2作圆,ak为均匀分布在该圆圆周上的一点,而bk是与ak关于nk中 心对称的另外一点,显然bk也在半径为r/2的圆周上,这样,nk将 位于ak与bk连线的中点。算法1展示了PECC分布方法的具体流程,PECC节点分布方法使得圆形网络内,任意半径为r/2圆的圆心间最小距离最大。由于节点对akbk在圆周上均匀分布,ak与bk的位置并不唯一,可通过蒙特卡罗仿真实验来计算网络可达频带利用率。 算法1 PECC节点分布方法 PECC节点分布方式由于使得任意两对节点间的距离尽量大,即节点对间的互干扰尽量小,是一种具有较高的网络可达频带利用率的有限区域自组织网节点分布方式。图2是PECC分布与均匀分布在不同通信距离r下,网络可达频带利用率的曲线。图2证明,PECC分布的可达频带利用率优于没有互干扰优化的均匀分布的可达频带利用率。本文的蒙特卡罗仿真均进行了10万次实验。 图2的仿真参数除了通信距离r,均与表1设置相同。从图2可以看出,当节点间通信距离r较大时,PECC分布的网络可达频带利用率明显大于均匀分布网络可达频带利用率。因为此时,互干扰是影响节点间通信质量的主要因素(通信距离较大,接收端期望信号功率较小),PECC分布方案是以节点间互干扰尽量小为准则进行优化,因此明显优于均匀分布。当通信节点间距离r较小时,PECC分布网络可达频带利用率和均匀分布网络可达频带利用率几乎相等。因为此时接收端的期望信号功率较大,期望信号是影响节点间通信质量的主要因素,互干扰功率明显小于期望功率,对于互干扰的优化无法有效提升网络的性能。 表1 仿真参数设置 本节通过仿真,结合前文,以网络可达频带利用率为网络性能指标,对全双工跳频自组网进行分析。表1是仿真参数设置,后文若未特别说明,均使用该表中的参数。 图3描述了在均匀分布与PECC分布下,可选频点个数对于网络性能的影响。如图3所示,在跳频频点个数较少时,增加网络中可选跳频频点个数,能明显提升网络可达频带利用率。当跳频频点个数接近或超过网络中节点个数时,增加频点个数对于网络可达频带利用率的提升很小,这是因为当频点个数足够多时,频点碰撞的概率很低。从图3也能看出,PECC分布的网络可达频带利用率要优于均匀分布的可达频带利用率。 图4是在网络区域半径R=1时,网络内节点个数与网络可达频带利用率在不同通信距离r下的关系曲线。分析图4可知,在节点个数较少时,增加节点个数可以明显提高网络可达频带利用率,但继续在网络区域内增加通信节点,由于引入了更多的互干扰,会导致网络可达频带利用率下降;减小节点对间的通信距离同样可以大幅提高网络可达频带利用率。由图4也可以看出,PECC分布的网络可达频带利用率在节点个数较少时,几乎等于均匀分布的网络可达频带利用率,当节点个数增加时,PECC分布的网络可达频带利用率将逐渐大于均匀分布的频带利用率。这也是因为随着互干扰增加,节点间的互干扰相较于期望信号,成为影响网络可达频带利用率的主要因素,PECC分布通过优化节点位置降低了互干扰的影响,这同图2所得结论一致。 图4 节点总数与网络可达频带利用率的关系 图5对比了R=1的网络有限区域全双工跳频自组网与TDD半双工跳频自组网的性能,品红色曲线表示节点均匀分布全双工网络可达频带利用率的解析值与半双工网络可达频带利用率解析值的比值。如图5所示,在有限网络区域内,全双工网络可达频带利用率并不一定优于半双工的网络可达频带利用率,甚至可能差于半双工网络。当网络区域内节点个数较少时,全双工网络的可达频带利用率大于半双工的网络可达频带利用率,不过随着节点个数的增加,可达频带利用率的比值从接近2一直下降;继续增加节点个数,全双工网络可达频带利用率甚至会低于半双工网络可达频带利用率,比值最终低于0.5。造成这种现象的原因是因为随着节点个数增加,网络中的互干扰总量增加,当节点数较少时,影响网络可达频带利用率的因素主要是通信链路的条数,由于全双工网络的通信链路条数是半双工的一倍,所以比值接近2;但当节点个数较多时,节点间互干扰成为影响网络性能的主要因素,对于每一个参考节点,全双工网络的干扰节点个数是半双工网络的2倍,因此最后的比值会在0.5左右。 图5 全双工网络与半双工网络性能对比 本文研究了同时同频全双工跳频自组网的网络性能,针对区域有限的场景下,各节点受非对称干扰的问题,定义网络可达频带利用率对网络性能进行分析,推导出节点位置分布条件下的网络可达频带利用率闭合表达式;给出圆形网络区域内,节点均匀分布的网络可达频带利用率解析式;并提出了一种降低网络节点间互干扰的PECC节点位置优化分布方法。 数值仿真结果表明,本文所提基于PECC节点分布方法在节点个数较多或节点对间通信距离较大时,相较于节点均匀分布的网络,能明显提高网络可达频带利用率。对于区域确定的跳频自组网,增加频点个数,减小节点对间通信距离以及选择合适的节点个数均可以提高网络可达频带利用率。并且,当网络区域固定,全双工网络的可达频带利用率只有在节点数较少的情况下接近半双工网络的两倍,随着节点个数增加,全双工网络的频带利用率将接近半双工网络利用率,甚至更低,在极限情况下全双工网络利用率仅有半双工网络的1/2。因此在实际部署跳频自组织网络时,需要综合考虑频点个数、通信距离、节点个数以及节点位置分布等因素,选择合适的双工模式进行部署,以达到较优的网络性能。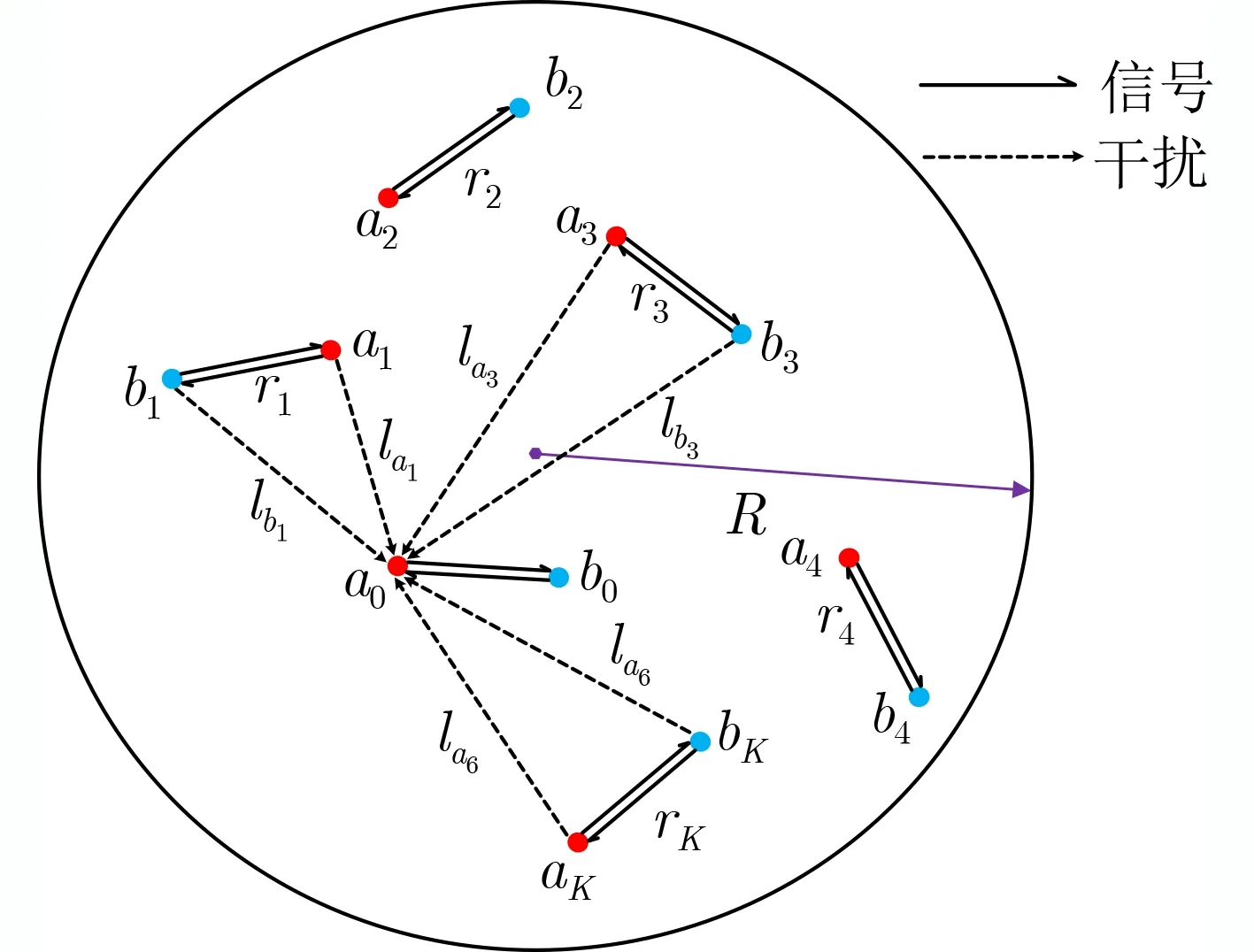
2.2 接收信号建模
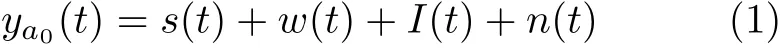
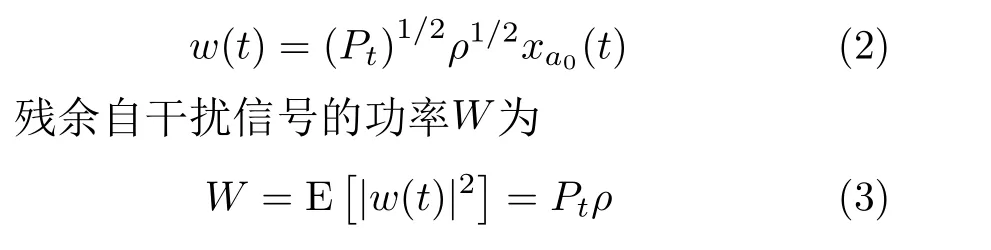


3 网络性能分析
3.1 网络可达频带利用率表征
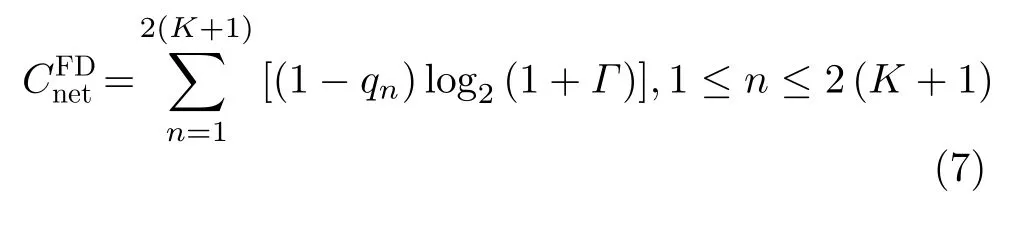

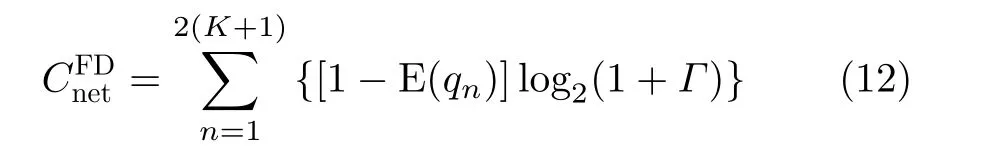

3.2 网络可达频带利用率计算


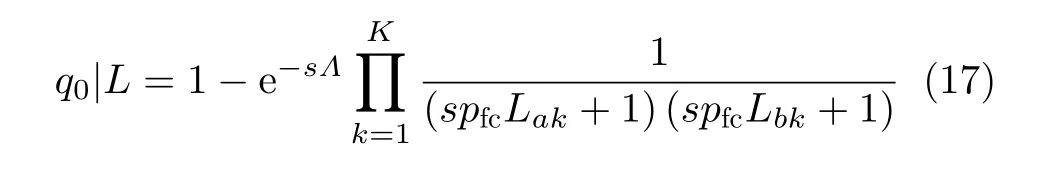

4 不同节点分布下的网络可达频带利用率
4.1 节点均匀分布



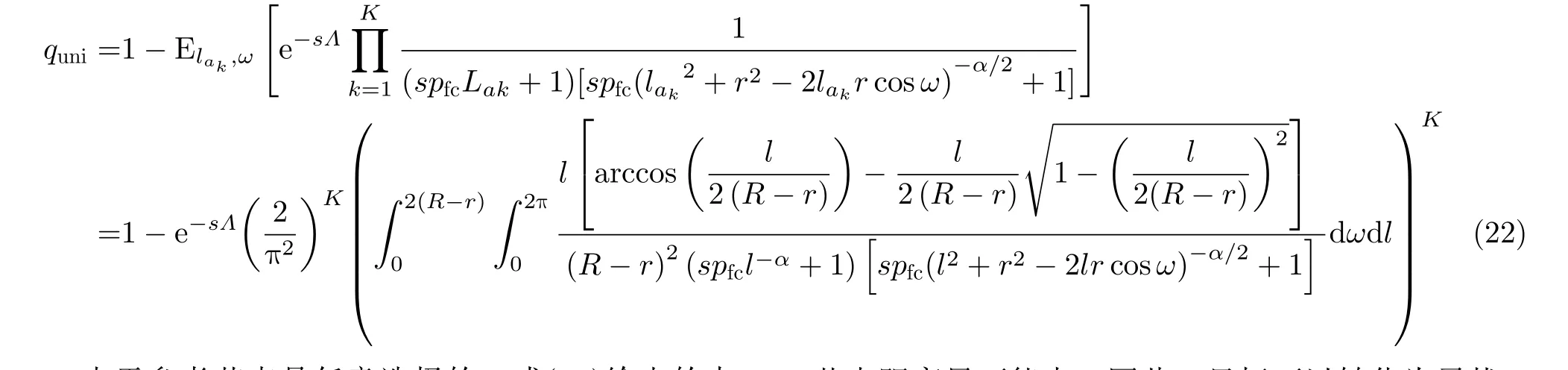

4.2 一种优化互干扰的节点分布方法
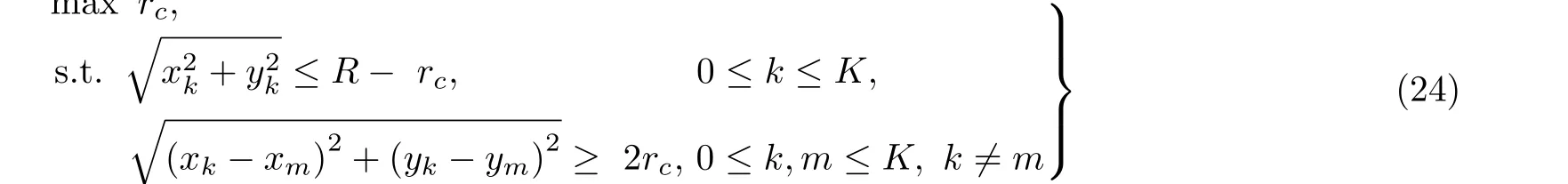

5 仿真结果与分析
6 结束语
