基于多学科优化的多用途货车白车身轻量化设计
2023-03-01韩立马春林刘莹王建勇李海鹏
韩立 马春林 刘莹 王建勇 李海鹏
(1.天津金力研汽车工程技术有限公司,天津 300384;2.中国重型汽车集团有限公司,济南 250100;3.一汽-大众汽车有限公司,长春 130011)
1 前言
多用途货车在国外汽车市场一直占据较高的市场份额。自2016年开始,国内多用途货车市场规模和渗透率不断提升。多用途货车从轻型商用货车向家商两用全能车的转型,面临能源结构替代和轻量化技术的挑战。
目前,采用全参数化建模联合多学科优化技术,实现全流程轻量化设计在乘用车领域已成熟应用[1-7],但在多用途货车领域研究尚少。本文以某多用途货车白车身为研究对象,在详细设计阶段采用多学科优化方法考量关键零件厚度,对弯扭刚度、模态频率、质量、成本进行最优化设计,深入解析非承载式白车身各设计变量对性能贡献的灵敏度,为性能优化和轻量化提供量化指标,同时为多用途货车车身轻量化评价体系提供数据支撑。
2 相关模型及试验、优化方案
2.1 多学科优化数学模型
多学科优化设计是一种考虑多种学科性能要求的综合寻优方法,通过充分探索和利用系统中多个学科的相互影响来设计复杂系统和子系统[8]。单目标有约束条件的优化问题可以表示为:
式中,X为设计变量组成的矩阵;xi为第i个设计变量;y为关于设计变量的响应;bli、bui分别为变量xi的下限和上限;n为设计变量的数量;gj(x)为第j个约束条件;BLj、BUj分别为约束条件gj(x)的下限和上限;m为约束条件的数量。
2.2 最优拉丁超立方试验设计
汽车工程领域常用的试验设计(Design of Experiment,DOE)方法有正交试验设计法、拉丁超立方试验设计法和均匀试验设计法。
最优拉丁超立方试验设计(Optimal Latin Hypercube Design,Opt LHD)改进了随机拉丁超立方设计的均匀性,使因子和响应的拟合更加精确、真实,使所有试验点尽量均匀分布在设计空间中,具有非常好的填充性和均衡性。故本文采用最优拉丁超立方试验设计法。
2.3 多项式响应面
在汽车虚拟仿真工程中,传统的有限元分析方法已经得到广泛运用,但有些仿真计算存在耗时长等问题,近似模型能够依据输入变量信息快速得到输出值,基于近似模型的优化设计被认为是解决复杂工程设计优化问题的有效途径。常采用多项式响应面法(Response Surface Method,RSM)、人工神经网络(Artificial Neural Network,ANN)、径向基函数(Radial Basis Function,RBF)、克里金(Kriging)模型等构建近似模型。
多项式响应面利用多项式函数拟合设计空间,工程上最常用的是二阶多项式响应面模型:
式中,z为响应面拟合量;k为设计变量的数量;β0、βi、βii、βij为待定系数。
2.4 误差分析指标
最常用的近似模型误差分析指标是决定系数(Coefficient of Determination)R2:
式中,yi为测试样本点的实际响应值;为测试样本点的代理模型预测值;yˉ为yi的平均值;ntest为测试样本数量。
R2可反映近似模型的整体精度,数值越大,模型的精度越高。
2.5 优化算法
工程领域,优化算法主要分为局部优化算法和全局优化算法。对于多峰问题,数值优化是一种局部优化算法。局部优化算法开发较早,计算效率高但无法保证优化解的全局有效性,通常用于解决凸问题和单峰优化问题。全局优化方法是一种求解复杂优化问题的方法,可以解决非凸和多峰问题,包括遗传算法、模拟退火算法、粒子群法、蚁群算法等。
3 白车身基础性能分析
3.1 模态分析
整车设计开发过程中,白车身模态分析求解的是固有频率和振型,目的是了解车身及各系统在受到外界激励时的动态响应,避免共振。利用MSC Nastran 软件Lanczons 算法提取白车身自由状态下第12 阶整体扭转模态固有频率为52.49 Hz,如图1所示。

图1 白车身扭转模态振型云图
3.2 扭转刚度分析
白车身扭转刚度直接影响车身振动、异响、门洞变形及操控极限,同时体现车身性能水平和轻量化程度。扭转刚度可以用白车身在受到路面扭转载荷作用时,前后相对扭转角度来描述。分析时约束后端悬置安装点的所有平动自由度,约束前端框架中性面下端点垂向平动自由度,在前端悬置安装点施加等大反向的集中载荷,使之产生绕X轴旋转的扭矩,大小为2 000 N·m,结果如图2所示,扭转刚度为34 485.9 N·m/(°)。

图2 白车身扭转变形云图
3.3 弯曲刚度分析
白车身弯曲刚度直接影响汽车行驶平顺性及车身与其他系统间的共振,可以用白车身受乘员舱内垂直载荷作用时门槛梁产生的变形描述。分析时约束前端悬置安装点的所有平动自由度,约束后端悬置安装点的垂向平动自由度,在门槛梁上端面中心位置,左右侧分别施加垂直向下的集中载荷,大小为1 500 N,结果如图3所示,弯曲刚度为11 947.3 N/mm。

图3 白车身弯曲变形云图
4 设计变量筛选及灵敏度分析
4.1 设计变量
设计变量在选取时可以参考以下准则:
a.选取对白车身整体性能贡献起主导作用的零件;
b.通过仿真工程经验判断关键零件;
c.选择对车身性能贡献的灵敏度有特殊辨识需求的零件;
d.左、右对称零件合并为一组设计变量;
e.设计变量选用离散型,使得每一组样本点具有工程意义和指向性。
区别于承载式车身结构,多用途货车白车身可以理解为长头车身和驾驶室结构的组合体,综合考虑其结构特性及现阶段研究的局限性,选取了46个设计变量,具体包括前轮罩、前围板、前地板、后地板、侧围、顶盖、后围7 个分总成73 个零件的厚度,如图4 所示。通过对标国内外3 款多用途货车白车身结构料厚,结合材料规格定义优化设计空间。

图4 白车身设计变量示意
4.2 试验设计
采用最优拉丁超立方试验设计方法,生成1 680个样本点的设计矩阵,用于进行弯扭刚度、模态频率、质量、成本的试验设计,如图5所示。
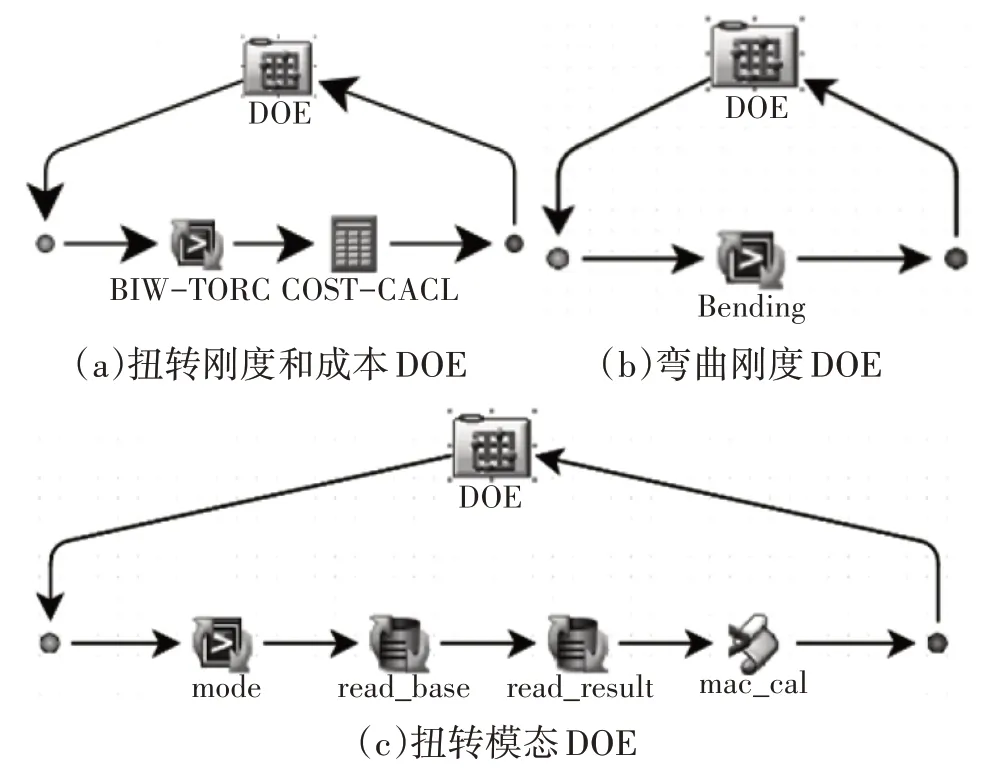
图5 弯扭刚度、模态频率、成本的试验设计流程
帕累托图(Pareto Chart)[9]反映样本拟合后模型中所有项对每个响应的贡献程度。各设计变量对扭转刚度、弯曲刚度、扭转模态的敏感程度排序如图6~图11所示。通过试验设计,可以深入理解车身结构,同时可为建立近似模型提供计算样本。
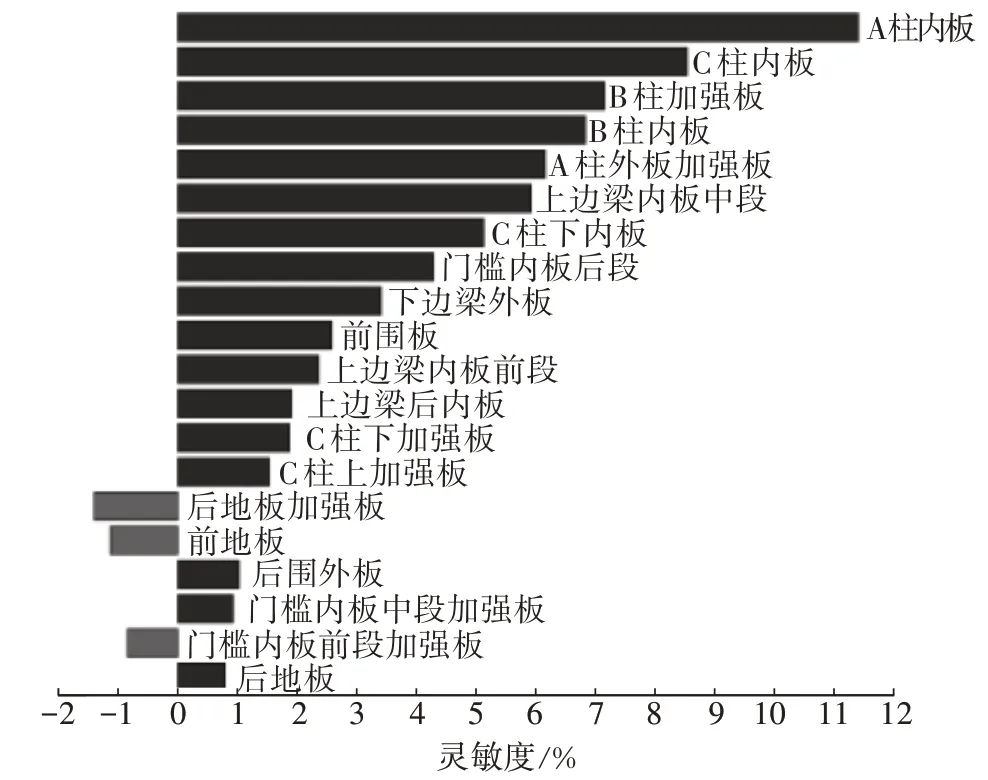
图6 白车身扭转刚度帕累托图
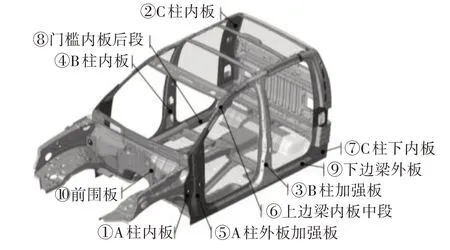
图7 扭转刚度灵敏度排名前10位的零件示意

图8 白车身弯曲刚度帕累托图
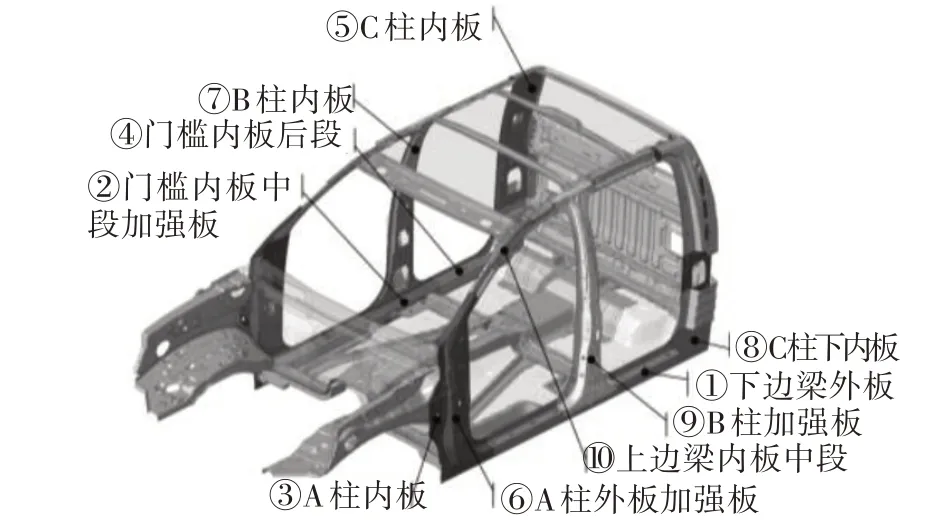
图9 弯曲刚度灵敏度排名前10位的零件示意
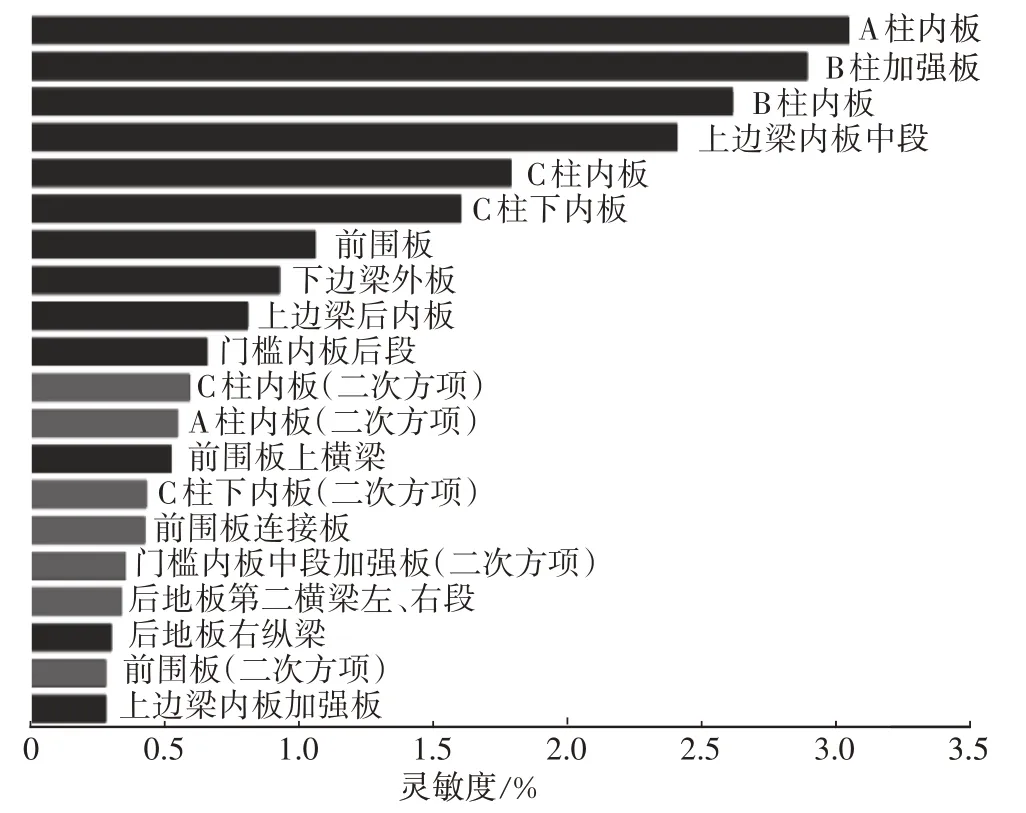
图10 白车身扭转模态帕累托图

图11 扭转模态灵敏度排名前10位的零件示意
5 零件厚度优化
5.1 近似模型
近似模型用数学表达式代替高强度有限元仿真,可减少计算次数,同时可平滑噪声,使数值优化算法能够快速找到全局解。考虑到白车身基础性能与零件厚度变量之间呈线性关系,随机抽取20个样本点,构建弯扭刚度、模态、质量、成本的二阶多项式响应面近似模型,如图12所示,误差分析结果如表1所示。

表1 白车身优化近似模型精度


图12 二阶多项式响应面近似模型
一般认为R2≥0.9时,近似模型的精度可以接受。由表1 可知:弯扭刚度、质量、成本响应的R2均接近1,说明这4个响应的近似模型能够很好地替代高强度的有限元仿真模型;模态响应的R2<0.9,其原因在于,模态分析得到的固有频率与刚度和质量有关,即设计输入(零件厚度)与模态响应(固有频率、振型、阶次)之间的线性相关性并不强。若进一步提高近似模型的精度,需要继续增加样本点数量,考虑到仿真计算效率以及除R2外的其他3个误差分析次要指标均达标,所以接受已构建的近似模型。
5.2 优化结果
通过对标车性能仿真分析,制定该多用途货车白车身整体扭转模态频率、扭转刚度、弯曲刚度的参考指标下限分别为50 Hz、15 000 N·m/(°)、7 000 N/mm。避开现阶段多用途货车白车身基础性能指标制定的局限性问题,在实施轻量化方案时以保持原车性能水平,权衡各性能的利弊来换取较大幅度轻量化效果为开展思路,具体制定依次递进的3 组优化方案,分别为:方案1,保持原车身基础性能水平;方案2,允许静刚度下降10%,扭转模态频率波动2 Hz;方案3,允许静刚度下降20%,扭转模态频率波动4 Hz。利用自动优化算法分别进行以质量最小为目标函数,刚度、模态为约束条件,成本为响应的优化设计,优化结果汇总如表2 所示。分别统计3 组优化方案中的最优解,如表3~表9所示。
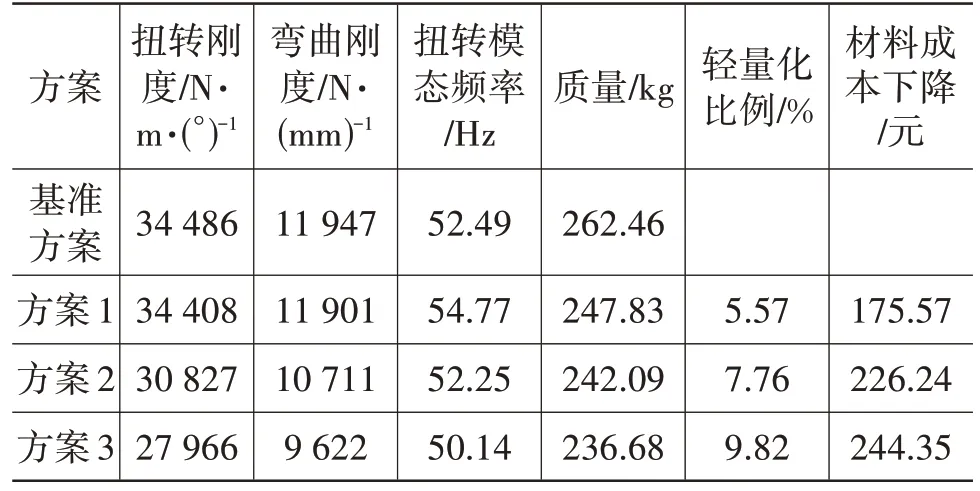
表2 3组优化方案结果汇总
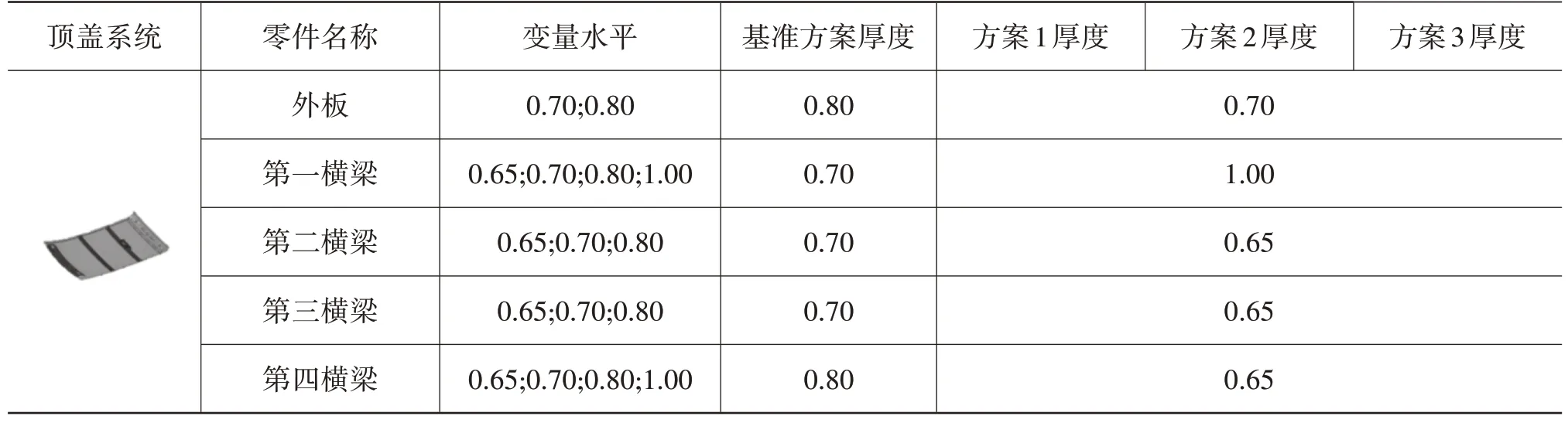
表3 顶盖优化前、后设计变量取值 mm

表4 后围优化前、后设计变量取值 mm

表5 前围优化前、后设计变量取值 mm

表6 前轮罩优化前、后设计变量取值 mm

表7 前地板优化前、后设计变量取值 mm

表8 后地板优化前、后设计变量取值 mm
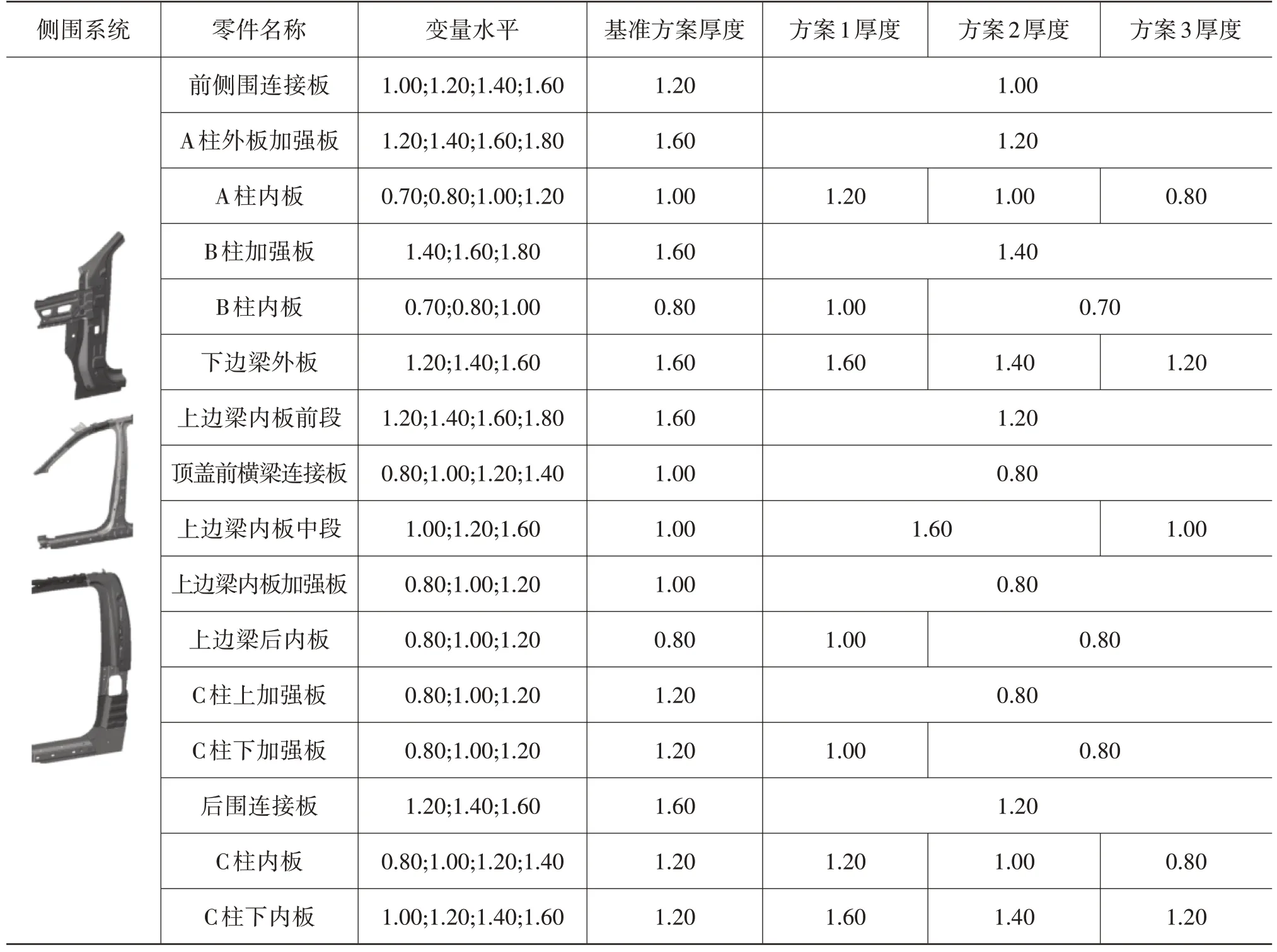
表9 侧围优化前、后设计变量取值 mm
6 结束语
本文以多用途货车为研究对象,选取车身73个零件的1 680 个样本点进行试验设计,得到各零件对性能贡献量的灵敏度排序。通过加厚敏感部件、减薄不敏感零件,实现车身板件厚度的合理设计,并采用多学科优化设计方法,从性能、质量、成本3个维度完成了对多用途货车白车身轻量化空间的研究。结果表明:以稳定现有刚度水平为目标,扭转模态频率从52.49 Hz 优化到54.77 Hz,可实现质量减轻14.63 kg,材料成本降低175.57 元;以允许刚度下降10%为目标,扭转模态与基础车身持平,可实现质量减轻20.37 kg,材料成本降低226.24 元;以允许刚度下降20%为目标,扭转模态频率较基础车身下降2.32 Hz,可实现质量减轻25.78 kg,材料成本降低244.35元。
