非球面超精密磨削误差建模与补偿研究
2023-03-01徐俊东殷跃红
徐俊东,殷跃红
(上海交通大学机械与动力工程学院,上海 200240)
0 前言
光学系统中非球面元件运用普遍,非球面元件的面形精度要求也逐步提高。面形精度是机床几何误差、热变形误差、刀具磨损误差和控制误差等因素共同产生的。为提高面形精度,通常建立机床综合误差模型,进而辨识各项误差元素并进行修正补偿。
针对机床综合误差,国内外相关学者已研究较长时间。ROSA等[1]基于小角度误差假设以及刚体运动学理论,提出三轴机床的二次型面形误差模型。KIRIDENA和FERREIRA[2]基于机构学原理建立五轴机床的空间误差模型,从而将机构学原理引入机床综合误差建模中。HAN、ZHOU[3]利用傅里叶变换原理,建立旋转轴的几何位置误差模型。K KIM、M K KIM等[4]基于刚体运动学原理,建立三轴磨床的误差精度预测模型。RAHMAN等[5]建立了准静态或静态综合误差模型,包括力变形误差以及几何误差等多种误差。杨建国[6]基于齐次坐标变换,建立车削加工热误差模型和几何误差模型。朱绍维[7]建立五轴数控铣床的面形误差模型,预测加工精度并建立补偿模型。尹韶辉等[8]研究刀具磨损误差和工件面形误差,建立补偿模型。罗松保、张建明[9]建立大深度、小口径的内凹型磨削误差模型,研究刀具安装误差对非球面磨削面形精度的影响。郭隐彪等[10]对非球面的平行磨削过程进行研究,建立误差模型并离线补偿主轴半径,提高面形精度。文献[11-14]介绍了机床几何误差的建模、测量、辨识和灵敏度分析方法,并提出多种补偿方法改善机床精度。胡摇等人[15]借鉴部分干涉原理,提出非球面误差测量的一种新方式。刘海涛等[16]研究大口径非球面加工误差,证实圆角砂轮在加工精度上更有优势。
针对大口径非球面工件加工误差的建模与补偿,国内外研究成果已相对成熟。本文作者针对小口径非球面工件,基于课题组自研的超精密磨床,采用X轴、Z轴、B轴三轴联动的斜轴磨削方式加工。基于多体系统理论,运用齐次坐标变换原理,建立综合误差模型。将综合误差集中转换为对刀误差和轮廓半径磨损误差,分别推导其传递函数、辨识误差并建立补偿模型,修正补偿误差以提高面形精度。
1 非球面超精密磨削综合误差模型
1.1 超精密磨床结构
本文作者基于多体系统理论,运用齐次坐标变换原理,建立非球面超精密磨削的综合误差模型。
图1为超精密磨床的结构示意和拓扑结构,表1为磨床各部件间存在的自由度。磨床存在两条加工运动链:刀具侧运动链为“床身0→Z轴5→B轴6→主轴7→砂轮8”;工件侧运动链为“床身0→X轴1→Y轴2→C轴3→工件4”。
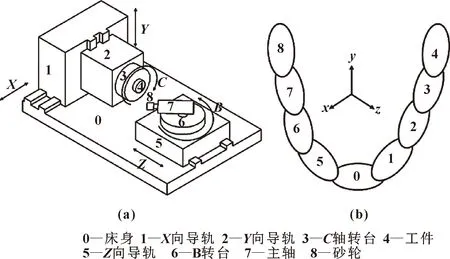
图1 超精密磨床结构示意(a)及其拓扑结构(b)
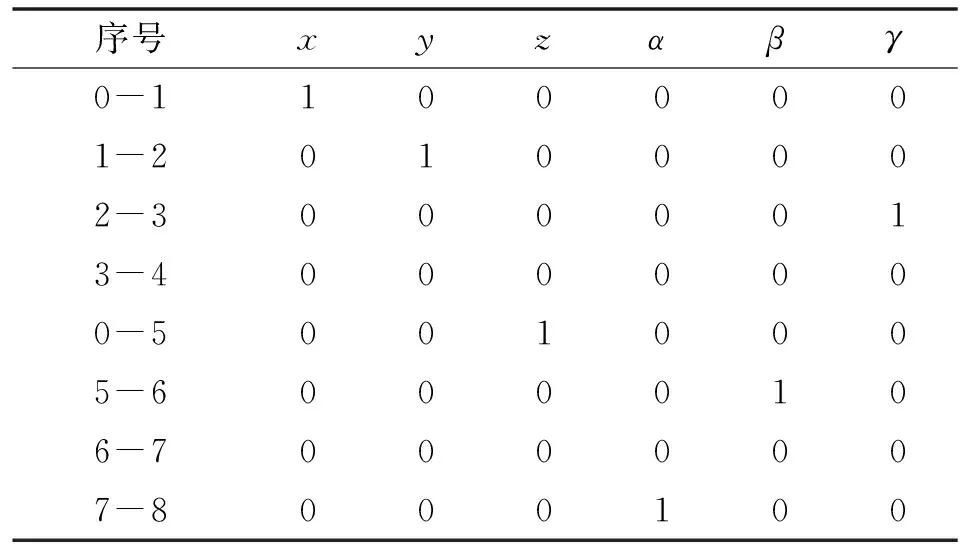
表1 各部件之间的自由度
磨削过程中,工件绕C轴旋转,砂轮绕主轴旋转的同时沿非球面母线由内向外运动。通过X、Z、B三轴联动,使得加工过程中砂轮轴线和磨削点法向量始终保持45°夹角,如图2所示。
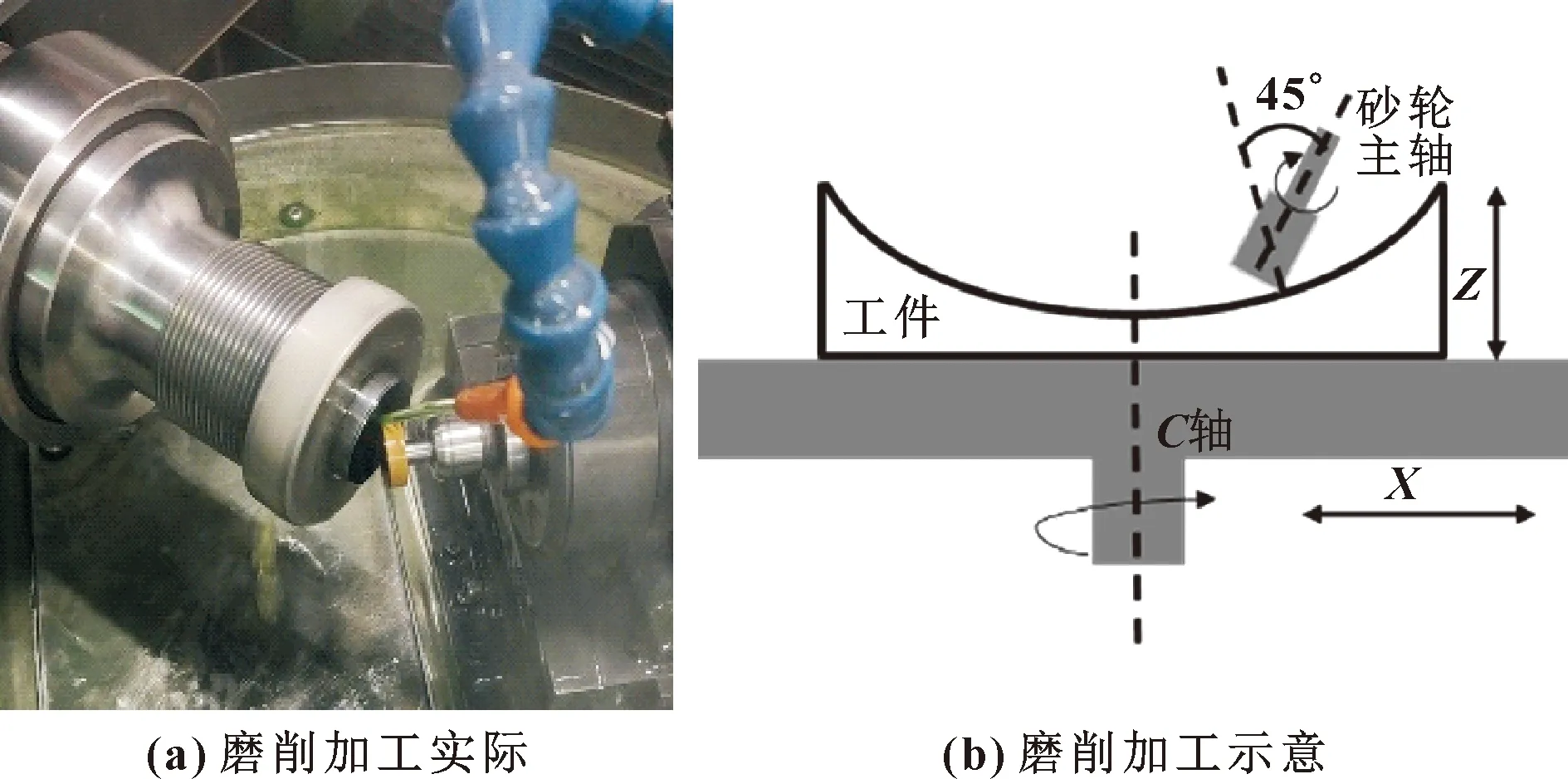
图2 超精密磨床斜轴磨削形式
1.2 非球面超精密磨削综合误差建模
每个移动轴共有6项误差元素,以X轴为例,如图3所示,分别是:1项定位几何误差δxx,2项直线度几何误差δyx、δzx和3项角偏几何误差εxx、εyx、εzx。3根移动轴之间还存在3项垂直度误差Szy、Szx、Sxy。
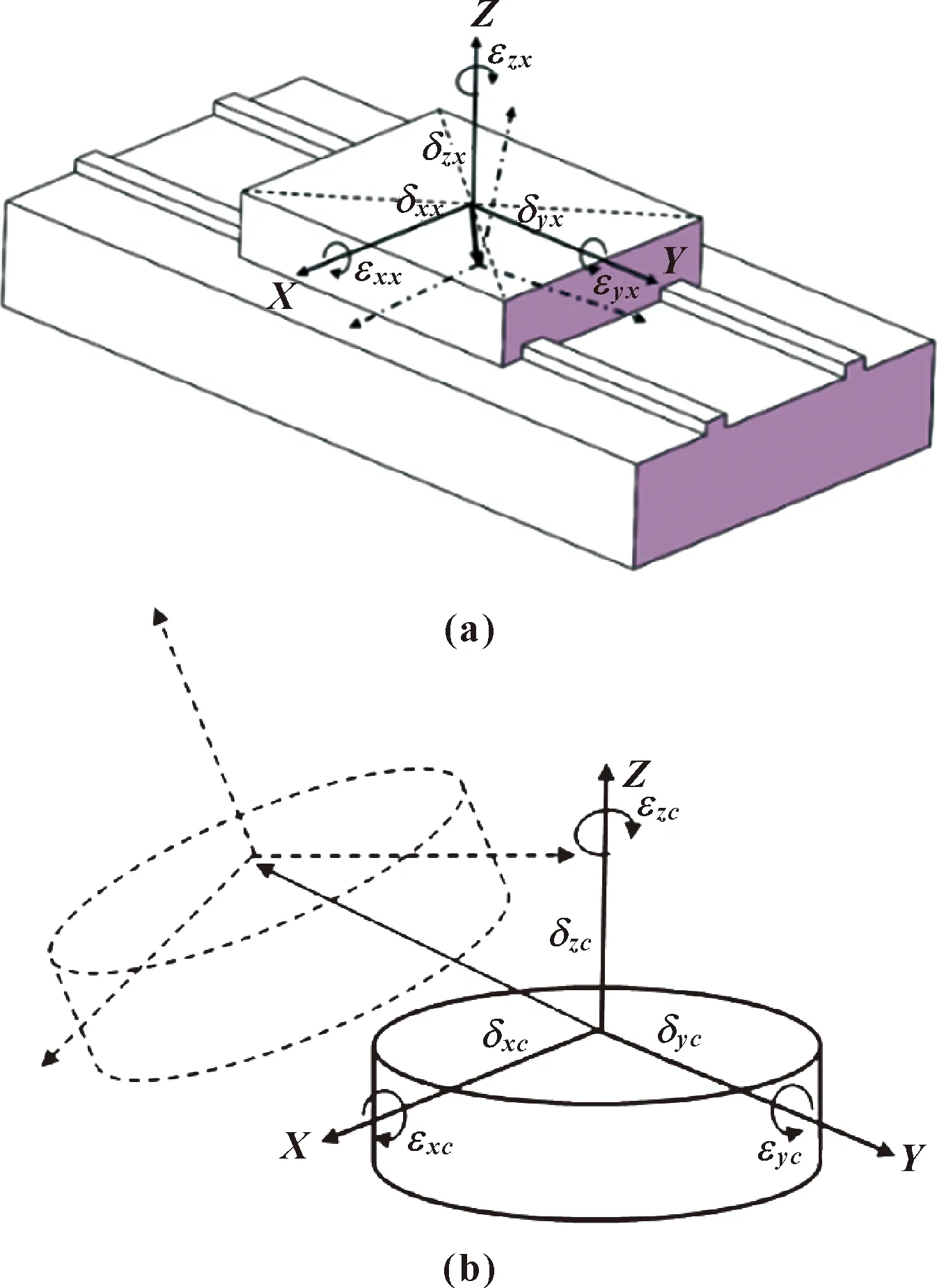
图3 移动轴(a)和旋转轴(b)误差元素
每个旋转轴包括6项误差元素,以C轴为例,分别为3项位置误差δxc、δyc、δzc,3项转角误差εxc、εyc、εzc。此外,每个旋转轴还有2个平行度误差αc、γc。
文中所涉及的磨床共3根移动轴X、Y、Z轴,两根旋转轴B轴、C轴,误差元素共37项。根据多体系统理论和齐次坐标变换原理,两运动部件之间的坐标变换矩阵可分为理想静止特征矩阵、静止误差特征矩阵、理想运动特征矩阵和运动误差特征矩阵。此外,Δα很小时,认为cos(Δα)≈1,sin(Δα)≈0。磨床各相邻体之间的坐标变换矩阵见表2。
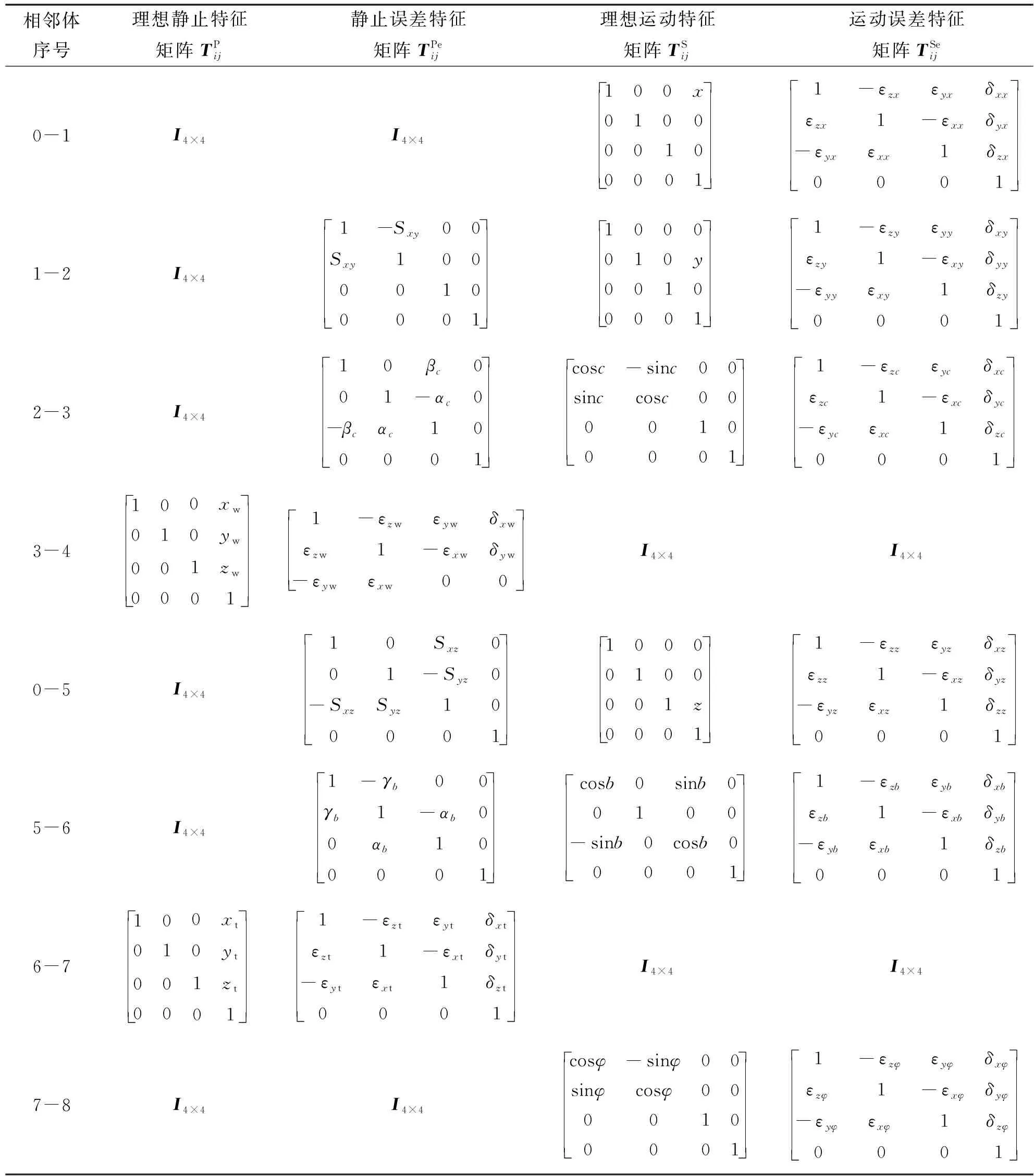
表2 磨床各零部件之间坐标变换矩阵
理想情况,工件侧运动链、刀具侧运动链分别有式(1)、式(2)的坐标变换:
PM=T01T12T23T34PW
(1)
PM=T05T56T67T78PT
(2)
联立式(1)(2)可得:
PW=(T01T12T23T34)-1T05T56T67T78PT
(3)
存在误差时,工件链、刀具链分别有式(4)、式(5):
(4)
(5)
联立式(4)、式(5)可得:
(6)
则任意点的磨削误差矢量为
(7)
该点处的法向误差近似为
(8)
式中:np为该点处的单位法向量;en为标量。
测量得到的面形误差数据不能直接用于计算,如图4所示,需要对理想曲面进行位置和角度变换,使得实际加工曲面与位姿变换后的理想曲面之间的法向误差的平方和最小。加工时工件绕C轴旋转,C轴精度较高,且与Z轴平行,因此可认为非球面磨削的面形误差关于C轴对称分布,则对理想曲面进行位姿变换近似为沿Z轴进行平移变换,平移量为d。法向误差准则函数为
(9)
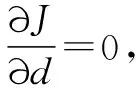
(10)
式中:(np)k为单位法向量np在Z方向分量。
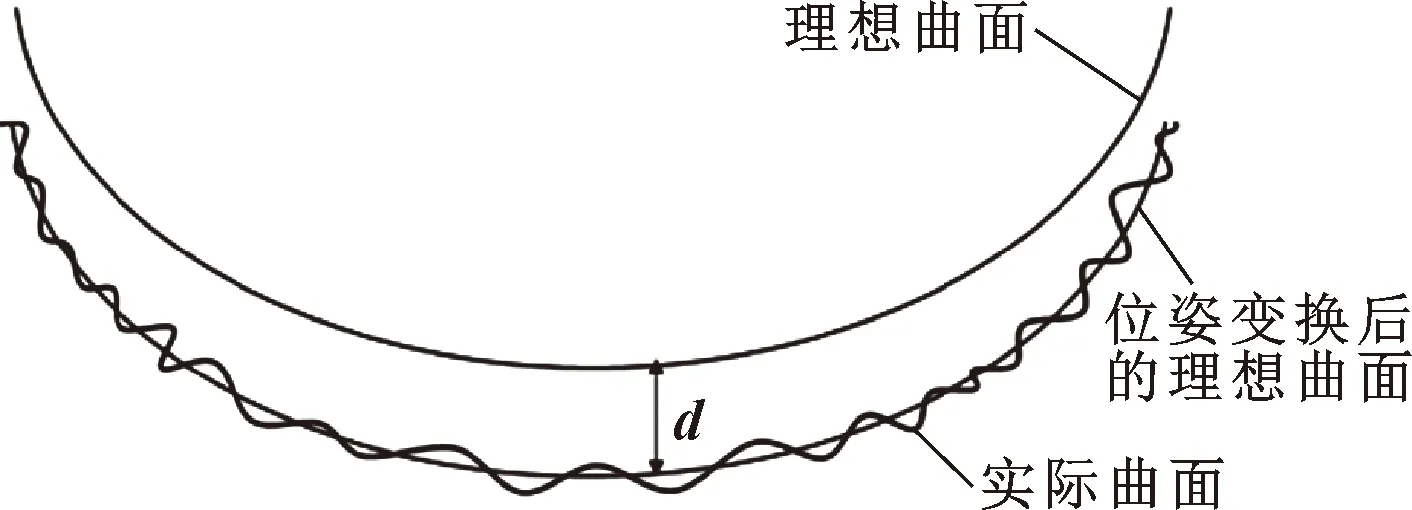
图4 理想曲面位姿变换
则任意点处法向误差大小近似计算公式为
(11)
该综合误差模型,考虑了超精密磨床各移动轴和旋转轴总共37项误差元素对综合误差的影响。
机床大部分几何误差元素通常在机床制造阶段进行标定、补偿。但是,对刀误差和砂轮轮廓半径磨损误差为磨削成形阶段产生的误差,无法预先补偿。文中取砂轮X方向的对刀误差和砂轮轮廓半径磨损误差作为主要误差来源,将其他形式引起的误差集中转换为对刀误差和砂轮轮廓半径磨损引起的误差。在辨识对刀误差和砂轮轮廓半径磨损误差后进行修正补偿。X方向的对刀误差Δx可视为磨床的相邻体6、7之间的体间静止误差,砂轮轮廓半径磨损误差ΔR可视为相邻体7、8之间的体间静止误差。根据式(7),计算得到误差矢量为
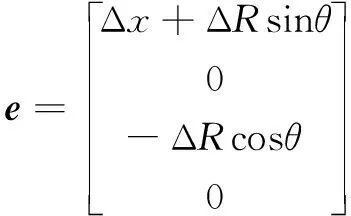
(12)
式中:θ为工件任意点处切向量和水平方向夹角。
2 误差辨识
2.1 误差传递函数
前文提到,取砂轮X方向的对刀误差Δx和砂轮轮廓半径磨损误差ΔR作为主要误差来源,将其他形式引起的误差集中转换为对刀误差和砂轮轮廓半径磨损引起的误差,辨识误差后进行修正补偿。误差辨识就是分析对刀误差和砂轮轮廓半径磨损对加工面形精度的影响,分别推导其传递函数,计算明确的对刀误差量和砂轮轮廓半径磨损量,并根据计算的[Δx,ΔR]修正补偿面形误差。
仅存在对刀误差Δx时,式(12)中ΔR=0。将式(12)代入式(10),得:
(13)
联立式(11)—(13),得到:
(14)
式中:(np)i、(np)k分别为单位法向量np在X、Z方向分量。上式表示砂轮在X方向对刀误差对各点处的法向误差的传递函数。
仅存在砂轮轮廓半径磨损误差ΔR时,式(12)中Δx=0。将式(12)代入式(10),得:
(15)
联立式(11)(12)(15),得到:
(16)
式(16)表示砂轮轮廓半径磨损误差对各点处的法向误差的传递函数。
球面工件母线方程为式(17),文中试验的非球面工件的相关参数见表3,未注明参数为0。其中工件直径为10.25 mm。
(17)
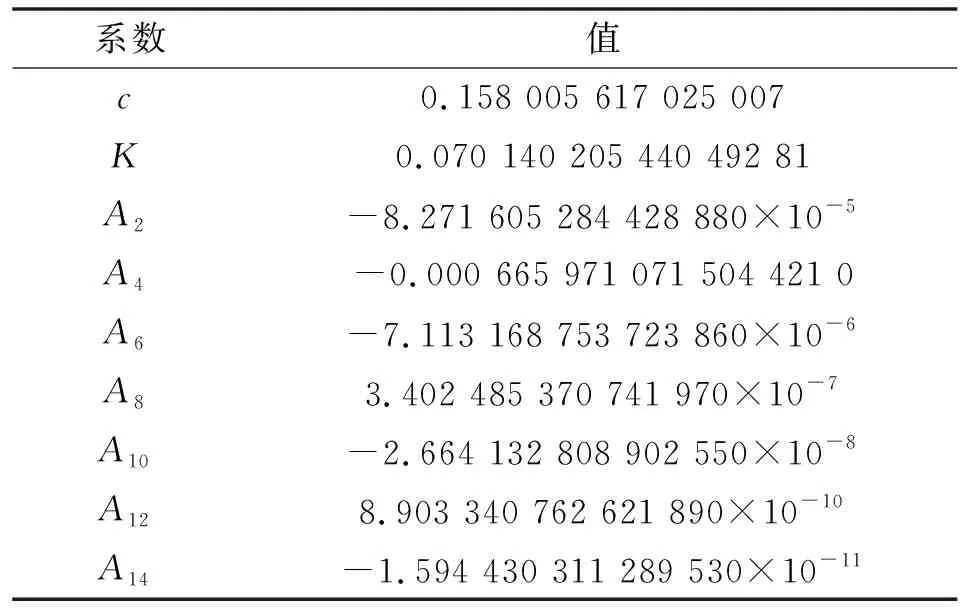
表3 非球面工件系数
根据式(14)和式(16),分别计算出X方向对刀误差和砂轮轮廓半径磨损误差对各点处的法向误差的传递函数曲线,如图5所示。
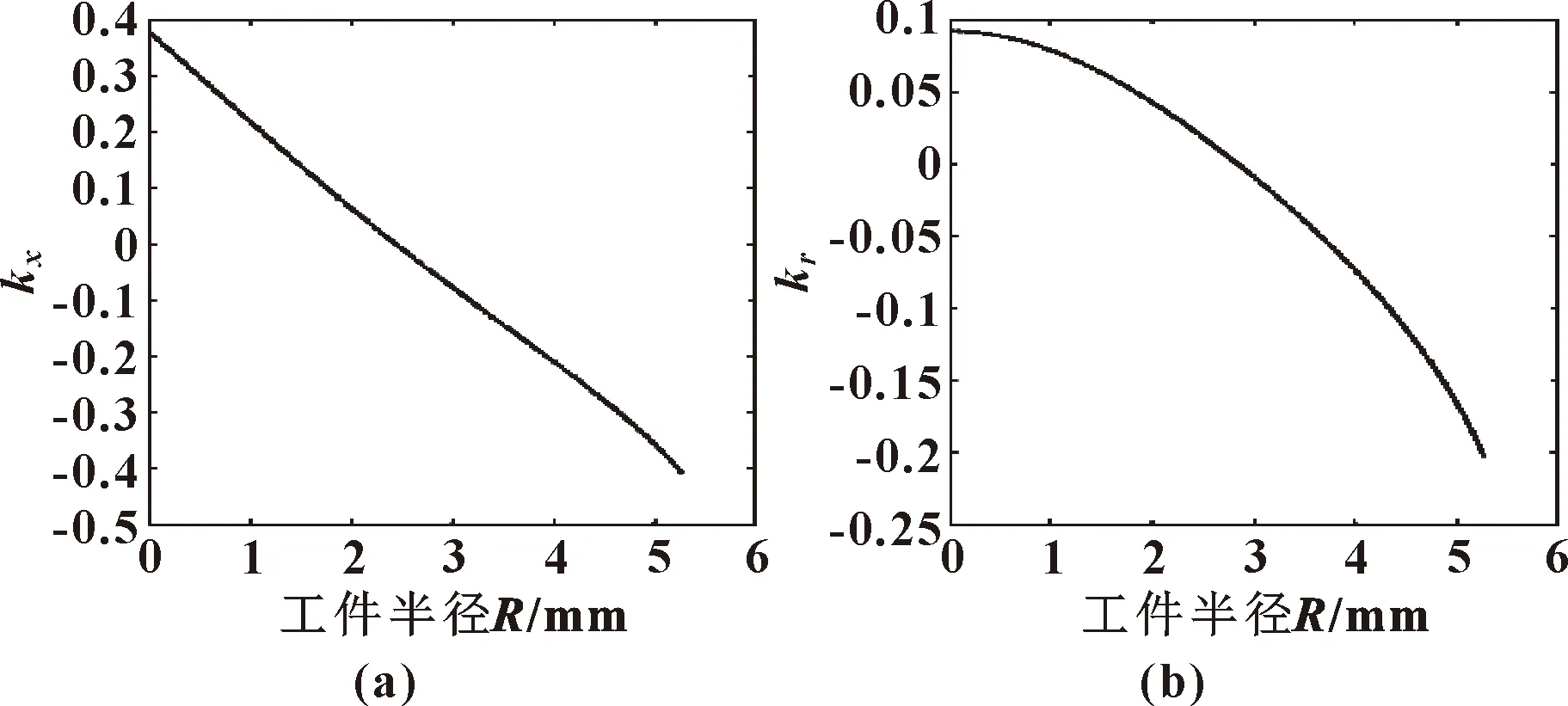
图5 kx(a)和kr(b)传递函数曲线
2.2 误差辨识算法
误差辨识之前,需要对工件的面形进行测量,得到各测量点Z轴方向误差ez。通过降噪、滤波和拟合等数据处理后,再计算每个测量点的法向误差数据en,计算方法文中不做详细阐述。根据式(11),在一阶近似的前提下,en近似为Δx、ΔR的线性组合,组合系数与非球面工件的曲面参数和测量点位置有关。分别计算每个测量点处对刀误差传递函数值kx和砂轮轮廓半径磨损误差传递函数值kr,可得下式:
(18)
通过对[Δx,ΔR]进行二维寻优,可以求解和实际测量误差曲线最匹配的误差量[Δx,ΔR]。上式是将误差集中转换到[Δx,ΔR],同时辨识[Δx,ΔR]。同理,也可以将误差集中转换到Δx或ΔR,将其中一项误差设定为某个特定值后可单独辨识另一项误差。文中通过最小二乘法求解式(18)即可求解误差值[Δx,ΔR]。辨识流程如图6所示。
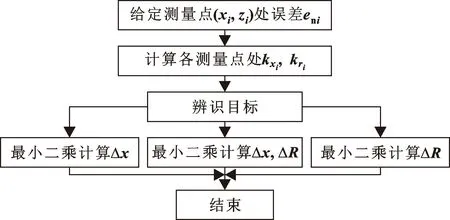
图6 误差辨识流程
3 非球面超精密磨削补偿试验
3.1 补偿试验前初加工
试验非球面工件参数见表3,使用的是盘形砂轮。对刀过程分为4步:砂轮顶点过B轴的轴线;工件轴线和C轴同轴;B轴轴线穿过工件坐标系原点;主轴轴线和C轴在Y方向同高度。
工件上被切削的点为磨削点,用Pcut表示;B轴中心为控制点,用Pctrl表示,传输给数控系统的为B轴中心轨迹在工件坐标系的一系列坐标点。
试验中,X、Z、B三轴联动。工件绕C轴以175 r/min的速度旋转,砂轮绕主轴以40 000 r/min的速度旋转,X轴方向进给的速度为0.8 mm/min。砂轮主轴固定在B轴转台上,并随B轴旋转,在磨削过程中砂轮主轴轴线和工件磨削点的法向量始终保持45°夹角。理想情况下,控制点和磨削点重合,如图7所示。
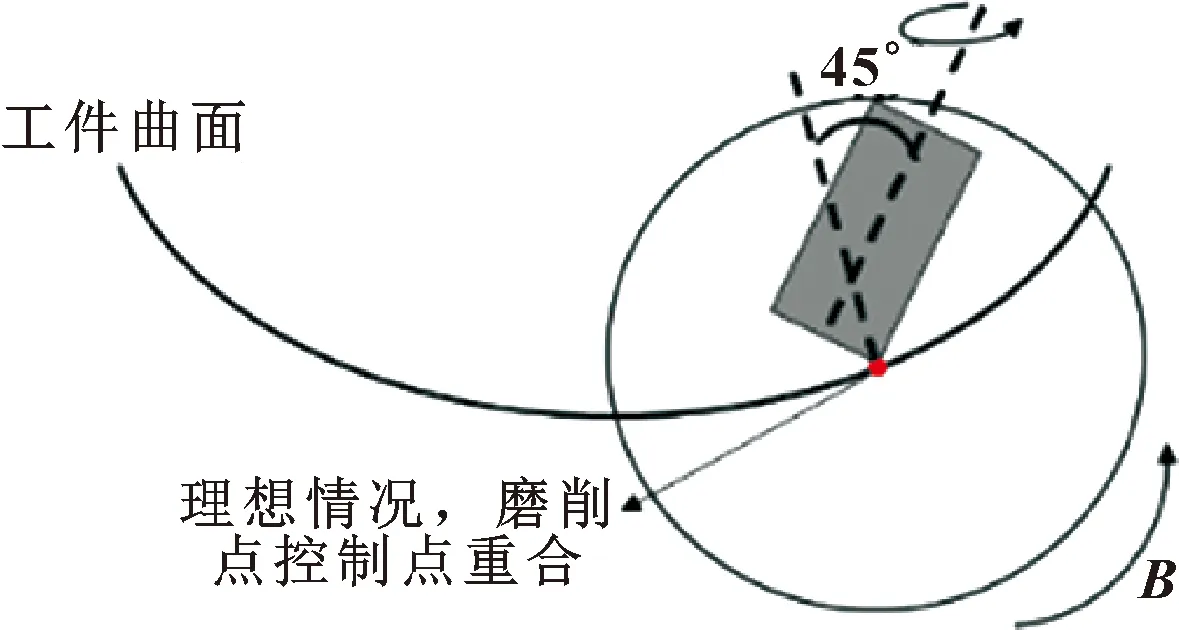
图7 理想状况下磨削点和控制点
初加工不作任何补偿,工件磨削点坐标即为控制点坐标。4次磨削深度分别为2、1.5、1、0.8 μm,磨削结束后测量工件面形误差。测得的原始面形误差如图8所示,其中面形误差的PV值为2.252 2 μm。根据文中所述综合误差模型和误差辨识方法,计算得到X方向对刀误差Δx=-4.20 μm,砂轮轮廓半径磨损误差ΔR=-4.56 μm。
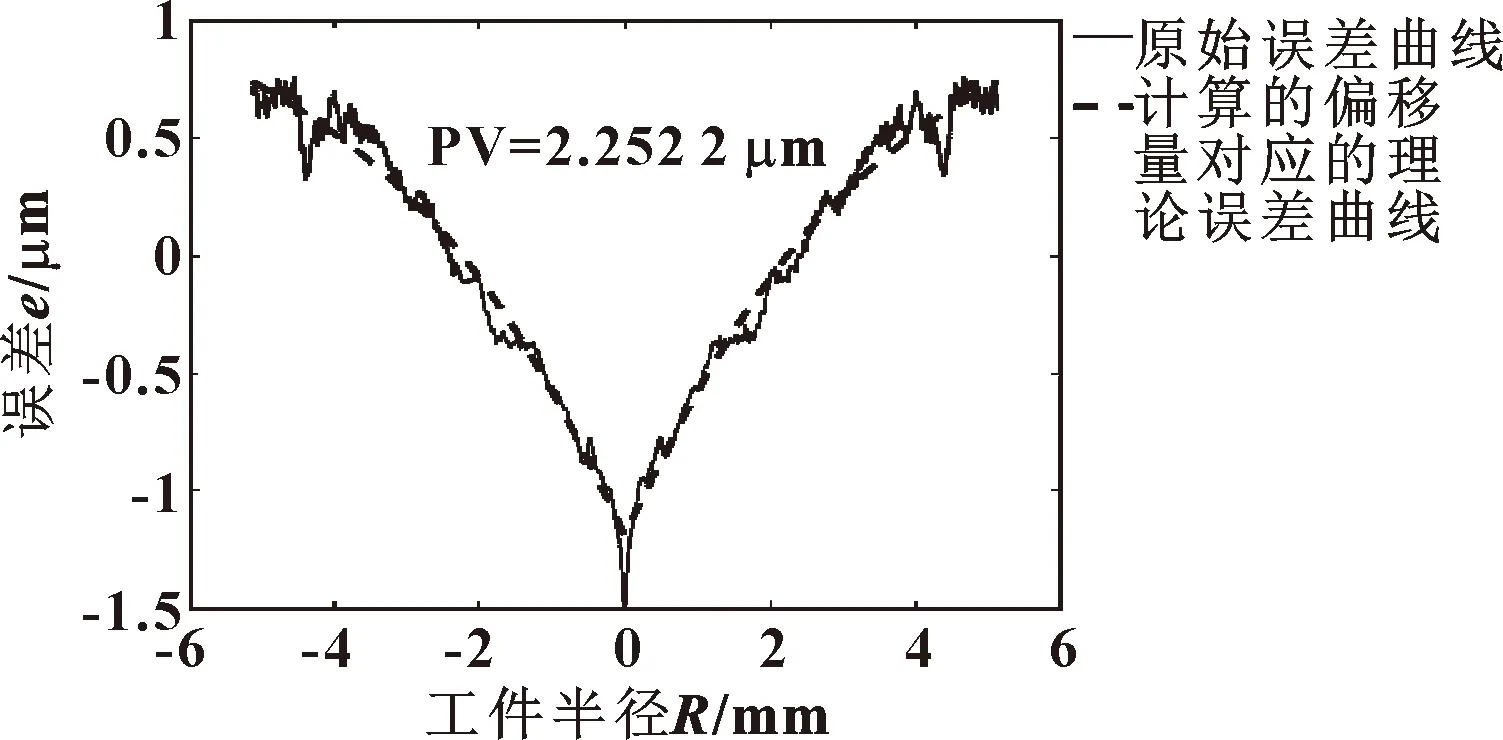
图8 初加工面形误差曲线
3.2 直接补偿法
试验中使用的是盘形砂轮,盘形砂轮的顶点为直角,相较于圆弧砂轮,本身并没有轮廓半径这项几何参数。但从图9(a)看出,此试验砂轮轮廓半径磨损误差ΔR实际上为砂轮顶点磨损量在磨削点法向量上的投影。直接补偿法即通过计算的[Δx,ΔR]修正补偿面形误差。为使得砂轮上切削点和工件上的磨削点重合,如图9(b)所示,需要将各个控制点沿着磨削点法向移动ΔR的距离。最后,再沿X轴反向移动Δx的距离。直接补偿法的修正模型为
(19)
式中:xctrl、yctrl、zctrl为控制点坐标;xcut、ycut、zcut为磨削点坐标;(np)i、(np)j、(np)k分别为磨削点的法向量np在X、Y、Z方向分量。
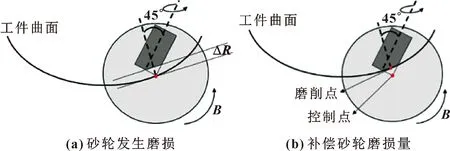
图9 磨削点和控制点
补偿量[Δx,ΔR]=[-4.20,-4.56]μm,计算控制点轨迹坐标进行补偿试验,4次磨削深度分别为2、1.5、1、0.8 μm,磨削结束后测量工件面形误差。面形误差曲线如图10所示,此时PV为0.473 6 μm。试验结果证明:相较于初始面形误差,采用直接补偿法,PV值明显降低,面形精度有效提高。
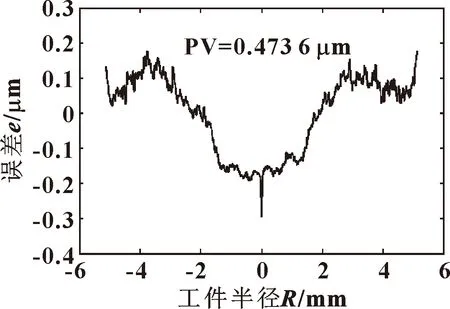
图10 直接补偿法误差曲线
3.3 基于直接补偿的点补修正法
图10结果证明:通过直接补偿法修正补偿面形误差后,非球面工件面形误差PV值明显下降,但误差曲线并不接近于水平线,且多次加工后误差也不再继续收敛。这是因为[Δx,ΔR]是通过最小二乘法计算出来的近似值,与真实值有一定差异;并且加工过程中,砂轮是动态磨损的,轮廓半径磨损误差在加工过程中并不是保持恒定的。此外,不同加工点处主轴受到的磨削力不同,主轴变形也不同。所以,仅仅补偿[Δx,ΔR],无法进一步降低PV值,提高面形精度。本文作者提出基于直接补偿的点补修正法。相较于仅仅补偿[Δx,ΔR],基于直接补偿的点补修正法是在补偿[Δx,ΔR]的基础上,结合通过降噪、滤波、拟合得到的误差曲线,计算每个磨削点处在Z轴方向的误差值ez,然后将控制点坐标的Z分量减去该误差值ez,即式(20):
(20)
采用点补修正法,结合图10的误差曲线,计算得到新的控制点轨迹坐标进行补偿试验。4次磨削深度分别为2、1.5、1、0.8 μm,磨削结束后测量工件面形误差。点补修正后的面形误差曲线见图11,此时PV值为0.097 5 μm。试验结果证明:相较于直接补偿法,采用基于直接补偿的点补修正法,面形误差曲线更加收敛于水平直线,PV值显著降低,面形精度显著提高。
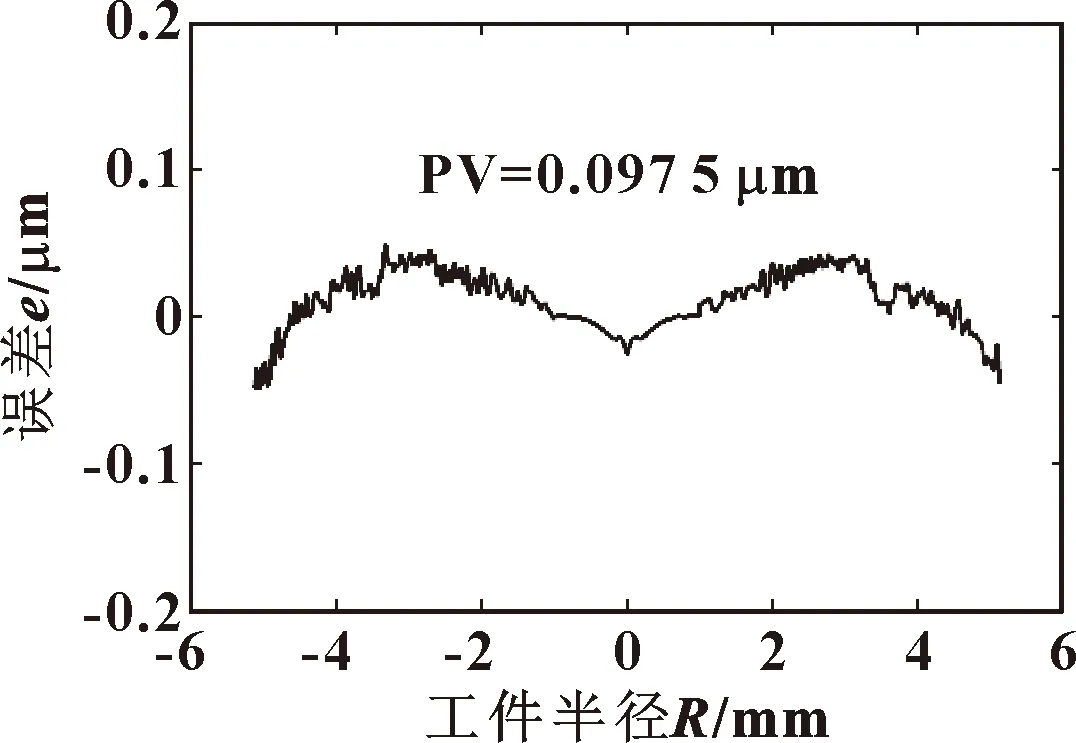
图11 基于直接补偿的点补修正法误差曲线
4 结论
(1)基于多体系统理论,运用齐次坐标变换原理,分析磨床37项几何误差来源,建立非球面超精密磨削综合误差模型。
(2)将综合误差集中转换为对刀误差和砂轮轮廓半径磨损误差,分别推导误差传递函数并辨识误差用于修正补偿。
(3)通过初始面形误差曲线辨识[Δx,ΔR],采用直接补偿法对面形误差修正补偿。试验结果表明:相比初始面形误差,PV值明显降低。直接补偿法有效提高面形精度。
(4)采用基于直接补偿的点补修正法,试验结果表明:相比直接补偿法,面形误差曲线更加收敛于水平直线,PV值显著降低。基于直接补偿的点补修正法显著提高面形精度。
