基于模型预测电流控制的伺服电机系统转矩脉动抑制研究
2023-03-01赖媛媛
赖媛媛
(新乡学院机电工程学院,河南新乡 453000)
0 前言
永磁电机是伺服控制系统的核心部分,其性能好坏将直接决定整个系统的性能。在永磁电机中,由于实际的气隙磁场分布非正弦,会导致反电动势波形中也存在相应的谐波分量,从而引起额外的转矩脉动,进而导致振动、噪声,降低系统的控制精度。因此有必要采取一定的措施对其进行抑制。
国内外学者针对永磁电机转矩脉动抑制方面的研究工作主要从电机本体和控制角度两方面进行展开。在电机本体方面,主要通过降低齿槽转矩、提高反电动势波形正弦度来实现;而在控制方面则有改进控制算法、谐波注入等。
降低电机的齿槽转矩主要是通过改变电机的设计参数以改变气隙磁导分布或改变永磁体剩磁密度的空间分布,从而达到抑制齿槽转矩的目的。具体有辅助槽、不等齿宽、不等槽宽、斜槽、优化槽口宽度[1-3]等。一般而言,虽然采用定子辅助槽能减小齿槽转矩,但是由于齿部开槽,在一定程度上会降低电机的过载能力;不等槽宽和齿宽会引起额外的不平衡磁拉力;定子斜槽会大大增加工艺复杂度。此外,在优化反电动势波形的正弦度方面,常用的方法包括磁极偏移、优化极弧系数、分段错极、永磁体削角[4-7]等。其中,采用磁极偏移的方法虽然能够有效减小齿槽转矩,但是同时也会导致电机的不平衡磁拉力;永磁体削角的方法则会增加工艺复杂度,增加加工成本。
在控制方面,为了降低电机的转矩脉动,通常采用改进控制算法或者谐波注入等。文献[8]提出一种考虑定位力矩补偿功能的模型预测转矩控制方法,认为所提控制方法不但能实现定位力矩补偿和转矩脉动抑制,还具有较好的动态性能。文献[9]则提出了一种模型预测直接转矩控制方法,认为该方法与传统直接转矩控制相比,可以有效地抑制转矩脉动,同时降低逆变器开关频率,减小开关损耗。文献[10-11]研究了永磁同步电机的模型预测电流控制,并对相应的预测进行了误差分析及抑制。文献[12]提出了一种基于特定次谐波注入法的谐波抑制方法,即在SPWM正弦信号中注入相应5次、7次谐波补偿电压,进而达到降低输出电流特定次谐波含量的目的。
本文作者首先建立了适用于任意相永磁电机反电动势谐波产生的脉动转矩通用解析模型;然后,基于此模型,从控制的角度出发,提出采用电流谐波注入以补偿反电动势谐波引起的转矩脉动控制策略,分析所需注入的电流谐波特性的一般表达式,并通过模型预测电流控制方法对电流进行控制。为验证所提出方法的有效性,以一台三相12槽10极表贴式永磁同步电机为例,通过MATLAB/Simulink设计了考虑反电动势谐波的电机仿真模型,搭建了基于谐波注入的电机控制系统。此外,为进一步验证所提方法的正确性,也进行了相应的试验验证。
1 12槽10极电机
1.1 电机结构
以一台经典的12槽10极表贴式永磁电机为研究对象,电机的横截面如图1所示,同时其相应的关键设计参数列于表1。由图1可见,在这种表贴式结构中,由于永磁体安放在气隙中,使得交直轴磁路磁阻几乎相等,因此,交直轴电感也几乎相等,该类电机通常采用“id=0”的控制策略。
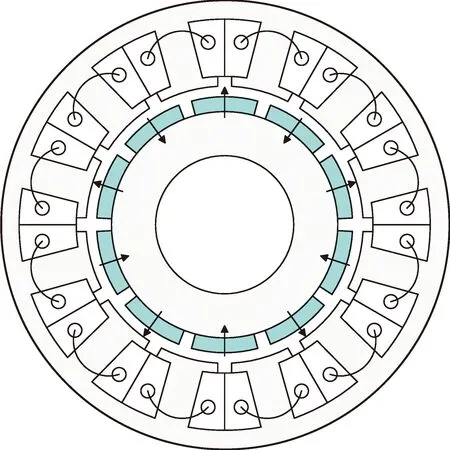
图1 传统12槽10极表面式永磁电机
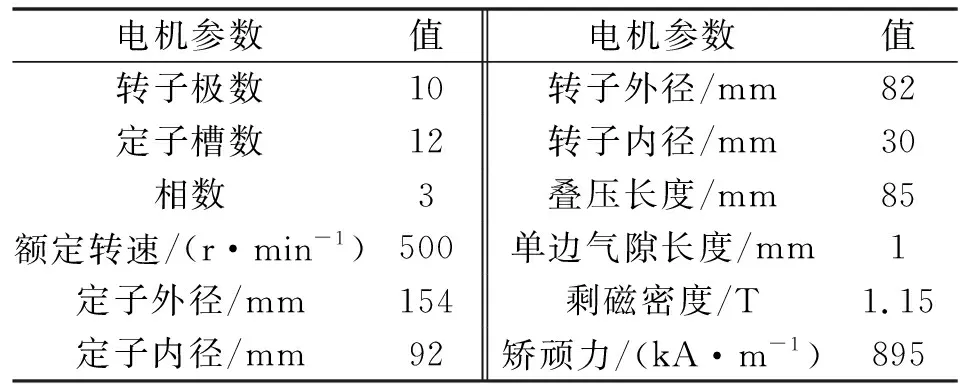
表1 关键设计参数Tab.1 Key design parameters
1.2 反电动势
一般而言,对于任意具有m相的永磁电机而言,其空载反电动势的表达式为
(1)
式中:Ev为v次谐波幅值;ω为电角速度;t为时间;γv为相位,m为相数。
因此,通过有限元仿真计算得到图1所示的3相12槽10极永磁电机的空载反电动势仿真波形为图2(a)所示,相应的谐波分析如图2(b)所示。可以看到:该电机反电动势波形中,除了基波之外,还有较大幅值的3次和5次谐波。其中3次谐波不产生转矩脉动,而5次谐波则会引起转矩脉动,因此,为提高系统的控制精度,有必要将其进行抑制。接下来将会详细进行阐述。
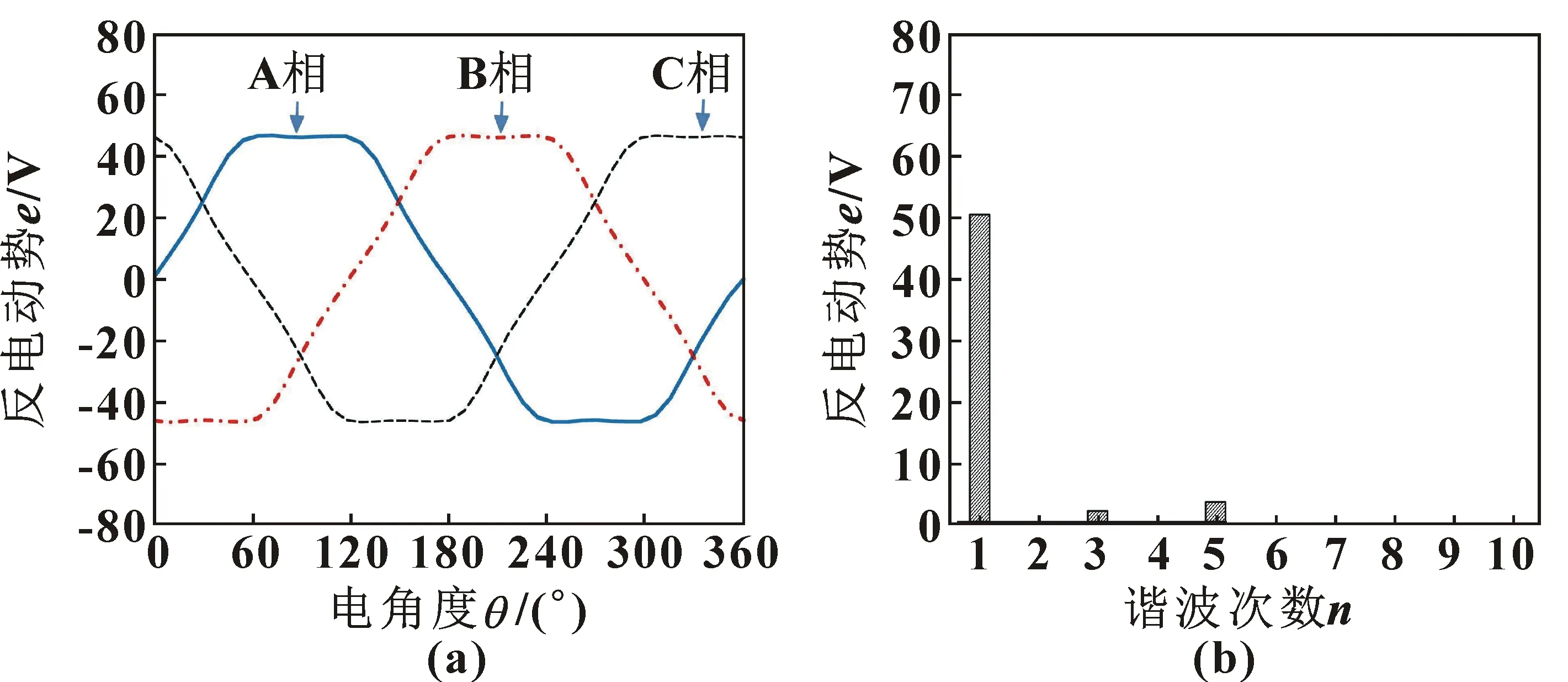
图2 反电动势(a)及其谐波分析(b)
1.3 转矩脉动产生机制
首先推导了适用于任意相电机反电动势谐波引起的转矩脉动的解析表达式;然后,基于此模型,分析所需注入的每相电流谐波特性。
通常,对于任意一台m相永磁电机而言,其永磁转矩可表示为
φμ],且|μ±v|=mk,k=0,1,2,…
(2)
因此,根据公式(2),便很容易得到基波电流与v次反电动势谐波作用产生的脉动转矩,即公式(3):
且|1±v|=mk,k=0,1,2,…
(3)
因此,如果采用注入μ次谐波电流以补偿v次反电动势谐波作用产生的脉动转矩(忽略反电动势高次谐波与μ次谐波电流之间的相互作用),则有:
且|μ±1|=mk,k=0,1,2,…
(4)
此外,所注入的谐波电流也必须同时满足以下条件:
(5)
因此,所需注入的谐波电流特性可由公式(5)求得,包括相应的幅值、谐波次数和相位。
2 数学模型
2.1 dq坐标系中的数学模型
在dq坐标系中,永磁电机的电流和磁链方程可分别由公式(6)和(7)进行表示:
(6)
(7)
式中:id、iq、ud、uq、Ld、Lq、ψd和ψq分别为直轴电流、交轴电流、直轴电压、交轴电压、直轴电感、交轴电感、直轴磁链和交轴磁链;Rs为定子电阻;ψpm为永磁磁链。
而电机的转矩模型则可表示为
(8)
2.2 预测模型
首先,需要根据公式(9)对电机的数学模型进行离散化[11],通常采用的方法是用一阶差商代替一阶导数,即:
(9)
式中:tk+1-tk为时间步长,可用h表示;k和k+1分别为第k次和第k+1次采样。
将上式代入到式(6)—式(8)中,可分别得到:
(10)
(11)
(12)
3 基于谐波注入的控制系统仿真研究
3.1 控制系统原理
图3为基于谐波注入的永磁电机模型预测电流控制原理框图,包括电机模块、电流预测模型、谐波电流注入模块、模型预测控制器以及逆变器等模块。以12槽10极永磁电机为例,电机的关键参数已在表1中给出。

图3 控制系统原理Fig.3 Principle of control system
此外,根据图2分析可知,该电机中5次谐波的幅值和相位分别是3.234.1V和161°,因此,再由式(5)可计算得到所需注入的谐波电流特性满足以下公式:
(13)
3.2 仿真结果
图4为基于MATLAB/Simulink仿真计算得到的注入谐波电流前、后的转矩波形对比。可以看到:在注入谐波之前,系统的转矩在5~7 N·m之间波动;而注入谐波之后,转矩在5.5~6.8 N·m之间波动。显然,注入谐波之后转矩脉动被大大抑制,这与前面理论分析相符。
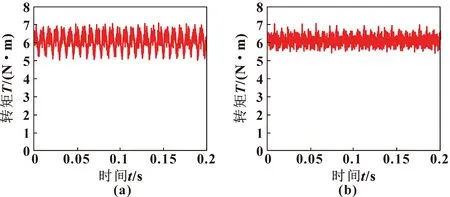
图4 注入谐波前(a)、注入谐波后(b)转矩波形对比Fig.4 Compare of torque waveforms before injecting harmonics (a)and after injecting harmonics(b)
图5对比了注入谐波前、后系统转速的波形。可以看到:与转矩波形类似,当采用谐波注入时,转速波形脉动也得到了明显改善。
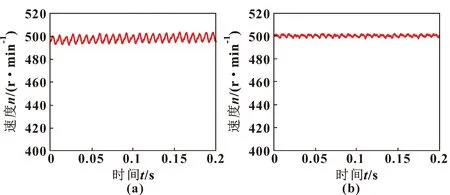
图5 注入谐波前(a)、注入谐波后(b)转速波形对比Fig.5 Compare of speed waveforms before injecting harmonics(a)and after injecting harmonics(b)
因此,总体而言,所提出的基于谐波注入的方法不仅可以改善系统的控制精度,同时也可以降低振动噪声。
4 谐波注入控制系统试验验证
试验是检验理论分析的重要方法[13-14]。为了进一步验证上述所分析得到的控制方法的正确性,对一台12槽10极三相表贴式永磁电机进行了相应的试验研究。试验的控制器采用dSPACE控制面板,它可以直接编译Simulink 环境下的仿真模型,从而形成dSPACE试验平台可以辨识的代码,最终建立起可在线调整各项参数的试验系统,实现电机性能和控制方法试验。试验平台如图6所示。

图6 试验平台Fig.6 Experimental platform
利用示波器,保存试验过程中的电流和转矩数据,如图7所示。可以看到:注入谐波之后的电流波形发生了一定的畸变,使得其幅值有一定的增加,但是转矩脉动确实也有一定程度的降低,这也与前面的分析相吻合。可见,所提出的方法有效。
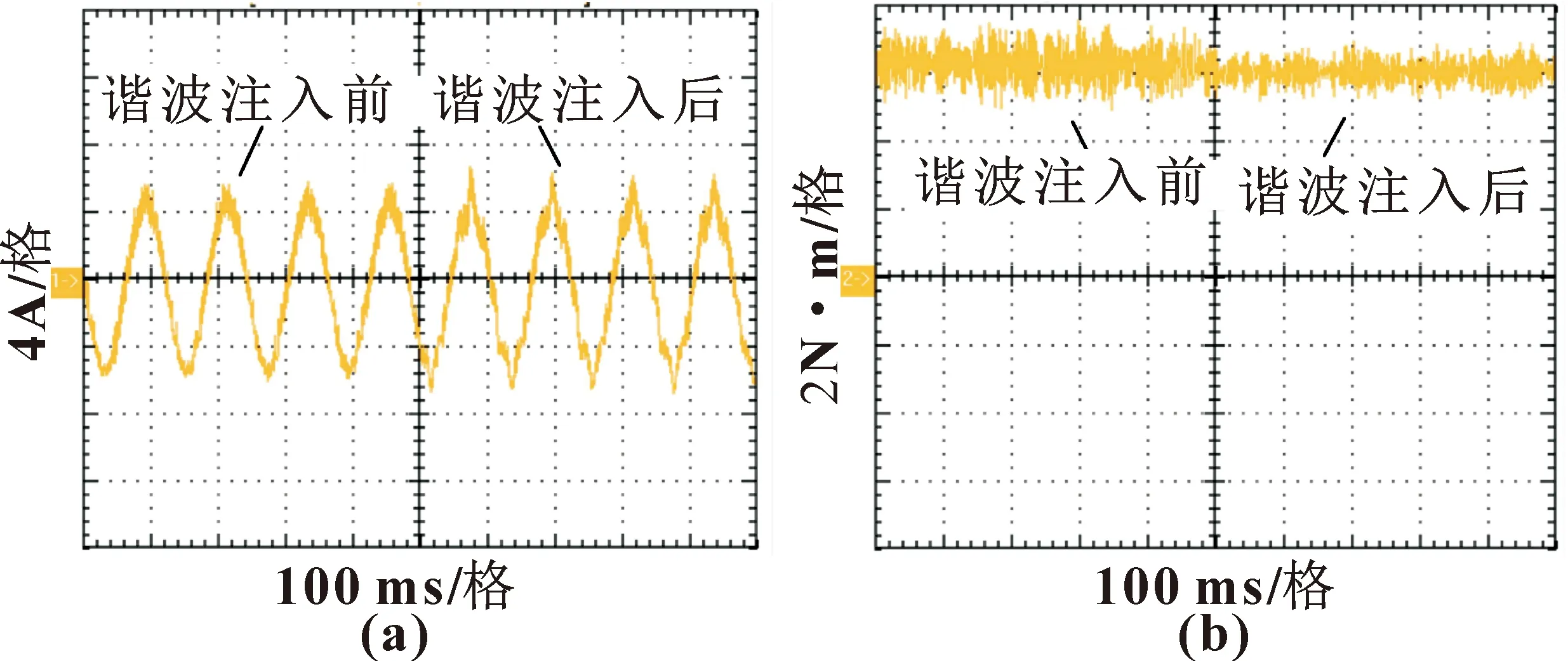
图7 电流(a)和转矩(b)试验测试波形Fig.7 Tested waveforms of current(a) and torque(b)
5 结束语
提出一种基于谐波注入的永磁电机模型预测电流控制方法。首先,建立了适用于任意相永磁电机反电动势谐波产生的脉动转矩通用解析模型;然后,基于此模型,从控制的角度出发,提出采用电流谐波注入以补偿反电动势谐波引起的转矩脉动控制策略,分析所需注入的电流谐波特性的一般表达式,并通过模型预测电流控制方法对电流进行控制。为验证所提出方法的有效性,以一台三相12槽10极表贴式永磁同步电机为例,通过MATLAB/Simulink设计了考虑反电动势谐波的电机仿真模型,搭建了基于谐波注入的电机控制系统。此外,为进一步验证所提出的方法正确性,也进行相应的试验验证。研究结果表明:谐波注入前、后电机的转矩脉动峰峰值从2 N·m降低到1.3 N·m。
