6-DOF主动波浪补偿液压平台的结构优化分析
2023-03-01王佳沈慧慧张国兴周昊宋世磊
王佳, 沈慧慧,张国兴,周昊,宋世磊
(1.江苏科技大学机械工程学院,江苏镇江 212003;2.上海船舶设备研究所,上海 200031)
0 前言
船舶受到海浪冲击,会产生横移、纵移、垂荡、横摇、纵摇和偏航6种类型的运动,使得海上船舶作业缺乏平稳性。因此,开发具有波浪补偿功能的船用波浪补偿液压平台,有利于提升海上作业工作效率和提高船舶设备工作的精确性[1-2]。船用波浪补偿液压平台因具备刚度大、结构稳定、承载能力强、精度高且运动惯性小等优点,被广泛应用到船用波浪补偿领域,称为船用波浪补偿液压平台。船用波浪补偿液压平台的作用是:使被稳定对象在受到海浪干扰时保持惯性坐标系下的相对稳定[3-4]。该平台主要由2个平台和若干条相同的液压缸组成,下平台固定于船舶甲板,上平台用于放置作业设备,所有液压缸的两端通过球形、万向或柔性接头连接到上、下平台[5-6]。
船用波浪补偿液压平台已在工程中得到重要应用。文献[7]以样机实验的形式,以三自由度平台为波浪模拟器,六自由度并联平台为主动波浪补偿器,证明了六自由度波浪补偿平台的波浪补偿功能。随着船用波浪补偿平台研究的日益深入,该类平台的结构优化设计逐渐成为研究的重点。优化平台的结构参数可以使得平台的性能提高,研制费用降低,平台的占地面积减小,使得平台结构更加紧凑合理等。文献[8]对波浪补偿平台的结构进行优化设计,证明了优化后的平台可补偿船舶在4级海况下的升沉、横摇和纵摇运动。文献[9-11]采用遗传算法,优化所有结构参数,得到全局运动性能最优的平台机构。文献[12]介绍了六自由度并联平台的结构优化设计与分析,从平台结构的优化设计入手,对该平台的结构参数进行了优化并获得更大范围的工作空间。文献[13-15]皆利用ADAMS软件建立运动模拟平台的参数化模型,分析了平台的运动学与动力学,对平台的结构进行优化。
通过比较上述的机构优化方法可知,利用虚拟样机技术的优化方法可有效避免复杂的理论计算与结构分析;并且能够在建立模型后,通过仿真获得机构运动学与动力学参数,不仅能够优化平台结构参数,缩短产品研发周期,提高工作效率,更为机构样机的研制提供更直观、更有效的数据支持与仿真分析。本文作者以UCU(上平台、支腿与下平台的连接副分别为虎克铰U、圆柱副C与虎克铰U的连接方式)型六自由度船用波浪补偿液压平台为研究对象,分析该平台的波浪补偿运动特性,建立其相应的参数化模型,并进行仿真研究及结构优化分析,最后利用SolidWorks软件建立该波浪补偿液压平台的三维模型并导入ADAMS软件中,对优化后的波浪补偿液压平台模型进行补偿能力的检验,证明该优化方法具备有效性与合理性。
1 波浪补偿液压平台机构的结构描述
UCU型六自由度船用波浪补偿液压平台的6条支腿由6根相同的液压缸组成,每根支腿液压缸的两端通过虎克铰连接到上、下平台,平台结构示意如图1所示。
如图1(a)所示,上平台为半径R1,下平台半径为R2,平台最低位置的初始高度为H。上平台的6个铰点依次为A1、A2、A3、A4、A5、A6,上平台铰接圆圆心点为O1;下平台的6个铰接点依次为B1、B2、B3、B4、B5、B6,下平台铰接圆圆心点为O2。图1(b)中,以上平台为例,L1为上平台上较近两铰接点之间的直线长度,该参数代表铰接点的分布规律,同理,L2为下平台上较近两铰接点之间的直线长度。综上可知,R1、R2、H、L1、L25项参数决定了波浪补偿液压平台的结构尺寸。给定该六自由度船用波浪补偿液压平台的波浪补偿技术指标如表1所示。
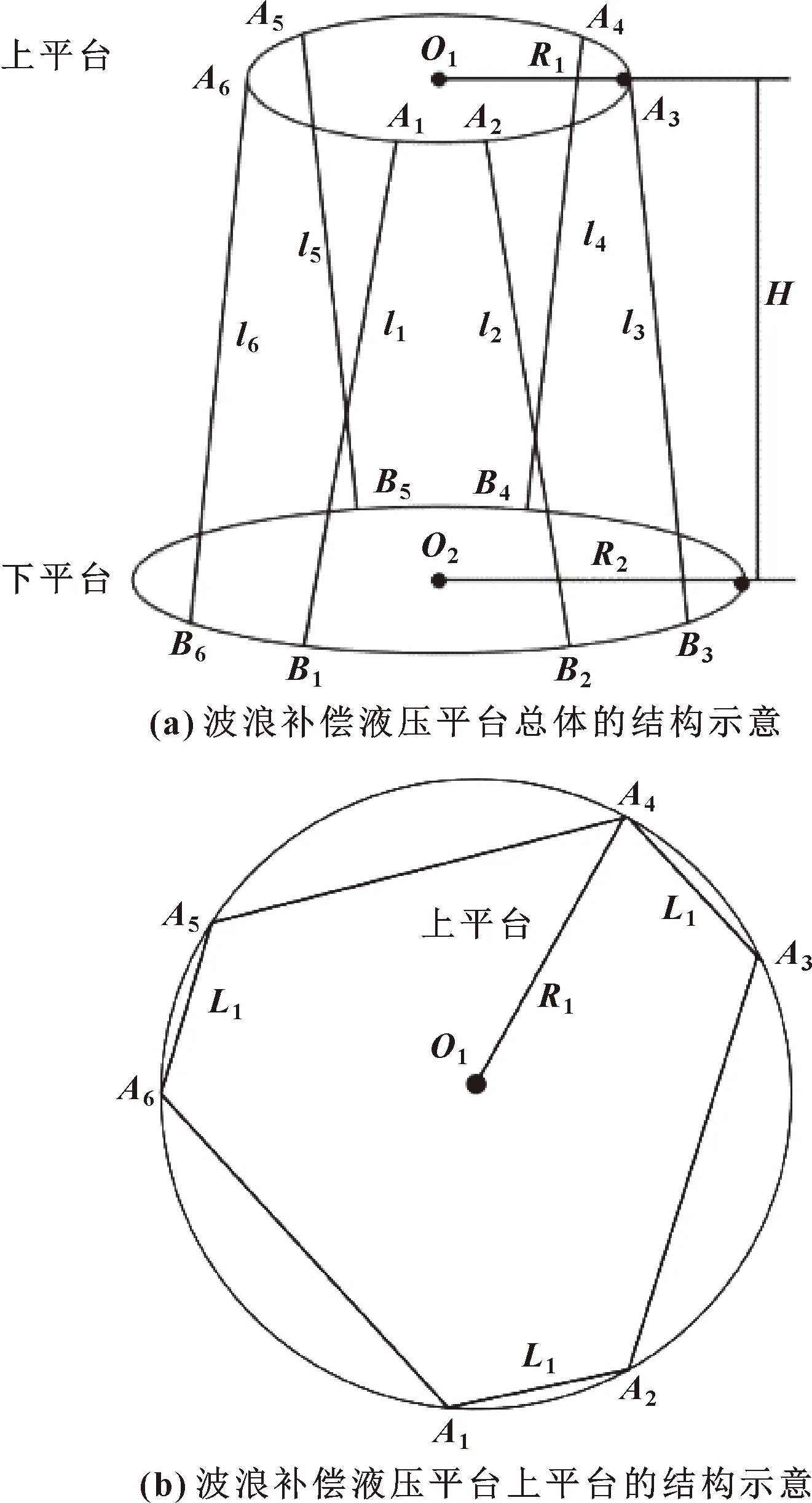
图1 波浪补偿液压平台的结构
表1为该波浪补偿液压平台后续的优化设计工作提出要求。以表1中的波浪补偿液压平台技术要求作为标准,建立该波浪补偿液压平台的参数化模型,在最终的波浪补偿能力检验阶段,表1可作为验证模型是否满足波浪补偿功能的标准,具体实现流程如图2所示。

表1 波浪补偿液压平台的技术指标

图2 波浪补偿液压平台优化设计流程
以该平台的技术指标为起始点开始设计,若最终建立的最优结构平台模型能够满足已提出的技术指标,则表示此次对平台的结构优化能够确保该平台具备合格的补偿功能。
2 波浪补偿液压平台参数化模型的建立
通过对波浪补偿液压平台结构尺寸的分析,结合上述提出的该平台波浪补偿技术指标,分3个步骤建立波浪补偿液压平台的参数化模型。
(1)确定设计变量。波浪补偿液压平台的结构尺寸主要由图1中描述的5项结构参数(R1、R2、H、L1、L2)决定,选取该5项结构参数作为参数化模型的设计变量,其标准值与取值范围皆根据已提出的平台所需的波浪补偿技术指标得出。在后续的优化过程中,利用ADAMS软件集成的优化算法对波浪补偿液压平台的参数化模型进行优化,会更进一步地在已设置的取值范围内寻求满足优化目标的最优解。上述5项结构参数设计变量的取值设置如表2所示。
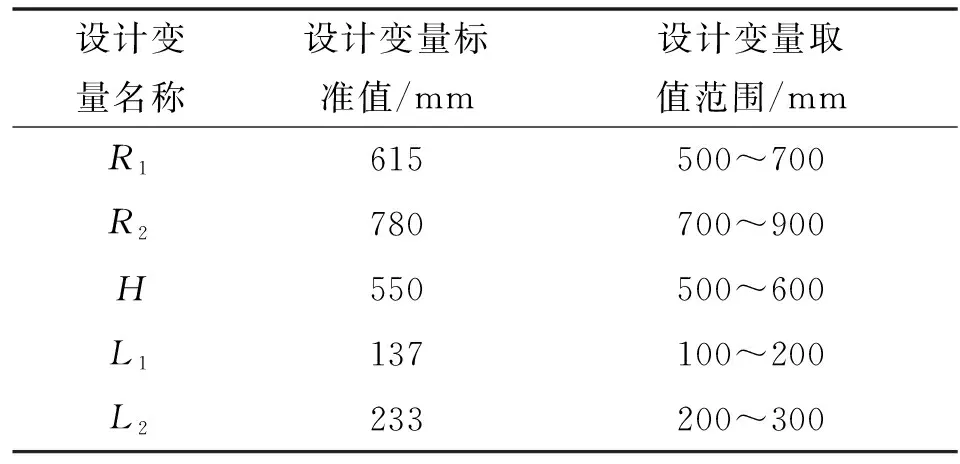
表2 平台的设计变量
(2)参数化关键点。平台的12个铰点的空间坐标决定了5项设计变量的大小,建立铰点A1、A2、A3、A4、A5、A6与B1、B2、B3、B4、B5、B6的参数化坐标,使其作为参数化建模的关键点,在ADAMS软件中,设置12个关键点的参数化坐标值,如图3所示。
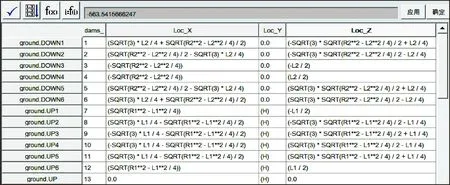
图3 波浪补偿液压平台关键点的坐标
图3中DOWNi(i=1,2,3,4,5,6)与UPi(i=1,2,3,4,5,6)分别代表下铰点与上铰点的坐标名称,UP为上平台圆心。文中共设计15个实体,其中上、下平台由2个大直径圆柱体表示,6根液压缸由长圆柱体表示,液压筒由一端面封闭的圆筒表示,机构上平台中心点加载一个正方体表示负载。根据已建立好的12个关键点与实体,添加约束,每个液压缸两端与两平台连接处皆用虎克铰进行约束,6根缸的相对运动为圆柱副运动。由于12个关键点的坐标值全部由设计变量表达,则建立实体、添加运动约束时进行的参数化将在此12个关键点的基础上设计,最终达到平台模型的参数化。建立好的参数化模型如图4所示。
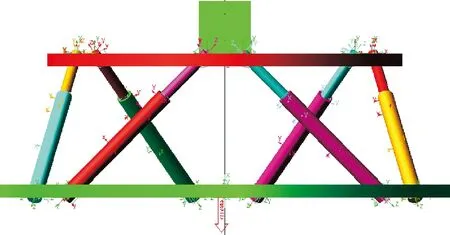
图4 波浪补偿液压平台的参数化模型
(3)设置优化条件。以步骤(2)获得的参数化模型作为基础,定义该模型的测量、约束方程,其中,需要定义的测量值有支腿液压缸的长度与液压缸的驱动力值。
由下述公式定义支腿液压缸长度的约束方程:
Lmin=Ldead+Lstroke
(1)
Lmax=Ldead+2×Lstroke
(2)
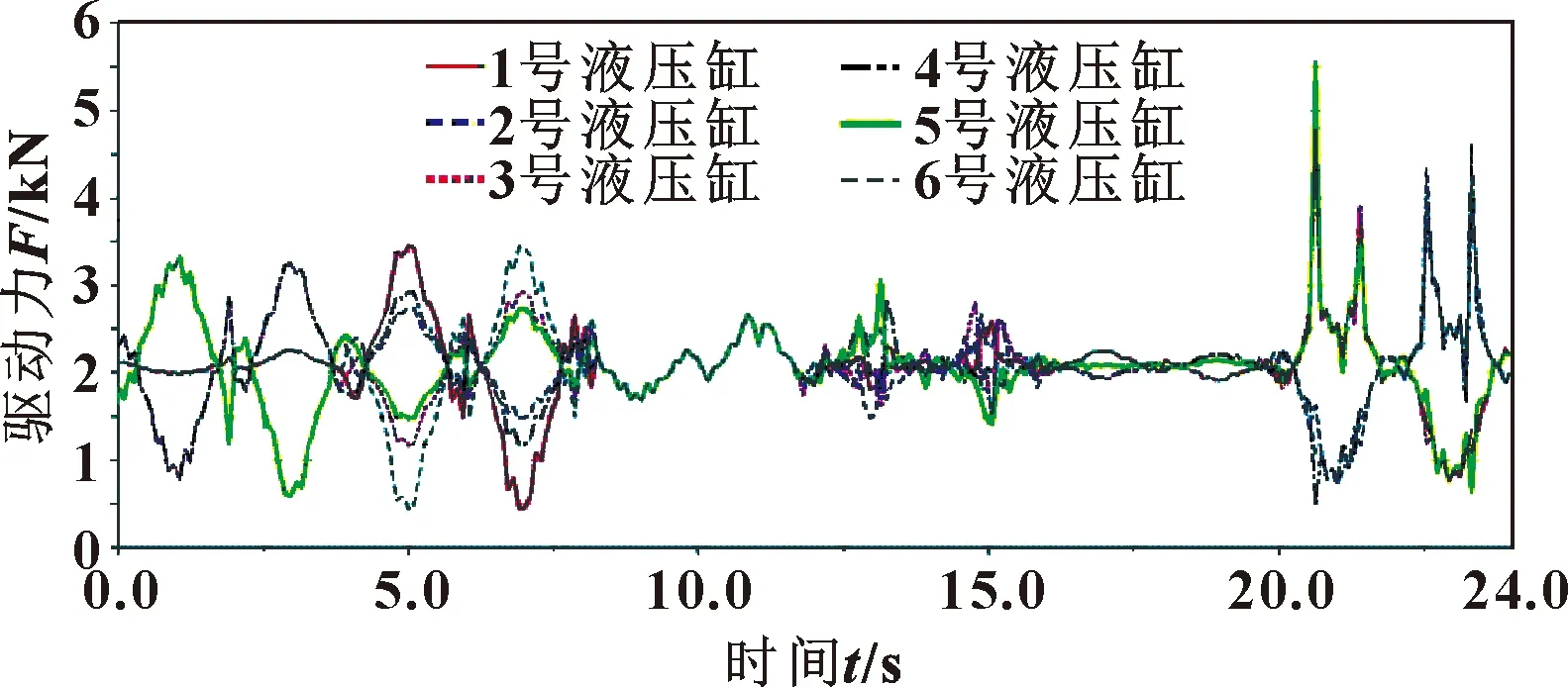
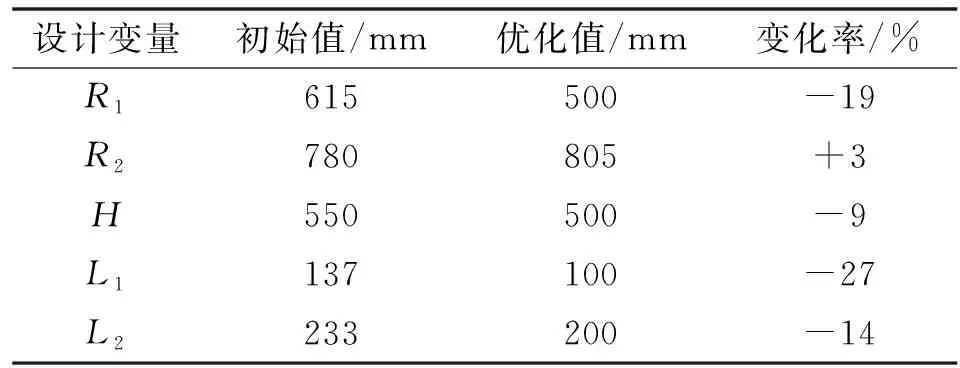
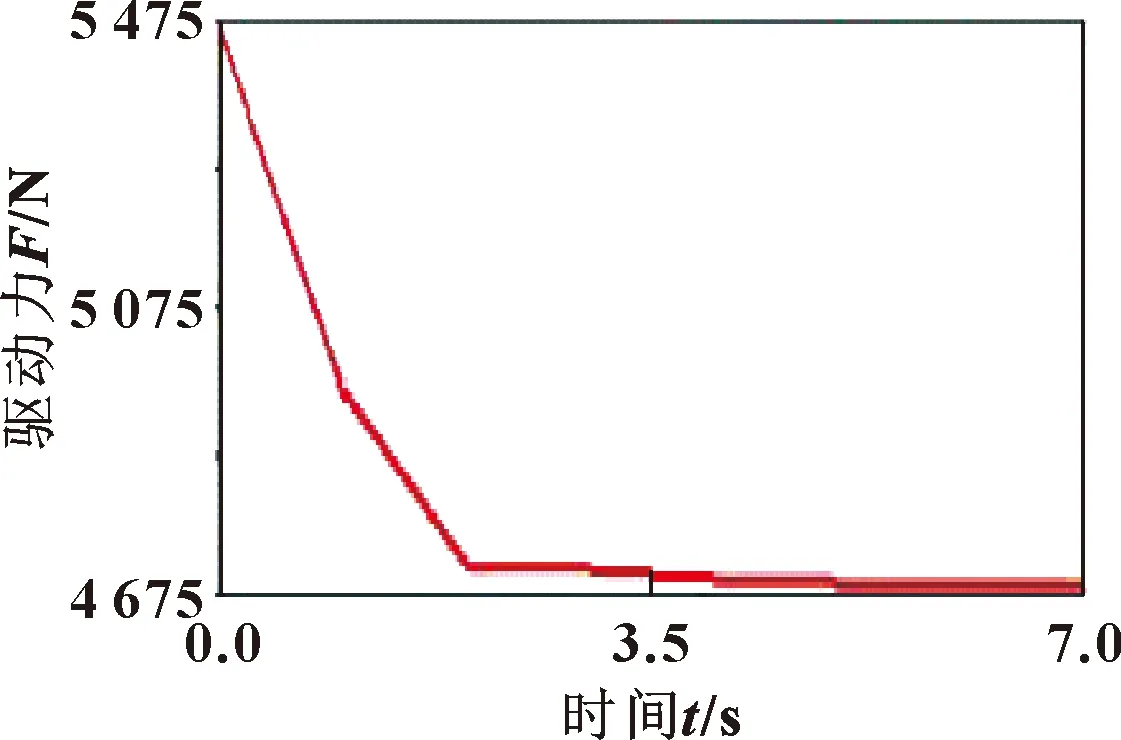
其中:Lmin与Lmax分别为支腿液压缸的最小长度值与最大长度值;Ldead与Lstroke分别为支腿液压缸的固定长度与行程长度。根据提出的技术指标,设此次Ldead长度为300 mm,Lstroke长度为400 mm,则可得Lmax长度为1 100 mm。以支腿液压缸的总长不超过1 100 mm作为约束方程的约束条件。其余约束函数表示为:L1 从经济效益与工作效率出发,波浪补偿液压平台应在满足规定波浪补偿指标的同时,能有更好的负载能力,即在一定的负载条件下,液压缸受力的最大值越小越好,故选取液压缸的最大驱动力为优化目标。由于六自由度船用波浪补偿液压平台的6根支腿是统一规格的液压缸,则提供最大驱动力的支腿液压缸决定了6根液压缸的规格,因此应先找到最大驱动力产生的支腿液压缸,以该支腿液压缸的最大驱动力为优化目标进行优化。首先,在上平台的ground.UP点处,利用STEP驱动函数添加广义驱动,在24 s时间段内依次完成6个自由度的运动,每4 s完成一个自由度运动的往返,每个自由度的运动极限值都达到技术指标的极限数值。遍历该24 s的运动,则可完成平台波浪补偿的技术指标,将该24 s的运动称为指标运动。该上平台驱动函数的设置如图5所示。 图5 波浪补偿液压平台运动函数 添加如图5所示的驱动函数后,对模型进行运动学仿真分析,获得6个液压缸质心与液压缸筒质心相对位移的曲线图后,将曲线采集的数据进行拟合,通过样条函数spline得到样条线型数据,删除原有加在上平台中心的驱动,再利用Akima Fitting Method(AKISPL)函数将样条曲线数据赋值到对应的6个液压缸的驱动函数上,使上平台完成6个自由度的指标运动。对此时的模型进行仿真分析,即可得到6根液压缸驱动力随时间变化的曲线,如图6所示。可知:6根液压缸的最大驱动力出现在5号液压缸上,其值为5 558 N,因此创建对Motion5的幅值力测量,作为优化目标。 图6 初始波浪补偿液压平台各液压缸的驱动力 以支腿液压缸的最大行程约束为例,优化工具中约束条件设置时,应满足的格式为:OPT_CONST_i-1 100<0(i=1,…,6),优化目标为5号液压缸的驱动力,研究其最大值,选择5个设计变量。优化模型的准备工作完成后,利用ADAMS软件Design Evaluation Tools中的OPTDES-SQP算法优化模型,得到优化后的结果,保留整数后总结见表3。 表3 平台模型优化结果 由表3可知:优化后的平台模型结构参数总体呈现下降的趋势,即平台的总体积减小、紧凑性提升。平台模型5号液压缸的驱动力变化如图7所示。 图7 5号液压缸最大驱动力变化 由图7可知:在此优化过程中,优化目标5号液压缸的最大驱动力由最初的5 558 N减少到4 697 N,液压缸的最大驱动力较之前优化了约15%,可见该优化设计有效地改善了液压缸的受力情况。 为保证优化后的平台模型能满足技术指标要求,对平台进行补偿功能的检验。使用表3中的优化值,在SolidWorks软件中建立起平台的三维模型,并保存为Parasolid(*.x_t)格式。将优化模型导入ADAMS软件中,进行工作环境的设置,再根据模型的运动功能添加运动副。工作环境设置完成后ADAMS环境下的优化模型如图8所示。 图8 ADAMS环境下的优化模型 图8为优化模型在ADAMS环境中的预处理,对上平台添加广义驱动,同理用STEP函数,进行上述的指标运动,使得上平台的行程满足指标要求。 在指标运动过程中,机构运动流畅且无卡顿现象,且得到6根支腿液压缸的行程随时间变化曲线,如图9所示。 图9 6根支腿液压缸的行程变化 由图9可知:在指标运动过程中,液压缸的行程最大值约为350 mm,相较于初始设计的液压缸行程(Lstroke=400 mm),液压缸的行程减小了13%。因此,可证明优化模型具备合格的补偿功能,由于行程越小的液压缸的价格越低,因此节省了平台制造的成本。综上所述,平台的优化模型能够满足指标工作的运动要求,并且能有效地降低平台在加工制造时的生产成本。 为确保优化后的模型各支腿液压缸驱动力都得到有效的优化,并且优化后驱动力的最大值仍然出现在5号支腿液压缸上,测量优化后的模型支腿液压缸驱动力如图10所示。 图10 优化后波浪补偿液压平台各液压缸的驱动力 从图10可以看出:优化后的波浪补偿液压平台各支腿液压缸的驱动力都有了明显的减小,其中最大的驱动力仍然出现在5号液压缸上,其值约为4 752 N,图10与图6皆呈现上下对称的状态,图6在驱动力约为2 000 N处上下对称,图10在驱动力约为1 750 N处上下对称,证明了此次液压缸驱动力优化的有效性与正确性。 文中提出一种在ADAMS软件提供的仿真环境中对UCU型六自由度船用波浪补偿液压平台的结构尺寸进行优化的方法,该方法采用虚拟样机技术建立平台的参数化模型,使得平台结构尺寸的优化过程更加简单快捷,提升该类液压平台的设计效率、缩短研发周期。以减小支腿液压缸的最大驱动力为优化目标,对平台的5项结构尺寸进行优化分析,优化结果表明:平台在相同的负载指标条件下,液压缸最大驱动力较初始值减小了约15%,平台在具备合格补偿能力的条件下,支腿液压缸行程较优化前减小了约13%。此次优化分析不仅有效地提高了平台负载能力,缩小了平台的体积,实现了平台研制轻量化的目标,更为后续的船用波浪补偿液压平台样机设计及研究提供了有价值的参考。3 波浪补偿液压平台结构尺寸的优化
3.1 模型优化目标的选取
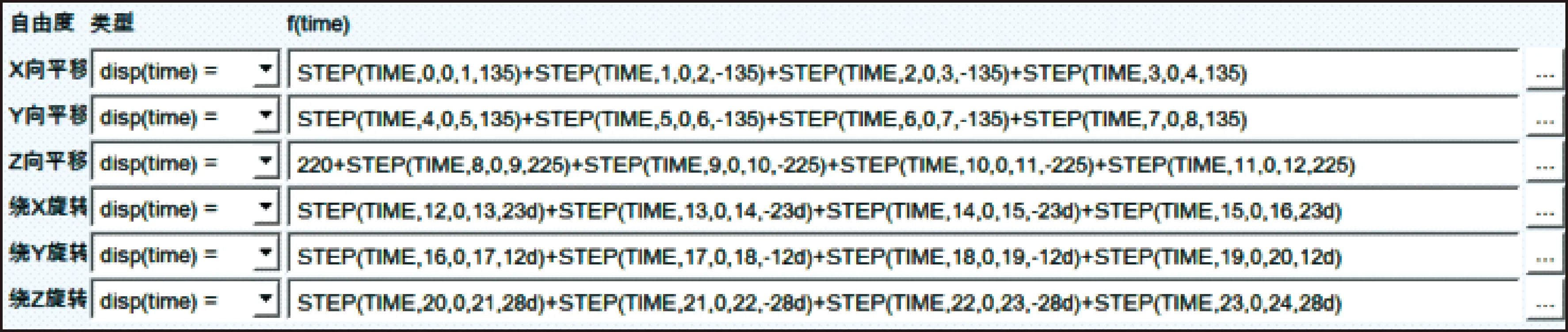
3.2 模型的优化结果与分析
4 优化后的模型分析验证
4.1 优化后模型的建立

4.2 优化后模型的验证
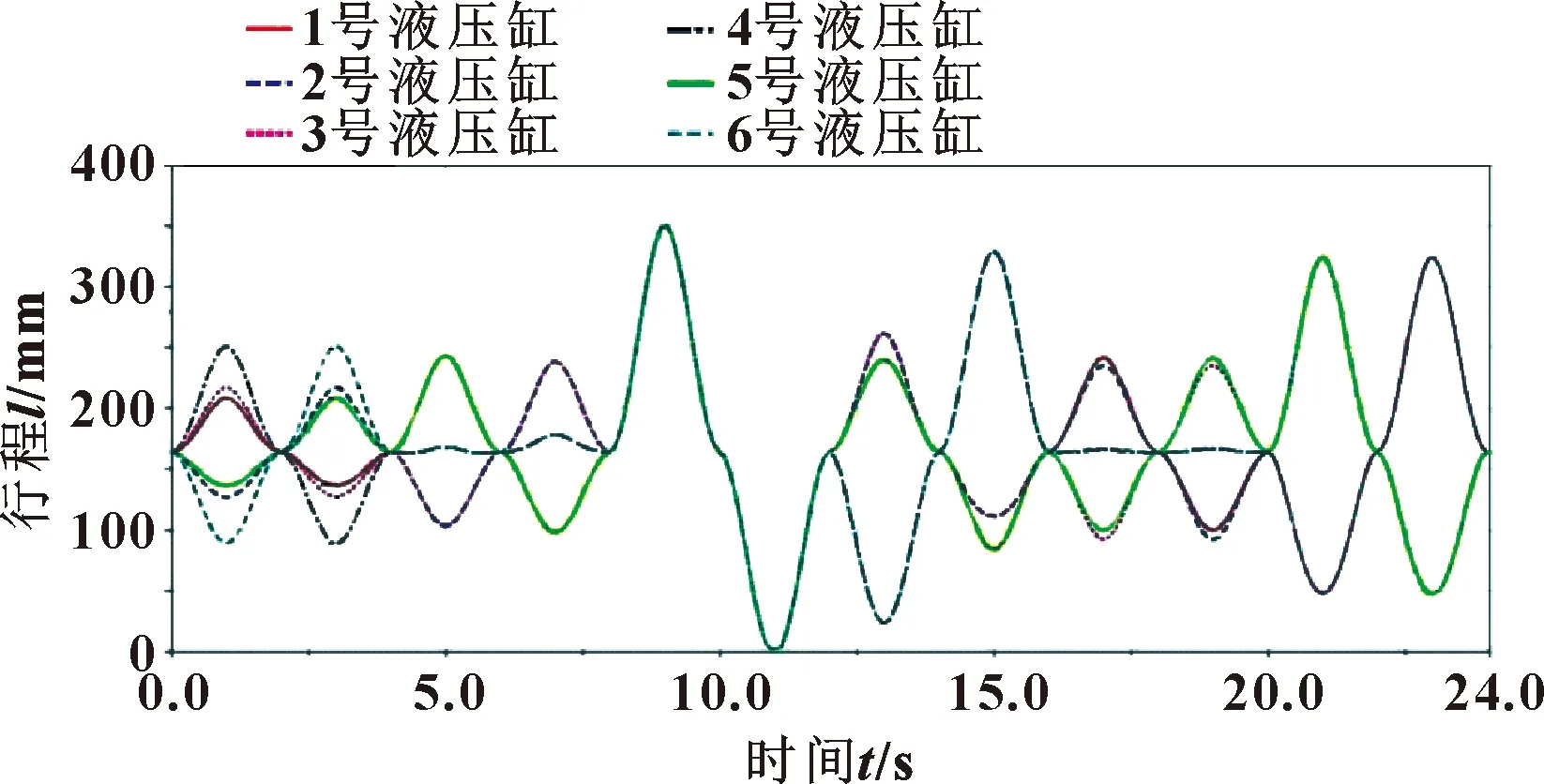
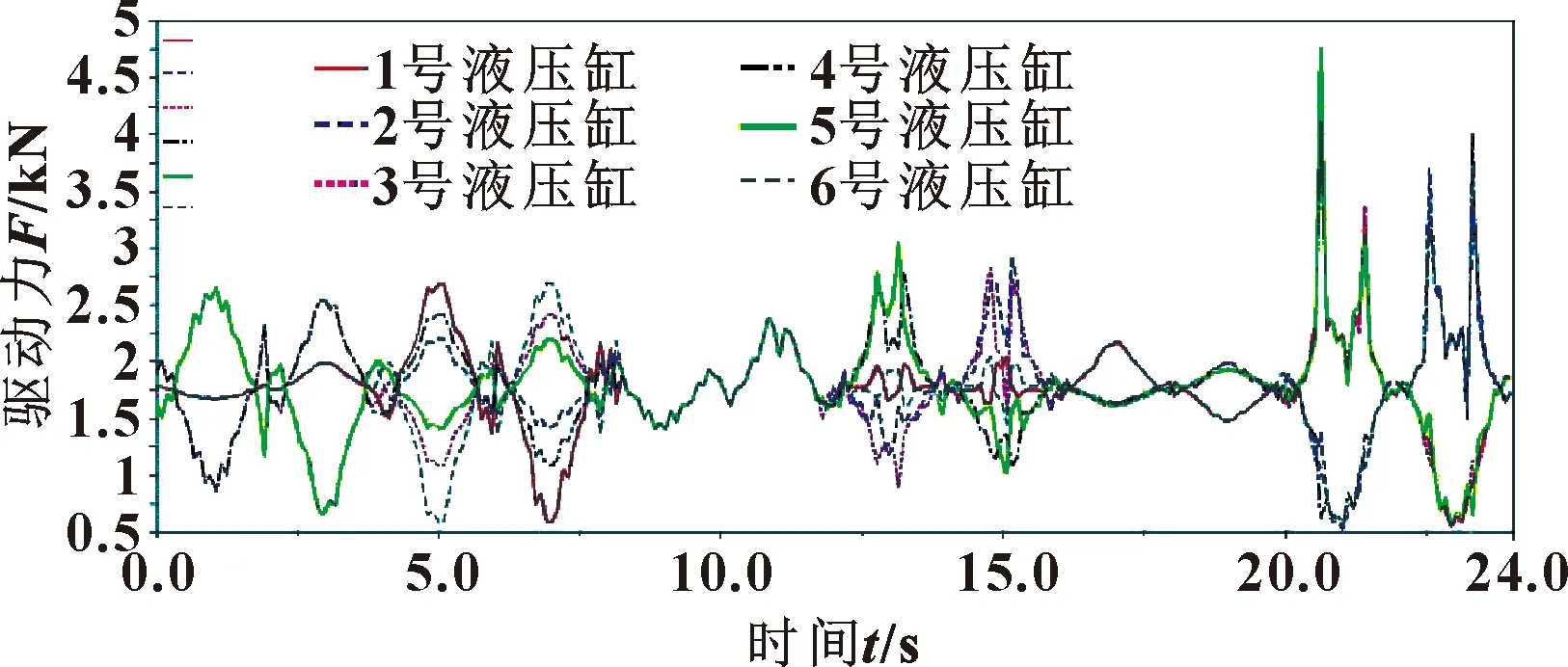
5 结论
