基于樽海鞘群优化网络模型的计量装置状态识别方法

郑克刚，袁安荣，雷 乾，张天旭，吴世强，冯小兵

（国网重庆市电力公司铜梁供电分公司，重庆 402560）

0 引 言

近些年，随着互联网和信息化的迅速发展，电力行业也逐渐推进智能化管理［1－2］，各电力公司和供电企业不断提升自身的客户服务精益化管理水平。电能计量装置作为关键性的电力企业和用户结算的仪表工具，其运行状态的正常与否会关系到计量结果的准确性和可靠性，并继而影响到后续相关电力业务的开展。 在传统的电能计量装置的检测工作中，主要是由人工巡检完成，人工成本高且效率低；而随着用电信息采集系统建设，当前系统内已积累了海量计量装置监测数据，且计量装置异常样本也达到了一定的体量，故可开展远程线上异常识别［3］，对计量装置状态进行识别。 从而可有效解决人工巡检的不及时性和不准确性，节约时间和人工成本。

当前，部分研究机构及专家已开展该方面的研究工作，如文献［4］采用支持向量机构建数据和任务并行化的故障诊断模型，实现对电能计量装置运行异常特征、故障状态的在线实时监测。 文献［5］基于电能表、电压互感器和电流互感器的历史故障、运行环境等数据，组建不同的评价指标，将模糊分析法与层次分析法相结合、对计量装置的运行状态进行评估。 文献［6］使用营销系统数据和计量生产调度平台数据等参数，对电能表进行不同影响因素下的基础测试，并以此建立评估模型对电能表进行状态评估。 虽然上述方法均在一定程度上实现了计量装置的远程运行状态监测［7］，但由于未结合时序数据加以分析，导致监测效果并不理想。 针对上述问题，本文提出了基于樽海鞘群优化调参的计量装置状态识别模型。

1 整体过程描述

为了及时准确识别在电能计量装置的运行状态，本文构建了基于樽海鞘群优化网络模型的计量装置状态识别方法。 模型整体流程如图1 所示。

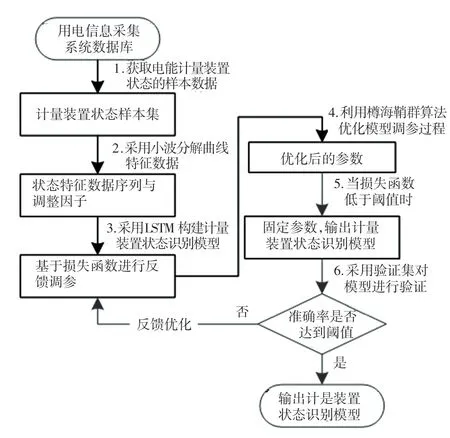
图1 系统结构框图Fig. 1 Structure diagram of the system

本文首先利用小波分解对样本集的数据进行分解，然后对分解出的高低频数据特征作为计量装置状态的关联时序特征，分析其与运行年限、生产厂家、状态数据、运行环境等影响因素间的相关性，构建相应的运行年限、生产厂家和运行环境调整因子。将小波分解后的状态关联时序特征与调整因子作为长短期记忆网络输入，而后利用长短期记忆网络（LSTM）进行计量装置状态分类，输出分类结果，基于输出结果与真实结果构建交叉熵损失函数，并根据损失函数进行反馈调参，再采用樽海鞘群算法优化模型的调参过程，以提升调参速度与识别精准性。

2 基于樽海鞘群优化调参的计量装置状态识别模型

本文针对电能计量装置包含的电能表、电压互感器、电流互感器进行远程运行状态监测，异常状态主要针对远程数据可表征的电能表计量异常、电能表损坏、互感器损坏［8］。 通过用电信息采集系统的数据库获取涉及电能计量装置状态的样本数据，加以汇总整理后进行数据预处理，构建计量装置状态样本集，然后按照70%、20%和10%比例分为训练样本集、验证样本集和测试样本集。 电能计量装置状态数据的主要特征包括电压、电流、用电量、相位、开关量、运行时间、运行环境数据等。

2.1 基于小波分解的特征提取与分析

针对上述样本集数据的电压、电流、用电量等曲线特征，采用小波分解［9］算法中的wavedec函数将特征数据进行D层小波分解，获取小波分解系数矩阵C和矩阵内系数的个数L：

其中，A为输入的特征数据；M为分解层数；C为小波分解系数；sym4 表示小波变换方式；L为小波分解系数的个数，即矩阵内系数的个数。 如经过3层小波分解后，共包含4 个高低频特征，分别是：1 个低频近似特征值和3 个高频细节特征值。

根据分解出的数据特征结合计量装置样本状态、运行年限、生产厂家、状态数据、运行环境等与计量装置样本状态的相关性，构建相应的运行年限、生产厂家和运行环境调整因子K。

2.2 构建计量装置状态识别模型

本次电能计量装置的运行状态分为正常状态、注意状态和异常状态。 采用LSTM 算法构建计量装置状态识别模型，将小波分解后的状态特征数据序列与调整因子K作为长短期记忆网络的输入，根据LSTM 算法中门控装置的3 个控制门（输入门、遗忘门和输出门）来实现对输入样本集数据的识别和计量装置状态的判别。 3 个控制门控、记忆信息及输出判别的数据处理过程可阐释分述如下。

（1）更新忘记门输出为：

更新输入门2 部分输出为：

（2）记忆信息状态为：

（3）更新输出门输出为：

更新当前样本的计量装置状态判别预测输出为：

其中，Wf、Wi、Wa、Wo与Uf、Ui、Ua、Uo分别为输入的隐藏层和输入样本的权重参数；t －1 为上一神经单元；t为当前LSTM 神经单元；bf、bi、ba、bo为偏移量参数。

将Softmax函数作为LSTM 神经单元网络训练的最后一层，在经过门控装置的训练后会输出样本状态类别预测概率值，再利用多分类交叉熵损失函数计算出样本数据的期望输出预测概率值和实际输出概率的误差、即损失，Softmax函数定义如下：

其中，yi为样本计量装置状态判别的预测输出值，C为分类的类别个数。

基于输出结果与真实结果构建交叉熵损失函数，交叉熵损失函数定义如下：

其中，P为样本的实际状态类别；T为模型的判别输出；C为分类的类别个数，这里，T ＝［softmax（y1），softmax（y2），…，softmax（yi ＝n）］。

根据损失函数构建梯度反馈函数进行调参，采用樽海鞘群算法［10］提升LSTM 网络的调参速度与精准性。 樽海鞘群算法（salp swarm algorithm，SSA）对一个D 维空间进行寻优搜索，樽海鞘种群的个体数为N，樽海鞘种群的位置向量可由矩阵X表示：

食物的位置是所有樽海鞘个体的目标位置，樽海鞘个体领导者的位置根据食物的位置进行更新，其位置更新公式为：

其中，l为当前迭代次数，L为最大迭代次数。c1在搜索前期值较大，便于全局寻优，迅速确定全局最优点；在搜索后期值变小，起到局部开发的作用。c1起到平衡全局探索和局部开发的作用，是樽海鞘群算法中最重要的参数。

樽海鞘种群追随者的位置移动规律，在求解过程中的时间就是迭代过程，设每次迭代过程中的时间t ＝1，每次迭代的初速度v0＝0，表示为：

式（12）和式（14）描述了整个樽海鞘群体内部的移动机制。

利用樽海鞘群算法寻找计量装置状态识别模型的最优参数的流程如下：

（1）初始化参数。 根据搜索空间每一维的上界与下界，初始化一个规模为D ×N的樽海鞘群，D表示参数个数，d∈［1，2，…，D］，在每一维空间中分别生成包含N个个体的随机种群X，根据樽海鞘群算法，计算每个解xj（j ＝1，2，…，N） 的初始适应度，适应度为模型识别类别判别概率的提升，即参数θd为xi时，相比于当前θd值，其Softmax（yxj i） 概率值提升，则说明其适应度提升，二进制向量转化为：

因此，只有对应于1 的xj被取出来表示适应度满足条件，作为备选领导者的参数。

（2）选定目标位置。 由于实际调参过程中不知道目标参数的位置，因此，将樽海鞘群按照适应度值进行排序，排在首位的适应度最优的樽海鞘的位置设为当前目标位置。

（3）选定领导者与追随者。 选定目标位置后，群体中剩余N －1 个樽海鞘，按照樽海鞘群体的排序，将二进制向量为1 的樽海鞘视为领导者，其余樽海鞘视为追随者。

（4）位置更新。 先根据式（12）更新领导者的位置，再根据式（14）更新追随者的位置。

（6）重复步骤（3）～（5），直至达到一定迭代次数或适应度值达到终止门限、满足终止条件后，输出当前的解的位置作为目标的估计位置，即返回全局最优解。

损失函数低于设定阈值后，固定参数，输出计量装置状态识别模型，采用验证集对该模型进行验证，验证准确率与召回率达到设定阈值后，输出模型，否则继续进行反馈优化。

3 实验结果与分析

实验部分选取测试样本集的数据对该模型的有效性进行测试。 在本文所提模型中输入测试集中的样本数据，记录其准确率和召回率，同时，将本文算法与SVM、逻辑回归、贝叶斯和BP 神经网络四种算法进行识别性能的对比。 在测试中，主要采用准确率、精确率和召回率三个指标来衡量，各指标定义具体如下。

（1） 准确率ACC（accuracy），计算公式为：

（2）精确率P（precision）。 计算公式为：

（3）召回率R（recall）。 计算公式为：

其中，TP、TN、FP、FN表示的含义见表1。

表1 参数含义Tab. 1 Parameters meaning

本文所提方法与其他4 种算法的性能对比结果见表2。

表2 算法性能对比Tab. 2 Performance comparison of algorithm%

此实验分别对比了各种算法识别的准确率和召回率，可以看到，其他4 类算法虽也表现出不错的识别性能，但是本文所提方法的准确率和召回率具有明显的优势。 实验结果表明，本文采用长短期记忆网络构建计量装置状态识别模型，有效提升了状态识别的准确率和召回率。

消融实验分别对3 组测试数据进行测试，控制变量是采用樽海鞘群算法和不采用樽海鞘群算法，精确度实验结果和时间对比实验结果分别如图2 和图3 所示。 其中，时间对比实验是基于当前训练完成后的模型，以测试样本集作为二次训练样本集，将其识别准确度作为目标函数进行二次调参，对比传统反馈调参方式，本文所提的樽海鞘群调参可在更短的时间内完成参数寻优过程，且由精确度对比数据可看出，樽海鞘群调参可基于全局探索跳出一定的局部最优，从而有效提高了模型的识别性能。 从实验结果图可以看到，3 组数据都表现出了同一种趋势，即采用樽海鞘群算法的模型具有更高的精确度和更快的调参速度，上述均表明本文所提计量装置状态识别模型具有良好的性能。

图2 精度对比图Fig. 2 Accuracy comparison chart

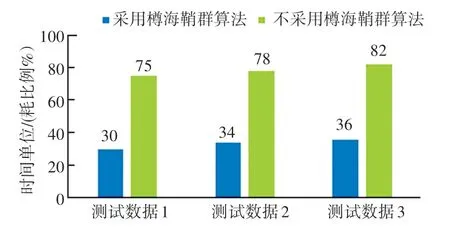
图3 参数调整时间对比图Fig. 3 Recognition time comparison chart

4 结束语

文中提出了一种基于樽海鞘群优化网络调参的计量装置状态识别模型，首先采用小波分解算法进行曲线特征分解，并构建多因素的影响因子，随后采用LSTM 算法构建状态识别模型，基于时序记忆的异常状态识别提高了计量装置状态的识别准确率，并利用樽海鞘群算法提高了模型的调参速度，从而提升了整个异常识别方法的识别效率和准确率，模型具有极高的可用性和可靠性。 本文计量装置状态识别模型的提出，有效增强了供电公司客户服务部门的数据分析能力，提升了客户服务精益化管理水平。