指向深度学习的高三复习教学策略
——以2022 年新高考全国I 卷数学试卷第17 题为例
2023-02-28宋建辉
宋建辉
(福州格致中学,福建 福州 350001)
一、问题的提出
素养导向的学习如何开展?深度学习是一条路径.素养导向的高考命题,[1]不仅考查学生对数学知识的学习和掌握,而且更注重对学生学科素养和学习能力的考查,因此要立足深度学习开展课堂教学.我国对“深度学习”这一概念的界定始于黎加厚教授,[2]“深度学习”重视对知识的深度加工与理解,引导学生针对学科的核心问题开展深度探究,通过问题串的学习任务激发学生的学习兴趣,达成掌握学科核心知识、把握知识的内在联系、提升解决问题的能力.
目前高三复习教学存在的问题是忽视发展学生的思维能力,集中于模式化、套路化解题为主,不在意学生是否理解,从而造成“机械学习”的盛行,只是重视“题海训练”,机械模仿刷题,这对学生未来的数学学习将产生严重的消极影响.基于“深度学习”概念的界定和高三复习现状,本文立足“选取符合学生学情的、经典的数学试题”进行教学设计,通过一道试题的解法探究、变式探究、联想类比等教学环节,梳理数列知识的内部逻辑联系,渗透数学基本思想与方法,促进深度学习的动机发生和深度学习的习惯养成,从而提升深度学习的能力和思维品质.本文以2022 年全国新高考I 卷数学试卷第17 题的深度探究开设一节研究课,以探索高三复习教学中激发学生深度学习的教学方式.
二、教学设计思路
数列作为高中数学重要研究对象之一,为解决实际问题提供了切实好用的数学模型,也是对运算、抽象和推理等思维能力进行综合训练的素材,因此,高中生对数列的学习不应只是计算和解题的循环,如何将深度学习理论运用到数列的学习中是一个值得研究的问题.由此,笔者设计了如下的教学思路,以此展开一个“深度学习”的实践探索过程.

三、背景分析
(一)考情分析.本题是2022 年新高考全国I 卷中一道数列试题,放在解答题中的第一题位置,命题者明显是想“送分”,但有相当同学拿不到这10 分.全省均分在4 分左右,从考后对部分学生访谈,发现不同水平的考生的解题障碍在于得到关系式“(n-1)an=(n+1)an-1”如何求通项公式没有明确的解题思路,暴露了部分考生的逻辑推理素养的缺失,反映了“深度学习”下探究能力的欠缺.
(二)学情分析.本节课的授课对象是笔者任教的一个班级,该班是一个物理方向的普通班级,学生的学习热情较高,思维较为活跃,解决问题的思路较多.
四、教学过程
(一)典例剖析,促进学生深度思考
哈尔莫斯说“问题是数学的心脏”.在课堂教学中,一个好的数学问题、一个经典的数学问题可以激发学生学习的兴趣,启动学生积极的思维活动,引发深度学习的动机,进而完成对数学学习的各自特征与相互关系的整体把握.由此,笔者设计了以下试题.
试题呈现:2021 年高考数学新高考卷I 第17 题.

【设计意图】在复习课教学设计中,问题的设计应该尽可能以学生的最近发展区为基础,贴近学生的已有认知,显然,高考试题是最好选择,高考试题不仅能激发学生的数学思维,而且能唤起学生从问题解决到深度学习的欲望.
师:由已知条件入手,根据等差数列的概念及通项公式容易得到Sn与an的递推关系,第(1)问求an的通项公式,自然想法是利用an=Sn-Sn-1(n≥2)关系消Sn求an:

在得到①式后,由于是求an的通项公式,自然是消Sn得到an的递推关系.
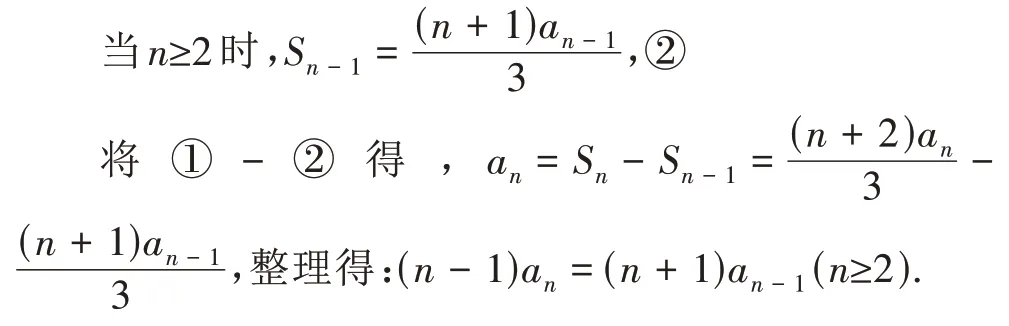
由(n-1)an=(n+1)an-1求通项公式是本题学生的“卡”点之处,因此课堂上教师给予学生充分时间,在教师引导下,经过学生长时间、热烈的讨论,学生得到如下解法.


教师:从以上4 种不同解法中,同学们将已有知识、方法进行优化整合,使深度学习自然发生.方法1中“累乘法、类加法”源自教材中等差数列、等比数列通项公式的推导方法,可谓源于教材高于教材;方法2与方法3 的“构造法”充分体现了化归与转化这一重要数学思想;方法4 的数学归纳法作为研究数列的基本方法,通过观察、归纳、猜想、证明等全过程展示,体现了这一思维的灵活性.
【设计意图】通过高考题把等差数列、等比数列、数列递推关系、an与Sn的关系等知识、方法联结起来,在问题的探究活动中立足基础知识、基本方法,让学生体会知识、方法间的内在联系,从而融会贯通,提高数学解题能力.
(二)变式探究,促进学生的深度迁移
问题引领是深度学习的起点,鼓励学生大胆地进行类比联想,提出新的问题,从而切实体现教师的主体地位,只有这样学生才能积极地参与教学活动,进行深度学习.
教师:上述问题以等差数列为载体考查了数列通项公式的求法,你们可以在此题背景下编拟新问题吗?
学生5:改为求数列{ }an的前n项和Sn.这样求Sn的方法就有两种:一是可由上述方法求出an后代入Sn=间接求得;二是直接求,即对上述的解法进行迁移运用,先消an,累乘求Sn,或先消an,构造等差数列求Sn.
【设计意图】将问题转化为求前n项和Sn,通过问题的变式,整合优化学生已有的知识结构、思维习惯和思维能力,灵活迁移,让学生的数学思维走向深入,实现深度学习.
(三)类比联想,促进学生的深度学习
深度学习是理解性学习,教师要对问题进行深层次加工,引导学生通过深切的体验和深入的思考,达成对问题的理解,经历“知其然、知其所以然、何以知其所以然、何以由然”的过程,让学生的思维从低阶走向高阶,从而促进学生深度学习的能力.鉴于此,笔者设计了如下问题.

教师:该题中的k=3 时即为高考题.从特殊到一般是一种非常重要的数学思想和思维方法,在问题的解决中要灵活应用,本题就留给同学们课后完成.
【设计意图】通过类比、拓展,根据学生的认知水平设计由浅入深、由表及里的学习过程,让学生的数学学习和思维不断深入,使学习成为一种“再发现再创造”的深度学习过程.
五、教学启示
本文通过2022 年全国新高考I 卷数学试卷第17题来发现学生存在的问题,通过挖掘学生思维障碍,把问题细化,通过问题变式,设置环环相扣的问题来搭建思维的桥梁,并展开一系列旨在问题解决所需的知识与技能的探究活动,[3]以此构成一个“深度学习”的探究学习过程,初步形成如下深度学习的教学方式:
(一)创设丰富问题情境,引导学生深度参与
深度学习强调迁移与应用,要求学生在深度理解的基础上做到举一反三,将知识迁移到新情境中解决新问题,而实现迁移的关键是学生能够对情境进行深入分析,把握情境的要素.这就需要教师根据知识内容的特点和学生的思维发展水平选择合适的情境,引导学生积极参与,锻炼对各种具体情境的分析能力,从而促进深度学习的发生.
(二)明确学生“最近发展区”,推动学生深入思考
教师应根据学生的“最近发展区”设置带有合理难度的问题或任务作为驱动,通过逐步深入的问题串让学生在探索中发现数学知识的真谛,同时在学生的探究过程中根据学生的思维特征有针对性地进行个别指导,从而促进深度学习的达成.
(三)注重知识的整合建构,促进学生深度探究
深度学习实质上是结构性与非结构性知识意义的建构过程,也是复杂的信息加工过程,须对己激活的先期知识和新知识进行有效和精细的深度加工,因此教学中需关注知识的整体性,促进学生的加工与建构.新课标为遵循知识内部的联系性,放弃之前以模块呈现知识点的方式,构建了四条主线,教师在进行教学设计时需遵循知识主线,摒弃单个知识点的课时教学方式,帮助学生建立完整的知识体系.
