筑坝粗粒料单线法湿化变形模型比较
2023-02-28孙向军潘家军周跃峰左永振
孙向军,潘家军,周跃峰,左永振
(长江科学院 水利部岩土力学与工程重点实验室,武汉 430010)
1 研究背景
粗粒料湿化变形指在一定应力状态下浸水,由于颗粒之间被水润滑及颗粒矿物浸水软化等原因,造成土颗粒破碎、重新排列、结构收缩而发生变形的现象[1]。目前,大多数学者通过单线法三轴湿化试验测量湿化轴向应变(简称“轴变”)与体积应变(简称“体变”),在试验数据基础上直接提出湿化变形数学模型。
湿化变形经验公式的数学形式主要有线型、幂函数型、指数型、双曲线型4类。
赵振梁等[2]认为各向等压条件下,湿化轴变、湿化体变与围压呈线性关系;程展林等[3]用线性方程拟合了湿化体变与湿化应力水平之间的关系,线性方程中拟合参数与围压呈线性关系;陈剑[4]认为湿化轴应变与湿化应力水平之间亦呈线性关系,线性方程中拟合参数与围压也呈线性关系;李广信[5]认为各向等压湿化体变与围压呈幂函数关系。
指数函数主要用于拟合湿化轴变与湿化应力水平之间的关系,指数方程的拟合参数与围压间的关系,程展林等[3]认为与围压无关,迟世春等[6]采用幂函数形式拟合,牛昂[7]采用指数函数及线性函数拟合。
双曲线型函数在湿化轴向应变与湿化剪切应变中最为常见,沈珠江等[8]最早建立了湿化剪切应变与湿化应力水平之间的双曲线关系,傅华等[9]对其进行了验证;张少宏等[10]提出湿化轴向应力与湿化轴向应变之间满足双曲线关系。
周雄雄[11]在湿化体积应变与湿化轴向应变的比值、广义剪应力和球应力三者满足扭面关系基础上,对迟世春模型做了进一步推广。除此外,针对高围压高应力水平条件下湿化变形的不规律变化,部分学者提出了其他湿化变形模型,如杨小龙[12]建立了引入平均主应力和临界应力水平的分段函数湿化体变经验公式,魏松等[13]基于最大湿化应力水平物理量,建立了复合式湿化应变模型;左永振等[14]从砾石土心墙料试验结果角度分析了该现象产生原因。
国外学者对粗粒料湿化变形的研究,侧重于探究影响湿化变形的因素,鲜有经验公式提出,值得一提的是Oldecop等[15-16]早年基于非饱和土理论,将基质吸力引入粗粒料湿化变形研究中;后来又考虑时间效应,将时间因素亦引入粗粒料湿化变形研究之中。
上述经验模型,大多仅由一种粗粒料个数较少的试验数据拟合得到,模型的适用性无从得知,目前更无采用统一定量标准来比较已有经验公式拟合精度的相关研究。对此,本文就搜集的文献试验数据进行验证研究,以便为合理选取经验公式提供参考,并为寻求更合理的湿化模型提供指导依据。
2 湿化物理量及模型精度
2.1 应力量
目前大部分湿化变形试验均采用σ2=σ3的常规三轴湿化试验,将其代入得平均应力(主应力第一不变量)p及偏应力(应力偏张量第二不变量)q,即
(1)
2.2 应力水平量
(2)
2.3 湿化变形量
连续力学定义剪应变γ及体应变εv为
(3)
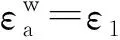
(4)
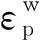
2.4 模型精度量
由于涉及多个数据,故本文优先选用相对误差的标准差δ作为模型拟合优劣的标准,δ越小,表明拟合效果越好。δ计算公式为
(5)
除本节列出及后文特别指出含义的符号外,后文出现的其余符号均为模型拟合参数。
3 湿化变形模型及验证
3.1 等压湿化应变模型
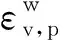
直线型[2]:
(6)
双曲线型[17]:
(7)
幂函数型[5]:
(8)
本文就3种模型对等压湿化体变进行验证研究,由于目前大部分为数不多的等压三轴湿化试验仅在3种围压下进行,对3个数据拟合明显不合理。故本文仅对文献[9]2种不同密度的堆石混合料、文献[13]花岗岩料,在4种围压条件下的等压湿化试验数据进行拟合验证,其相对误差的标准差δ如表1所示。
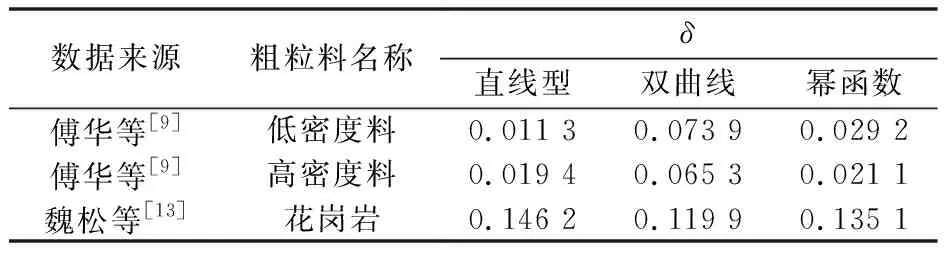
表1 等压湿化体积应变模型δ结果Table 1 Standard deviation δ of relative error of wetting volumetric deformation models under constant pressure
由表1可知,3组试验数据拟合结果表明,采用幂函数型曲线拟合,拟合效果均不是最差的,故建议在上述3种等压湿化体积应变模型中选择时,优先选用幂函数型。
3.2 湿化轴向应变模型
在三轴湿化试验中,湿化轴向应变的测试结果
较为准确,因此其公式数量较多,主要如下。
指数型Ⅰ(程展林等[3],m≈0,c≈0);
(9)
指数型Ⅱ(迟世春等[6]):
(10)
指数型Ⅲ(牛昂[7]):
(11)
双曲线型Ⅰ:
(12)
双曲线型Ⅱ(周雄雄[11]):
(13)
双线型(陈剑[4]):
(14)

表2 湿化轴向应变模型δ结果Table 2 Standard deviation δ of relative error of wetting axial strain models
3.3 湿化体积应变模型
沈珠江提出湿化体积应变为常量后,李国英等[17]、李全明等[18]提出的早期湿化体变模型仅含围压,与应力水平无关,故本文不加以验证。本文仅对方绪顺[19]提出的幂线型湿化体变计算公式、程展林等[3]提出的经典双线性公式、彭凯等[20]提出的六参数湿化体变公式进行验证,3类模型公式如下。
幂线型(方绪顺[19]):
(15)
双线型(程展林等[3]):
(16)
六参数型(彭凯等[20]):
(17)

表3 湿化体积应变模型δ结果Table 3 Standard deviation δ of relative error of wetting volumetric deformation models
由表3可知,在上述3种模型中选择时,建议优先选用程展林提出的形式简单、参数易于确定的双直线型经验模型,其拟合精度较幂线型及六参数型更好。
3.4 湿化剪切应变模型
目前文献可见的湿化剪切应变模型均认为湿化剪切应变与应力水平呈双曲线关系,以文献[14]砾石土心墙料数据为例,绘制湿化剪切应变γw与应力水平S/(1-S)的关系如图1所示。
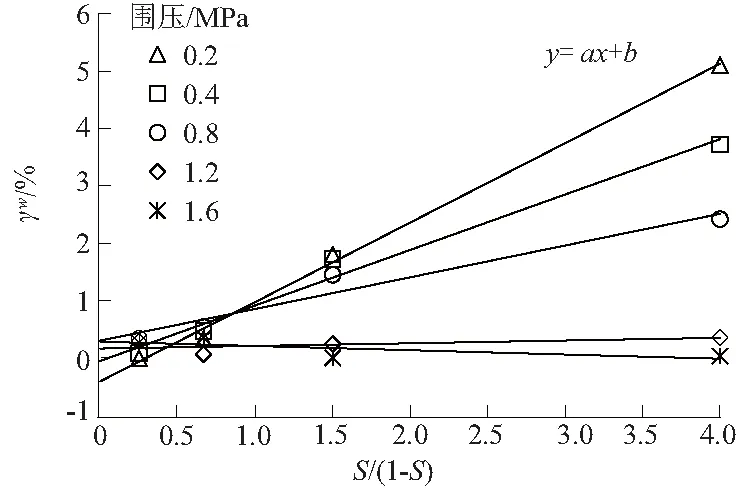
图1 湿化剪应变与应力水平的关系Fig.1 Relation between wetting shear strain and stress level
由图1可知,γw与S/(1-S)呈良好的线性关系,其两个参数(一次项系数a与常数项b)与围压σ3/pa的关系曲线如图2所示(图2公式中将σ3/pa简记为Z),一次项系数a用指数函数拟合,相关系数为0.96;常数项b用对数函数拟合,相关系数为0.85,拟合效果均较好。

图2 系数与围压Fig.2 Relation between coefficient and confining pressure
综上,本文建立的湿化剪应变经验公式如式(18)所示。
(18)
由于湿化剪切应变试验数据是通过公式(4)计算得到的,因此会出现多个湿化剪切应变接近于0的情况,此时再采用公式(5)计算相对误差的标准差δ作为评价模型拟合优劣的标准,将会过分凸显湿化剪切应变接近于0的数据,使拟合精度评判结果失真。故本文再引进绝对误差的标准差U,将其作为衡量模型拟合精度的指标,U越小,表明拟合效果越好。U计算公式为
(19)
本文就该模型对搜集到的数据进行拟合,其拟合精度U及拟合参数f、g、h、k如表4所示。
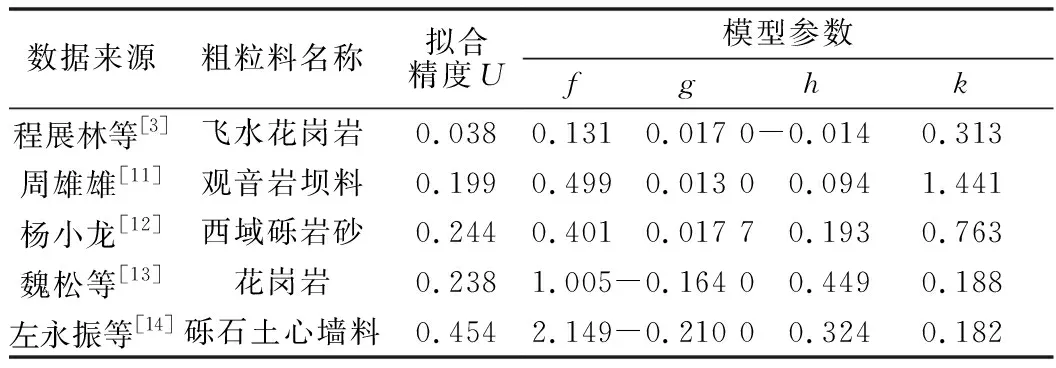
表4 湿化剪应变模型拟合结果Table 4 Fitting results of wetting shear strain model
由表4可知,经验公式(18)拟合效果较好,参数g在0值左右摆动,这表明湿化剪切变形受围压影响较小,常数项b与围压呈增长率最为缓慢的对数型关系,进一步表明了该结论。故在简明使用情况下,可考虑直接采用与围压无关的经验公式(20)进行拟合。
(20)
计算表明,式中参数A一般在0.15~0.60范围波动,B一般在-0.05~0.40范围波动。利用该式,在未做试验之前,即可粗略估计湿化剪应变。该式具有显著统计意义,不排除个别试验数据存在较大误差。
4 湿化变形模型改进
早在2006年,魏松[21]在博士论文中提出最大湿化应力水平与相对湿化应力水平的概念,成功解释了“在较高湿化应力水平下湿化轴变低围压的大于高围压的”现象,并建立了式(21)所示的湿化体变模型,此后该概念被加以搁置。
(21)

(22)
本文以程展林等[3]和左永振等[22]详尽的飞水花岗岩料单双线法试验数据为例,分析3种不同应力水平与各种湿化变形之间的相关联程度,并建立改进的拟合经验公式。
4.1 3种湿化应力水平
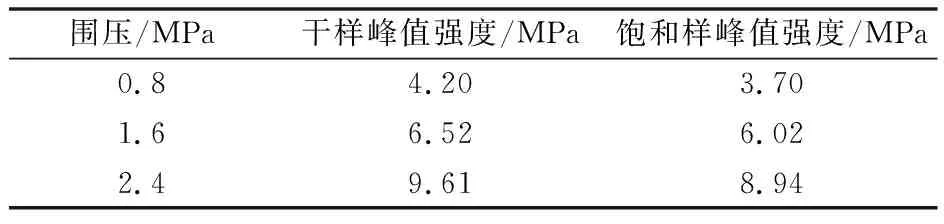
表5 偏应力峰值Table 5 Peak deviatoric stresses
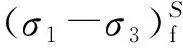
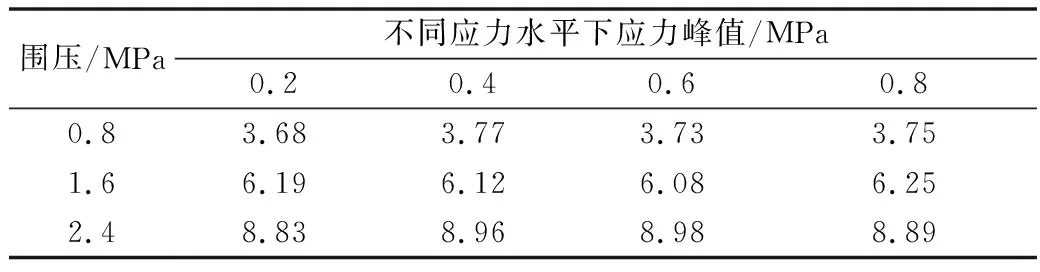
表6 湿化偏应力峰值Table 6 Peak wetting deviatoric stresses
实际的湿化应力水平和控制湿化应力水平存在差异,故表6中所列应力水平S仅为控制应力水平,其对应的实际应力水平量S实见表7。
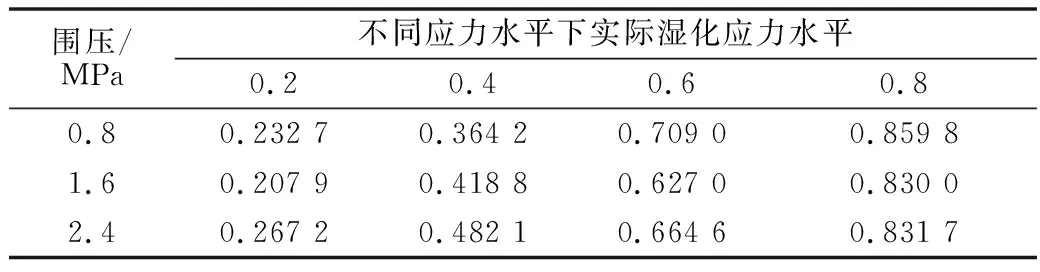
表7 实际湿化应力水平Table 7 Actual wetting stress levels
关于表5—表7数据更为详细的介绍,见文献[22]。
由表5—表7数值,依据式(2)、式(22)可得相对应力水平及改进相对应力水平如表8所示。
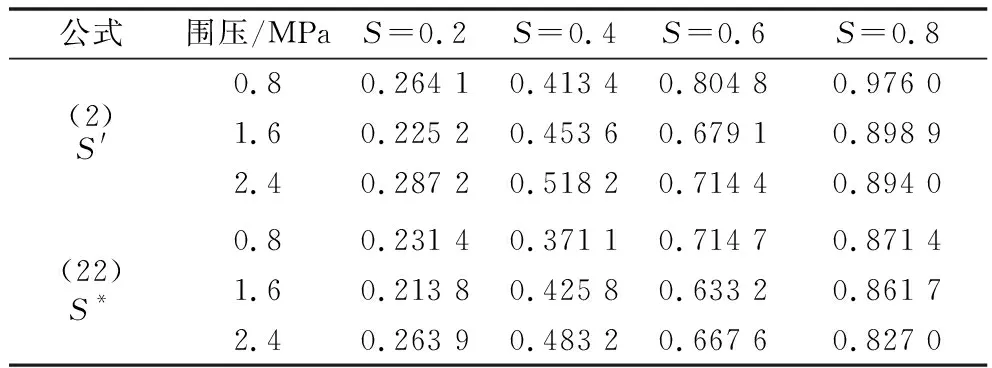
表8 相对应力水平Table 8 Relative stress levels
由表8可知,式(2)所得相对湿化应力水平S′对实际应力水平S实放大幅度较大,公式(22)所得改进相对湿化应力水平S*对实际应力水平S实改动幅度较小,且对有些值放大化,有些值缩小化。
4.2 应力水平与湿化变形的统计相关性分析
记X=应力水平,Y=湿化变形,由统计学知识可分析二者之间的相关联程度。
目前,衡量两个变量之间的线性相关程度,应用最广泛的当属Pearson相关系数r,其定义如式(23)所示,r取值为-1~1,越接近1,表示两个量正线性相关,越接近-1,表示负线性相关;接近或者等于0,表示两个量之间的线性关系很弱或不是线性关系。
(23)
在Pearson相关系数r的定义中用秩次(U,V)代替(X,Y)时,即可得Kendall相关系数ρ,其主要用来衡量两个量之间的单调相关性,当一个变量随另一个变量严格单调递增时,ρ=1;反之,ρ=-1。因ui、vi均为1至n之间的整数,故可简化ρ计算公式为式(24)。
(24)
2007年,基于相似性测度的Minkowshi距离,Skzely等[23]提出一种新的相关性分析方法:距离相关分析。已有研究表明,当变量间非线性关联时,利用其能够很好地探测到变量间的非线性或者非单调性的关系,但理论及具体计算较为复杂。本文基于两个数据间的绝对值距离,推导最为简单的经验距离相关系数的计算公式。
首先计算两个变量各自观测值两两之间的绝对值距离akl、bkl,k、l=1,2,…,n。
(25)
接着,在n×n的绝对值距离矩阵(akl)n×n、(bkl)n×n的基础上,计算对应的n×n经验双中心矩阵(Akl)n×n、(Bkl)n×n,即
(26)
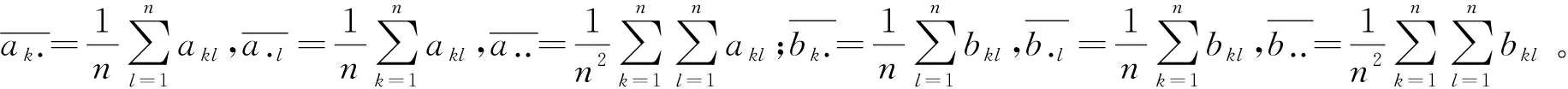
最后定义经验距离相关系数dCor(式(27)),dCor为0,表明两个变量独立;dCor越接近 1,表明两个变量相关性越好。
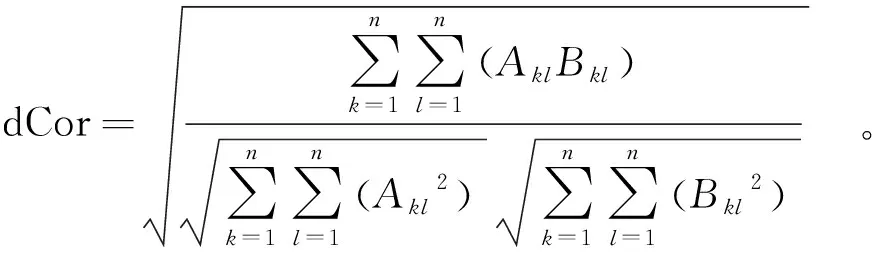
(27)
飞水花岗岩试验数据的上述3类相关性指标计算结果如表9所示。

表9 相关分析结果Table 9 Correlation analysis results
由Pearson相关系数r结果知,3种湿化应力水平中,与εaw、εvw线性相关程度最强的是实际湿化应力水平,最差的为S′,与γw的线性相关性,S*弱于其他2个湿化应力水平。
由Kendall相关系数ρ结果知,湿化变形随应力水平呈递增关系,S′及S*较S实而言,与湿化变形的单调相关性变弱,且S′及S*与湿化变形的单调相关性程度一样,这表明从单调相关性角度看,二者优劣程度一致。
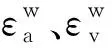
综上,在相关分析结果指导下,建立基于改进湿化应力水平S*的湿化变形模型具有可行性。
4.3 基于改进湿化应力水平的湿化变形经验公式
由3.2研究结论知,湿化轴向应变与应力水平用指数曲线拟合较好,故本文分别以S′及S*为自变量,采用指数函数拟合试验数据,拟合结果如图3所示。
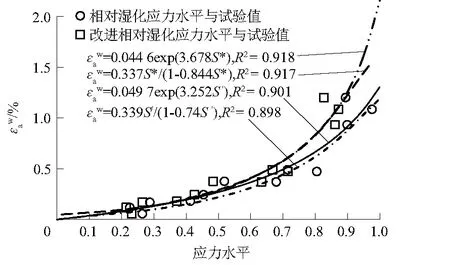
图3 湿化轴向应变与湿化应力水平Fig.3 Fitted wetting axial strain versus wetting stress level
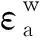
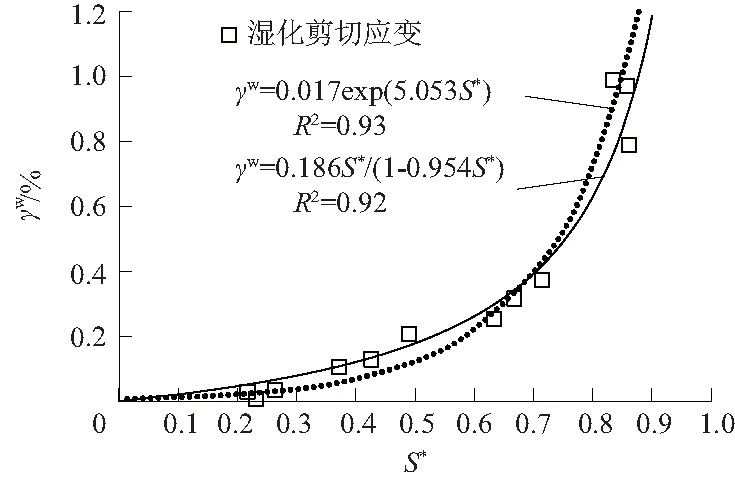
图4 湿化剪切应变与改进相对湿化应力水平Fig.4 Fitted wetting shear strain versus modified relative wetting stress level
由图4可知,指数型或双曲线型拟合结果均较好,指数型优点在于与εaw公式形式一致,双曲线型优点在于与3.4节研究结论一致。
由式(4)变形得εvw=3(εaw-γw),故可利用此对湿化剪切变形公式采用指数型还是双曲线型作出取舍,即验证式(28)与式(29)的拟合精度,拟合结果如表10所示。
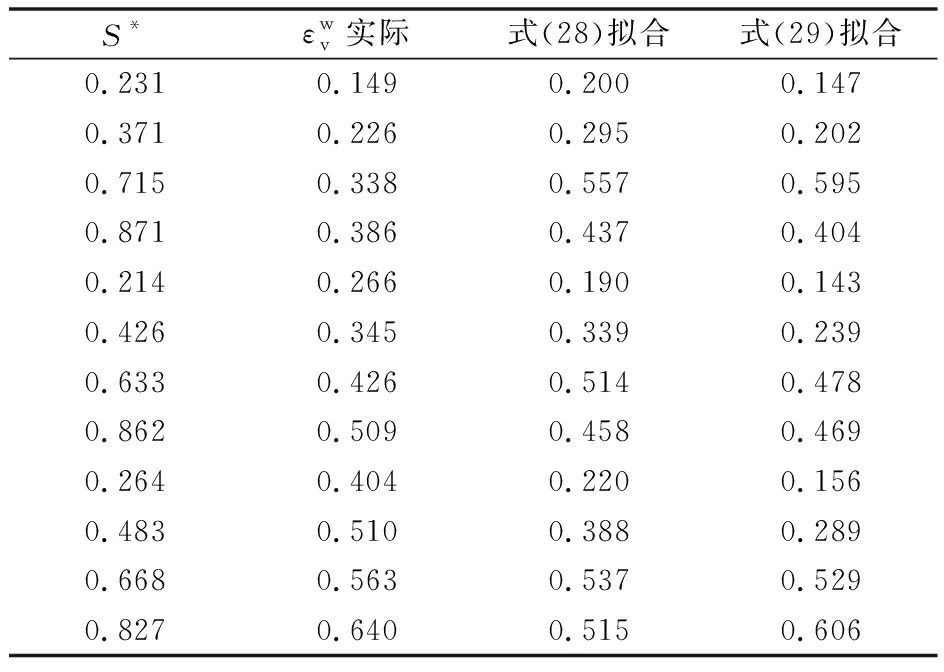
表10 湿化体积应变拟合结果Table 10 Fitting results of wetting volumetric strain
(28)
(29)
式中A、B、C、D为湿化轴向、剪切应变拟合公式参数。
由表10可知,只有高围压低湿化应力水平条件下,式(28)的拟合精度才优于式(29),故大部分情况优先选用式(29)。
综上,本文建立的基于改进相对湿化应力水平的湿化应变模型如式(30)所示,该式尤为适用于低围压情况。下一步可继续研究模型参数A、B、C、D与围压的关系,简便起见使用,可假定其与围压无关。
(30)
5 结 语
本文对搜集的文献试验数据进行了大量拟合验证研究,得出如下结论:
(1)等压湿化体积应变与围压用幂函数型关系拟合效果较好。
(2)湿化轴向应变与应力水平用指数曲线拟合精度较好,其模型系数与围压用线性关系拟合优于其他形式;湿化体积应变采用双线型模型,形式简单且拟合精度较幂线型及六参数型好。
(3)湿化剪切应变与应力水平呈良好的双曲线关系,模型参数与围压关系不大,故给出了在未做试验之前,即可粗略估计湿化剪切应变的经验公式(20)。
本文在计算3类衡量湿化应力水平的物理量与3种湿化变形物理量,两两之间的相关程度基础之上,提出了基于改进相对湿化应力水平的湿化应变经验公式(30)。
上述研究成果对提高筑坝粗粒料的湿化变形预测精度有一定的理论价值和实际意义。应该注意到,本文仅基于室内试验数据,验证了湿化应变的变化规律,下一步还需将湿化应变模型代入实际的土石坝工程中,计算湿化变形,与现场监测量进行对比,以验证模型的优劣。
