基于GRU算法的盾构掘进参数预测——以成都地铁19号线为例

肖浩汉，陈祖煜，徐国鑫，蒋宗全，苏 岩，曹瑞琅，刘诗洋

(1.中国水利水电科学研究院 岩土工程研究所，北京 100048； 2.陕西省引汉济渭工程建设有限公司，西安 710010； 3.中电建铁路建设投资集团有限公司，北京 100038； 4.同济大学 软件学院，上海 200092)

1 研究背景

随着基础建设逐步推进，隧道掘进机(TBM/盾构机)广泛应用于地铁、铁路、公路、市政、水电隧道等工程[1-2]。目前盾构掘进参数仍受驾驶者行为驱动，存在因经验不足而导致工程风险的可能性。林存刚等[3]回顾了杭州轨道工程在粉砂地层操作不当导致盾构刀盘被砂土裹牢事故，盾构机受困无法转动，最终被迫停工；王超等[4]分析了过快的掘进速度导致扭矩过大，从而刀盘磨损过快。在隧道掘进过程中，由于地质条件、环境因素、机械参数等众多因素影响，准确预测掘进参数仍十分困难[5-6]。随着盾构机采集数据的丰富，人工智能算法的发展，为预测复杂地质条件下盾构机的掘进参数提供了一种新思路。

盾构机掘进过程中，上位机从不同的传感器实时存储了数以亿计的数据。利用掘进数据，掘进参数预测模型可分为单目标预测和多目标预测。单目标预测方面，Lin等[5]提出了掘进速度的人工智能预测模型，结果表明所建立的人工智能模型的预测性能比经验模型的预测性能优异。闫长斌等[7]通过偏最小二乘回归确定了影响掘进速度的关键输入参数，构建了掘进速度的深度学习模型。更多的单参数预测模型可参考文献[8]—文献[11]。多目标预测方面，Sun等[12]根据地质参数和盾构机硬件参数构建了掘进速度、刀盘扭矩(T)和刀盘推力(F)的随机森林预测模型。周小雄等[13]基于盾构机上升段的掘进参数，建立了隧道掘进机双向长短期记忆模型，成功预测了稳定段的T和F。此外，李超等[14]建立的BP神经网络模型、侯少康等[15]提出的IPSO-BP混合模型、李建斌等[16]建立的极限学习机模型也均用于盾构机多目标掘进参数的预测。

盾构掘进参数的预测本质是一个多元时间序列回归问题，而人工智能算法中的循环神经网络对时序数据处理尤为擅长[17-18]。Gao等[19]使用了3种常用的循环神经网络，包括传统循环神经网络(Recurrent Neural Network，RNN)、长短期记忆(Long Short-term Memory，LSTM)和门控循环单元(Gated Recurrent Unit，GRU)，建立了盾构掘进参数的实时预测模型。Zhang等[20]基于LSTM模型提出了盾构掘进参数和沉降曲线的综合预测模型。此外，循环神经网络也广泛应用于地表沉降预测[21]、隧道涌水量预测[22]、岩性预测[23]、姿态轨迹预测[24]等领域。

目前人工智能算法在隧道盾构机领域已取得了一些成果，但对于盾构掘进参数的预测均较少讨论原始数据的异常特征和处理方法，且由于地质条件的特殊性和掘进设备的多样性，已有智能模型难以迁移。因此，基于成都轨道交通19号线二期工程土压平衡(Earth Pressure Balance，EPB)盾构机采集的掘进数据，开发了一种海量盾构掘进数据预处理的标准算法，建立了包含巴特沃斯滤波器(Butterworth filter)和GRU算法的多目标盾构掘进参数实时预测模型。通过回溯过去一段时间的盾构掘进参数预测下一阶段的T和F，研究成果可为成都地区或类似工程的EPB掘进提供指导。

2 数据来源及预处理

2.1 数据来源

2.1.1 工程简介

数据收集于成都轨道交通19号线二期工程，线路全长43.186 km，均为地下线，共设地下车站12座，平均站间距为3.58 km。目前隧道仍在建设中，研究数据来自新码头街站至红莲村南站区间(新红区间)左线98+732至99+865里程段，隧道开挖直径8.64 m，总长度1.13 km，共602环。

2.1.2 地质条件

新红区间里程段98+718至99+100地质信息如图1所示。新红区间表层有杂填土、素填土，其中以卵石和细砂为主，所穿越地层主要为中等风化泥岩和中等风化砂岩，以下简称泥岩和砂岩。区间段内泥岩和砂岩所占比例分别为41%和59%。其中泥岩天然密度均值为2.52 g/cm3，天然抗压强度标准值为6.35 MPa，内聚力均值为1.11 MPa，内摩擦角均值为26.75°；砂岩对应的指标分别为2.49 g/cm3、10.31 MPa、2.88 MPa和31.9°。

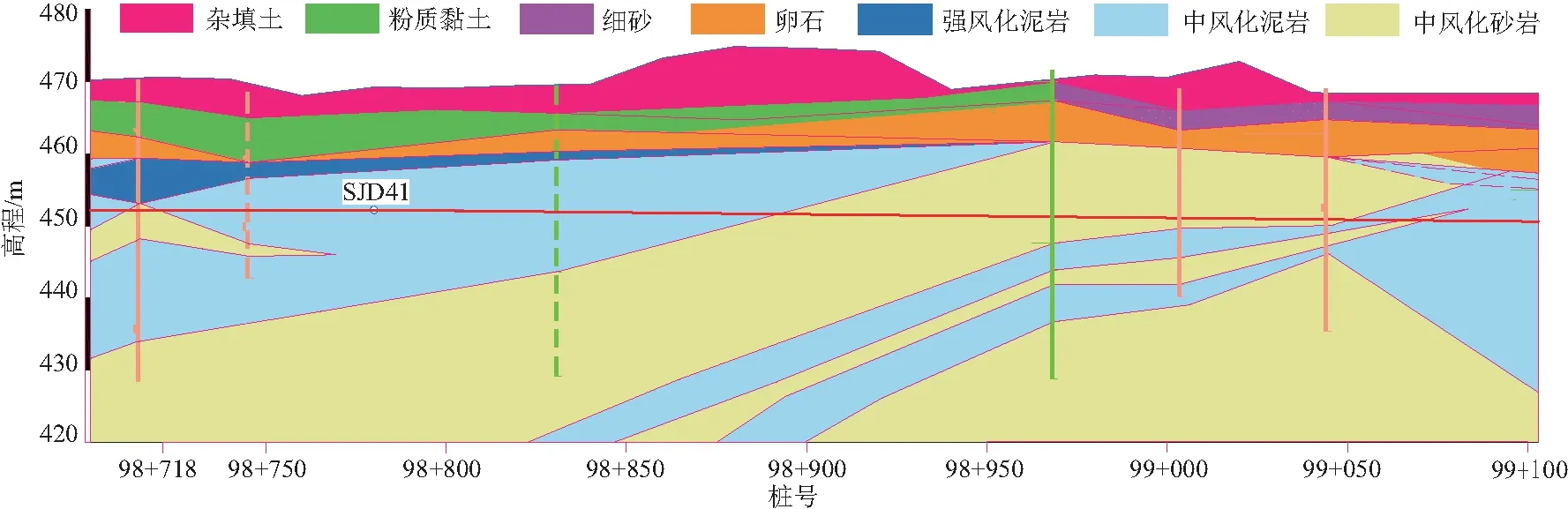
图1 新红区间地质信息Fig.1 Geological information of Xinmatou-Hongliancun segment

2.1.3 盾构设备

受泥岩和砂岩复合地层影响，新红区间采用中铁工程装备集团有限公司自主设计生产的EPB盾构机。设备运行数据按秒采集，以天为存储单位，详细地记录了包括刀盘推力、掘进速度、土仓压力、螺机转速等在内的530项掘进参数，总数据量高达38.5 GB。EPB设备的详细技术参数如表1所示。

表1 EPB主要技术参数Table 1 Main technical parameters of EPB

2.2 数据预处理

掘进机繁杂的数据类型和数据总量使得数据前处理面临更大的挑战，如何筛选出有效的学习数据成为要解决的首要问题。为此，提出了针对EPB掘进参数的标准预处理方案，该方案凝练为数据分割、异常值处理、数据降噪和数据编译4个阶段。数据分割、异常值处理、数据降噪过程如图2 所示。下面以掘进速度(V)为例详细说明数据预处理过程。

2.2.1 数据分割

EPB在存储有效数据的同时，产生了大量与破土掘进不相关的无效数据，如图2(a)红色虚线框所示。数据预处理的第一步便是将无效数据剔除，提取出有效数据(图2(a)绿色虚线框)。在推进系统推力和刀盘系统扭矩的联合作用下，刀盘上分布的滚刀或刮刀实现对岩土层的持续滚压、切削和剥落，当达到环片拼接长度后便停止破土掘进。上述过程可分为4个阶段：起始段(图2(b)“(1)”)、上升段(图2(b)“(2)”)、稳定段(图2(b)“(3)”)和结束段(图2(b)“(4)”)。单个掘进段具备以下典型特征：

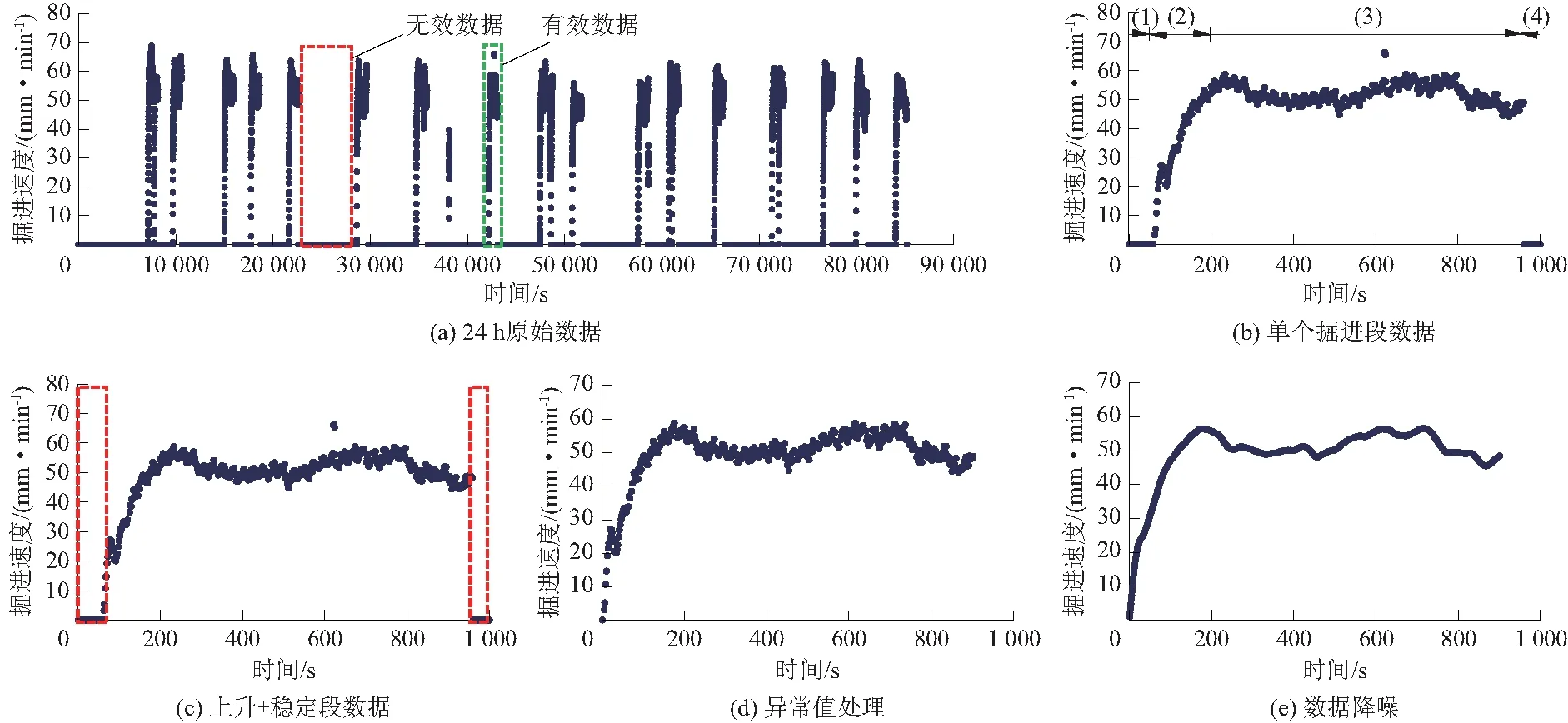
图2 EPB掘进参数预处理Fig.2 Preprocessing of EPB tunneling parameters

(1)有明显的起始阶段，此阶段司机启动刀盘系统，刀盘转速(N)和刀盘扭矩(T)由0逐渐增大，掘进速度(V)和刀盘推力(F)仍然为0。

(2)有明显的结束阶段，此阶段V和F几乎瞬间变为0，而设备的N和T缓慢降低至0。

(3)单个掘进段具有一定的掘进长度，从起始到结束掘进长度通常>0.1 m，小于管片长度的 1.2倍。

(4)相邻掘进段具有一定的时间间隔，上一掘进段结束和下一掘进开始，中间需要有用来出渣、拼装管片等工序的间隔时间。

根据上述特征开发了海量数据自动分割算法，可将图2(a)数据分割成独立的17个掘进段。单个掘进段的分割效果案例如图2(b)所示，其包含了完整的4个掘进阶段，数据为图2(a)绿色虚线框。值得注意的是起始段和结束段主要是EPB机器参数设定阶段，尚未正式开挖土层。因此，深度学习模型采用上升段和稳定段的数据(图2(c))。

2.2.2 异常值处理

由于EPB掘进时的参数记录均来源于自动采集系统，而该系统所处的工作环境是一个移动中且有较强振动和电磁干扰的环境，有时会造成传感器和采集系统本身所采集的数据信息明显超出合理范围(异常值)。目前，异常值常用的识别方法有箱线图、3σ法等[25-26]，处理方法有剔除、插值和均值替换等[27-28]。经过对比分析各种处理方法的优劣，最终采用3σ法识别异常值，掘进段均值替换异常值，处理结果如图2(d)所示。

2.2.3 数据降噪

异常值处理后，掘进参数在小范围内仍然有较大波动。已有研究表明这些波动会影响模型的训练过程，通过降噪可以提高模型的预测精度[29]。目前常用的去噪方法有傅里叶变换、低通滤波法和小波变换法等[30-31]。其中低通滤波法可将高频信号阻隔或减弱，最大程度达到降噪效果，具有处理速度快、原理简单等优点。为此，采用低通滤波法进行数据降噪，滤波器为Butterworth低通滤波器[32]，其表达式为

(1)

式中：|H(ω)|2为滤波器的平方幅度；n为滤波器的阶数；ωc为截止频率。

Butterworth滤波器的特点是通频带内的频率响应曲线最大限度平坦，响应幅度随着频率的增加而单调衰减，降噪的程度随着巴特沃斯滤波器阶数的增加而增加[32]。为达到良好的数据降噪效果，同时避免信息的丢失，通过试错法确定滤波器阶数为2，截止频率为0.2 Hz，V的降噪效果如图2(e)所示。

2.2.4 数据编译

数据编译工作便是从上亿条的掘进数据中筛选出有效数据，然后转换为可直观展示的.pdf格式文件。为生成可用于深度学习的标准盾构掘进数据集，首先将多个以天为单位的.csv格式文件合并为一个连续数据集，然后按照处理单个掘进段的方法对全部数据进行循环遍历，完成盾构数据的分割、异常值处理和降噪工作。最终生成用于可视化展示的.pdf格式文件和深度学习的.csv格式文件。

原始成都盾构掘进数据经过数据分割，共获得了1 905个掘进段，编号从00001至01905。

2.3 数据分析

2.3.1 相关性分析

经过数据预处理，盾构掘进数据总量下降，但其数据种类仍然繁多。因此，仍需从530项参数中筛选出与预测参数相关的输入参数。皮尔逊相关系数法(Pearson Correlation Coefficient，PCC)被用来提取与预测参数T和F具有高度相关的输入参数，其计算公式[33]为

(2)

式中：cov(x1，x2)为变量x1、x2的协方差；var(x1)和var(x2)分别为变量x1、x2的方差。

ρ(x1，x2)的正和负分别表示正相关和负相关；ρ(x1，x2)的绝对值越大表示输入参数与预测参数的相关程度越高。

图3为通过PCC法筛选出的与预测参数显著相关的输入参数，结果表明，推进压力(P)、V和N均与预测参数T和F有很强的相关性。EPB特有的掘进参数如螺旋机扭矩(Ts)和螺旋机转速(Ns)与T和F也具有较强相关性。另外，土仓压力(Cp)与T和F为负相关关系，即随着T和F的增大，Cp减小；Cp可用来评价开挖面的稳定性，并间接反映出T和F的变化趋势[34]。因此，上述6项掘进参数均作为模型的输入参数。

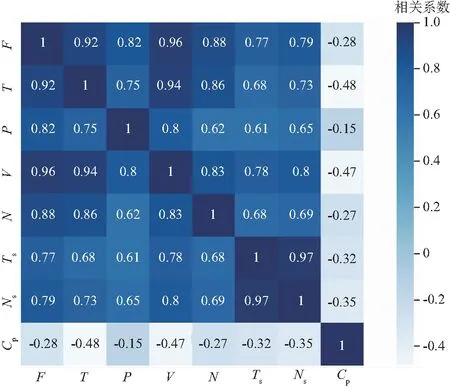
图3 掘进参数相关性分析Fig.3 Correlation analysis of tunneling parameters

2.3.2 预测参数分布特征

不同地层条件下预测参数T和F的频率分布直方图见图4。结果表明：参数T和F分布范围差距较大，参数F均值远大于参数T均值。另外，不同地层参数分布也有所差别，当EPB设备从泥岩地层掘进至砂岩地层时，参数T>80 kN·m所占比例上升，参数T均值从93.95 kN·m上升至104.90 kN·m。而砂岩地层中参数F<300 kN所占比例较大，导致参数F均值小于泥岩地层参数F均值。

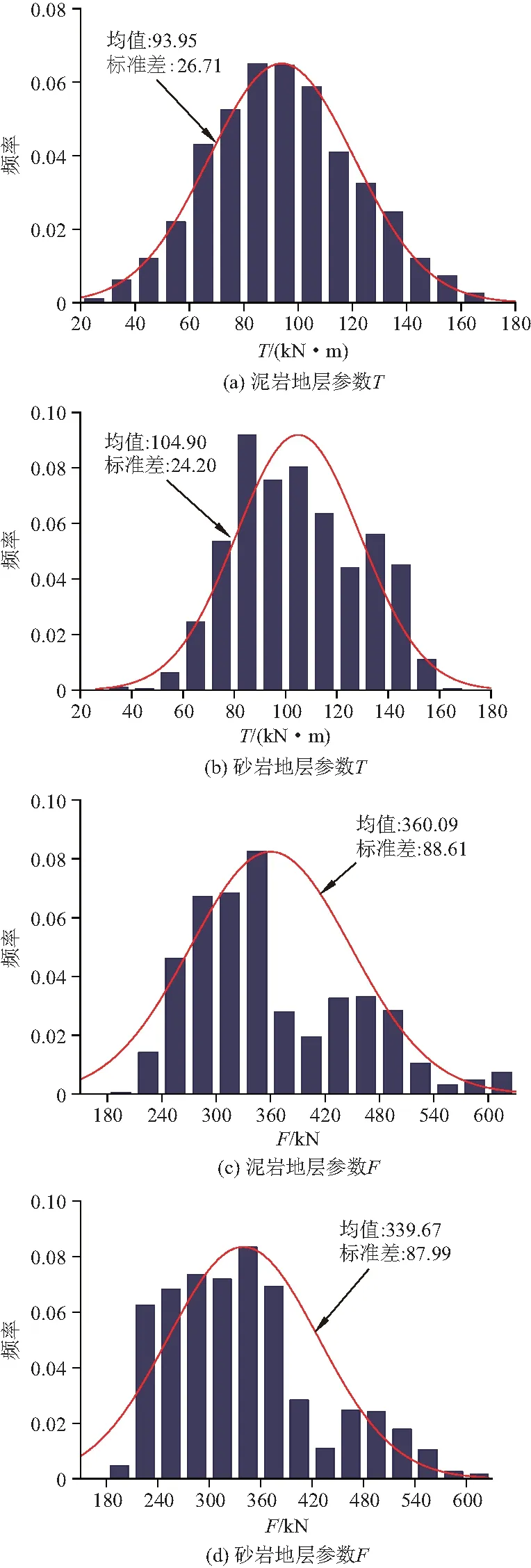
图4 频率分布直方图Fig.4 Frequency distribution histogram

3 模型搭建

3.1 GRU算法

GRU算法最早由Chung等[35]在2014年提出。相比LSTM算法，GRU同样可以解决RNN算法存在的长期记忆和反向传播中的梯度等问题，但其没有存储单元，运算和预测效率更高[35-36]。GRU单元只包含两个门——重置门和更新门，重置门决定了如何将新的输入信息与前面的记忆相结合，更新门定义了前面记忆保存到当前时间步的量。更新门和重置门的表达式定义如下：

zt=σ(Wz[ht-1，xt]+bz) ，

(3)

rt=σ(Wr[ht-1，xt]+br) ，

(4)

(5)

(6)

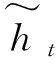
3.2 时序预测模型

掘进参数动态实时预测问题可转化为短时间序列预测问题，即回溯过去和当下若干掘进段的掘进参数信息预测下一掘进段的T和F，伴随着EPB向前掘进，数据序列不断滚动，实现动态预测。已有研究表明时序预测中预测参数的过去信息也是非常重要的参量[11-19]。因此，模型回溯的掘进参数除了掘进段P、N、V、Ns、Ts和Cp六个参数均值之外，还包括过去掘进段的T或者F均值。然后，将包含泥岩和砂岩信息的1 905个掘进段分为两组：第一组98+732至99+583里程段，共1 500个掘进段，约占总数据的80%，用于模型的训练；第二组99+583至99+865里程段，共405个掘进段，约占总数据的20%，用于模型的验证。另外，为消除输入数据的量纲差异，加快模型收敛，按Z-score标准化方法进行标准化处理，即

(7)

式中：u为数据样本均值；σ为数据样本标准差。

本文时序预测模型采用Keras模块中Sequential模块进行搭建，其结构如图5所示。模型结构包含一个输入层、一个GRU层、一个随机失活层、一个全连接层和一个输出层。首先将过去若干个掘进段的掘进参数输入到GRU层，GRU层从输入参数中提取特征后传输至全连接层；然后，中间的随机失活层可降低节点间的相互依赖性，增加模型的鲁棒性；最后全连接层将结果传递至输出层。同时为了降低输入参数的噪声信息，对输入层数据进行了Butterworth滤波处理，滤波的过程与2.2.3节的过程一致，这里不再阐述。

图5 基于Butterworth滤波的GRU模型结构Fig.5 Structure of GRU model based on Butterworth filter

3.3 评价指标

为评价模型的预测效果，本文采用均方根误差(Root Mean Squared Error，RMSE)和平均绝对误差(Mean Absolute Error，MAE)两个评价指标，其定义如下：

(8)

(9)

式中：n为样本总数；f(xi)为T或F的预测值；yi为T或F的实测值。

作为预测精度的指标，RMSE和MAE表示模型预测值与实测值之间的差异。如果这些指标足够小，就意味着预测值与实际值吻合良好。

4 预测结果分析

4.1 模型超参数分析

鉴于预测参数T、F分布范围有所不同，共训练了两个基于Butterworth滤波和GRU算法的模型，分别用来预测2种参数T、F。通过网格搜索确定了各个模型的最优超参数。图6为不同神经元个数、批量大小、回溯数据段和训练回合下99+583至99+715砂岩区域参数F的预测结果。

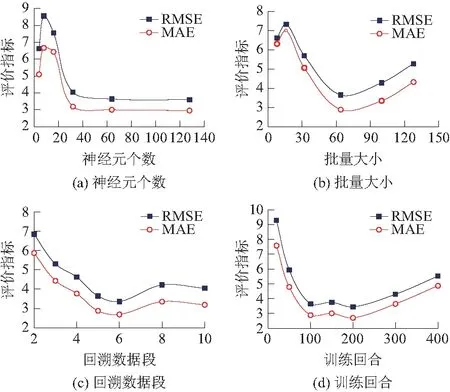
图6 不同超参数下模型对参数F的预测性能比较 (99+583—99+715)Fig.6 Prediction performances of model for parameter F under different hyperparameters (99+583—99+715)

如图6(a)所示，GRU层和全连接层神经元个数取值为32时，RMSE和MAE取得较低值，神经元个数增多，模型误差不再降低。同时，在批量大小为64时(图6(b))，模型取得最优预测效果。如图6(c)所示，当模型回溯数据量为5～6个掘进段时，模型有较好的预测能力，超过该范围后，模型的预测偏差增大。另外，图6(d)显示当训练回合为200时，模型基本达到最低误差。综上分析，最终确定的模型超参数见表2。

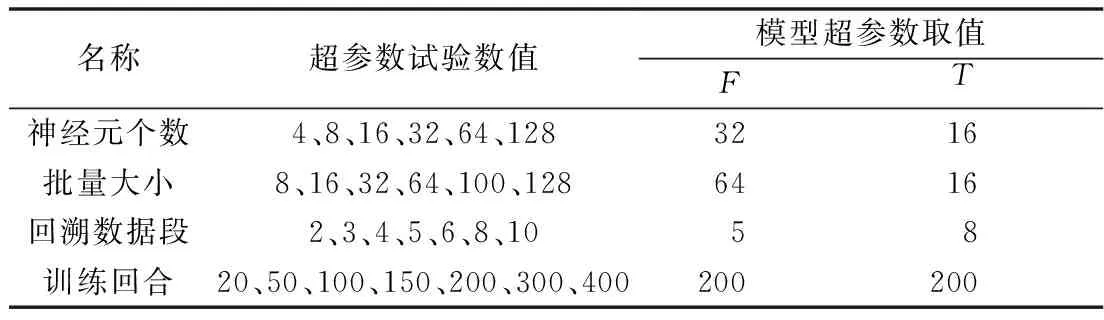
表2 GRU模型超参数取值Table 2 Hyperparameter values of GRU model

4.2 Butterworth滤波影响分析

图7对比了经过Butterworth滤波和未滤波模型对复合地层99+583至99+865掘进参数的预测效果。参数F和T预测结果表明，经过Butterworth滤波的模型(图7(b)、图7(d))在训练集和测试集上的预测效果均优于未滤波模型的预测效果(图7(a)、图7(c))。经过Butterworth滤波，参数F在测试集上的RMSE从17.78降低至11.19，MAE从 14.06 降低至8.44。参数T呈现类似规律，因此数据送入模型之前，对数据进行滤波是必要的。

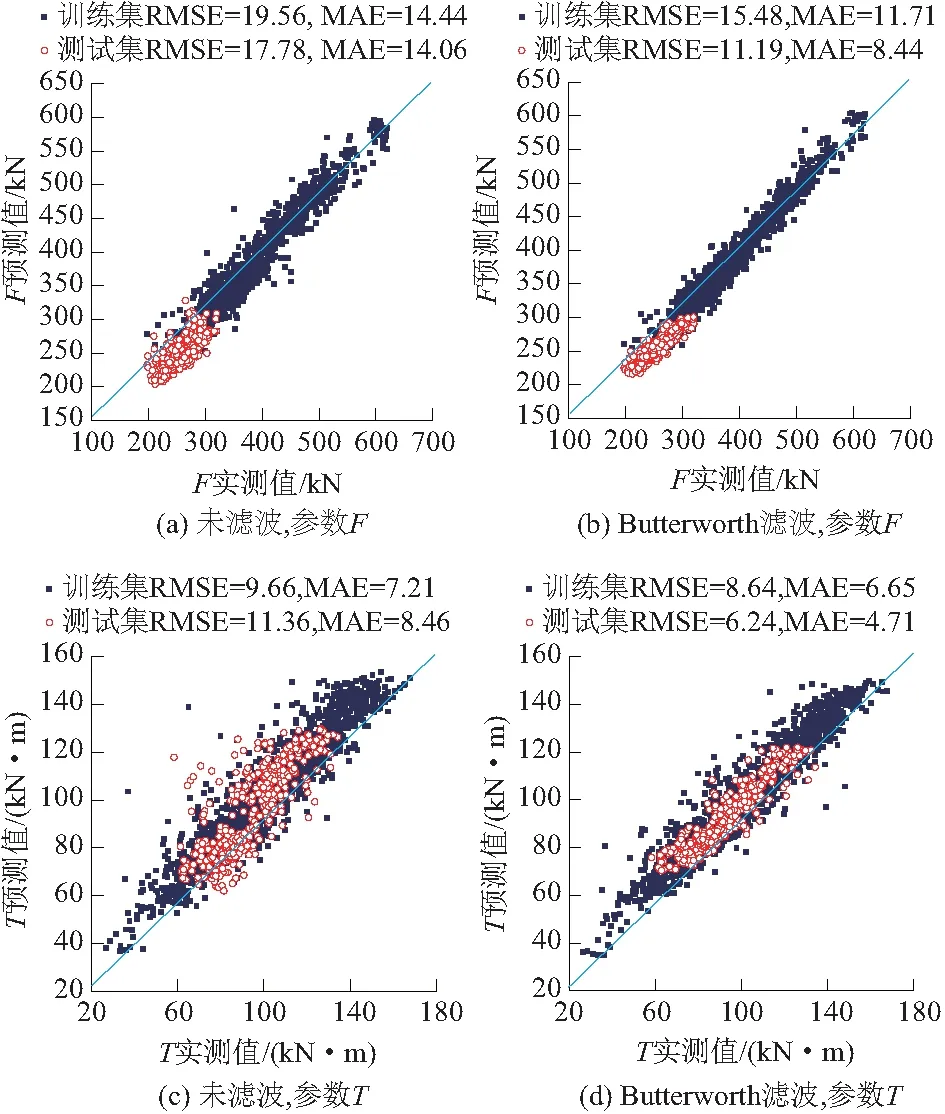
图7 Butterworth滤波对模型的影响Fig.7 Influence of Butterworth filter on the model

4.3 不同地层预测分析

测试集99+583至99+865里程段为泥岩和砂岩复合地层，模型对参数F和T的预测结果见图8和表3。结果表明，无论是泥岩地层还是砂岩地层，模型在测试集上的预测值与实测值均较接近。其中，模型对砂岩地层99+583至99+713里程段参数T的预测效果最好，RMSE和MAE分别为4.91和3.86。其他地层区间预测参数的RMSE均<13.0，MAE均<10.0。

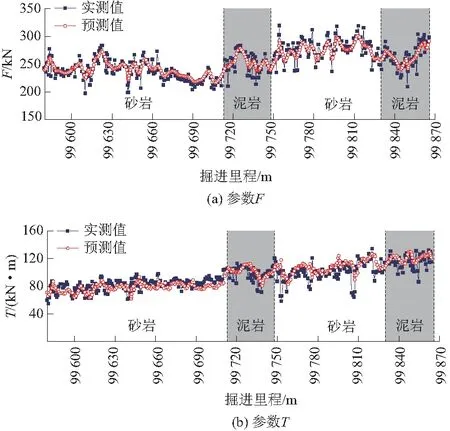
图8 模型预测结果Fig.8 Model prediction results

表3 GRU模型超参数取值Table 3 Hyperparameter values of GRU model

此外，原始实测值T和F受噪声信息干扰，经过Butterworth滤波的GRU模型预测结果可能更接近真实值T和F。综上，提出的GRU时序预测模型可用于EPB盾构机掘进参数的预测，可为之后掘进设备状态判断和参数优化调整提供基础。

5 结 论

基于成都地铁19号线二期工程土压平衡盾构机(EPB)采集的掘进数据，开发了海量数据标准预处理算法，筛选出了与预测参数相关的输入参数。在此基础上，建立了包含Butterworth滤波器和GRU算法的盾构掘进参数预测模型，主要结论如下。

(1)基于盾构大数据特点，开发了标准预处理算法，其包含数据分割、异常值处理、数据降噪和数据编译4个阶段，可实现提取有效掘进数据、修正异常值、滤除噪声和建立数据集4项功能。

(2)通过回溯过去掘进段的掘进参数，预测模型可有效地预测下一掘进段的T和F。预测模型在99+583至99+713里程段中对参数T取得了最低预测误差。

(3)T和F预测结果分析表明，超参数的调整直接关系到模型的预测效果；输入层数据进行滤波是必要的，经过Butterworth滤波的模型比未滤波模型的预测精度更高；模型对砂岩地层和泥岩地层均具有良好的预测精度。

本文所建立的预测模型可以为之后掘进设备状态判断和参数优化调整提供基础。另外，研究分析数据有限，有待进一步形成更多样化的数据库，以增强模型的稳健性。