面向长短期混合数据的MOOC辍学预测策略研究

杨坤融，熊 余，，张 健，储 雯

1.重庆邮电大学 通信与信息工程学院，重庆 400065

2.重庆邮电大学 教育信息化办公室，重庆 400065

在线学习被广泛认为是一场新的教育革命，已经成为教育学、心理学、数据科学等学科交叉研究的热门课题。在学术界和业界的共同努力下，尤其在新冠肺炎疫情突然爆发的刺激下，在线学习在教育中的作用越发凸显[1]。在此背景下大规模开放式在线课程（massive open online courses，MOOC）提供数千门精心设计的在线课程，充分满足数以万计学生的需求。在一个典型的在线学习平台中，学生不仅可以自由地访问课程视频，完成作业和参加考试，还可以使用在线论坛和维基等辅助工具。显然，在线学习因为优质、开放、免费等诸多优点而广受学生的青睐，但需要注意的是，由于师生缺少面对面交流，学生上课时间碎片化等问题，在线学习具有极高的辍学率[2]。相关研究表明，大多数在线学习平台的课程完成率低至4%～10%，而辍学率高达80%～95%[3]。同时，由于在线学习环境中教师相比于学生数目较少，教师无法跟踪每一位学生的学习行为。因此，对学生进行精准和及时的辍学预测，从而提高在线课程的保留率，改善在线课程质量和教学方法对在线学习的持续健康发展具有重要意义[4]。

高辍学率对MOOC 平台和学生自身都有负面影响，不利于MOOC 在全球的持续发展。从平台角度来看，辍学会增加每个学生的平均成本，因为吸引新学习者的注册成本远大于留住潜在辍学者的成本。而从学生角度来看，辍学是对时间和精力投入的浪费。为了解决高辍学率这一显著问题，就必须充分利用MOOC 平台中记录并储存的海量学习者行为数据建立预测模型，实现对辍学者的精准预测。辍学预测是根据学生历史学习行为记录来预测未来某个时间退出课程的可能性[5]。通过对学生行为建模预测辍学概率，可以随时获取学习者在平台的学习情况，提前发现其辍学风险。MOOC平台存储的学习行为数据主要包括点击流数据、论坛数据和作业数据三大类，研究者通过制定合理的特征工程，从这些行为数据中提取影响学生最终学习效果的特征，以便进一步建立辍学预测模型。其中点击流数据因能较完整地反映学生的学习轨迹，在构建辍学预测模型时往往能取得较好的性能[6]。现有的辍学预测方法主要使用传统机器学习算法和深度学习算法建立预测模型，从而提高预测的准确性。文献[7]将学生的每周学习行为形成序列，根据每周学习行为情况定义不同类型的学生，使用支持向量机（support vector machine，SVM）构建模型预测学生下周的辍学情况。文献[8]从点击流数据中提取学生行为特征，综合运用逻辑回归（logistic regression，LR）和线性SVM 方法预测辍学行为，并在预测过程中对每个特征向量做辍学预测性的检验，得出在前几周预测中加入论坛数据能有效提高预测准确率。文献[9]提出一种基于长短期记忆（long shortterm memory，LSTM）网络的辍学预测策略。首先将辍学预测问题视为时间序列预测问题；随后将学生点击流和论坛数据以周为时间步长构建学生行为时间序列，最后利用LSTM预测学生是否辍学。文献[10]以卷积神经网络（convolutional neural networks，CNN）作为预测模型，并设计了一个基于时间序列的二维矩阵作为输入，将时间信息与学生的行为特征相结合，解决了行为特征之间的短期依赖性问题。文献[11]综合考虑了CNN 和LSTM 的优点，提出了一种CLMS-Net 混合网络结构。该网络由CNN、LSTM 和SVM 组成，其中CNN 可以从学生行为数据中自动提取有用的特征，LSTM用于捕获学生行为数据中的时间关系，SVM 作为最终的分类器判定学生是否辍学。

虽然以上研究已经取得了比较好的表现，但仍然存在两方面问题：（1）当前研究忽略了学生行为数据的短期依赖关系以及长期的模式和趋势。MOOC 课程往往会持续数周，在课程学习期间学生的行为活动以周为单位分布得非常均匀，此时学生行为序列不仅呈现短期的依赖关系，而且存在长期的周期性，传统的机器学习算法和常用的CNN、LSTM等深度学习算法并不能很好地捕捉数据的这些特点[12-13]。（2）当前研究在辍学预测中默认为辍学和不辍学样本的数量差别不大，忽略了辍学预测中的动态类别不平衡问题。实际上，尽管在线学习平台的总体辍学率较高，但在课程学习过程中的每一时间步长下（如每周），辍学的学生相比于未辍学的人数仍然较少，数据集随着课程的开展不断变化，同时存在类别不平衡问题。并且在训练模型时先前研究通常假设数据集中辍学和未辍学两类样本误分类代价相等，以整体误差最小化为目标训练预测模型。故在此情况下预测模型分析得到的结果会偏向多数类，即未辍学的学生，从而使得实际上要辍学的学生被模型判定为未辍学，无法及时进行人为干预，造成学生放弃课程的后果。

为此，可将MOOC 辍学预测视作长短期不平衡时间序列问题，提出一种针基于深度学习的辍学预测策略（dropout prediction strategy based on deep learning，DPSDL）。该策略首先构建以天为时间步长、周为学习周期的新型学生行为时间序列；然后结合两种不同的辍学定义，判断不同时间点学生的辍学人数并揭示辍学预测中的类别不平衡现象；随后为了捕捉学生行为数据长期的模式趋势和短期的依赖性，使用长短期时间序列网络（long-and short-term time-series network，LSTNet）构建时间序列预测模型，该模型中的卷积单元用于捕捉学生行为中的短期依赖关系，并且通过循环跳跃层对输入数据进行维度整理，缓解网络中的梯度消失现象，以此获取数据中更为长期的模式和趋势，并充分利用时间序列的周期特性；最后引入代价敏感性学习解决不同时间步长下的动态类别不平衡问题，提升预测精度。

1 问题描述

1.1 辍学预测中的时间序列

MOOC 平台上教学形式通常是教师每周将课程内容以在线视频的方式发布给学生，并且教学者会布置一些作业供学生作答。随着课程的进行学生可能会对课程的某些内容和作业存在疑惑，这时可以去课程对应的论坛讨论问题，MOOC平台会记录课程中所有学生的学习行为。本文对学生的学习行为进行分析，深度挖掘学生的学习规律，新发现了学生行为记录数据的长短期混合模式。一般地，以一周为时间步长可将学生每周在平台上的所有活动数据汇总开展学习分析。通常，每周学生会按照某种长期养成的学习习惯和规律开展学习（例如在每周初首次观看课程视频而在本周末课程结束时完成作业），这使得学生行为随着课程的进行呈现长期的周期性[14]。同时，学生的学习行为并不是独立出现的，而是在某段较短时间内连续发生（例如学生在完成作业前会再次观看课程视频并浏览课程论坛），因此学生行为也存在短期依赖关系。要捕捉学生行为数据的长期模式趋势及短期依赖性，通常以周为时间步长的学习分析将难以准确描述这种复杂的时间序列关系。为此，这里将时间步长缩小为一天，并以一周为一个学习周期，由此捕捉每一时间步长下时间序列数据的短期依赖关系和相邻学习周期之间的长期模式和趋势。将学生K周的学习行为按时间顺序形成序列XK=(x1,x2,…,xt,…,x7K),其中xt为第t个时间步长下的行为序列。同时，可根据所采用的辍学定义为每个学习周期各个学生生成一个辍学标签，这里yK∈{0,1}（0代表未辍学，1代表辍学）。随着课程的推进，辍学预测问题可以定义为：使用学生截至第K个学习周期（包括第K个周期）的行为序列XK，从而预测学生在该周期结束时的状态yK，在每个学习周期结束时预测一次，直到课程结束，如图1所示。

图1 学生长短期时间序列构建Fig.1 Construction of students’long-and short-time series

1.2 辍学预测中的动态类别不平衡问题

在MOOC辍学预测中的动态类别不平衡问题是指数据集中每个时间点未辍学人数远高于辍学人数，并且类别的数量随时间不断发生变化，本文揭示了这种现象。为了准确认识这个问题，首先依据辍学定义判定学生在某个时间点是否处于辍学状态，随后统计该时间点的辍学人数和未辍学人数，最后通过计算不平衡率（imbalance ratio，IR）衡量数据集的不平衡程度[15]。IR可由式（1）计算得出：

其中，n1和n2分别为辍学和未辍学的人数。若IR＞1,即n2＞n1，说明未辍学人数多于辍学的人数，且IR值越大，学生辍学预测中的类不平衡程度越高，反之则越低。

为了判定学生在不同时间步长的状态，需要应用准确的辍学定义判断学生是否辍学。为了证明类别不平衡现象并不是偶然发生，这里使用MOOC 辍学预测研究通用的KDD Cup 2015数据集，结合文献[16]总结的两种最常用的辍学定义判定数据集中学生在不同时间步长的状态。

辍学定义1：若(xt+1,xt+2,…,xt+m)=∅,即学生在未来一段或多段时间步长内没有学习行为，则判定为辍学。

辍学定义2：若a∉(x7K-6,x7K-5,…,x7K),即学生在课程结束之前的最后一周内没有提交作业的行为，则判定为辍学。其中a为提交作业行为。

根据学生学习课程的不同阶段，可结合以上两种辍学定义来分析其辍学行为，其中定义1 和定义2 分别适用于课程前中期和末期。按照第1.1节提出的学生行为时间序列，从KDD Cup 2015公开数据集中选择人数较多的5 门课程[4]，统计在每个学习周期结束后辍学人数和未辍学人数，并计算不平衡率IR。对于辍学学生只统计本学习周期结束时新产生的辍学人数，而不是累计的辍学人数。图2 是数据集不平衡率变化情况，图3 为在线课程人数随时间变化示意图。从图中可以看出，随着课程的开展，不断地有学生放弃课程，在每个时间段辍学的人数实际上少于未辍学的人数，是一个累积的过程，因此辍学者应当视为少数类，而未辍学者为多数类，并且数据集的类别不平衡程度随着时间的推移动态变化。许多学生选择在课程的第一周放弃课程，此时数据集不平衡率IR较低。随着课程的开展，辍学人数不断下降，课程人数较为平稳，所对应的数据集不平衡率IR逐渐上升，在第3周达到峰值（最高为8.82），最后在第5周达到最低点（最低为0.75），并且大多数时间段的IR皆大于1，数据集存在动态类别不平衡问题。在课程第1周学生处于课程的初步了解阶段，由于课程内容不合适或难度较高，导致辍学人数较多，此时IR并不高；随着时间的推移，课程逐渐进入平稳阶段，只有少部分学生辍学，因此数据集极度不平衡；在课程最后1周，学生面临考试的压力，也有一部分学生参加课程的目的是学习课程内容，对于最终的考试成绩并不关注，因此导致辍学人数急剧上升，从而降低了IR。可见，课程在线学习人数是不断变化的，因此数据集的不平衡程度随着课程的推进而不断起伏，且在大多数情况下类别不平衡问题较为严重，即在一个学习周期内未辍学学生的数量远大于辍学学生。

图2 不平衡率随时间变化情况Fig.2 Imbalance ratio changes over time

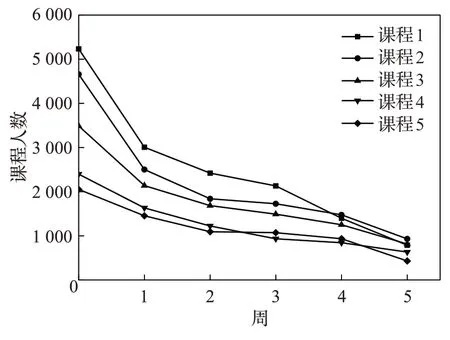
图3 课程在线学习人数变动示意图Fig.3 Illustration of change in the number of online learning students

2 预测模型

从以上分析可知，通过统计分析时间序列数据的特点，可将MOOC 辍学预测视为长短期不平衡时间序列分类问题。目前深度学习算法已经成为构建时间序列模型的主流工具，现有研究所使用的深度学习模型可分为三类：（1）单一的CNN；（2）单一的RNN 及其变体，例如LSTM 和GRU；（3）由CNN 和RNN 组成的混合神经网络。其中，CNN 虽然能够通过滑动卷积核窗口以及池化等方法捕捉时间序列数据中的短期依赖关系，但是由于其卷积核大小的限制，不能很好地抓取长时的依赖信息。而以LSTM和GUR为代表的循环神经网络由于训练的不稳定性和梯度消失问题，很难记录较为长期的周期模式[17]。因此本文充分考虑辍学预测数据集中学生行为的短时间连续性和长期周期性，引入LSTNet 网络作为预测模型解决学生时间序列数据中短期和长期混合模式的捕获问题，其核心思想是充分发挥CNN 的优势，发现短期连续行为之间的局部依赖模式，并通过特殊的循环层对输入数据进行维度整理，缓解深层网络中的梯度消失现象，达到获取学习行为中更为长期的模式和趋势的目的，并充分利用学生行为的周期特性[13]。如图4所示，LSTNet由卷积单元、循环单元、循环跳跃单元以及密集层组成。学生行为时间序列首先输入卷积单元中，用于提取每一时间步长下学生行为之间局部模式和短期依赖关系；随后，将卷积单元的输出分别输入到循环单元和循环跳跃单元中，用于发现相邻学习周期间数据的长期模式和趋势；最后，通过密集层整合循环单元和循环跳跃单元的输出，并得到最终的预测结果。

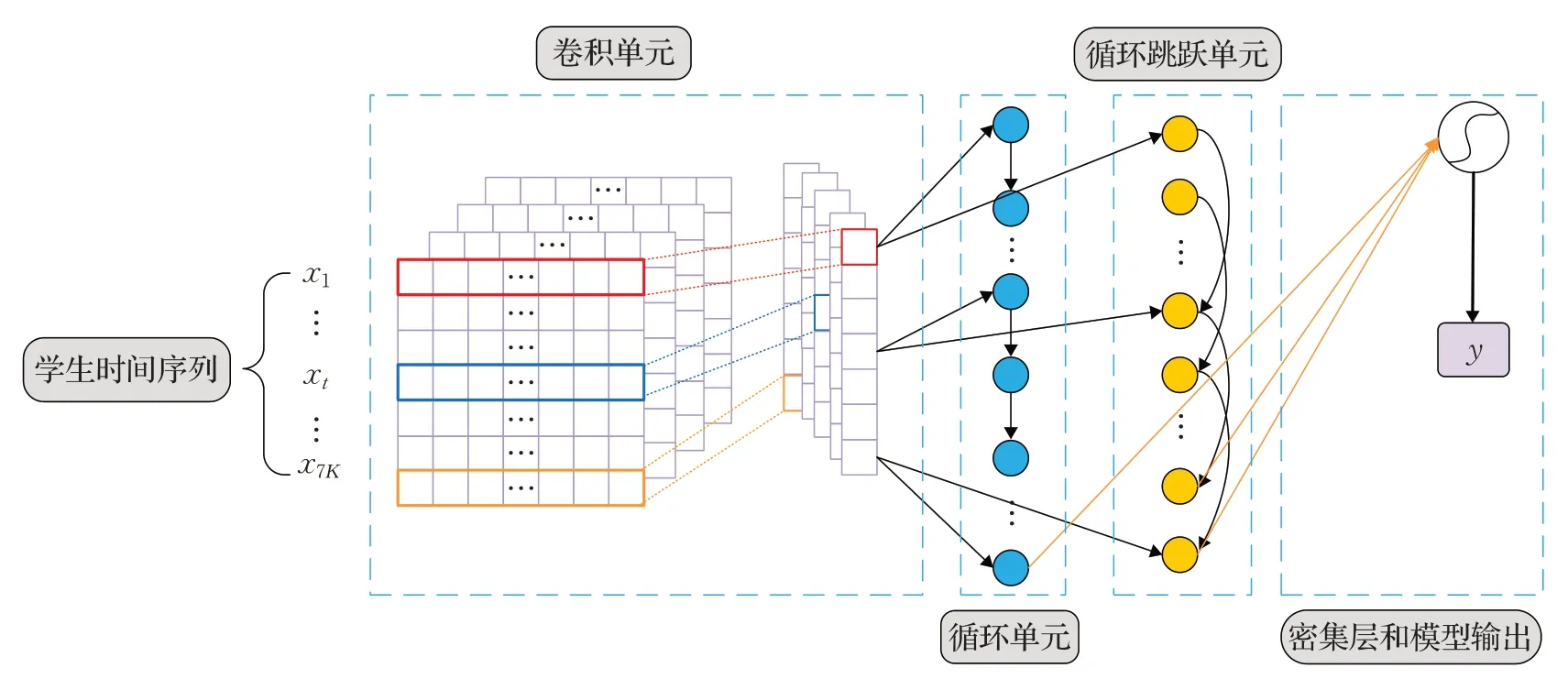
图4 LSTNet网络预测模型Fig.4 LSTNet network prediction model

2.1 卷积单元

LSTNet的卷积单元是一个不含池化层的单层卷积神经网络。学生MOOC 平台在每一次学习中，往往会在一段较短的时间进行多次学习活动，例如观看学习视频、查找资料、参与讨论等。因此可以通过卷积单元提取每一时间步长下连续学习行为之间的局部相关性信息，并获得与辍学相关的高级特征。这里使用前面图1所设计的学生行为序列X=(x1,x2,…,xt,…,x7K)作为模型输入。为了加快模型的收敛速度，缓解深层网络中“梯度消失”的问题，学生行为序列X经卷积层处理后需要进行批量归一化（batch normalization，BN）才能输入到ReLU激活函数中[18]，如下所示：

其中，W为权重矩阵，*为卷积运算，b为偏置，s、y、D分别为卷积层输出、批量归一化输出和卷积单元的输出。

2.2 循环单元

卷积单元的输出D=(d1,d2,…,dq)同时输入到循环单元和循环跳跃单元用于捕获学生时间序列学习周期之间的长期模式，其中dq为第q个卷积核的输出。循环单元由基于门控循环单元（gated recurrent unit，GRU）的循环层构成，学生经常在连续多个时间步长内表现出相似的学习行为，即学生在第二天的学习状态有很大的可能性与学生前一天的学习状态相似，因此可通过GRU记忆模块中的更新门与重置门两个门函数对学生行为之间的时间信息进行进一步提取。更新门用于控制前一时间步长的状态信息被带入到当前时间步长中的程度，权值越大表明前一时间步长的信息带入越多，学生在相邻时间步长之下学生状态越相似，学习存在规律性；重置门用于控制忽略前一时间步长的状态信息程度，其权值越小说明忽略得越多，学生某些偶然或无关学习行为越多。第t个时间步长下GRU记忆模块的门函数计算公式如下：

更新门rt：

重置门zt：

更新规则ht：

其中，Wr、Wz、为权重矩阵。

2.3 循环跳跃单元

MOOC 平台的教学视频和作业测试等课程资料一般每周组织一次，在课程期间学生的行为活动以周为单位分布得非常均匀，因此学生行为序列呈现长期的周期模式。但是GRU和LSTM神经网络由于“梯度消失”问题很难捕捉这种长期的周期模式，因此LSTNet 通过在循环单元后添加循环跳跃单元来解决这个问题。循环跳跃单元主要是在循环单元上做出修改，即相对于GRU和LSTM，循环跳跃单元中隐含层与一个周期之前时刻的隐含层建立联系，而不是前一时刻的隐含层，在学生长期的学习行为之间建立联系，获取学习行为之间的长期相关性，捕获其周期规律。如下所示：

更新门rt：

重置门zt：

更新规则ht：

其中，p为跳跃过的循环神经元的数量，由于定义的时间步长为一天，一周为一个周期，这里p=7。随后使用一个密集层组合循环单元和循环跳跃单元的输出，将循环单元在第t个时间步长时刻下的输出定义为，循环跳跃单元从第t-p+1 至t个时间步长时刻的定义为，密集层的输出可以表示为：

3 代价敏感性学习

先前研究在训练辍学预测模型时，通常假设数据集中辍学和未辍学两类样本误分类代价相等，以整体误差最小化为目标更新模型参数。然而在MOOC辍学预测中辍学样本相比于未辍学样本拥有更高的重要性，例如将一个高辍学风险的学生判定为未辍学时，教师则可能不会给予帮助，从而导致学生放弃课程的后果，而将无辍学或低风险的学生判定为辍学时，教师的介入并不会产生消极影响，因此辍学样本的误分类代价应比未辍学要高，而不是相等。并且随着课程的开展，如前面图2和图3所描述的动态类别不平衡现象，这时分类误差主要来自未辍学学生，在这种情况下以整体误差最小为目标训练模型，会导致预测模型偏向于未辍学而忽略辍学，造成无法正确识别辍学学生的后果。

代价敏感性学习以代价敏感理论为基础，将分类的重心放在误分类代价较高的样本，以不同类别样本误分类总代价最低为优化目标。因此本文引入基于代价敏感性学习的全局均方误差分离（global mean square error separation，GMSES）算法[19]，优化LSTNet 预测模型，将深度学习算法和代价敏感性学习结合，获取学生行为记录数据中长短期混合模式的同时，解决数据集中的动态类别不平衡问题。该方法通过分离各个类别的分类误差，并赋予不同的代价权重，以保证不平衡数据中多数类与少数类的分类精度。GMSES算法使用的损失函数如下：

其中，c为训练集样本的数量，ec和yc分别为模型的期望输出和实际输出，k为代价权重，当样本为多数类时（未辍学）k=1，当样本为少数类时（辍学）k=k*。由于MOOC 数据集的不平衡率IR随着课程的进行动态变化，k*也应该随着数据集的变化而拥有不同的最优值。为此，这里可使用梯度下降法来优化k*，使其基于每一批次训练的几何平均数（geometric mean，G-mean）和精度（Accuracy）而自适应变化，并使用梯度下降进行优化，如式（15）～（18）所示：

式（15）为k*的损失函数；T为每一批次训练集少数类最大误分类代价；H为完整数据集的少数类样本的最大误分类代价（这里设为训练集的不平衡率IR）；式（18）为梯度下降算法的更新步骤。伪代码如算法1所示。

该算法的步骤1～4为训练前的准备工作，对数据集进行划分，并将模型的权重ω*、偏置b*和少数类样本的代价权重k*进行初始化，随机生成初始值。步骤6～11为LSTNet的迭代训练过程，在每一次迭代下，首先需要将划分后的数据集vi依次输入模型中，随后基于式（14）的损失函数对模型进行训练，最后更新模型权重ω*和偏置b*。步骤12～14为少数类样本代价权重k*的计算过程，每一次模型迭代训练完成后，需要对权重k*进行计算并更新，直到迭代次数达到上限。

4 实验分析

4.1 数据集描述

KDD Cup 2015 数据集是教育数据挖掘领域应用最为广泛的数据集。由于在线教育平台的盈利性，目前极少有完整并且真实的公开数据集，数据集极其稀缺。因此KDD Cup 2015 数据集有极高的研究和应用价值。该数据集记录了“学堂在线”2013 年10 月27 日至2014年8月1日期间学生的课程选择记录和学习记录，共有来自39 门课程的79 186 名学生的120 542 条注册活动日志，每门课程需要长达5周的学习时间。经过对数据集的分析，只有5%～10%的学生会参与论坛，大多数学生没有任何的论坛行为数据。因此这里不将论坛特征作为预测特征，只采用点击流数据和作业数据来进行辍学预测。由于同一学生在不同课程之间辍学行为具有相关性[5]，为了进一步提升预测精度，将学生在其他课程的行为也作为预测特征。例如预测学生在课程c的辍学情况，将学生在除课程c外的所有课程的点击流数据和作业数据的平均数、最大值和最小值也作为预测特征。完整的预测特征如表1所示。

表1 第t 个时间步长下学生在课程c 的特征列表Table 1 Feature list of students in course c at t-th time step

4.2 参数设置、对比策略及评价指标

实验采用Anaconda3.50 作为仿真平台，LSTNet 的输入为第1.1 节所建立的学生时间序列矩阵，卷积单元为单层的一维卷积，使用100 个卷积核生成100 个特征映射，卷积核大小均为6。循环单元和循环跳跃单元中神经元数目为100，并使用Dropout 函数防止过拟合现象，取值为0.2。模型最终输出为0～1的数字，表示学生在相应课程辍学的概率。其中大于0.5 则定义为辍学，反之则为未辍学。使用代价敏感性学习训练模型时，批量大小设置为32，迭代次数设置为200。

本次实验从KDD Cup 2015数据集中选择15门课程，每门课程持续时间为5周，即为5个学习周期。在每个学习周期结束后，使用第1.2 节提出的辍学定义对数据集中辍学样本和未辍学样本进行更新，并将数据集中的80%的学生数据作为训练集，其余20%作为测试集，实验的基线模型为SVM[7]、LR[8]、梯度上升决策树（gradient boosting decision tree，GBDT）[21]、朴素贝叶斯（naive Bayes，NB）[22]、LSTM[9]、CNN[10]和CLMS-Net[11]。

常规的评价指标一般使用精度和AUC，但在MOOC辍学预测中，数据集的类别不平衡问题使得辍学样本在一个学习周期内远少于未辍学样本，因此辍学样本对总体的预测精度影响较小，这导致即使将全部学生样本视为未辍学，模型依然被认为拥有较好的性能。为此，所选用的评价指标需要适用于类别不平衡数据集的特点。本文除了选择精度和AUC 两种常用评价指标，并且挑选针对不平衡数据分类性能评估的两种典型评价指标，分别是F1值和G-mean，如下所示：

其中，TPrate为真正率，表示正类样本中被正确分类的概率；TNrate为真负率，表示负类样本中被正确分类的概率；precision为查准率，表示预测为正类的样本中被正确分类的概率。F1 是基于查准率和真正率的调和平均，用于衡量模型对辍学样本的分类性能；G-mean结合了辍学样本和未辍学样本的分类准确性，用于衡量模型对数据集整体的分类性能。TPrate、TNrate和precision的定义如下：

4.3 整体性能对比

第一次对比实验，将基线分为两类，分别为传统机器学习算法（traditional machine learning algorithms，TA）和深度学习算法（deep learning algorithms，DL）。传统机器模型包括SVM、LR、BDT、NB。深度学习算法包括CNN、LSTM 和CLMS-Net。统计传统机器学习算法和深度学习算法在精度、AUC、F1值和G值的整体表现，并与所提DPSDL 策略进行对比，其中DPSDL-W 表示所提策略不使用代价敏感性学习进行优化。第一次实验目的是验证通过捕获学生行为数据的长短期混合特性能够提升预测精度。实验结果如图5所示。

图5 显示了在第一次比较实验中不同策略精度、AUC、F1值和G值的整体表现。其中DPSDL-W表示所提策略不使用代价敏感性学习。结果表明，在连续时间步长下，以SVM、LR、BDT 和NB 为代表的传统机器学习整体表现最差，而可以获取学生学习行为之间依赖关系的深度学习策略和所提的DPSDL-W 策略能获得比传统机器学习更高的准确性。在第1 周时，DPSDL-W和深度学习在四种评估标准下的整体表现差距并不大。这是由于此时学生行为记录只包含一个学习周期的数据，学生行为数据并没有呈现周期性，导致所提DPSDL策略使用的LSTNet模型的循环单元和循环跳跃单元无法捕捉相邻学习周期之间的关系，其模型的优势未得到充分展现。随着课程的推进，学生行为记录逐渐包含多个学习周期，所提DPSDL-W 策略性能不断上升，明显优于深度学习策略，其精度、AUC、F1 值和G 值比深度学习策略平均提升了5.5%、6.4%、4.9%和6.8%。原因是深度学习算法中的CNN虽然通过滑动卷积核窗口以及池化等方法能够捕捉时间序列数据中的短期依赖关系，但是难以捕捉长期的周期模式。LSTM和CLMS-Net由于梯度消失问题，无法提取学生行为数据中较为长期的周期模式。而本文所使用的LSTNet 不仅充分发挥了CNN的优势，捕捉学生行为数据中的短期依赖关系，同时通过循环跳跃层对输入数据进行维度整理，缓解网络中的梯度消失现象，以此获取更为长期的模式和趋势，并充分利用学生行为数据的周期特性。从以上分析可知，所提策略在不同时间点均取得了优异的性能，因此通过构建长短期学生时间序列，并引入LSTNet 网络模型能够解决学生行为数据的长短期混合特性的捕获问题，提升预测精度。同时也注意到，在课程第3周，所提三种策略的整体表现均有所下降，如第3周的DPSDL-W策略的精度、AUC、F1 值和G 值相比于第2 周分别下降了1.4%、3.5%、0.9%和1.8%。因为此时处于课程中期，学生的学习状态较为平稳，辍学人数远少于未辍学人数，使得数据集中类别不平衡问题极为严重（正如图2 所示），从而导致预测性能变差。

图5 不同类型策略的整体性能Fig.5 Overall performance of different types of strategies

4.4 代价敏感性学习性能对比

第二次对比实验是将CNN、LSTM 和CLMS-Net 三种深度学习策略和DPSDL-W 使用代价敏感性学习进一步优化，证明代价敏感性学习可以解决辍学预测中动态类别不平衡问题，达到提升预测精确度的目的。如图6所示，CS-CNN、CS-LSTM、CS-CLMS-Net为使用代价敏感性学习优化后的深度学习策略，DPSDL 为所提的完整策略。可以看到优化后的三种策略性能均有明显提升，其中精度平均提升了1.6%，AUC值平均提升了2.2%，F1 值平均提升了1.94%，G 值平均提升了1.91%。尤其在动态类别不平衡问题最严重的第3周，性能提升最为明显，其中四种评估标准分别平均提升了2.3%、3.9%、3.76%、3.1%。而所提完整的DPSDL 策略的性能仍然优于三种深度学习策略，其精度、AUC、F1 值和G值分别提升了1.36%、2.28%、1.38%和1.94%。因此，引入代价敏感性学习可以在原有策略基础上提升预测性能，达到解决数据集中的动态类别不平衡问题的目的。

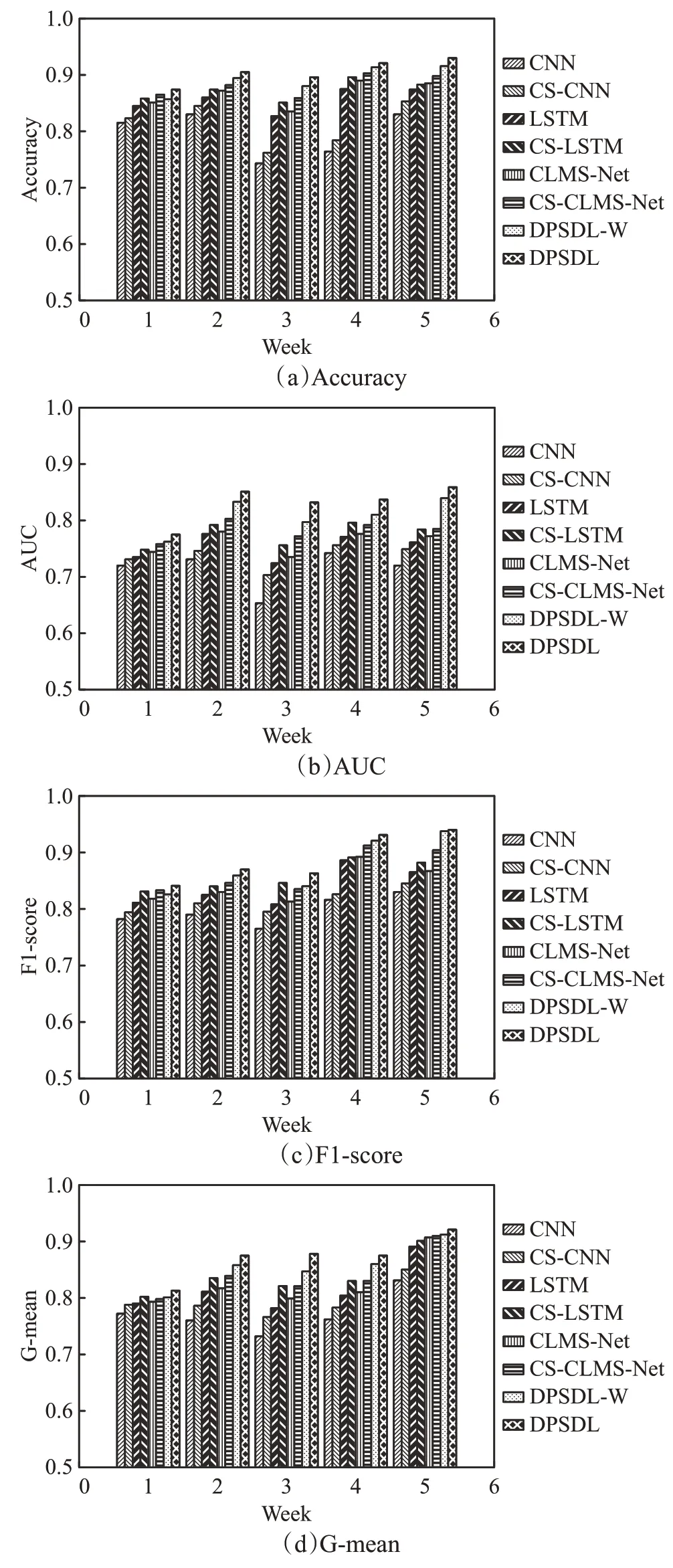
图6 代价敏感性学习性能对比Fig.6 Cost-sensitive learning performance comparison

综上所述，所提DPSDL 策略通过捕捉学生行为数据中的长短期混合特性和解决类别不平衡问题，提升了在课程不同阶段对辍学学生的预测能力，在不同时间点均取得了良好性能。该策略可以帮助教师解决课程不同阶段的监控、预测问题，提前预测辍学时间点和有辍学风险的学生，使教师能够及时采取有针对性的课程设计和向此类学生提供个性化的干预措施提升MOOC保留率，提高学生学习效率与课程质量。并且通过引入代价敏感性学习解决预测中的动态类别不平衡问题，提高模型对辍学者的识别能力，避免对辍学者的错误识别导致无法获得教师的帮助和干预而退出课程的后果。从先前分析可知课程第1周和最后1周对于学生是最具有挑战的阶段，容易导致较高的辍学率。原因为学生在第1周多数处于尝试状态，若有课程难度过高、内容不适合等原因，就会使其直接放弃该课程；在课程中期，课程进入相对平稳的阶段，多数学生的学习步入正轨，此阶段辍学人数较少；而在课程最后1 周，学生面临期末考试的压力选择辍学，也有一些学生由于更关注课程的内容而对成绩并不在乎，主动放弃课程。因此在课程第一周教师如果能够及时对学生进行有针对性的教学和辅导，将有助于学生进入学习平稳阶段。而在最后一周，如果能够采取鼓励学生参加最终的考核策略，则可以有效降低最终辍学率。

5 结束语

本文针对MOOC学生时间数据混合长期和短期两种模式以及辍学预测中的类别不平衡问题，提出一种基于深度学习的辍学预测策略。首先从学生学习活动日志中，以一天为时间步长，一周为一个学习周期构建学生时间序列；随后使用LSTNet网络作为预测模型，捕捉学生时间序列中每一时间步长下学生行为之间短期的依赖关系以及相邻学习周期之间长期的模式和趋势；最后通过基于代价敏感性学习的均方误差分离算法训练预测模型，解决数据集中类别不平衡问题。实验结果表明，所提DPSDL 策略可以有效提升在不同学习周期对辍学高风险学生的预测准确性，从而为教学者及时干预学生、提升MOOC教学质量提供合理的建议。