基于Backstepping 的多矢量推力平流层飞艇控制方法研究
2023-02-27张恒杨慧王宇
张恒,杨慧,王宇
(201620 上海市 上海工程技术大学 航空运输学院)
0 引言
临近空间指的是距离地面20~100 km 的空间区域,该区域包含了大气平流层、中间层以及电离层的一部分区域,这一区域正好位于传统飞行器的最高飞行高度和航天器的最低轨道高度之间。近些年来,该空间区域的平流层成为连接航空和航天的一个新的空间领域,在飞行器飞行方面越来越拥有着非凡意义和重要价值[1]。平流层飞艇指的是一种基于浮生气体供给静升力及依靠推进与控制系统完成操纵飞行,且在平流层平均风速较小的高度范围进行长期工作并执行特定任务的浮空类飞行器。本文将介绍一种多矢量推力平流层飞艇,目前已普遍应用在卫星探测、应急救灾、区域导航、安全侦查等领域。在性能方面,平流层飞艇具有无可比拟的优越性:(1)可承载质量较大;(2)在空间停留工作时间长;(3)具有一定的隐身性能;(4)在平流层空间的生存能力强。拥有诸多性能的平流层飞艇在效费比方面自然有着较高的优越性,目前已经成为航天航空领域的重点研究对象。
多矢量推力平流层飞艇在飞行及其工作过程中易受到各种外部干扰的影响,比如平流层中空气湿度变化、风力干扰等情况,这些外界干扰往往会使飞艇机体出现晃动,甚至导致飞艇的运动轨迹偏离既定的路线,因此通过各种控制方法设计出抗干扰能力强的鲁棒飞行控制系统是十分有必要的[2]。
反演(Backstepping)设计方法,通常又被称为后退法、回推法或反步法,主要是针对一种不确定性系统。Backstepping 设计的基本思想是:将一个复杂的非线性多阶系统分解成多个一阶子系统(不超过原系统阶数),再为每个1 阶子系统分别设计Lyapunov 函数以及中间虚拟控制量,通过构造Lyapunov 函数设计控制器,一步一步设计满足要求的虚拟控制,从而设计出真正的控制律[3]。Backstepping 控制方法一般结合Lyapunov 型自适应律使用,将控制律以及自适应律作为一个整体考虑,让整个闭环系统满足预想中的动静态性能指标[4]。
本文重点研究飞艇轨迹跟踪,将Backstepping控制理论应用到多矢量推力平流层飞艇控制中。当飞艇沿着既定的轨迹运动时,该控制方法会迫使飞艇跟随给定点。在多矢量推力飞艇运动学和动力学的基础上,推导出多矢量推力平流层飞艇的非线性控制律,即使在风扰动下也能跟踪既定位置。仿真证实了所提出的Backstepping 控制算法能够稳定整个系统,并驱动飞艇达到期望的位置和偏航角轨迹。
1 多矢量推力平流层飞艇空间运动模型
在oxyz 坐标系下,利用牛顿定律,对飞艇受作用于振中的力和力矩,得到其动力学方程:
式中:M——飞艇质量矩阵;(xG,yG,zG)——飞艇重心位置;m——飞艇质量;mii(i=1,2,…,6)——平流层飞艇的附加质量;Ix,Iy,Iz——飞艇的3 个惯性矩;——平流层飞艇的3 个线加速度;——绕艇体的3 个角加速度。平流层飞艇所受外力和力矩分别为气动力FA、重力和浮力FGB、科氏力FI和矢量推力FT。
根据飞艇的动力学和运动学模型可知[5-6],平流层飞艇的气动力为
式中:q∞——气流的动态压力;Cx——水平力气动系数;Cz——垂直力的气动系数;Cmy——主俯仰力矩的气动系数;Sref=Vol2/3——参考区域;Lref=Vol1/3——参考长度;Vol——飞艇的体积。
飞艇所受重力和浮力的矢量和为
式中:θ,ψ,φ——飞艇的俯仰角、偏航角、滚转角;x,y,z——飞艇的位置坐标。
设控制输入uinput=[fxfyfzmxmymz]T,动力学方程(1)、运动学方程(8)、(9)可根据以下状态向量将其改写为状态空间形式:
飞艇的结构示意图如图1 所示。

图1 飞艇结构示意图Fig.1 Structure diagram of an airship
2 基于Backstepping 的控制器设计及稳定性分析
通过Backstepping 控制方法,可以使得系统(1)遵循所需轨迹的控制律。为此我们通过以下步骤构造控制律:
定义跟踪误差:
因此,通过Lyapunov 稳定性理论,控制律式(20)使得上述跟踪误差渐近收敛至0。所以,通过式(11)—式(20),整个系统(10)对于控制律是渐近稳定的:
3 仿真结果
为了验证所提出的基于Backstepping 控制得到的控制律的有效性,采用变步长Rung-Kutta 方法对多矢量推力平流层飞艇进行了仿真。飞艇主要参数如表1 所示[8]。

表1 平流层飞艇模型参数Tab.1 Parameters of stratospheric airship model
针对基于Backstepping 设计的控制器,设定控制参数c1=5eye(6)和c2=eye(6);初始条件为x1=[0 0 0 0 0 0]T和uinput=[0 0 0 0 0 0]T;参考轨迹为。
图2—图5 分别给出了多矢量推力平流层飞艇的位置和跟踪误差。图2 和图3 中,位置x,y,z 和偏航角均可快速收敛(约2 s),并可以保持预期的轨迹。位置和偏航误差指数都收敛于零,这是由于当跟踪误差开始变大时,反馈控制能够保证系统状态高速收敛到期望值,由此可见平流层飞艇能够快速地沿着预期的轨迹飞行。此外,由图4 可见,倾斜角度(俯仰角和滚转角)优化,从而使用最小的能量。对于控制输入信号,如控制输入和偏转角μ1,μ2,μ3,μ4,均可有效跟踪所需轨迹,并能够迅速趋于稳定。最后,外部推进器可以提供等量的力,垂直向上,以平衡浮力(如图6 和图7 所示),这在物理学上是可以实现的。

图2 x,y 位置跟踪信号图Fig.2 Position tracking signal diagram of x and y

图3 位置z 和偏航角ψ 跟踪信号图Fig.3 Position tracking signal diagram of z and yaw angleψ

图4 滚转角φ 和俯仰角θ 跟踪信号图Fig.4 Position tracking signal diagram of roll angleφ and pitch angleθ

图5 x,y,z 和ψ 的跟踪误差Fig.5 The tracking error of x,y,z andψ
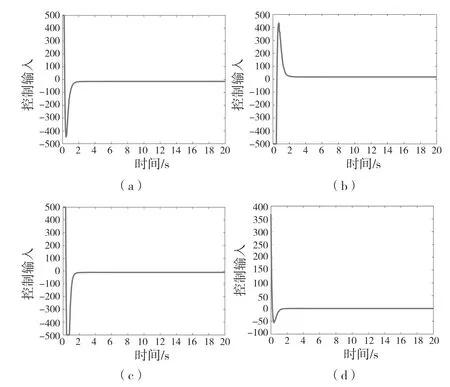
图6 4 个矢量推进器的控制输入Fig.6 Control inputs for four vector thrusters

图7 4 个矢量推进器的偏转角度Fig.7 The deflection Angle of the four vector thrusters
4 结论
本文介绍了一种多矢量推力平流层飞艇动力学建模,基于Backstepping 理论推导出多矢量推力平流层飞艇非线性控制律,该控制律能够使得文中所述系统具有Lyapunov 稳定性;利用MATLAB软件进行了仿真分析。仿真结果显示,所提出的Backstepping 控制算法能够稳定整个系统,并将飞艇驱动到所要求的位置和偏航角的轨迹上。此外,对比非线性系统的Backstepping 控制与传统控制方法,Backstepping 控制在抗风扰能力、克服非线性的干扰、工程实现方面取得了较大的进步,很大程度上提高了平流层飞艇的飞行控制的鲁棒性和精确性。
