网联环境下混合动力汽车分层能量管理策略
2023-02-27张鹏飞于天齐
张 扬,梁 栋,张鹏飞,于天齐,张 乔,胡 博
(重庆理工大学 车辆工程学院,重庆 400054)
0 引言
交通拥堵中的汽车因频繁启停造成的油耗、排放增加问题日渐受到关注。为避免红灯停车和跟车启停,用于实现车与车(vehicle to vehicle,V2V)、车与路(vehicle to infrastructure,V2I)间信息通信的智能网联技术孕育而生[1-3]。混合动力汽车(hybrid electric vehicle,HEV)因其油耗低、续航长、能量可回收等优点已受到企业强烈关注[4]。智能网联和能量管理策略的结合运用是实现HEV油耗、排放最小化的重要途径[5-6]。Chen等[7]提出一种提升燃油经济性的预测巡航控制方法,通过控制发动机扭矩、制动力矩和挡位切换优化车速,将燃油效率提升了8%。Homchaudhuri等[8]针对城市道路工况的智能网联车队提出一种分层控制框架,上层控制器基于MPC优化车速,下层控制器利用自适应的等效燃油最小策略(equivalent consumption minimization strategy,ECMS)算法对并联式HEV进行能量管理,提升车队整体的燃油经济性,减少CO2排放。Du等[9]在网联环境下对车队通过信号灯路口的能量管理进行研究,并考虑了车辆换道决策的过程,实现了网联车辆的变道,提升了燃油经济性。Mahler等[10]考虑信号灯相位变化,通过历史和实时数据预测信号灯状态,利用最优控制得出零启停和最佳油耗的速度轨迹。钱立军等[11]运用分层控制策略降低四驱混合动力汽车的油耗,并利用硬件在环验证了策略的有效性。邱利宏等[12]提出了考虑效率反馈的双层控制系统,提高了车队整体的燃油经济性。上述研究均考虑单车场景或车队场景下的燃油经济性提升,未考虑车辆行驶过程中偶遇前车的情况。
本文以串联式混合动力汽车为研究对象,在城镇道路背景下,设计了分层式模型预测控制(MPC)算法优化车辆行驶车速与燃油消耗,并对偶遇前车的情况进行仿真。首先,建立车辆纵向动力学模型,以此设计上层MPC控制策略得到最优目标车速。其次,建立串联式混合动力系统模型,根据最优车速计算的需求功率,设计下层MPC能量管理控制策略,控制动力系统的输出功率分配。将仿真结果与DP的结果进行对比,以验证分层式MPC策略的性能。
1 网联环境下的分层控制原理
网联环境下可通过V2V和V2I通信技术实现车辆状态信息的传输共享,原理如图1所示[13]。

图1 车联网原理示意图
在网联环境下,一般采用分层控制优化车辆的燃油经济性。上层利用信号灯正时(signal phase and timing,SPAT)与前车信息求解最优目标车速,下层根据目标车速优化燃油经济性。本文利用分层式模型预测控制对单车控制的燃油经济性进行优化,上层控制系统基于MPC求解最优目标车速,下层控制系统基于MPC,利用上层系统求解的目标车速提升燃油经济性,分层模型预测控制原理如图2所示。

图2 分层模型预测控制原理示意图
2 上层速度优化
以串联式混合动力汽车为研究对象,其动力系统模型如图3所示,系统参数如表1所示。

图3 串联式HEV结构示意图

表1 混合动力汽车参数
2.1 车辆动力学模型与油耗模型
由于只根据V2V、V2I信息进行速度优化,故忽略考虑横向、垂向控制,建立车辆动力学模型[14]:
(1)
式中:v(t)为车辆t时刻的速度;s(t)为车辆t时刻的位置;u(t)为车辆t时刻的加速度;M为整车质量;Cd为风阻系数;ρ为空气密度;Af为车辆迎风面积;f滚阻系数。
在上层车速优化中,为实现良好的燃油经济性需要合适的车辆油耗模型,由于只根据SPAT、前车等信息进行优化,未考虑传动系统内部情况,无法通过发动机转速、转矩计算油耗。因此把汽车行驶单位距离的功率消耗作为近似油耗模型,如式(5)所示[15]。
β(v(t)Mu)+(1-β)(-ηrec(t)Muv(t))
(2)
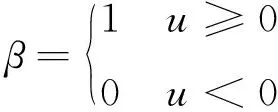
(3)
(4)
(5)
式中:Pw(t)表示车辆行驶时消耗的功率;ηrec为控制器的调整效率;ηeff表示能量转化效率;HLHV为燃油的低热值;maverage表示车辆行驶单位距离的能量消耗。
2.2 车速规划方程
根据信号灯信息得到车辆能够在绿灯时间内通过路口的车速范围以作为车速状态量的约束。然后在该车速范围内选择合适的车速值作为MPC目标车速。为提高道路通行效率,减少固定行程总时间,将速度规划方程得出的车速范围上限值作为被控车辆的目标车速。目标车速范围规划原理如图4所示,计算方程如下[8]:

图4 目标车速规划原理示意图

(6)
vtarget(t)=vub(t)
(7)

(8)
tcycle=tr+tg
(9)
(10)
式中:vtarget(t) 为被控车辆的目标车速;vmax为道路限速;da(t)是被控车辆距前方交通信号灯a的距离;t是车辆行驶的总时间;tr是红灯状态剩余持续时间;tg是绿灯状态剩余持续时间;tcycle为信号灯的循环周期;Kw为信号灯状态循环次数;函数mod()产生t除以tcycle的余数。在建模过程中,设置的信号灯以红灯开始,且当t=Kwtcycle时,Kw加1以计算信号灯循环次数。
为避免被控车辆红灯停车,必定存在某个速度下限,使得车辆在绿灯结束前通过路口。计算公式如(11)所示。结合式(6)得到目标车速范围[vlb(k),vub(k)]。其中,vub为车速上限,vlb为车速下限。当且仅当车速保持在目标车速范围内,车辆才能避免红灯停车。
(11)
2.3 最优速度求解
本节设计的MPC目标函数中包含4个子目标,分别为:J1(t)表示燃油消耗;J2(t)表示控制车辆与前车的相对距离与安全跟车距离的差值;J3(t)表示目标速度跟随的误差;J4(t)表示加减速次数,目标函数形式如下[15]:

w3J3(t)+w4J4(t)]
(12)
(13)
J2(t)=[S0+th(v(t)-vp(t))+
(sh(t)-sp(t))]2
(14)
J3(t)=(v(t)-vtargret(t))2
(15)
J4(t)=u(t)2
(16)

(17)
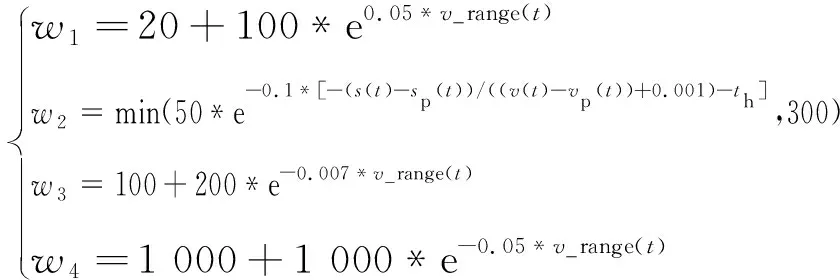
(18)
式中:S0为理想跟车距离;v为被控车辆速度;vtargret为目标速度;vp为前车速度,vub与vlb为目标车速的上、下限;u为被控车辆加速度;umax、umin分别为加速度上下限;sp为前车位置;v_range表示目标车速范围的大小;w1,w2,w3,w4为权重系数,w1为燃油消耗权重,优化燃油经济性;w2与跟车距离(s(t)-sp(t))和相对速度(v(t)-vp(t))有关,以调整车辆跟车距离;w3为速度跟随误差权重,使优化的速度尽可能接近目标车速,减少车辆红灯停车次数;w4为控制量权重以减少加减速次数、加速度绝对值的大小,提高乘坐舒适性。目标函数中的2个约束为车速约束、加速度约束。
由于MPC目标函数非线性,采用序列二次规划优化算法,根据当前红绿灯正时信息、前车与被控车辆的车速、位置等信息,结合MPC优化得到的加速度、整车动力学模型计算出被控车辆的最优速度和位置轨迹。
3 下层能量管理
HEV行驶时总的需求功率由发动机和电池的输出功率共同满足,能量管理是根据需求功率以高效方法合理安排发动机和电池的功率输出以提高燃油经济性。
3.1 需求功率的确定
考虑水平直线行驶的HEV,其动力系统产生的总能量最终转换为滚动阻力耗散能Proll、空气阻力耗散能Paero以及加速所需能量Pacc,根据能量守恒定律,计算HEV行驶总需求功率Pdmd:
Pdmd=Pacc+Proll+Paero=
(19)
式中:ηm为机械传递效率;Cd为空气阻力系数;Af为迎风面积;v为目标车速;ρ为空气密度。
3.2 建立MPC预测模型
预测模型是应用模型预测控制算法的基础,可根据被控对象的系统模型建立。为避免预测模型过于复杂而降低控制系统实时性,根据电池SOC慢动态过程,简化系统模型。以电池SOC作为状态变量,发电机转矩和发动机转速作为控制变量,预测的需求功率作为干扰量建立状态空间方程作为MPC的预测模型。忽略发动机和电机的转动惯量,预测模型如下[16]:

(20)
y=g(x,u)
(21)
式中:x=SOC为状态变量;u=[Tg,ne]T为控制变量;v=Pdmd为可测量干扰量;y=Pout为输出变量。
对式(20)、(21)线性化与离散化,得到线性时变的动力系统模型:

(22)

(23)
3.3 目标函数与最优控制量求解
考虑发动机发电机组的输出功率尽量满足需求功率,同时电池SOC维持在合理的范围,设定目标函数如下:
β3(x(k+N-1)-xref)2
(24)

(25)

4 仿真与分析
通过Matlab/Simulink仿真平台分别对单车与双车场景控制策略的有效性进行仿真分析,以验证所提出的分层式模型预测控制算法的性能。依据文献[17]提供实际行驶场景,设置26个信号灯路口,其中红灯绿灯的持续时间均为60 s。被控车辆从起点出发,道路限速为60 km/h,最低限速为0 km/h,道路能提供的最大驱动加速度为2 m/s2,减速制动-2 m/s2。
4.1 单车行驶场景
仿真得到网联环境下单车行驶轨迹,如图5所示。其中,水平虚线的红色部分表示红灯时间窗口,空白部分则表示绿灯时间窗口,黑色实线表示被控车辆的行驶轨迹,绿色实线是作为对比的以60 km/h匀速行驶的车辆行驶轨迹,仿真共运行1 600 s,车辆行驶了16 km,共通过26个交通灯路口。

图5 单车行驶轨迹曲线
车辆行驶过程中,黑色轨迹线与虚线红色部分均未交叉,证明车辆总是绿灯状态时通过路口,没有违反交规,且多数情况是红灯状态结束,绿灯状态开始时通过路口;绿色轨迹线在抵达红灯路口时会停车等待,且抵达终点时的总时长高于黑色轨迹线说明基于MPC的上层目标车速优化方法可以减少被控车辆红灯停车次数、发动机怠速空转时间、降低油耗、提高道路通行效率。
车辆速度曲线如图6—7。图6为网联环境下基于MPC速度优化的车辆速度曲线,其中,红色实线为速度曲线,黑色虚线为速度规划方程计算的车速上限,紫色虚线为车速下限。可以看出:在单车场景中,被控车辆行驶速度始终保持在车速上下限范围内。在抵达终点以前,车速始终大于零,且未超过限速,说明被控车辆在行驶过程中,既未停车也没有违反交规。图7为匀速行驶的车辆速度曲线。
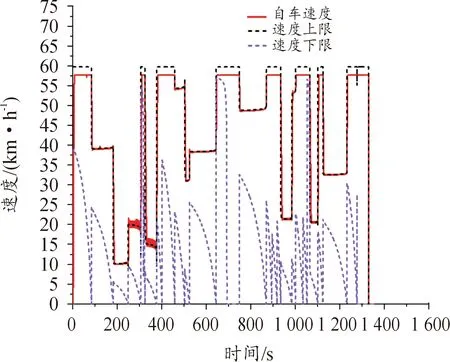
图6 基于MPC的单车速度曲线
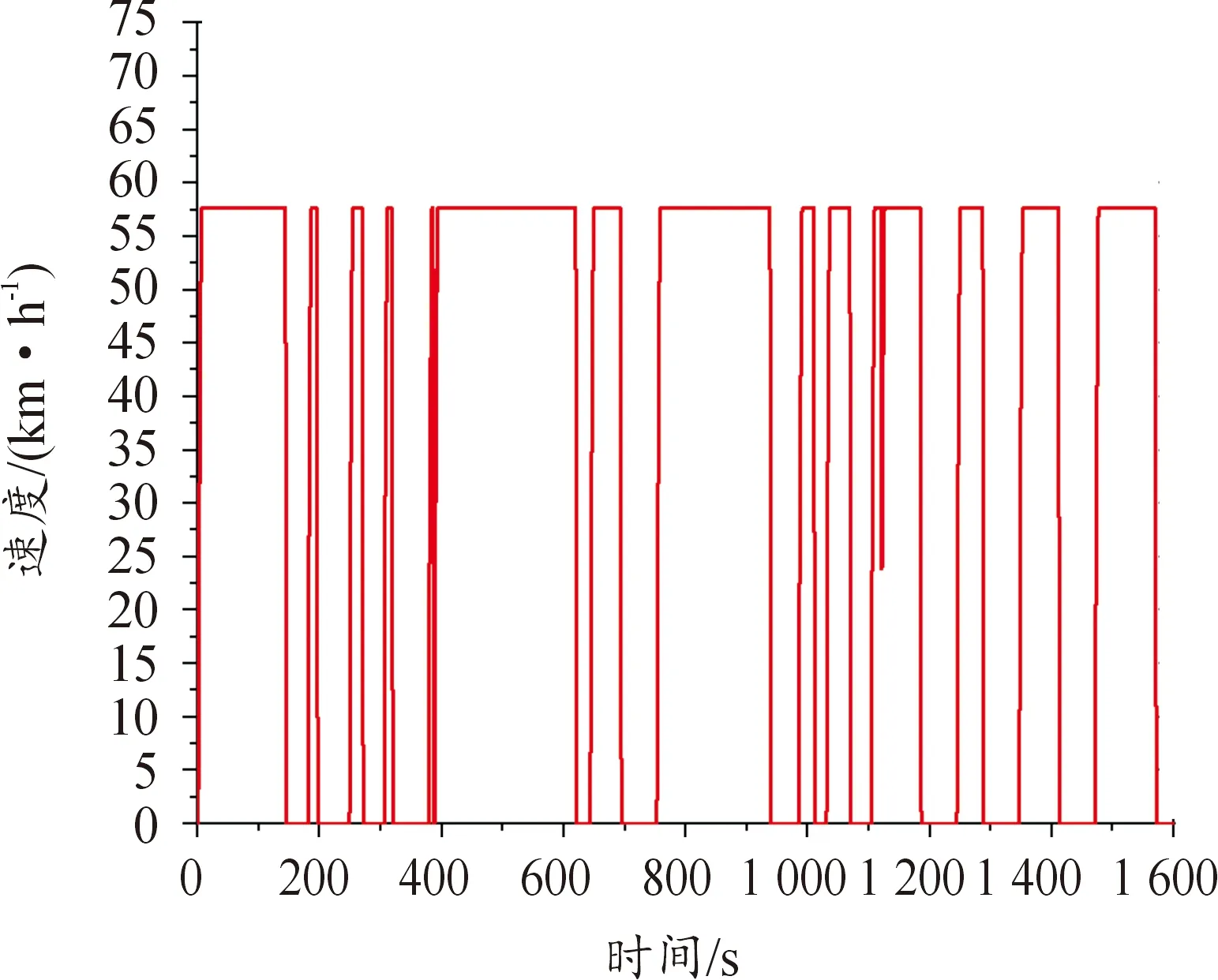
图7 匀速行驶单车速度曲线
4.2 双车行驶场景
在双车场景中,被控车辆前方会出现其他车辆,双车行驶轨迹如图8所示。其中,黑色实线与蓝色实线分别表示前车与自车的位移,绿色实线为匀速行驶的车辆行驶轨迹,作为蓝色实线轨迹的对比,当匀速行驶的车辆跟车距离达到安全跟车距离时,以前车的速度作为目标车速行驶。图中两车轨迹没有重叠或交叉,说明被控车辆跟车时,间距始终大于零,没有发生超车、撞车的情况。车辆在行驶到第5、6位置的信号灯时,由于两信号灯的间隔较近,前车通过路口以后,被控车辆无法在当前绿灯时间窗口通过,所以提前进行了减速,在下一个绿灯通过路口。仿真完成时,前后车均已抵达终点,匀速行驶的车辆行驶到第25个信号灯附近,比进行速度优化的车辆需要更长的行驶时间。

图8 双车行驶轨迹曲线
被控车辆速度曲线如图9。同样,红色实线为被控车辆的速度曲线,黑色虚线为目标车速上限,紫色虚线为车速下限。可以看出:被控车辆的行驶速度始终保持在车速上下限内。在抵达终点以前,被控车辆的车速始终大于零,且未出现超过限速的情况,说明被控车辆在行驶过程中,既未停车也没有违反交规,验证了基于MPC的上层速度优化系统性能良好。

图9 基于MPC的速度曲线
4.3 下层能量管理结果
在Simulink模型中设定的SOC参考值为0.7,整车质量为1 480 kg,电池容量为200 Ah,预测步长为0.1 s。仿真结果如图10—16所示。

图10 匀速行驶车辆的速度曲线
由图11可知,实际车速与目标车速的跟踪情况良好,可以看到基于MPC的下层能量管理控制系统可以保证车辆的动力性,满足车辆行驶的功率需求。图12为电池SOC的变化过程,经历了1 570 s的仿真后,电池SOC从初始值0.7降到了0.698,最大下降幅度为0.035,可以认为本文提出的基于MPC的能量管理策略可以很好地管理电池SOC。

图11 速度跟踪曲线
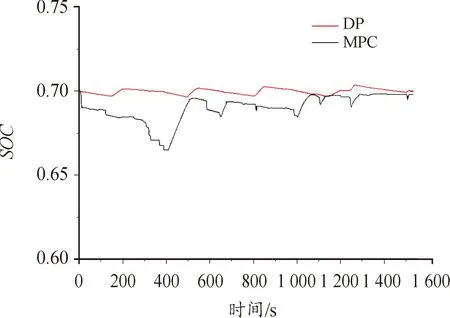
图12 电池SOC状态
图13—图15分别为驱动电机转速、发动机转速与发电机转矩曲线,可以看到电机转速明显受到目标车速的影响,且电机转速的波动适应车速的变化,而发动机发电机组的转速与车速已经解耦,在车速改变的同时,其转速的变化没有明显的波动。

图13 驱动电机转速曲线

图14 发动机转速曲线

图15 发电机转矩曲线
图16为发动机工作点分布图,可以看到发动机的实际工作点大部分都处于发动机高效率区域。

图16 发动机工作点示意图
为了验证基于MPC能量管理策略的经济性,与相同工况下基于动态规划的能量管理策略进行了结果对比分析。基于动态规划的HEV能量管理目标是求解全局最优的车辆控制序列,在维持SOC的同时达到油耗最低,其结果如图12与表2所示。动态规划的电池SOC变化如图12中的红色曲线所示,表2为2种能量管理策略对应的油耗值,以及整个工况最后的终端SOC值。

表2 不同策略油耗值和电池终端SOC
采用的基于MPC能量管理的控制策略,与基于动态规划能量管理的控制策略相比,油耗只高出6.7%。在电量维持方面,基于MPC的控制策略与动态规划控制策略在终端时刻的SOC只有0.002的差距,根据对比结果可以看出本文采用的基于MPC的下层能量管理系统的性能良好。
5 结论
为减少车辆红灯停车次数、提升燃油经济性与道路通行效率,利用智能网联技术获得的车辆自身和周围交通环境信息设计了分层式模型预测控制算法。上层控制器根据交通信号灯与车辆行驶状态预测避免红灯停车的最优目标车速,下层控制器依据最优目标车速对串联式混合动力汽车实施能量管理。将仿真结果与动态规划DP的控制策略结果进行对比分析。结果表明:网联环境下,所设计的上层MPC速度优化算法可以有效减少车辆红灯停车次数;下层MPC能量管理算法可以有效保持电池SOC,并协调发动机发电机组与动力电池的工作状态,使得发动机工作点尽可能处于高效率工作区域,达到了降低油耗的目的。
