汽车电子节气门的模型参考-扰动观测复合控制

2023-02-27高明，苏忆，赵钱

机械设计与制造 2023年2期

高明，苏忆，赵钱

（1.江苏信息职业技术学院，江苏无锡 214153；2.无锡商业职业技术学院，江苏无锡 214153；3.淮阴工学院，江苏淮阴 223003）

1 引言

节气门作为车辆发动机的“咽喉”，其开度大小通过控制进气量影响汽油与空气的混合比，进而影响燃油的燃烧效率和废气排放。与传统机械节气门相比，电子节气门可以实现更高精度和灵活的进气量控制，达到降低油耗和排放的目的［1］，因此研究电子节气门控制对节能和环保意义重大。

电子节气门虽然结构简单，但是由于机械磨损、摩擦力矩等非线性因素影响和系统参数不确定性影响［2］，传统控制方法难以保证良好的控制效果。电子节气门控制的代表性方法有PID控制、滑模控制、自适应控制、神经网络控制等。文献［3］充分考虑了非线性因素和外界扰动，建立了节气门的数学模型，提出了滑模控制方法，获得了较好的控制效果。文献［4］使用多层感知神经网络辨识和控制非线性电子节气门系统，实现了对设定目标的跟踪控制。文献［5］使用状态观测器估计节气门系统的总扰动，并使用双环积分滑模观测器进行控制，实现了节气门开度和角速度的控制。文献［6］针对电子节气门的非线性特性，设计了改进型积分分离PID控制器，传统PID控制器的超调量小、响应速度快。

以上研究成果都取得了较好的控制效果，但也存在一些缺陷：

（1）神经网络等方法计算量大，难以实现实时控制；

（2）以上研究大都只考虑非线性因素影响，而没有考虑系统参数不确定性的影响。

这里以电子节气门的精确控制为目标，设计了模型参考自适应控制器，使用扰动观测器对外界扰动和参数不确定性进行实时估计，将模型参考自适应控制器与扰动观测器结合，设计了复合控制器，实现了在扰动和参数不确定性情况下的精确跟踪，提高了系统鲁棒性。

2 电子节气门控制系统原理及模型

2.1 电子节气门控制系统原理

电子节气门控制系统主要由油门踏板传感器、电控单元、电子节气门组成，油门踏板传感器用于测量踏板深度，反应驾驶员的驾驶意图。电控单元根据车辆参数和驾驶状态，计算并输出节气门控制量。

电子节气门本体主要由直流电机、齿轮组、复位弹簧和位置传感器组成，直流电机通过齿轮组带动节气门阀片转动；复位弹簧作用是在无电状态下使节气门复位，同时起到转动阻尼的作用；位置传感器作用为测量节气门实际开度。节气门控制系统的原理方框图，如图1所示。

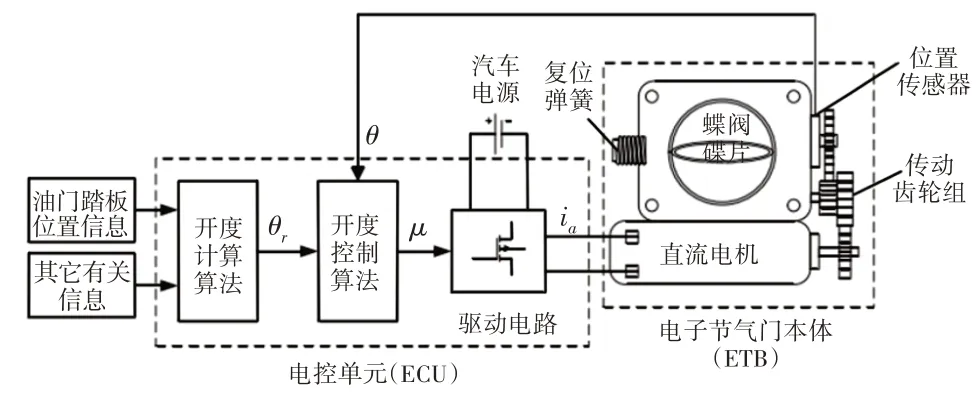
图1 电子节气门控制系统Fig.1 Control System of Electronic Throttle

电子节气门控制包括开度计算和开度控制两个方面，开度计算是指根据当前的驾驶员意图和驾驶模式、发动机转速等车辆状态，计算节气门的最佳开度θr，达到降低能耗和排放的目的。开度控制是指根据最佳开度θr和传感器测量的实际开度θ，通过算法依据开度误差设计控制律μ，实现节气门对最佳开度的高精度跟踪。这里研究内容为电子节气门的开度控制方法，对开度计算方法不做研究。

2.2 电子节气门模型

本节对电子节气门的关键部件进行建模，根据部件的连接关系得到其原理方框图。

（1）直流电机。直流电机的等效原理图，如图2所示。图中：Vm—电机的输入电压；L—直流电机的电枢电感；R—电机内阻；Em—电机转动的反电动势；i—电机内电流。

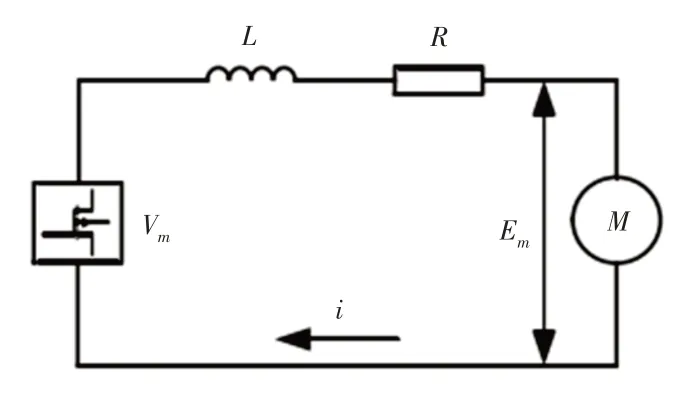
图2 直流电机模型Fig.2 Model of DC Motor

直流电机中电枢的电感值极小，一般忽略不计，因此得到电机内电流和电机输出转矩Tm为［7］：

式中：km—反电动势系数和转矩系数；ωm—转子角速度。

根据定轴转动定律和转矩平衡方程，得到直流电机动力方程为：

式中：Jm—转子的转动惯量；TL—负载转矩。

（2）H桥驱动模块。H桥驱动模块用于控制电机输入电压Vm的大小和方向，工作原理图，如图3所示。

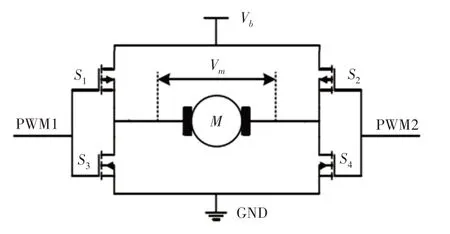
图3 H桥驱动模块Fig.3 Driver Module of H-Bridge

PWM1 和PWM2 通过控制场效应管S1、S2、S3、S4的通断来控制电流方向，当S1、S4导通而S2、S3截止时，电流由Vb经S1、电机、S4到达接地端，此时电机正转；当S2、S3导通而S1、S4截止时，电流由Vb经S2、电机、S3到达接地端，此时电机反转。电机的输入电压Vm与PWM占空比有关［8］，即：

式中：μ(t)—与PWM占空比相关的比例系数。

（3）复位弹簧模型。这里以柴油机电子节气门为研究对象，阀片在掉电状态下（即静态位置）为全开状态，由一根复位弹簧控制完成。复位弹簧在静态位置处为非自然拉伸状态，存在初始力矩T0。另外为了建模方便，将阀片在静态位置的角度定义为0°，因此复位弹簧的力矩模型为：

式中：Ts—弹簧的复位力矩；ks—弹簧的劲度系数；θ—阀片的开度；T0—弹簧在静态位置的初始力矩。

（4）传动齿轮组模型。电机的转动力矩通过齿轮组作用到节气门阀片转轴，齿轮组使用转动惯量小的轻质塑料制作而成，因此其对系统的影响可忽略。记齿轮传动比为n，则电机负载转矩TL与阀片转轴转矩Tg、电机转子转角θm与阀片转角θ的关系为：

（5）摩擦力矩模型。电子节气门控制过程中的摩擦力矩包括两个方面：一是齿轮传动的摩擦，二是阀片转动的摩擦。由于油污积碳、部件老化等原因，很难建立阀片转动的摩擦力矩模型，因此这里将摩擦力矩视为扰动力矩，通过设计状态观测器和自适应控制器对其进行控制。

（6）电子节气门数学模型。以电子节气门阀片转轴为对象，其力矩平衡方程为：

式中：Jg—阀片转轴的转动惯量；Tf—摩擦力矩；Ta—气流冲击力矩。将式（1）～式（5）代入式（6），可得：

令J=n2Jm+Jg，d0=T0+Tf+Ta，ω=，则电子节气门数学模型可以简化为：

2.3 设定控制目标

电子节气门控制目标设定为：

（1）误差带为±5%时，阶跃信号跟踪的调节时间≤250ms；

（2）稳态误差≤1%；

（3）超调量≤1%；

（4）控制策略对硬件要求不高，防止使用成本过高的控制器。

3 模型参考自适应控制器

本节忽略摩擦力矩、部件老化、系统参数不确定性等因素影响，设计了模型自适应控制器。在第4节中设计扰动观测器用于消除摩擦力矩、部件老化等干扰因素的影响。

3.1 模型参考自适应控制原理

模型参考自适应控制的前提是被控对象模型和控制性能指标已知。根据性能指标可以设计一个参考模型，此参考模型具有期望的闭环系统性能。在输入作用下，根据参考模型和被控对象的输出误差设计反馈控制律，使被控对象与参考模型具有相同输出，则被控对象具有与参考模型相同的系统性能。当被控对象参数未知或存在不确定性时，需要使用自适应律实时修正未知参数。模型参考自适应控制的原理［9］，如图4所示。

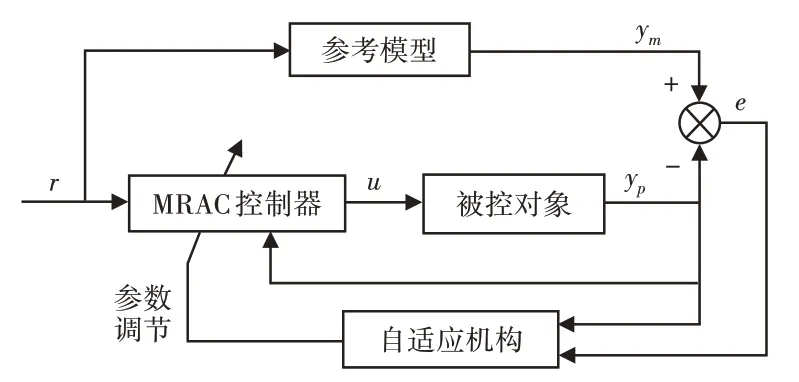
图4 模型参考自适应控制Fig.4 Model-Reference Adaptive Control

在模型参考自适应控制中，参考模型决定了系统的动态性能和稳态性能，控制器用于产生被控对象的控制量，控制器的参数是时变的，由自适应机构实时确定。模型参考自适应控制的设计方法有局部参数最优化设计法和Lyapunov稳定性设计法，前者设计后需进行稳定性判断，较为复杂，这里选用Lyapunov稳定性设计方法。

3.2 控制系统设计

模型参考自适应控制分为确定参考模型、设计控制律、设计参数的自适应律等3个步骤。

3.2.1 确定参考模型。

参考模型决定了控制系统的动态系统和稳态性能，若参考模型性能过高，则执行机构的反应速度跟不上，达不到控制效果。若参考模型性能过低，则无法体现控制的目的。参考电子节气门的数学模型，这里选择典型的二阶系统作为参考模型，为：

式中：ξ—系统的阻尼系数；ωn—无阻尼角频率。

为了达到2.3节设定的节气门控制目标，兼顾控制的快速性和精确性，将特征参数取值为ξ=1、ωn=25。参考模型的阶跃响应，如图5所示。

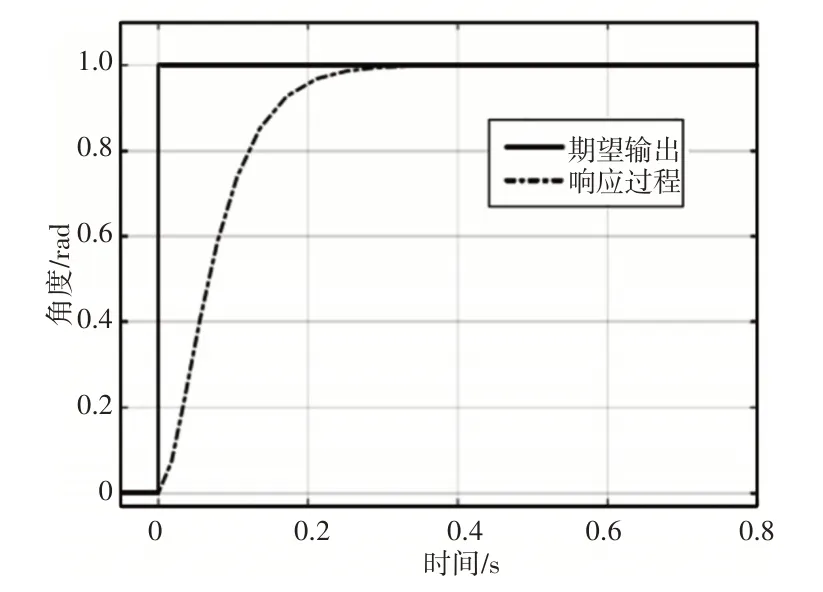
图5 参考模型的阶跃响应Fig.5 Step Response of Reference Model

结合图5和模型参数，参考模型的超调量为0，稳态误差为0，到达误差带的调节时间为210ms，3项性能指标均满足设定目标。选择状态量xm1=θm、xm2=，则参考模型状态方程为：

3.2.2 控制律设计

依据式（8），令bp=选择电子节气门状态量为x1=θ、x2=，将式（8）转化为状态方程为：

将式（10）与式（11）相减，得：

系统进入稳态过程后，稳态跟踪误差为0，则式（12）左端为0，由此得控制律μ为如下形式：

式中：k—输入r的前馈增益；f1—电子节气门输出θ的反馈增益；f2—的反馈增益。通过自适应调整参数k、f1、f2可以实现电子节气门对参考模型的完全跟踪。

3.2.3 参数的自适应律设计

定义参数误差向量ϕ和跟踪误差向量e分别为：

则式（14）可以改写为矩阵形式，即：

根据Lyapunov 稳定法［10］设计参数的自适应律，Lyapunov 函数设计为：

式中：P=—对称正定矩阵，元素值在推导过程中给出；Γ=diag(λ1，λ2，λ3) —正定对角矩阵，表示自适应律的系数矩阵。由此可知V>0。

将Lyapunov函数求导，得：

为了使≤0，即保证系统具有Lyapunov稳定性，令上式后3项为0，且PA+ATP=-2I，则矩阵P的元素值可由此确定。另外，有：

电子节气门参数ap1、ap2、bp是关于时间的缓变函数，模型参数am1、am2、bm是一个常值，因此有则式（17）可转化为：

由此得参数的自适应律为：

按照式（18）的参数自适应律进行控制，不仅能够保证系统的稳定性，而且能够满足控制的动态和静态性能要求。

4 模型参考自适应-扰动观测复合控制

首先设计对干扰和参数不确定性的观测器，而后设计模型参考自适应-扰动观测复合控制器。

4.1 扰动观测器

记参数ap1、ap2、bp的标称值分别为a1、a2、b，参数a1、a2、b的值查阅随产品资料可以获得。记ap1=a1+Δa1、ap2=a2+Δa2、bp=b+Δb，其中Δa1、Δa2、Δb表示参数不确定性。记外界干扰项为d0(t)，参考（11）得：

式中：d(t)=-Δa1x1-Δa2x2+Δbμ-d0(t)—集总扰动，由d(t)表达式可以看出，其中既包含参数不确定性，也包含外界干扰。设计扰动观测器的作用是实时估计d(t)的值，并消除其对控制系统的影响。

选择观测器的状态量为x1=θ、x2=、x3=d(t)。3个状态量的估计值分别记为z1、z2、z3，估计误差分别为：ε1=z1-x1，ε2=z2-x2，ε3=z3-x3。设计线性状态观测器为：

式中：l1、l2、l3—状态观测器的待定系数。

为了简化设计，将特征方程设置为具有3 重特征根-p，则|λI-|=(λ-p)3，由此可得到待定系数为：

至此，扰动观测器设计完毕，其中参数p的大小决定了观测误差收敛到0的速度。

4.2 模型参考自适应-扰动观测复合控制

模型参考自适应-扰动观测的复合控制器，如图6所示。

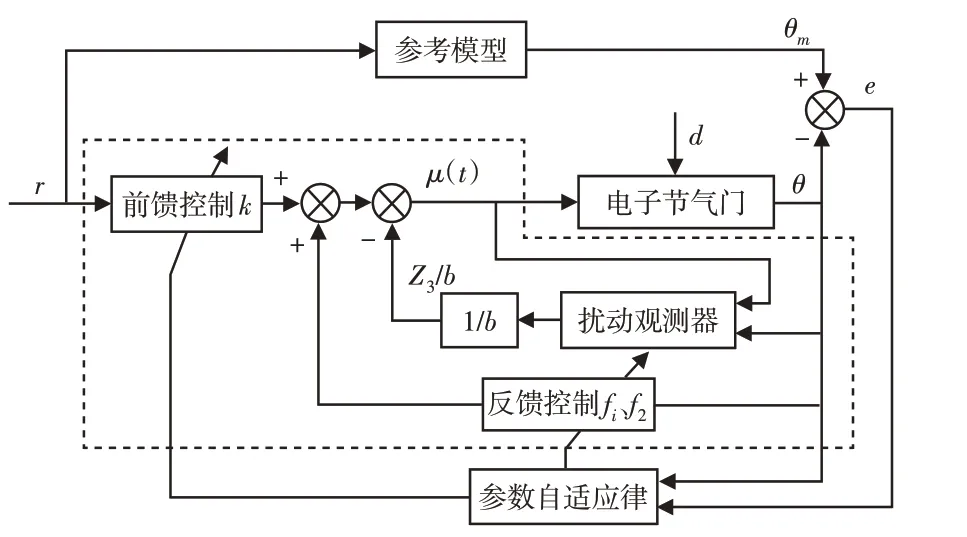
图6 复合控制器Fig.6 Compound Controller

图中虚线框出部分为模型参考自适应-扰动观测复合控制器，复合控制器的控制律为：

复合控制器的Lyapunov 稳定性证明过程较为复杂，在此不再给出其证明过程。经推导，复合控制器具有Lyapunov稳定性。

5 仿真与实验验证

为了验证复合控制器的控制效果，首先在Matlab 软件中进行仿真验证，而后搭建实验平台进行实际控制效果验证。被控电子节气门的标称参数为：电枢电阻R=2Ω，反电动势系数km=0.0217N·m/A，转子转动惯量Jm=3×10-6kg ⋅m2，阀片转动惯量Jg=2×10-6kg ⋅m2，齿轮转动比n=20，弹簧弹性系数ks=0.03Nm/rad，弹簧初始力矩T0=0.18Nm，电源电压Vb=12V。

5.1 仿真验证

在有干扰量和模型失配情况下进行控制效果验证，分别使用模型参考自适应控制器和复合控制器进行控制。干扰量d0(t)在整个过程中设置为0.18N·m，另外在2s时再突然施加一个0.2N·m的干扰力矩。模型失配是指将电子节气门参数R和ks分别增大20%，参数Vb减小20%。

模型参考自适应控制器的参数设置为：自适应律系数λ1=2、λ2=0.25、λ3=2，参数初值f1(0)=-0.2780，f2(0)=-0.0013，k(0)=0.2895。扰动观测器的极点配置p=300。节气门开度的阶跃目标为1rad，模型参考自适应控制器和复合控制器的控制效果，如图7所示。

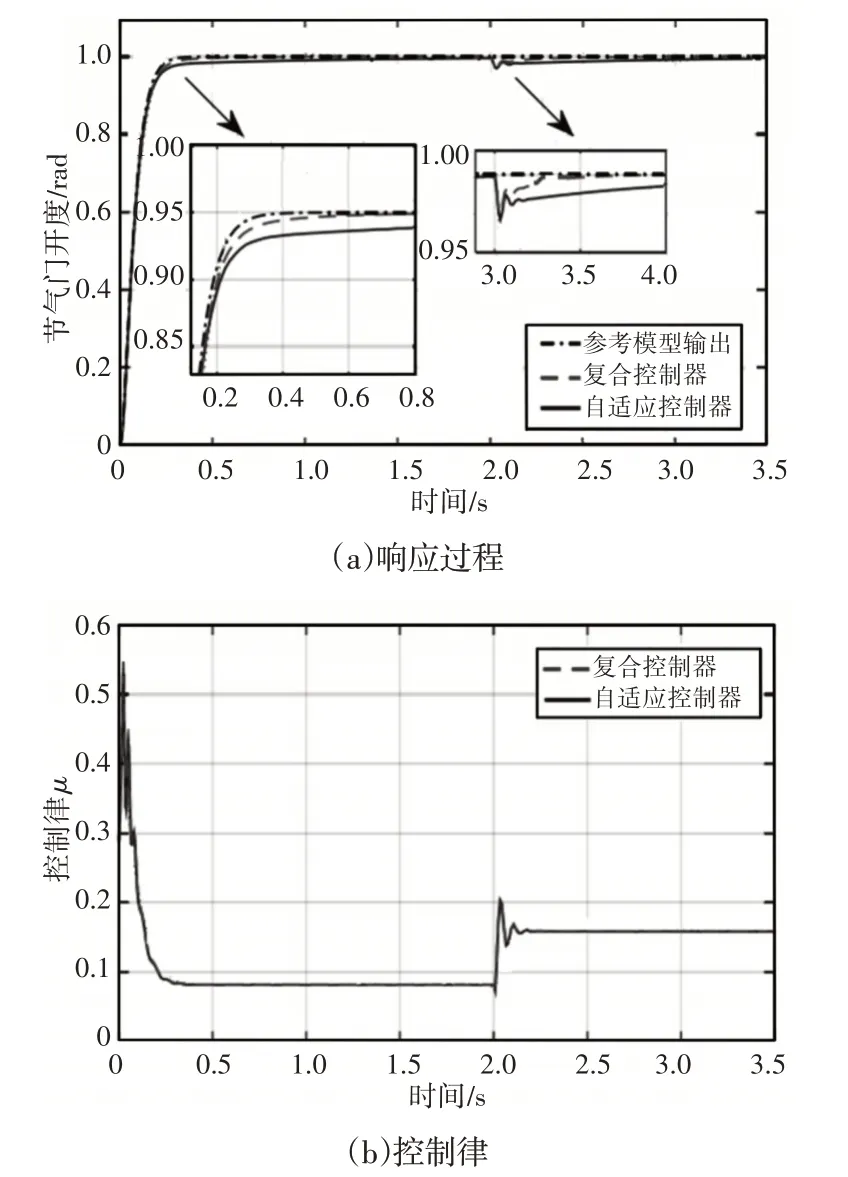
图7 复合控制器与自适应控制器的控制效果Fig.7 Control Effect of Compound Controller and Adaptive Controller

由图7（a）可以看出，由于存在模型失配和干扰问题，模型参考自适应控制器对参考曲线的跟踪存在一定误差，而复合控制器使用扰动观测器实时估计扰动量，实现了对参考模型的快速准确跟踪。在2s突然施加扰动时，复合控制器的跟踪精度受到瞬时影响，但是195ms后再次跟踪期望输出；而自适应控制器的瞬时误差幅度明显大于复合控制器，而且1s后仍未能准确跟踪期望曲线。以上分析说明，复合控制器由于加入了扰动观测器，能够实时估计参数不确定量和外界扰动量，提高了控制精度和系统鲁棒性。

5.2 实验验证

5.1节证明了复合控制器的控制精度和鲁棒性优于模型参考自适应控制器，本节以实验的方法验证复合控制器在电子节气门中的实际控制效果。本节搭建的电子节气门实验平台，如图8所示。主要包括12V直流电源、PWM驱动模块、电子节气门、控制器和上位机软件构成。12V电源为电子节气门提供转动能量，PWM驱动模块模拟H桥驱动模块，用于控制节气门的电压大小和方向，上位机软件可以对dSPACE控制器设置参数，并显示控制结果。

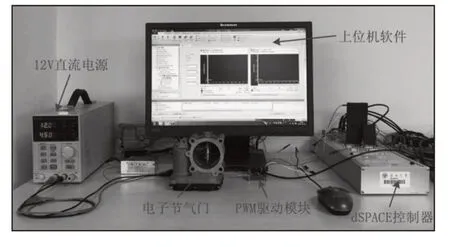
图8 实验平台Fig.8 Experiment Platform

设计两组实验验证复合控制器对电子节气门的实际控制效果。第一组实验是将直流电源电压设置为12V，此时不存在模型失配问题，4s时对电压的控制电压施加-1V的干扰。第二组实验将直流电源电压设置为8V，此时存在模型失配问题，4s时对电压的控制电压施加-1V的干扰。节气门的角度在1s时由10°阶跃至35°，复合控制器在两组实验中的控制结果，如图9、图10所示。

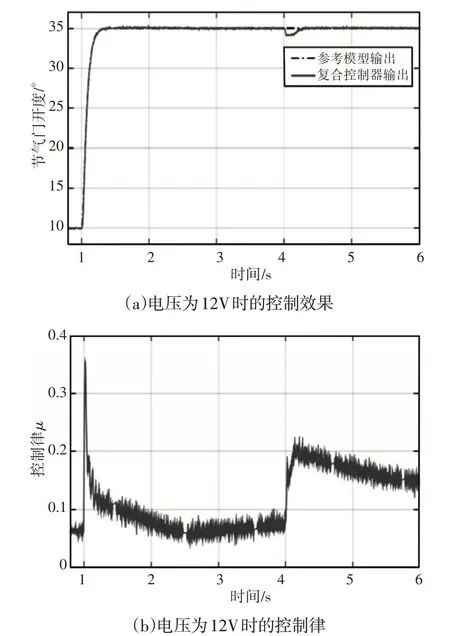
图9 电压为12V时的控制Fig.9 Control Effect when Velocity is 12V

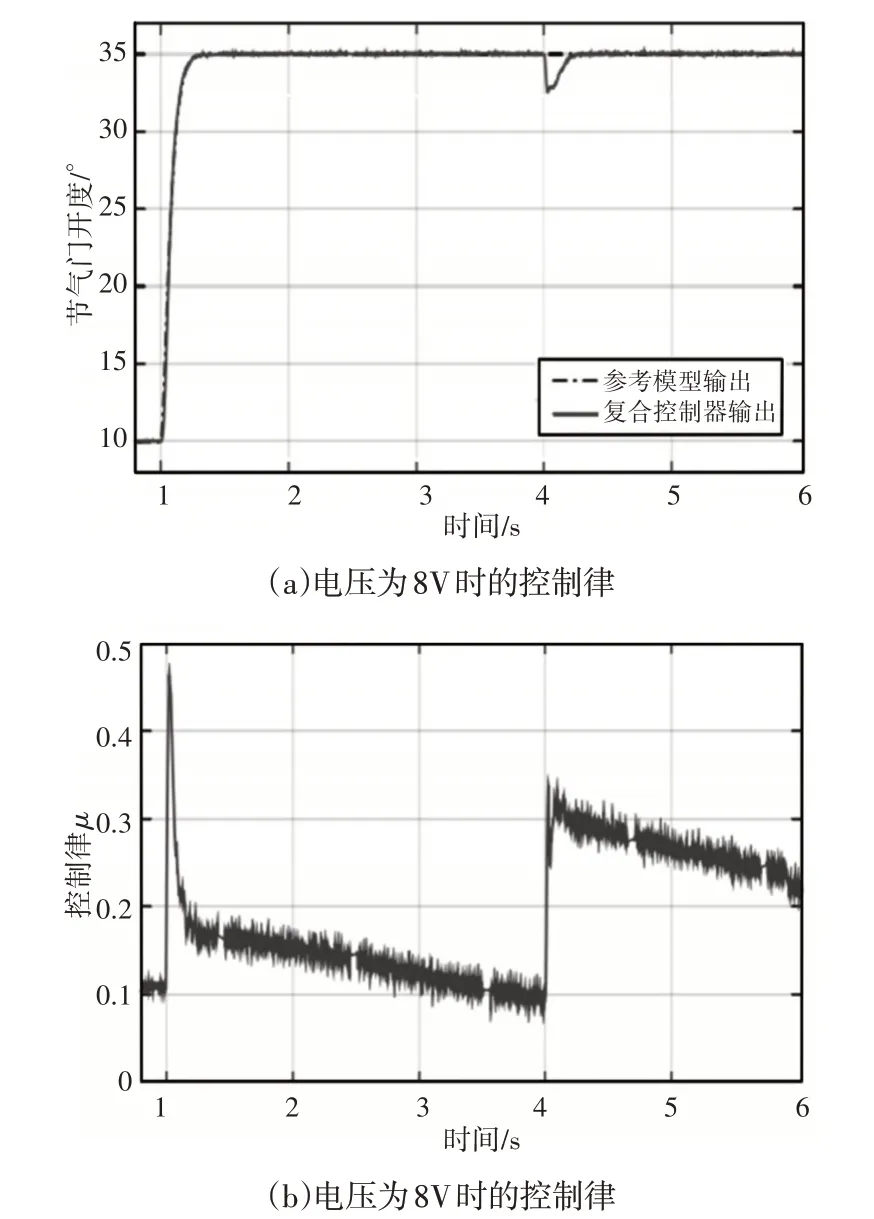
图10 电压为8V时的控制Fig.10 Control Effect When Velocity is 8V

结合图9、图10 的控制效果可知，在模型失配的情况下，复合控制器也能够快速精确跟踪参考输出。另外，在4s时突然施加扰动量，复合控制器的跟踪出现瞬时误差，而后跟踪误差快速减小，迅速跟踪参考输出。这是因为扰动观测器能够实时估计外界扰动和系统内参数不确定性，实现对参考输出的精确跟踪。另外，对比图9（b）、图10（b）的控制律可知，电压为8V时的控制律幅值更大，这是因为模型失配时，集总扰动更大，因此自适应控制律相应增大。综上所述，在存在扰动和参数不确定性情况下，复合控制器能够精确控制节气门开度，系统具有较强的鲁棒性。