电动汽车电驱动桥啸叫特性识别与研究
2023-02-27黄月芹黄显淞李春楠
黄月芹,黄显淞,李春楠
(1.柳州工学院机械工程学院,广西 柳州 545616;2.上汽通用五菱汽车股份有限公司,广西 柳州 545007;3.中汽研(天津)汽车工程研究院有限公司,天津 300300)
1 引言
常见的纯电动汽车电驱动桥由电机、逆变器和单级减速器三个部分构成。对于电驱动桥中电机选择,目前永磁同步电机最为常见,但由于扁线电机槽满率高、功率密度大,将会成为未来电机的主要选择;对于逆变器,其功能是通过控制电流的开关来控制电机策略;对于啸叫阶次最多的减速器,单档减速器是目前的主要选择,两档和多档减速器是未来电驱动桥的发展趋势。
由于纯电动汽车无发动机结构,驱动电机取代内燃机致使传统燃油汽车中的“掩蔽效应”消失,使得电驱动桥内部齿轮副传递误差以及电机电磁力激励产生的啸叫噪声尤为明显,长时间在高频噪声中行驶,会使车内乘员感到烦躁,影响到客户的购买欲望[1]。所以针对电驱动桥的啸叫特征的研究便成为了纯电动汽车NVH性能提升与发展的必经之路。
电机转子在旋转过程中转速的变化会使频谱图上转速的频率分量变得模糊,频谱图上的基频以及其各次谐波分量的功率会分散在一连串的频率谱线上,这种被模糊了的转速频率分量将使其幅值测量造成误差,使得传统的频谱分析难以获得有效效果。传统的分析手段已不能满足变转速下电驱动桥啸叫特征阶次及其边频带的识别精度。短时傅立叶变换的时频分辨率受Heisen‐berg测不准原理的约束,一旦窗函数选定,时频分辨率便确定下来,这使它对分析充满复杂阶次特征的时变信号存在识别精度不高的局限性。Wigner-Ville 分布由于算法本身的原因会产生严重的交叉项干扰,干扰甚至掩蔽信号阶次信息,增加阶次特征识别的困难。
这里针对某型纯电动汽车电驱动桥进行台架试验测试与分析,对其匀加速工况下存在的啸叫问题进行研究,使用阶次分析算法来处理时变转速信号,提高了识别精度,降低了识别难度。
2 阶次分析理论
在信号分析与处理中,假如能使等时间采样转化为等角度采样,那么这时分析显示的转速频率及其各次谐波在频谱图上的位置得以确定,模糊的现象就可以消失,各次谐波分量就可以清楚的被区分开来,这就是阶次分析方法。阶次分析法是由potter[2]首先提出来的,阶次分析是对产生谐波振动的旋转机械进行分析的有效方法之一。实现阶次分析一般有两种方法,即重采样阶次分析和Gbaor阶次分析,但Gbaor变换时窗宽度固定,难以获得高频和低频都理想的分析。因此,这里采样重采样阶次分析来处理时变信号,实现方法是将时域信号通过线性插值转化为角域信号[3-4],再通过加一维窗函数和傅里叶变换得到阶次谱,实现等时间采样到等角度采样的转换。重采样阶次分析的原理流程图和实施方法,如图1所示。
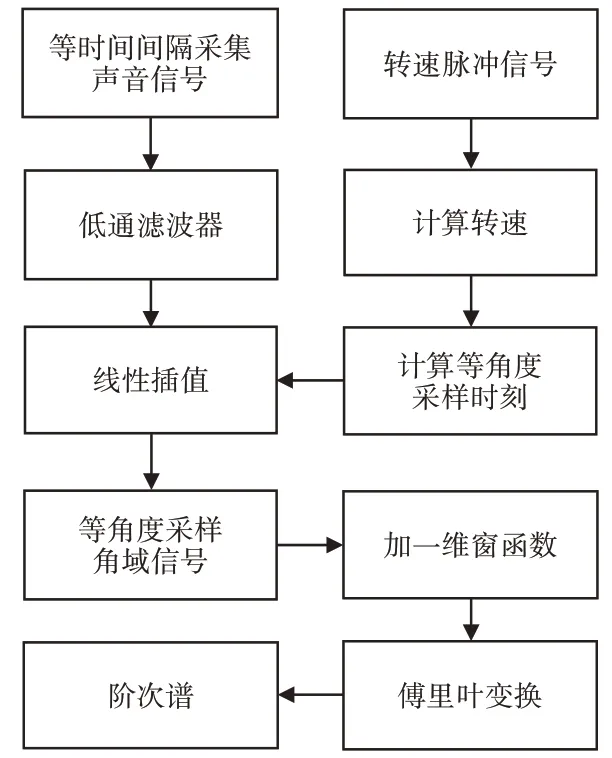
图1 阶次分析步骤Fig.1 Order Analysis Steps
3 电驱动桥啸叫阶次特征分析
3.1 电机特征阶次分析
电驱动桥的电机为8极48槽整数槽的永磁同步电机。由于定子槽的原因,槽附近的气隙磁场会发生局部变化,但是对1阶径向力的影响很小[5-6]。定转子之间狭小的气隙空间会产生周期电磁力,它的径向力波会导致定转子发生可逆的径向变形以及周期性的振动,从而发出具有特定阶次的啸叫噪声。永磁体周围发生的周期性磁场可以用公式表示为:
电枢反应磁场可表示为:
对于整数槽永磁电机v=6k± 1,如果左边等式右侧±为正号时式(2)中ω前面为负号,如果左边等式右侧±为负号时式(2)中ω前面为正号。
根据麦克斯韦应力张量方程,径向电磁力可用公式表示为:
式中:p—定转子极对数;θ—定转子圆周分割的机械角度;ω—电流角频率;μ0—真空磁导率;r—力波阶数;Ar∙μ—第r阶力波相对应的幅值;ωr∙μ—第r阶力波相对应的角频率;ϕr∙μ—第r阶力波相对应的相位。
由式(1)~式(3)可知,48槽永磁电机的最低力波阶数为2p,并且电枢反应磁场的电磁力要小于永磁体磁场的20%[7],所以最低阶径向力主要由永磁体产生的基础磁场发出。
计算得到的电机特征阶次,如表1所示。在变转速下,永磁电机特征频率随着旋转速度的提高而向高频移动,但特征阶次却是一个固定值。

表1 电机阶次Tab.1 Motor Order
3.2 减速器特征阶次分析
电驱动桥内部布置采用单档减速器,由档位齿轮副和主减齿轮副两对组成。减速器齿轮啮合时,齿轮所受负载随着齿轮的转动呈现周期性改变,齿轮副的刚度也随之发生规律性改变,引起齿轮副各个轮齿间的冲击振动。再加上轮齿弹性、变形误差以及轮齿故障等因素影响,都会使齿轮轮齿与轮齿之间发生冲击。因此,在傅里叶频谱图上能够清晰地看到齿轮组的啮合频率及其倍频成分。
电驱动桥内部轴受安装误差以及加工误差等因素的影响,会带动齿轮产生周期性的振动。在频谱中出现啮合频率被各个轴转频调制的边频带。从信号处理以及数学分析认为,幅值调制的基本原理是两路信号在时域上进行乘法运算,在频域上进行卷积运算。在减速器试验采集到的噪声信号当中,载波信号正常情况下包含齿轮对啮合频率,调制信号成分为所在轴的旋转频率。因此,减速器内部齿轮啮合频率为:
式中:fd—挡位齿轮啮合频率;ff—主减齿轮啮合频率;fi—减速器输入轴旋转频率;fm—中间轴旋转频率;fo—输出轴旋转频率;Zdz—减速器挡位主动轮齿数;Zdc—减速器挡位从动轮齿数;Zfz—减速器主减齿轮组主动轮齿数;Zfc—减速器主减齿轮组从动轮齿数。
计算得到的减速器啮合频率以及周围边频带阶次数值,如表2所示。在变转速下,减速器啮合频率及其边频带频率随着旋转速度的升高而增大,但是阶次特征值保持不变。各个轴的转频阶次值,如表3所示。

表2 减速器阶次Tab.2 Order of Reducer

表3 传动轴转频阶次Tab.3 Rotation Frequency Order of Drive Shaft
3.3 滚动轴承特征阶次分析
滚动轴承常见于各种旋转机械结构的内部,起到支撑固定旋转轴的作用。旋转机械结构中30%的故障是由滚动轴承产生的一系列故障导致的[8],当滚动轴承出现故障时,非平稳信号占据故障信号的绝大部分[9],所以对试验信号中滚动轴承的特征阶次研究就成为了改善电驱动桥NVH性能的有效途径。
传动轴在旋转过程中带动滚动轴承内圈旋转以及轴承滚珠自转和公转,滚动轴承内部结构,如图2所示。由于传动轴在旋转过程中存在动不平衡量,导致旋转到不同角度承载的滚子数目不同,如图3所示。当轴承承载刚度发生周期性变化时,会引起滚动轴承内圈的轴心位置变化,从而产生滚动体的传输振动,振动的主要频率为fcZ[10]。
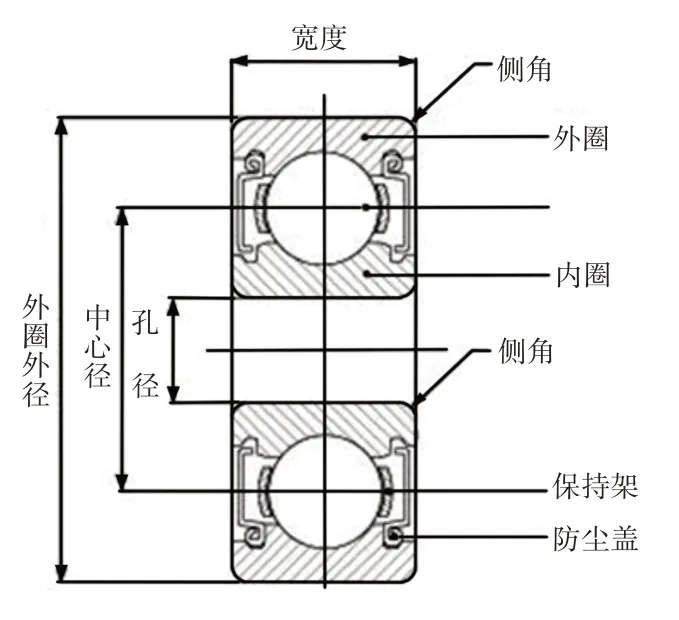
图2 滚动轴承内部结构Fig.2 Internal Structure of Rolling Bearing
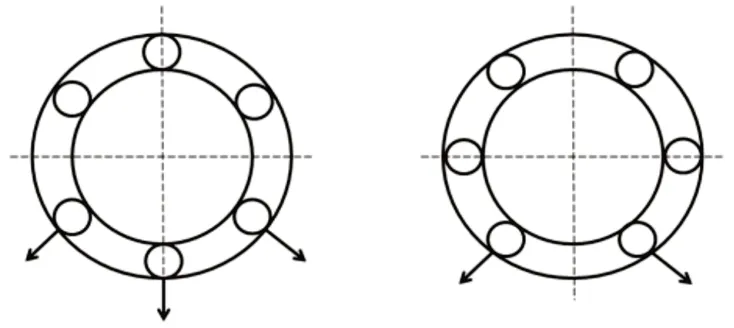
图3 承载滚动体数目不同Fig.3 The Number of Loaded Rolling Elements is Different
传动轴在自转旋转时受到齿轮重力以及动不平衡量的惯性影响发生弯曲,轴承内圈以及滚珠发生微小的位置周期性变化,其周期性变化的频率为fcZ±fr。
式中:Z—滚动体的个数;fc—滚动体围绕传动轴的公转频率;fr—所在轴的旋转频率;d—滚珠直径;D—轴承中心径;α—旋转角度。
滚动轴承的特征阶次,如表4 所示。电驱动桥轴承位置简图,如图4所示。
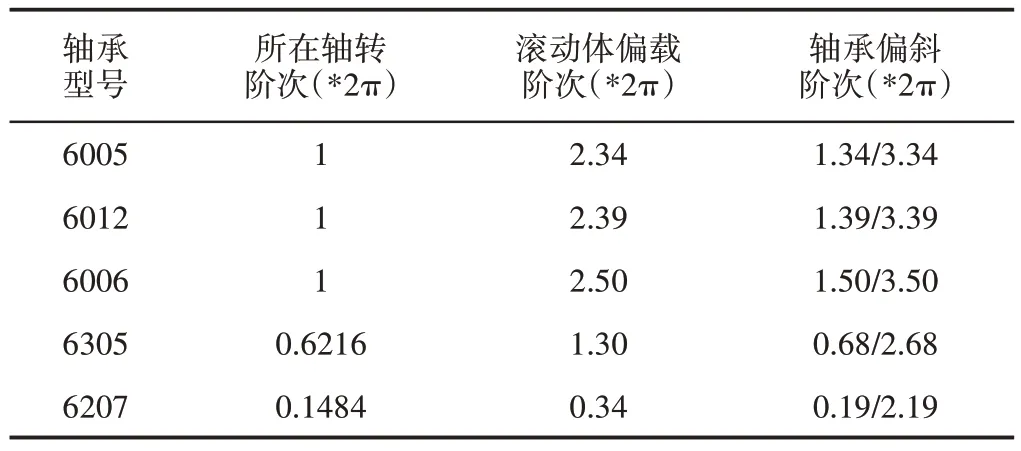
表4 滚动轴承特征阶次Tab.4 Rolling Bearing Characteristic Order
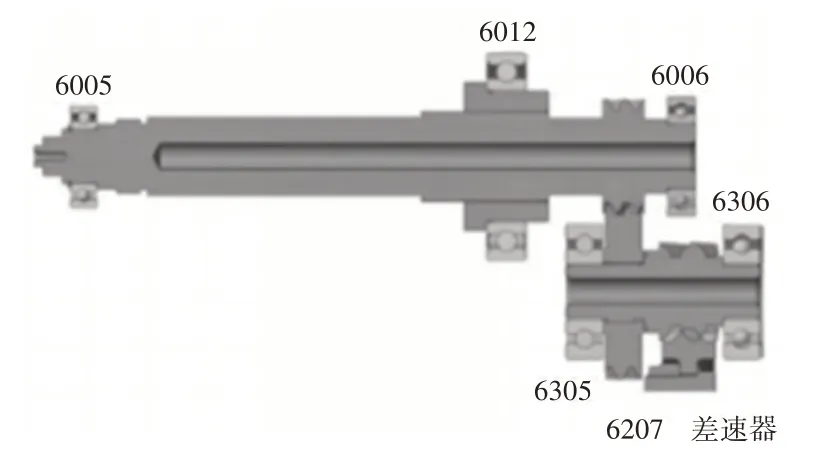
图4 电驱动桥轴承位置Fig.4 Electric Drive Axle Bearing Position
4 试验与分析
噪声信号的采集是电驱动桥特征阶次识别的首要步骤,要体现阶次分析的优势必须采集到转速稳定上升且工况合理的一维离散声压信号。根据测试试验经验以及总成级噪声测试标准,我们可以得到台架试验的测试方案以及数据采集的基本参数设置,为下一步的噪声信号阶次分析做好充足的试验准备。
4.1 台架试验
噪声测试的对象为某企业生产的电驱动桥,台架试验测点布置的三维图,如图5所示。电驱动桥的输出端搭载两台负载测功机,通过悬置与工装基座相连固定,整个台架试验无声学包裹。电驱动桥使用此工装方案模拟在实际样车上的安装方式,安装到测功机上,且工装模态>800Hz。噪声远场测点布置采用五点法,即距离电驱动桥壳体表面1m的前、后、左、右、上五个方向上的五点,采集驱动桥的远场噪声。为了研究电驱动桥的啸叫噪声,试验采用瞬态加速工况,永磁电机的转子转速从1000r/min匀加速上升至6000r/min,永磁电机的输出扭矩为55Nm。电驱动桥外场噪声信号采集过程如下:先通过永磁电机控制器将旋转速度稳定在1000r/min,然后匀加速上升至6000r/min。最后通过LMS公司的数采系统收集加速工况下的时域噪声信号及转速信号。
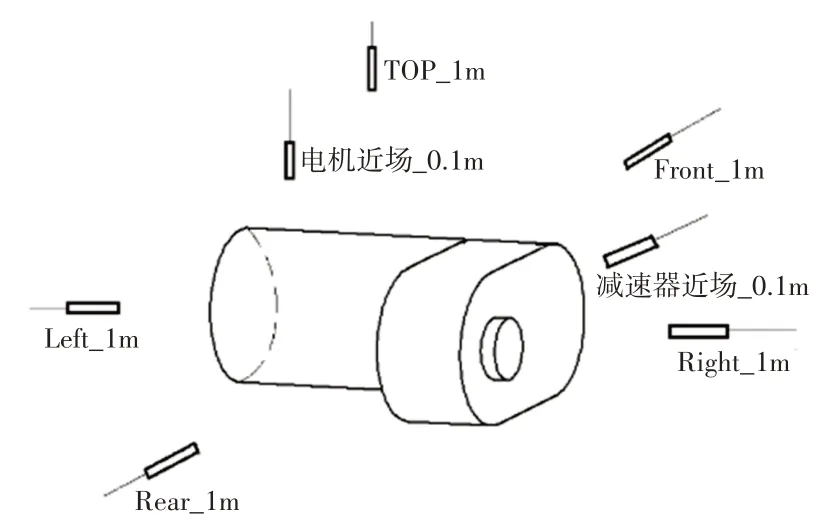
图5 台架试验测点布置示意图Fig.5 Schematic Diagram of the Layout of Test Points
4.2 数据分析
对采集到的顶部1m 远场加速噪声信号采取短时傅里叶变换,如图6 所示。减速器齿轮的啮合阶次以及电机的定子槽特征阶次较为明显,由于短时傅里叶变换本身存在的分辨率缺陷,无法在图中找到电机的转子极对数特征阶次以及连续清晰可见的电驱动桥特征阶次倍频。低频率局部放大图,如图7 所示。只能在图中发现非连续的输入轴转频阶次及其倍频,所以使用传统的FFT并不能看到连续清晰的电驱动桥特征阶次及其倍频,也不会看到某些只在特定转速和频率才能突显出来的早期故障阶次。
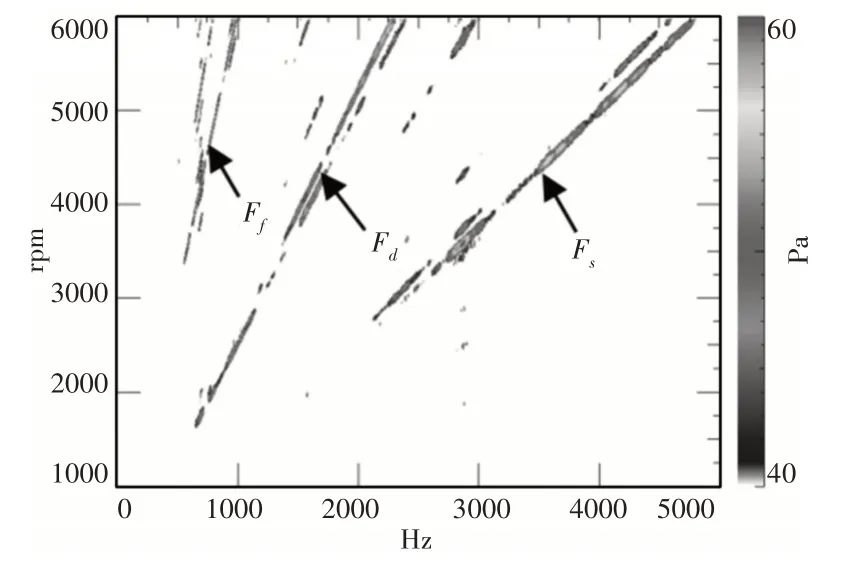
图6 1m噪声短时傅里叶变换Fig.6 1m Noise Short-Time Fourier Transform
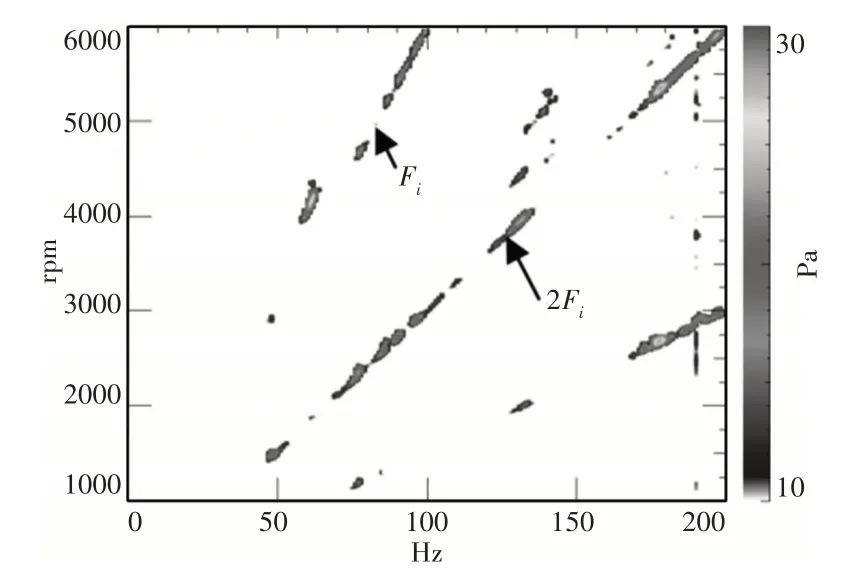
图7 低频局部放大Fig.7 Local Amplification of Low Frequency
阶次分析是将时域信号转变成角域信号再进行傅里叶变换的信号处理方法,能完美解决上述阶次特征线不连续或者不明显的问题。针对上述工况下收集到的噪声信号和转速信号采取阶次分析的方法,如图8所示。减速器内部齿轮对的啮合阶次、周围的倍频成分以及电机的特征阶次较为明显,低阶次局部放大图,如图9所示。能发现较为突出的输入轴和输出轴转频阶次,无轴承特征阶次,说明轴承受力均匀无故障。减速器档位齿轮啮合阶次附近放大图,如图10所示。可以清晰地发现档位齿轮啮合阶次被三个轴转频阶次调制的边频带,说明在匀加速工况下三个轴都存在不对中的现象。
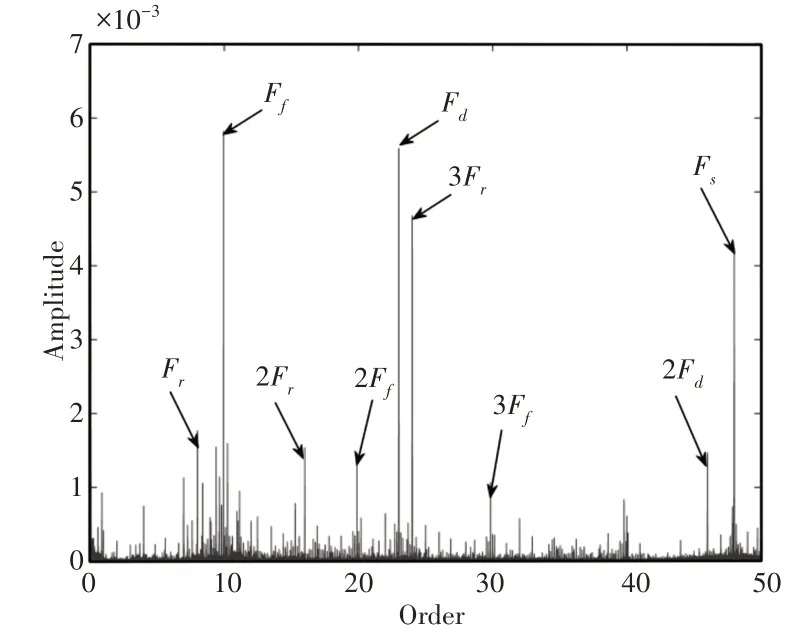
图8 阶次分析Fig.8 Order Analysis
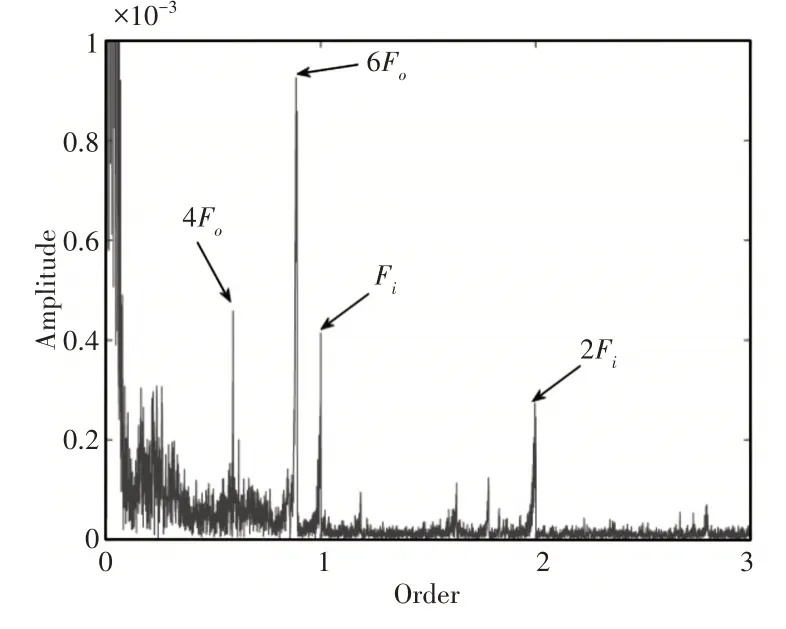
图9 低阶次局部放大Fig.9 Low-Order Partial Enlargement
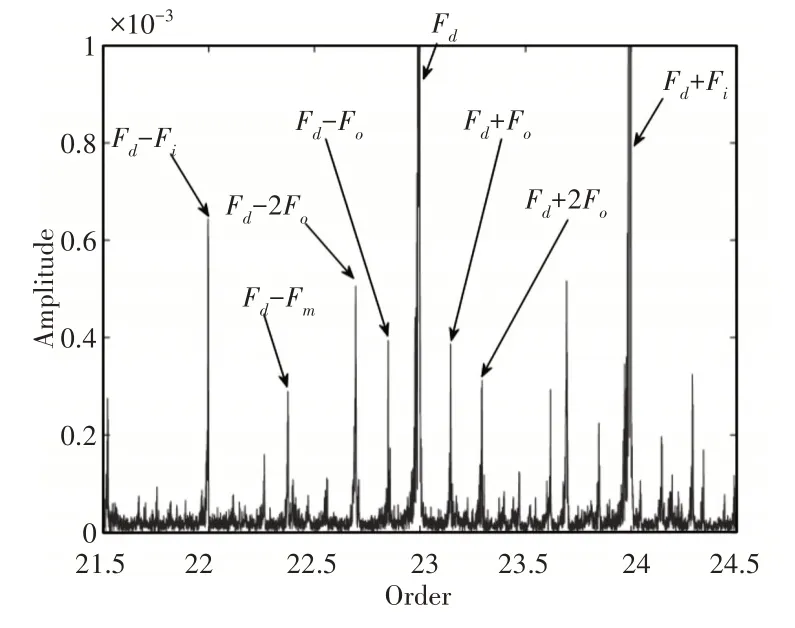
图10 档位齿轮啮合阶次局部放大Fig.10 Partial Enlargement of Gear Meshing Order
根据上述两种不同信号处理方法的区别,将阶次分析的优点归为下列三点:
(1)只突出信号的阶次特性,降低底噪的影响;
(2)有较好的阶次分辨率;
(3)各阶次噪声幅值对比明显。
5 结论
加速工况下,电磁力的径向力会使电驱动桥内部的定转子产生形变从而出现周期性的振动噪声,阶次特征值为永磁电机的极对数和定子槽个数;电驱动桥内传动轴存在不对中的现象,使减速器齿轮啮合阶次附近存在被三个轴转频阶次调制的边频带。相比较于传统的时频分析方法,阶次分析的阶次分辨率高,底噪低,适用于提取电驱动桥的特征阶次以及问题阶次,也适用于电驱动桥的早期故障特征识别。
