Novel Distance Measures on Hesitant Fuzzy Sets Based on Equal-Probability Transformation and Their Application in Decision Making on Intersection Traffic Control

Fangwei Zhang,Yi Zhao,Jun Ye,Shuhong Wang and Jingyi Hu

1Naval Architecture and Port Engineering College,Shandong Jiaotong University,Weihai,264209,China

2College of Transport and Communications,Shanghai Maritime University,Shanghai,201306,China

3College of Automotive and Traffic Engineering,Nanjing Forestry University,Nanjing,210037,China

4School of Civil and Environmental Engineering,Ningbo University,Ningbo,315211,China

5School of Business,National University of Singapore,118414,Singapore

6Durham Law School,Durham University,Durham,DH1 3LE,UK

ABSTRACT The purpose of this study is to reduce the uncertainty in the calculation process on hesitant fuzzy sets (HFSs).The innovation of this study is to unify the cardinal numbers of hesitant fuzzy elements(HFEs)in a special way.Firstly,a probability density function is assigned for any given HFE.Thereafter,equal-probability transformation is introduced to transform HFEs with different cardinal numbers on the condition into the same probability density function.The characteristic of this transformation is that the higher the consistency of the membership degrees in HFEs,the higher the credibility of the mentioned membership degrees is,then,the bigger the probability density values for them are.According to this transformation technique,a set of novel distance measures on HFSs is provided.Finally,an illustrative example of intersection traffic control is introduced to show the usefulness of the given distance measures.The example also shows that this study is a good complement to operation theories on HFSs.

KEYWORDS Hesitant fuzzy sets;equal-probability mapping;distance measure;intersection traffic control;cardinality theory

1 Introduction

As an important tool of group decision making,hesitant fuzzy set(HFS)assigns the membership degree of an element to a set with a set of possible values [0,1] ([1–5]).Distance is a fundamental feature in describing the relationship between HFSs.It is well known that when the distance of different hesitant fuzzy elements(HFEs)are calculated,their cardinalities should be unified firstly([6–9]).How to realize it? The classical models usually extend the shorter HFE until they have the same cardinal number.Usually,the shorter HFE is extended by putting more minimum value,maximum value,or any value in it with the existing ones.Actually,many values empirically exist in the shorter HFE.Thus,it is very necessary to improve the classical distance measures on HFSs by using some novel techniques to unify the cardinal numbers of the calculated HFEs.In this study,the cardinality problem is considered in another way,where equal-probability mapping,cardinality,and impulse function are combined to define a kind of novel distance measures for HFSs.Based on the new proposed distance measures,any two HFSs with different cardinal numbers can be dealt with as the same in the case that they have the same number of elements.Such a theory is feasible from the point of probability([10–12]),and some classical studies on the combination of probability theory and hesitation fuzzy sets please refer to Liu et al.[13],Liu et al.[14],etc.Meanwhile,since this kind of technique is of multi-source heterogeneous data,it can also be used in intuitionistic fuzzy sets(IFSs).For example,Mahmood et al.[15]divided the information on IFSs and HFSs into different grades,and proposed a novel algorithm to integrate this information.Similarly,the research results of this study can be extended to the field of IFSs too.

The characteristic of the newly proposed method is to make full use of the existing decision making information,and not to add artificial one,so as to keep the objectivity of decision making process.The technique adopted in the proposed method is equal probability transformation,which guarantees the constant probability of the theoretical truth value appearing at each point before and after the transformation.Besides,this technique is also suitable to be used in aggregation operators on HFSs.For more details on this issue,please refer to Xia et al.[16].To describe the idea clearly,the remainder of this study is arranged as follows.Section 2 introduces some basic concepts on HFSs,and introduces a series of classical distance measures.Section 3 introduces the concept of equalprobability transformation on HFSs,gives three properties of the transformation,and proposes a series of improved distance measures.Section 4 introduces a traffic control mode decision making problem,and solves it by the proposed improved distance measures on HFSs.Finally,the main innovation points are concluded in Section 5.

2 Preliminaries

In this section,some basic definitions and some classical distance measures on HFSs are reviewed.For convenience’s sakeX={x1,x2,...,xn},is denoted as the discourse set throughout this study.

Definition 1(Torra[2])Let X be a given set,an HFS E on X is demonstrated as a function that when applied to X returns a subset of[0,1],which can be described asE={〈x,hE(x)〉|x∈X},wherehE(x)is a set of values in[0,1],representing the possible membership degrees of the elementxto the HFS E.For convenience,hE(x)is called an HFE.The classical definition of distance measure on HFSs was addressed by Xu et al.[4]as follows.

Definition 2(Xu et al.[4])Let M and N be two HFSs on X,then the distance measure on M and N is described asd(M,N),which satisfies the following three properties,i.e.,(i)0≤d(M,N)≤1,if and only ifM=N;(ii)d(M,N)=d(N,M).By referring to Hamming distance and the Euclidean distance,Xu et al.(2011)defined.

Definition 3(Xu et al.[4]) Let M and N be two HFSs on X.For anyxi∈X(1≤i≤n),letl(hM(xi))andl(hN(xi))be the cardinal numbers ofhM(xi)andhN(xi),respectively.Then,the hesitant normalized Hamming distance,Euclidean distance and generalized hesitant normalized distance are proposed as

wherelxi=max{l(hM(xi)),l(hN(xi))},λ>0,(xi)and(xi)are thejth largest values inhM(xi)andhN(xi),respectively.It is noteworthy thatl(hM(xi))/=l(hN(xi)) holds in most cases,to operate them correctly,one should extend the shorter one until the cardinal numbers ofhM(xi)andhN(xi)are the same.

Definition 4(Xu et al.[4]) LetMandNbe two HFSs onX,if one takes the weightwi(i=1,2,...,n)of each elementxi∈Xinto account,the generalized hesitant weighted distance is proposed as

where λ>0.

3 Main Results

In classical calculation process on HFSs,to satisfy Eqs.(1)–(4),part of the information on HFSs has to be artificially added when the cardinality of HFEs is different.In an environment characterized by uncertainty,this process further increases the uncertainty of computing problems and weakens support for decision-makers.To reduce the uncertainty in the calculation for HFSs,for any given HFEh1with any given cardinal numberi(i∈N),the task of this study is to transferh1to a new HFEh2with cardinal number j for any givenj(j∈N),whereh1andh2are the same in statistics.Generally speaking,this transformation consists of two parts.Firstly,a probability density function for HFE is proposed.Secondly,an equal-probability transformation function is given.

3.1 Probability Density Function for HFE

From the viewpoint of probability,the truth value of membership function of any given HFE can appear at any point between the smallest and the largest occurred membership degree,but the probability of occurrence is different for different values.Logically,the probability that a certain point is the true value of membership degree of HFE is related to the occurred value of membership degree near this point.When the occurred value of membership degree function is far away from the point,it is thought that the probability of the true value in this point is low;otherwise,the probability is high.Guided by this idea,a probability density function for HFE is introduced as follows.

Definition 5Suppose that there is an HFEh={h1,h2,...,hm},and suppose thath1≤h2≤···≤hm.Then,a probability density function for h is given as

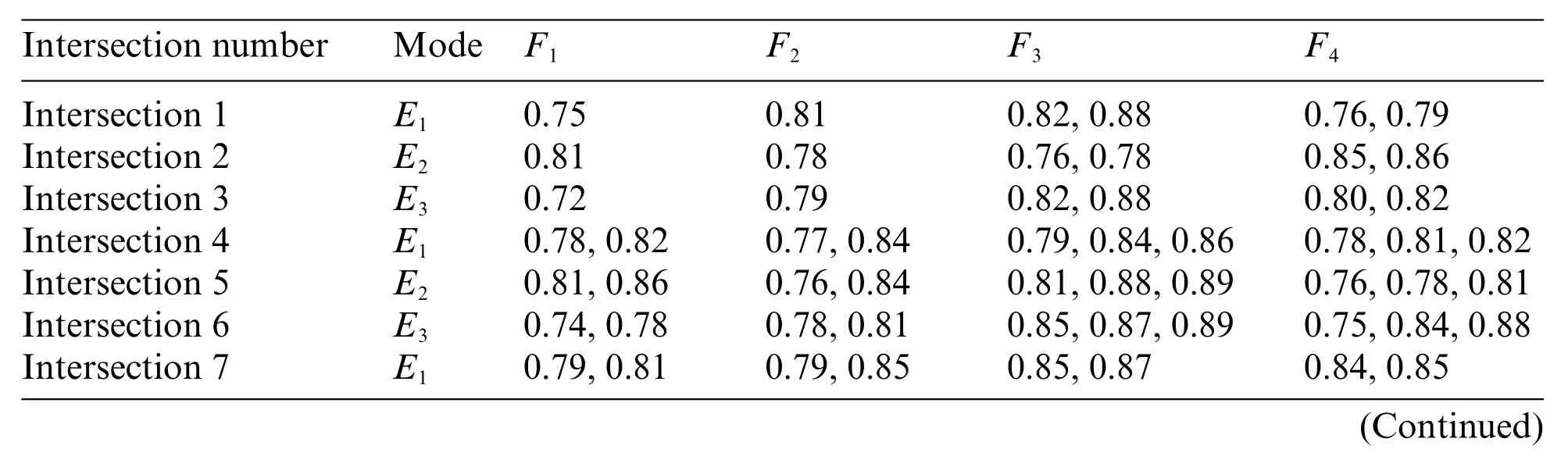
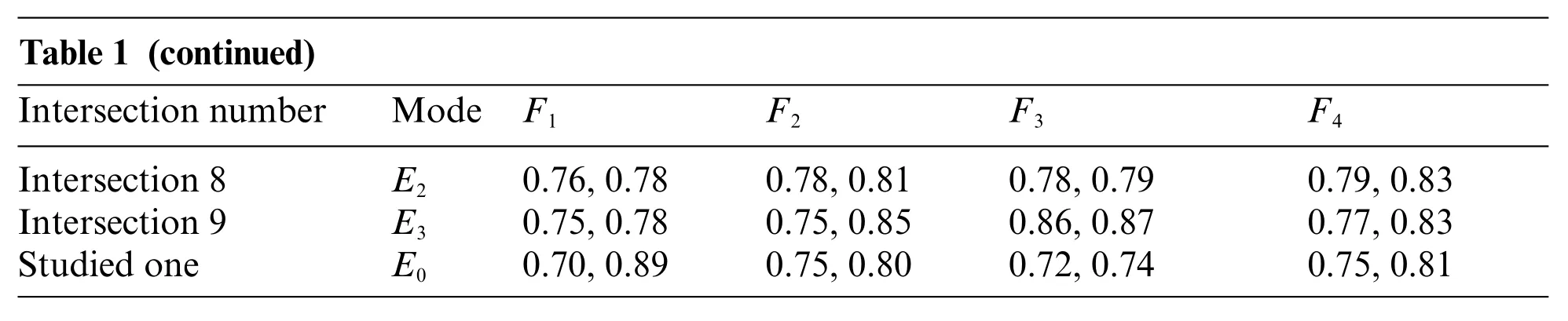
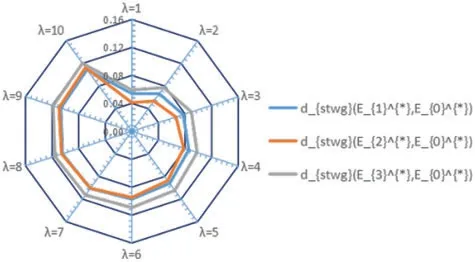
where 0<ε

On the probability density function for HFSs,some properties are summarized as follows.

Property 1By Eq.(5),for any given HFEh,there is only one probability density functionwhich corresponds to it.

Property 2If any given HFE h and its probability density functionfor any interval[hi,hi+1] in the definition domain ofthe smaller is the valuehi+1−hi,the bigger the value ofis.

Property 3If any given HFEhand its probability density functionfor any duplicate elementshiinh,there is an impulse functionP(hi) inThe more able ishi,the stronger the impulse function is.

3.2 Equal-Probability Function and Their Properties

For any given HFE,the occurrence interval of the true value of its membership degree can be calculated by Eq.(5).On the premise of keeping the probability density function of true value at any point in the interval unchanged,the expression form of HFE can be changed by specific skills.Specifically,the equal-probability function for HFSs is proposed in this subsection.

Definition 6Suppose that there is an HFEh={h1,h2,...,hm},whereh1≤h2≤···≤hm.Suppose the probability density function forhis given asThen,the seth′=is defined as the equal-probability mapping ofhtoh′,whereh′1=h1,h′n=hm,and for anyj∈{1,2,...,n−1},it holds that

By using Definition 6,an HFE is transferred to another new HFE under the condition that the two variables share the same probability distribution function.An important property on equal-probability function for HFSs is introduced as follows.

Property 4Suppose that there are two HFEsh={h1,h2,...,hm}andh′=whereh1≤h2≤···≤hm,h′1≤h′2≤···≤h′n.Suppose thatDenoteThen,it holds that

ProofBy Eq.(5),it gets thatSinceit getsFor anyi∈ {1,2,...,m},j∈ {1,2,...,n},by Eq.(6),it gets thatTherefore,it gets that

To illustrate Definition 6 clearly,a case is given as follows.

Case 1Suppose that there is an HFEh∗={0.25,0.35,0.35,0.45}.Please calculate the probability density functionand transfer h∗to a new HFEh∗∗with cardinal number 6,where

Firstly,the probability density function forh∗is obtained by Eq.(5),which is denoted as

Therefore,it getsh∗∗={0.25,0.31,0.35,0.35,0.39,0.45}.Obviously,it holds

By further study,Def.7 is obtained in the following.

Definition 7Suppose that there are K HFSsh1,h2,...,hKonX={x1,x2,...,xN},and for anyxi∈X(1≤i≤N),the set of membership values of xi tohk(1≤k≤K) is defined ashk(xi)=wherel(hk(xi)) is the cardinal number ofhk(xi) for anyk∈{1,2,...,K}.Rank the elements ofhk(xi) by monotone increasing order,and denote the ranking result asDenoteN′(xi)=max{l(hk(xi))}(1

Definition 8Suppose that there areKHFSsh1,h2,...,hKonX∈{x1,x2,...,xN}.For any(xi),divides the intervalintoN′(xi)−1 sub-intervals,and denote its corresponding set of segmentation points aswhere(xi)equals(xi),and(xi)satisfiesdx=(N∗−1)−1.It is noteworthy that there is a possibility that there are some(xi)and(xi)are equal.By

Knew sets(xi)(k=1,2,...,K) are constructed.For anyk∈ {1,2,...,K},rank all the elements of(xi) in monotonically increasing order,anddenote the result ash∗k(xi)={h∗k(x1),h∗k(x2),...,h∗k(xN)},whereh∗k(xi)=

3.3 Improved Distance Measures on HFSs

By using equal-probability equations,a series of improved distance measures on HFSs are obtained as follows.

Definition 9Suppose that there areKHFSsh1,h2,...,hKonX={x1,x2,...,xN}.For anyk1,k2∈{1,2,...,K},the improved hesitant normalized Hamming distance,Euclidean distance and generalized hesitant normalized distance betweenhk1andhk2onXare proposed as

where λ>0,(xi)and(xi)are thejth ordinal values in(xi)and(xi),respectively.

Definition 10When one takes the weightwiof each elementxi∈Xinto account,a generalized hesitant weighted distance is obtained as

Analogously,for anyx∈X,the distance between two HFEshk1(x)andhk2(x)is defined as

where λ>0,(x)and(x)are thejth ordinal values in(x)and(x),respectively.

In terms of cardinality,Eqs.(9)–(15)are consistent with Eqs.(1)–(4).To illustrate the performance of the proposed distance measures,an example is given in the following section.

4 Illustrative Examples

4.1 Problem Introduction

At present,the at-grade intersection is an important kind of complex node in urban road.In traffic engineering fields,there are three basic methods of traffic control which could be implemented at an intersection,i.e.,“method 1-uncontrolled intersection”;“method 2-intersection with right assignment using Yield or Stop signs”;and“method 3-signalized intersection”[17].For the sake of understanding,these three kinds of traffic control modes are illustrated by the picture(Figs.1–3),respectively.

Figure 1: Method 1 traffic control

Figure 2: Method 2 traffic control

Figure 3: Method 3 traffic control

In China,the most frequently used traffic control modes at intersections are “roundabout control”,“Yield or Stop signs control”,and “traffic signal control”,where they also belong to the above three control methods,respectively [18].For the sake of convenience,these three kinds of control models are denoted byE1,E2,E3.To select a suitable type of control mode for an intersection,traffic engineers usually consider many factors which include“the grades of the intersection”,“traffic flow volumes”,“saturation degrees (the ratio of traffic demand to traffic capacity) of the entrance lanes”,and “geographical position of the intersection in the city”.Here,the aforementioned four kinds of factors are denoted byf1,f2,f3andf4.Suppose in Pudong District,Shanghai City,China,an intersection E0needs to be designed and constructed.Suppose that the traffic control modesE1,E2,E3all satisfy existing government standards(Ministry of Housing and Urban-Rural Development of the People’s Republic of China [19]; Ministry of Construction of the People’s Republic of China [20];Ministry of Housing and Urban-Rural Development of the People’s Republic of China [21]).Then,the novel proposed decision making method is used to determine the intersection’s traffic control mode [22].To choose the suitable control method,nine INTs in Pudong district,Shanghai city are investigated which are all in good traffic control effects and they contain all the three traffic control modesE1,E2,E3.Denote F1 as the fuzzy set“the highway grade”where the better the functions of the intersection,the larger is the membership degreeF1;denoteF2as the fuzzy set“traffic flow volume”;denoteF3as the fuzzy set “saturation degree of the traffic flow”; and denoteF4as the fuzzy set“geographical position”where the nearer the distance between the related intersection and the city center is,the larger is the membership degree of the intersection toF4.Then,the membership degree of each intersection to each attribute is obtained in Table 1.

Table 1: The membership degree of each intersection to each fuzzy set

Table 1 (continued)Intersection numberMode F1F2F3F4 Intersection 8E20.76,0.780.78,0.810.78,0.790.79,0.83 Intersection 9E30.75,0.780.75,0.850.86,0.870.77,0.83 Studied oneE00.70,0.890.75,0.800.72,0.740.75,0.81

By information aggregation,E1,E2,E3are expressed asE1={hE1(F1),hE1(F2),hE1(F3),hE1(F4)},E2={hE2(F1),hE2(F2),hE2(F3),hE2(F4)},E3={hE3(F1),hE3(F2),hE3(F3),hE3(F4)},wherehE1(F1)={0.75,0.78,0.82,0.79,0.81},hE2(F1)={0.81,0.86,0.81,0.78,0.76},

hE3(F1)={0.72,0.74,0.78,0.78,0.75},hE1(F2)={0.81,0.84,0.77,0.79,0.85},

hE2(F2)={0.78,0.76,0.84,0.78,0.81},hE3(F2)={0.79,0.78,0.81,0.85,0.75},

hE1(F3)={0.82,0.88,0.84,0.79,0.86,0.85,0.87},hE2(F3)={0.78,0.76,0.81,0.88,0.89,0.79,0.78},

hE3(F3)={0.88,0.82,0.89,0.85,0.87,0.87,0.86},hE1(F4)={0.76,0.79,0.78,0.81,0.82,0.84,0.85},

hE2(F4)={0.85,0.86,0.81,0.78,0.76,0.79,0.83},hE3(F4)={0.80,0.82,0.84,0.88,0.75,0.77,0.83}.

Similarly,the studied intersection could be expressed as a hesitant fuzzy setE0={〈F1,{0.70,0.89}〉},{〈F2,{0.75,0.80}〉},{〈F3,{0.72,0.74}〉},{〈F4,{0.75,0.81}〉}.Moreover,the weight vector forf1,f2,f3,f4is known asWT=(0.30,0.25,0.25,0.20).

4.2 Decision Making Process

In this subsection,the decision making problem is solved by using the novel distance measures.Firstly,sort the elements of each(i=1,2,3;j=1,2,3,4) by using ascending counts,and denote the calculation results as(F1)=(0.75,0.78,0.79,0.81,0.82),(F1)=(0.76,0.78,0.81,0.81,0.86),(F2)=(0.77,0.79,0.81,0.84,0.85),(F2)=(0.76,0.78,0.78,0.81,0.84),(F2)=(0.75,0.78,0.79,0.81,0.85),(F3)=(0.79,0.82,0.84,0.85,0.86,0.87,0.88),(F3)=(0.76,0.78,0.78,0.79,0.81,0.88,0.89),(F3)=(0.82,0.85,0.86,0.87,0.87,0.88,0.89),(F4)=(0.76,0.78,0.79,0.81,0.82,0.84,0.85),(F4)=(0.76,0.78,0.79,0.81,0.83,0.85,0.86),(F4)=(0.75,0.77,0.80,0.82,0.83,0.84,0.88).Next,by the definition ofN∗,N∗=7.SinceN1/=7,N2/=7,N3=7,N4=7,for anyi=1,2,3,remain all the(F3)and(F4)as what it should be,and denote

Thereafter,for every(F1) and(F2),denote their corresponding probability density function as

Then,the intervals corresponding toare[0.75,0.82],[0.76,0.86],[0.72,0.78],[0.77,0.85],[0.76,0.84],[0.75,0.85].Divide them by Eq.(5) in proper sequence,and the seven sets of segmentation points are obtained as

Analogously,E0is transferred towhere

For λ=1,2,...,10,by using Eq.(12),and taking the weights off1,f2,f3andf4into account,three kinds of generalized hesitant weighted distancesare obtained,respectively,which are shown in Fig.4.Besides,for any given λ=1,2,...,10,the differences betweendλ(E1,E0)anddλ(E2,E0)are very small.Thereafter,Fig.5 contrastsE1andE2.

Figure 4:Distances obtained by using d__{stwg}

Figure 5:Contrast map of three kinds of distances

Figs.4 and 5 illustrate that the suitable intersection Traffic Control mode varies as the parameter λ.Specifically,when λ≤7,all the suitable intersection traffic control modes are E2;when λ≥8,all the suitable intersection traffic control modes areE1.The essence of the above conclusions is that the smaller the λ is,the more appreciated the over-all evaluation information of the entire committee of experts is; meanwhile,the larger theλis,the more appreciated the unduly large or small evaluation values of the evaluation information are.Therefore,to issue the intersection traffic control pattern decision making problem,one can firstly select a suitable parameter λ according to specific traffic control circumstances.More details on λ,please refer to Goldberg[23].

4.3 Comparison and Analysis

In this subsection,the given problem can is solved by using classical methods.For example,by using Definition(3)proposed by Xu et al.[4],E0can be transferred aswhere(F1)={0.70,0.89,0.89,0.89,0.89,0.89,0.89},={0.75,0.80,0.80,0.80,0.80,0.80,0.80},={0.72,0.74,0.74,0.74,0.74,0.74,0.74},={0.75,0.81,0.81,0.81,0.81,0.81,0.81}.Similarly,for any giveni=1,2,3,j=1,2,3,4,can also be transferred asSpecifically,it also gets that

Then,for λ=1,2,...,10,by using Eq.(12),and taking the weights off1,f2,f3andf4into account,three kinds of generalized hesitant weighted distancesare obtained,respectively,which are shown in Table 2.

Table 2: Distance between the studied one and each traffic control mode

Table 2 illustrates that the suitable intersection traffic control mode varies as the parameter.Specifically,when λ≤6,all the suitable intersection traffic control modes areE2; when λ≥7,all the suitable intersection traffic control modes areE1.Obviously,the results are generally consistent with those obtained by the novel method.However,there are some slight differences which mainly occur when λ=7.In essence,this is due to the added subjective data when using classical method.The differences show that the newly proposed method is more objective than classical ones in data processing.

5 Conclusion

In calculating the distance between two HFEs with different cardinal numbers,the cardinalities of them should be unified.To reduce the uncertainty in the unifying process,equal-probability transformation is used.Specially,a series of improved distance measures on HFSs are proposed.Since the essence of equal-probability transformation is a kind of dimensional transformation of the same information in the way of expression,the proposed method retains the decision information completely.By contrast,it is difficult to achieve this effect using classical methods.Moreover,the main innovations of this study are concluded as follows:

(i) The theoretical basis of this study is to deal with the membership function value of HFSs from the viewpoint of probability.Moreover,an equal-probability transformation technique is proposed to transform any given HFE into a new one with specified cardinal number.

(ii) To express the enhancement effect for the same membership function value of HFE occurring more than once,impulse function is introduced into hesitant fuzzy fields.This is consistent with people’s production experience.

(iii) This study is a multidisciplinary combination of the theories of the cardinality,equalprobability mapping,and impulse function.

In general,the innovation of this study mainly lies in the unification of multi-source heterogeneous data.This innovation can be applied not only to HFSs,but also to HFSs or NFSs,etc.

Ethical Approval:This article does not contain any studies with human participants performed by any of the authors.

Funding Statement:The Fangwei Zhang’s work is partially supported by Shanghai Pujiang Program(No.2019PJC062),the Natural Science Foundation of Shandong Province(No.ZR2021MG003),the Research Project on Undergraduate Teaching Reform of Higher Education in Shandong Province(No.Z2021046).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.